With the wide application of mechanical products, people have more and more stringent quality requirements, which poses a great challenge for the accuracy of mechanical equipment. However, in actual working conditions, mechanical equipment will produce adverse effects such as vibration, wear, and noise due to the existence of clearance[1-2]. Joint clearance is a key factor to ensure that two connectors have relative position relationship in a small space and relative motion and assembly relationship between parts. The friction at the clearance leads to deformation and damage of parts, which affects machining accuracy and reduces mechanical efficiency. Besides, improper selection of friction coefficient will seriously shorten the service life of equipment[3-6]. Therefore, in mechanism dynamics analysis, influence of joint clearance should be considered urgently.
Parallel mechanism has the advantages of strong bearing capacity, high sensitivity of the end actuator, and high precision over series mechanism. However, due to the excessive branches in parallel mechanism, the researchof dynamics of parallel mechanism is more complex. At present, scholars have made fruitful achievements in the study of dynamic performance of series mechanism. Flores et al.[7] took the space secondary pendulum as the research object, and proved the feasibility that the external forces produced because of clearance should be introduced into system formula. Tian et al.[8] investigated the dynamics characteristics for spatial double pendulum mechanism under the condition that there is clearance between the flexible bar and the joint. Wang and Liu[9] studied the dynamic characteristics of crank-connecting rod mechanism in internal combustion engine under the condition of clearance, and surveyed its motion characteristics at the center of high-speed time clearance. Erkaya et al.[10] established crank slider with spatial structure as the analysis model, and considered its influence on the whole mechanism in the presence with spherical clearance joints. Pratiher[11] analyzed non-linear responses of flexible arm under axial load based on D'Alembert principle, then compared the result obtained by numerical simulation with that by normal form method. Li et al.[12] considered the dynamics responses for a spatial manipulator with clearance under different gravity environments, and designed an ADRC algorithm to improve the control accuracy of the manipulator. Liu et al.[13] studied influences of friction at the rotating joint clearances on dynamic response of manipulator with flexible links, and analyzed the influence of Coulomb friction model and Luger friction model on the spatial manipulator, respectively.
Nowadays, the existing researches on clearance are mainly focused on plane parallel mechanisms with revolute joints. However, there are very few researches on spatial parallel mechanisms with spherical joints. Flores et al.[14] discussed dynamics behavior about crank slider with revolute clearance joints, and obtained the acceleration response curve of slider by MATLAB simulation, which was confirmed by experimental research. Bai and Sun[15] investigated the impact of multiple revolute clearance joints on dynamics characteristics of planar four-bar linkage. Xu et al.[16] analyzed the influence of different clearance values on dynamics responses of planar parallel robot when there are multiple rotational clearances. Varedi-Koulaei et al.[17] studied dynamics response for three-RRR all clearance parallel mechanisms with all clearance under the influence of different driving speeds and clearance values. Zhang and Zhang[18] studied dynamic response for planar redundant drive four-RRR to the system in the presence of clearance, and compared it with the results of experiment and simulation software. Chen et al.[19] proposed a precision prediction method, analyzed the impact of joint clearances on planar 3-RPR manipulator, and verified the method by numerical simulation. Zhang et al.[20] deeply studied dynamics characteristics of joint clearance of 3-RRR planar parallel mechanism from all aspects of the moving platform by using the Newton Euler equation. Chen et al.[21] derived the dynamics equation of spatial parallel mechanism with clearances by the Newton Euler method, and studied the influence of the change of clearances value on its nonlinearity. Because it is difficult to calculate the constraints between components in complex mechanisms using the Newton Euler method, this work presents a dynamics modeling method of spatial mechanisms by using the Lagrange multiplier method, which is universal and simple. Xu and Li[22] established the model of planar two degree of freedom parallel mechanism using the method of multi-body system dynamics, and studied the influence of multiple rotating joint clearances on the collision of moving platform.
For spatial spherical joint clearance in spatial parallel mechanism, a general method of establishing dynamics equation of 4UPS-UPU mechanism with spherical clearance by Lagrange multiplier method is proposed. The impact of different friction coefficients on dynamics characteristics of mechanism is discussed, and the influence of different factors on chaos characteristics of parallel mechanism is further studied. The structure of this paper is as follows. In Section 1, kinematics model for spherical joint with clearance is built by using geometric relationship between sphere and spherical sleeve. In Section 2, according to the characteristics of contact collision, the L-N collision force model and modified Coulomb friction model are used to establish force model at clearance joint. In Section 3, by using the Lagrange multiplier method, dynamics equation of parallel mechanism containing spherical joint clearance is derived. In Section 4, dynamics equation is numerically solved and simulated by using MATLAB. Dynamics responses of the mechanism at clearance and influences of different factors on non-linear characteristics of mechanism are studied considering the different friction coefficients.
1 Kinematic Model of Spherical Joint with Clearance 1.1 Eccentricity between Spherical Joint with Clearance ConnectionsAccording to the internal structure and assembly relationship of the spherical joint, two cases were considered. The first one is that the spherical joint's sphere and the spherical sleeve's spherical center are merged under ideal conditions, and the outer wall of the sphere and the inner wall of the spherical sleeve completely contact and coincide, i.e., the clearance between the sphere and the spherical sleeve is 0. From the aspect of degree of freedom, there are three degrees of freedom between the sphere and the sleeve. The second is that in the non-ideal situation, the sphere and the sphere sleeve's center do not always coincide because of the existence of clearance, so that sphere can move freely in sphere sleeve, and contact mode between them changes from the original surface contact to point contact and has 6 DOF. The expression of the relative position between clearance elements is shown in Fig. 1. S2 represents the center of spherical sleeve, RS2 is the spherical sleeve radius, b2 represents the center of sphere, Rb2 represents the radius of sphere, Ann and Att are the normal and tangential vectors of plane, respectively.
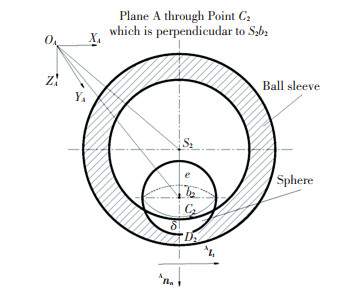
|
Fig.1 Schematic diagram of element position of clearance joint |
{A} represents the system coordinate system, {B} represents local coordinate system of the moving platform. The specific position can be seen in Fig. 2.

|
Fig.2 Structure sketch of 4UPS-UPU mechanism with clearance |
Ideally, position coordinates of spherical center b2 in fixed coordinate system can be written as
| $ { }^{A} \boldsymbol{P}_{b 2}={ }_{B}^{A} \boldsymbol{R}^{B} \boldsymbol{P}_{b 2}+{ }^{A} \boldsymbol{P}_{B O} $ | (1) |
where
The position coordinates of spherical sleeve center S2 in {A} can be expressed as
| $ { }^{A} \boldsymbol{P}_{S 2}={ }_{B}^{A} \boldsymbol{R}^{B} \boldsymbol{P}_{S 2}+{ }^{A} \boldsymbol{P}_{B O} $ | (2) |
where BPS2 represents center position vector of spherical sleeve under the {B}. According to Eqs.(1) and (2), the clearance position vector can be expressed as
| $ { }^{A} \boldsymbol{e}={ }^{A} \boldsymbol{P}_{b 2}-{ }^{A} \boldsymbol{P}_{S 2}={ }_{B}^{A} \boldsymbol{R}^{B} \boldsymbol{P}_{b 2}+{ }^{A} \boldsymbol{P}_{B O}-{ }_{B}^{A} \boldsymbol{R}^{B} \boldsymbol{P}_{S 2}-{ }^{A} \boldsymbol{P}_{B O} $ | (3) |
The clearance vector mode length at any time can be obtained as follows:
| $ e=\sqrt{{ }^{A} \boldsymbol{e}^{\mathrm{T}}\ { }^{A} \boldsymbol{e}} $ | (4) |
Then normal unit vector of contact surface between sphere and spherical sleeve can be expressed by the upper formula
| $ { }^{A} \boldsymbol{n}_{n}=\frac{{ }^{A} \boldsymbol{e}}{\boldsymbol{e}} $ | (5) |
During movement of sphere and spherical sleeve, contact deformation will occur if they contact each other. The contact deformation (contact depth) of the sphere and the spherical sleeve is as follows:
| $ \delta=e-c $ | (6) |
where c represents clearance radius, and c=RS2-Rb2. Rb2 and RS2 are the radius of the sphere and the sleeve, respectively.
According to the contact depth, it can be clearly judged whether the two components with clearance have contact collision. The judging conditions are as follows:
| $ \left\{\begin{array}{l} \delta>0, \text { contact and deform } \\ \delta=0, \text { critical point of contact and disengagement } \\ \delta<0, \text { no contact or free state } \end{array}\right. $ | (7) |
When δ≥0, it is assumed that point C2 and point D2 are potential contact points on the component, respectively. Then, position vectors of potential contact points in the {A} are as follows:
| $ { }^{A} \boldsymbol{P}_{C 2}={ }^{A} \boldsymbol{P}_{S 2}+R_{S 2} \cdot{ }^{A} \boldsymbol{n}_{n} $ | (8) |
| $ { }^{A} \boldsymbol{P}_{D 2}={ }^{A} \boldsymbol{P}_{b 2}+R_{b 2} \cdot{ }^{A} \boldsymbol{n}_{n} $ | (9) |
The derivation of the above two formulas is as follows:
| $ { }^{A} \boldsymbol{V}_{C 2}={ }^{A} \boldsymbol{V}_{S 2}+\boldsymbol{R}_{S 2} \cdot{ }^{A} \boldsymbol{\boldsymbol {\dot n }}_{n} $ | (10) |
| $ { }^{A} \boldsymbol{V}_{D 2}={ }^{A} \boldsymbol{V}_{b 2}+R_{b 2} \cdot{ }^{A} \boldsymbol{\boldsymbol {\dot n }}_{n} $ | (11) |
where
| $ { }^{A} \boldsymbol{V}_{S 2}={ }^{A} \boldsymbol{\omega}_{B O} \times{ }^{A} \boldsymbol{r}_{S 2}+{ }^{A} \boldsymbol{V}_{B O} $ | (12) |
| $ { }^{A} \boldsymbol{V}_{b 2}={ }^{A} \boldsymbol{\omega}_{B O} \times{ }^{A} \boldsymbol{r}_{\mathrm{b} 2}+{ }^{A} \boldsymbol{V}_{B O} $ | (13) |
Among them, AωBO represents angular velocity of moving platform under the {A}.
By solving Eqs.(10) and (11) above, relative normal and tangential velocity can be obtained. The expressions are as follows:
| $ { }^{A} \boldsymbol{V}_{n}=\left[\left({ }^{A} \boldsymbol{V}_{D 2}-{ }^{A} \boldsymbol{V}_{C 2}\right)^{\mathrm{T}} \cdot{ }^{A} \boldsymbol{n}_{n}\right] \cdot{ }^{A} \boldsymbol{n}_{n} $ | (14) |
| $ { }^{A} \boldsymbol{V}_{t}=\left({ }^{A} \boldsymbol{V}_{D 2}-{ }^{A} \boldsymbol{V}_{C 2}\right)-{ }^{A} \boldsymbol{V}_{n} $ | (15) |
The expression of relative tangential velocity can be given by
| $ \boldsymbol{V}_{t}=\sqrt{{ }^{A} \boldsymbol{V}_{t}^{\mathrm{T}\ A} \boldsymbol{V}_{t}} $ | (16) |
After L-N normal contact collision force model[7], many scholars used experimental methods to verify the credibility of the model. There is only a minor error between the experimental results and the theory, and the error is within consideration. This provides a reliable collision force model for future researchers. The L-N model is compared with other normal contact force models in some key positions, which can obtain more accurate results under low collision velocity and conditions of high recovery coefficient. Therefore, the L-N model will be used to solve the problem.
The expression of normal contact force Fn in contact collision of accessory elements is as follows:
| $ F_{n}=K_{S} \delta^{m}\left[\begin{array}{c} 1+\frac{3\left(1-c_{r}^{2}\right) \cdot \dot{\delta}}{4 \dot{\delta}_{0}} \end{array}\right] $ | (17) |
where
| $ K_{S}=\frac{4}{3\left(\sigma_{S 2}+\sigma_{b 2}\right)} \sqrt{\frac{R_{S 2} R_{b 2}}{R_{S 2}+R_{b 2}}} $ |
| $ \sigma_{S 2}=\frac{1-v_{S 2}^{2}}{E_{S 2}}, \sigma_{b 2}=\frac{1-v_{b 2}^{2}}{E_{b 2}} $ |
In the equation, Rb2 and RS2 are the radius of the sphere and the sleeve, respectively. Eb2 and ES2 are the coefficients related to materials, and their physical meanings represent elastic modulus. m is the parameter related to the metals, the value of which is 1.5. vb2 and vS2 represent Poisson's ratio of materials. δ is the deformation of contact collision, which is used to judge whether contact collision occurs or not. cr is the coefficient of recovery. The harder the general material, the greater its value[23]. δ is the penetration velocity of the sphere center relative to sphere sleeve center. δ0 represents initial collision velocity, and is determined by initial contact deformation speed of each collision process. KS is contact stiffness coefficient.
2.2 Establishment of Tangential Contact Force ModelCoulomb tangential friction model[24] is more common in dynamic modeling of multi-body system, but the model solution is prone to singular problems because of its discontinuity. μd is introduced into modified friction model[25], which solves the numerical integral instability when relative velocity is near zero.
The tangential contact force is written as
| $ F_{t}=-\mu_{s} \mu_{d} F_{n} \frac{v_{t}}{\left|v_{t}\right|} $ | (18) |
where μs is sliding friction coefficient; μd is dynamics correction factor, which divides the following boundaries according to the different velocities as follows:
| $ \mu_{d}=\left\{\begin{array}{ll} 1, & \left|v_{t}\right|>v_{1} \\ \frac{\left|v_{t}\right|-v_{0}}{v_{1}-v_{0}}, & v_{0} \leqslant\left|v_{t}\right| \leqslant v_{1} \\ 0, & \left|v_{t}\right|<v_{0} \end{array}\right. $ | (19) |
where v0 and v1 are predetermined speed limit values, which are used to determine the speed to find out the dynamic correction coefficient.
Through the above solution, the contact force with clearance is as follows:
| $ \boldsymbol{F}_{f}=F_{n}{}^{A} \boldsymbol{n}_{n}+F_{t}{}^{A} \boldsymbol{t}_{t} $ | (20) |
Mechanism sketch of 4UPS-UPU is shown in Fig. 2. The mechanism consists of a movable platform, a fixed platform, four UPS drive branches connecting two platforms, and one UPU drive branch. There are 12 components in total, among which there is one fixed component. The fixed platform is a fixed part in this organization, so that its number is 0. The five driving rods linked with moving platform are numbered 1, 2, 3, 4, and 5; the five swing rods linked with fixed platform are numbered 6, 7, 8, 9, and 10; and the moving platform is numbered 11. The serial numbers of the universal joints described below correspond to the subscript numbers of joints. The radius of fixed platform is 0.65 m; universal joint 2, 3, 4, and 5 are evenly distributed; universal joint 1 is at the middle angle between 2 and 3 and distance from fixed platform center is 0.71 m; radius of the moving platform is 0.202 m; universal joint 1, 2, 3, 4, and 5 are evenly distributed on fixed platform. A fixed coordinate system OA-XAYAZA is established on a fixed platform, and the symbols are denoted by {A}. The moving platform is an end-effector in this mechanism, on which a moving coordinate system o11- x11y11z11 is founded. Local coordinate system oi-xiyizi i=1, 2, …, 10 is established on each rod of branched chain. The coordinate origin is attached at mass center of rod (assuming that centroid coincides with geometric center). xi axis is downward along the rod, and yi axis is perpendicular to the direction of the rod and parallel to one of the axes of the universal joint. Considering the indirect and direct influence of the joint on motion characteristics of moving platform, the joint directly connected with the moving platform was selected as the clearance joint[27]. Because the spherical joints account for the largest proportion of the joints directly connected with the moving platform, this paper assumes that there was a clearance between the second bar of the mechanism and the spherical joint s2 connected with the moving platform.
3.2 Establishment of Dynamic Equation ModelIn spatial multi-body system, motion equations are usually established by joint constraints. In order to accurately describe the kinematic state and attitude of each component at every moment, the rotation matrix of each component is determined by using the Euler angle of X-Z-Y rotation sequence. Generalized coordinates of the system are as follows:
| $ \boldsymbol{q}=\left[\begin{array}{llll} \boldsymbol{q}_{1}^{\mathrm{T}} & \boldsymbol{q}_{2}^{\mathrm{T}} & \cdots & \boldsymbol{q}_{11}^{\mathrm{T}} \end{array}\right]^{\mathrm{T}} $ | (21) |
where
Therefore, the rotation matrix obtained from the rotation order X-Z-Y is expressed as
| $ \boldsymbol{R}_{i}=\boldsymbol{R}_{x i} \cdot \boldsymbol{R}_{z i} \cdot \boldsymbol{R}_{y i}=\left[\begin{array}{ccc} \mathrm{c} \beta_{i} \cdot \mathrm{c} \gamma_{i} & -\mathrm{s} \gamma_{i} & \mathrm{c} \gamma_{i} \cdot \mathrm{s} \beta_{i} \\ \mathrm{~s} \alpha_{i} \cdot \mathrm{s} \beta_{i}+\mathrm{c} \alpha_{i} \cdot \mathrm{c} \beta_{i} \cdot \mathrm{s} \gamma_{i} & \mathrm{c} \alpha_{i} \cdot \mathrm{c} \gamma_{i} & \mathrm{c} \alpha_{i} \cdot \mathrm{s} \beta_{i} \cdot \mathrm{s} \gamma_{i}-\mathrm{c} \beta_{i} \cdot \mathrm{s} \alpha_{i} \\ \mathrm{c} \boldsymbol{\beta}_{i} \cdot \mathrm{s} \alpha_{i} \cdot \mathrm{s}\beta_{i}+\mathrm{c} \alpha_{i} \cdot \mathrm{s} \beta_{i} & \mathrm{c} \gamma_{i} \cdot \mathrm{s} \alpha_{i} & \mathrm{c} \alpha_{i} \cdot \mathrm{c} \beta_{i}+\mathrm{s} \alpha_{i} \cdot \mathrm{s} \beta_{i} \cdot \mathrm{s} \gamma_{i} \end{array}\right] \quad(i=1,2, \cdots, 11) $ | (22) |
where c is the cosine function cos and sis the sine function sin.
Fig. 3(a) shows the universal joint constraint. It connects two parts i and j, and the universal joint center is point Q. pi and pj are position vectors of the origins of local coordinates in global coordinates, respectively. QOi and QOj represent two directional vectors fixed on components i and j, which are located on the axis of the rotary joint, respectively. Obviously, QOi and QOj remain orthogonal at all times. oiq and ojq represent the position vectors from origin to point Q. Since universal joint can constrain four degrees of freedom in space, the universal joint constraint equation is as follows:
| $ \boldsymbol{\varPhi}_{U k}=\left[\begin{array}{c} \boldsymbol{p}_{i}+\boldsymbol{R}_{i} \boldsymbol{o}_{i}{ }^{q}-\boldsymbol{p}_{j}+\boldsymbol{R}_{j} \boldsymbol{o}_{j}{ }^{q} \\ \left(\boldsymbol{Q}_{O i}\right){ }^{\mathrm{T}} \cdot \boldsymbol{Q}_{O{j}} \end{array}\right]=0_{4 \times 1}(k=1,2, \ldots, 6) $ | (23) |

|
Fig.3 Schematic diagram of constraints of spatial motion joints |
where QOi and QOj are unit vectors and their expressions are as follows:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{Q}}_{O1}} = {{\left[ {\begin{array}{*{20}{l}} 0&0&1 \end{array}} \right]}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{Q}}_{O2}} = {{\left[ {\begin{array}{*{20}{l}} 0&{ - \cos \frac{{\rm{ \mathsf{ π} }}}{4}}&{\cos \frac{{\rm{ \mathsf{ π} }}}{4}} \end{array}} \right]}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{Q}}_{O3}} = \left[ {\begin{array}{*{20}{l}} 0&{\cos \frac{{{\rm{3 \mathsf{ π} }}}}{4}}&{{{\left. {\cos \frac{{{\rm{3 \mathsf{ π} }}}}{4}} \right]}^{\rm{T}}}} \end{array}} \right.}\\ {{\mathit{\boldsymbol{Q}}_{O4}} = \left[ {\begin{array}{*{20}{l}} 0&{\cos \frac{{{\rm{7 \mathsf{ π} }}}}{4}}&{{{\left. { - \cos \frac{{{\rm{7 \mathsf{ π} }}}}{4}} \right]}^{\rm{T}}}} \end{array}} \right.}\\ {{\mathit{\boldsymbol{Q}}_{O5}} = \left[ {\begin{array}{*{20}{l}} 0&{\cos \frac{{\rm{ \mathsf{ π} }}}{4}}&{{{\left. {\cos \frac{{\rm{ \mathsf{ π} }}}{4}} \right]}^{\rm{T}}}} \end{array}} \right.}\\ {{\mathit{\boldsymbol{Q}}_{O6}} = {{\left[ {\begin{array}{*{20}{l}} 0&0&1 \end{array}} \right]}^{\rm{T}}}} \end{array}(i = 1,2, \ldots ,6)} \right. $ | (24) |
| $ \boldsymbol{Q}_{O{j}}=\boldsymbol{R}_{j} \cdot\left[\begin{array}{lll} 0 & 1 & 0 \end{array}\right]^{\mathrm{T}}(j=6,7,8,9,10,1) $ | (25) |
Fig. 3(c) is a sketch of prismatic joint constraints. In order to describe the prismatic joint constraints more intuitively, a direction vector was introduced at the center of each component, where the expression of each vector is
| $ \boldsymbol{g}_{i}=\boldsymbol{R}_{i} \cdot\left[\begin{array}{lll} -1 & 0 & 0 \end{array}\right]^{\mathrm{T}}(i=1,2, \ldots, 5) $ |
| $ \boldsymbol{f}_{i} =\boldsymbol{R}_{i} \cdot\left[\begin{array}{lll} 0 & 1 & 0 \end{array}\right]^{\mathrm{T}}(i=1,2, \ldots, 5) $ |
| $ \boldsymbol{g}_{j}=\boldsymbol{R}_{j} \cdot\left[\begin{array}{lll} 1 & 0 & 0 \end{array}\right]^{\mathrm{T}}(j=6,7, \ldots, 10) $ |
| $ \boldsymbol{f}_{j} =\boldsymbol{R}_{j} \cdot\left[\begin{array}{lll} 0 & 0 & 1 \end{array}\right]^{\mathrm{T}}(j=6,7, \ldots, 10) $ |
In particular, a vector is introduced between two components i and j as a common direction vector ln, and the prismatic joint can constrain five degrees of freedom in space, so constraint equation of prismatic joint is as follows:
| $ \boldsymbol{\varPhi}_{P k}=\left[\begin{array}{ll} \boldsymbol{g}_{i} \times \boldsymbol{g}_{j} \\ \boldsymbol{g}_{i} \times \boldsymbol{l}_{n} \\ \boldsymbol{f}_{i}^{\mathrm{T}} \cdot \boldsymbol{f}_{j} \end{array}\right]=0_{5 \times 1}(k=1,2, \ldots, 5) $ | (26) |
Fig. 3(d) is a schematic diagram of spherical joints constraints. The point Q is the spherical center of sphere and spherical sleeve. In spatial mechanism, spherical joints can constrain three degrees of freedom. Assuming that there is a clearance between the second bar of 4UPS-UPU mechanism and the joint s2 linked with moving platform, without considering the constraints at s2 of the spherical joint, the constraints equation of the spherical joint is as follows:
| $ \boldsymbol{\varPhi}_{S k}=\boldsymbol{p}_{i}+\boldsymbol{R}_{i} \boldsymbol{o}_{i}{ }^{q}-\boldsymbol{p}_{j}-\boldsymbol{R}_{j} \boldsymbol{o}_{j}{ }^{q}=0_{3 \times 1}(k=3,4,5) $ | (27) |
In this mechanism, the prismatic member is the driving member. Because the mechanism has 5 DOF, in order to give the mechanism some motion, five driving equations were added. Because inverse solution of parallel mechanism is simple, the kinematic equation of each driving rod can be obtained by inverse kinematic solution. Five driving equations need five constraint equations, so the constraint equation is as follows:
| $ \boldsymbol{\varPhi}_{D}=\left|\boldsymbol{l}_{n}\right|-\boldsymbol{h}_{n}(t)=0_{5 \times 1}(n=1,2, \ldots, 5) $ | (28) |
where hn(t) represents displacement driving function, which means that distance between point Q and point P in Fig. 3(c) varies with time. ln represents distance between point Q and point P in geometric sense, and the distance between the constructed position driving function and the two points in geometric sense should be kept equal at all times.
In this study, it was assumed that there was a clearance between the second bar of 4UPS-UPU mechanism and the joint s2 linked with moving platform.So the constraints at s2 were not considered in the constraints equation of the system, and the constraints equation of the 4UPS-UPU mechanism with the clearance at s2 is as follows:
| $ \boldsymbol{\varPhi}=\left[\begin{array}{lllll} \boldsymbol{\varPhi}_{U 1}{ }^{\mathrm{T}} & \boldsymbol{\varPhi}_{U 2}{ }^{\mathrm{T}} & \boldsymbol{\varPhi}_{U 3}{ }^{\mathrm{T}} & \boldsymbol{\varPhi}_{U 4}{ }^{\mathrm{T}} & \boldsymbol{\varPhi}_{U 5}{ }^{\mathrm{T}} \\ \boldsymbol{\varPhi}_{U 6}{ }^{\mathrm{T}} & \boldsymbol{\varPhi}_{P 1}{ }^{\mathrm{T}} & \boldsymbol{\varPhi}_{P 2}{ }^{\mathrm{T}} & \boldsymbol{\varPhi}_{P 3}{ }^{\mathrm{T}} & \boldsymbol{\varPhi}_{P 4}{ }^{\mathrm{T}} \\ \boldsymbol{\varPhi}_{P 5}{ }^{\mathrm{T}} & \boldsymbol{\varPhi}_{S 3}{ }^{\mathrm{T}} & \boldsymbol{\varPhi}_{S 4}{ }^{\mathrm{T}} & \boldsymbol{\varPhi}_{S 5}{ }^{\mathrm{T}} & \boldsymbol{\varPhi}_{D}{ }^{\mathrm{T}} \end{array}\right]^{\mathrm{T}}=0_{63 \times 1} $ | (29) |
Based on the above constraints, the differential-algebraic dynamic equations with spherical joint clearance 4UPS-UPU mechanism is as follows:
| $ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over M} }}}&{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_q^{\rm{T}}}\\ {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_q}}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\ddot q}}}\\ \mathit{\boldsymbol{\lambda }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}\\ \mathit{\boldsymbol{\gamma }} \end{array}} \right] $ | (30) |
where Φq represents the derivation of Φ in generalized coordinates q and the Jacobian matrix of Φ. ΦqT is the transposition of
| $ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over M} }}}&{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_q^{\rm{T}}}\\ {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_q}}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\ddot q}}}\\ \mathit{\boldsymbol{\lambda }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}\\ {\mathit{\boldsymbol{\gamma '}}} \end{array}} \right] $ | (31) |
where
In this section, the mechanism 4UPS-UPU was used to show dynamics characteristics of clearance with spherical joint due to change of friction coefficient. In this mechanism, it is assumed that there was a clearance at s2. In order to better show the dynamic characteristics, this example gives a periodic function to the moving platform. Then the driving function of the driving rod was obtained by inverse kinematics solution. With the help of SolidWorks three-dimensional model, the basic mechanism parameters of 4UPS-UPU mechanism components are shown in Table 1. Physical performance parameters of sphere and spherical sleeve at s2 are shown in Table 2, and dynamics simulation parameters of mechanism 4UPS-UPU with clearance are shown in Table 3, where c2 represents the clearance radius at s2. Finally, the above system parameters and displacement motion law of the moving platform were used as input parameters to solve the dynamic equation, and the specific solution ideas are shown in Fig. 4 of the flowchart. Since the mechanism has 5DOF, the motion law of moving platform in this example is given as follows:
| $ \left\{ {\begin{array}{*{20}{l}} {X = 1.1}\\ {Y = 0.05\sin ({\rm{ \mathsf{ π} }}t)}\\ {Z = 0.05\cos ({\rm{ \mathsf{ π} }}t)}\\ {\beta = 0}\\ {\gamma = 0} \end{array}} \right. $ | (32) |
| Table 1 Basic mechanism parameters of each component of 4UPS-UPU parallel mechanism |
| Table 2 Physical performance parameters of spheres and sleeves |
| Table 3 Dynamics simulation parameters of mechanism 4UPS-UPU with spherical joint clearance |
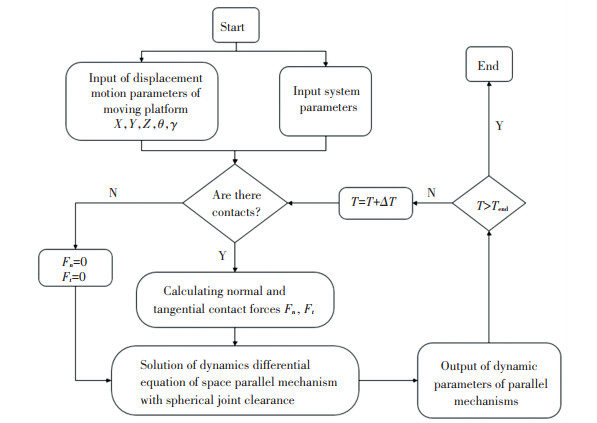
|
Fig.4 Flow chart of dynamic solution |
4.2 Dynamic Response Analysis
Firstly, the model was solved numerically by using MATLAB, and the output response of the 4UPS-UPU moving platform under ideal motion joint was obtained. Then, the output response of moving platform was respectively obtained under the influence of two friction coefficients of 0.05 and 0.10. In the simulation process, the system was in an unstable state at the beginning because of the existence of clearance, so the results of the two periods intercepted in the figure below are that the system was in a stable period, and the results were compared with the output response of the moving platform under the ideal motion joint conditions.
Fig. 5 shows comparison curves of center of the mass displacement of moving platform with different friction coefficient values and ideal conditions when there is clearance at s2. As shown in Fig. 5(a1), in X direction, displacement curves of two different friction coefficients basically coincide, but the difference between the displacement curves of the two friction coefficients and that of the ideal case is 0.1 mm in the longitudinal coordinates. Fig. 5(a2) shows that the displacement curves of the two friction coefficients are identical in the longitudinal coordinates, but there are still very small differences in the images. It can be concluded that there is a small offset of the moving platform in X direction in the case of clearance. As shown in Fig. 5(b1) and (c1), the displacement curves of two friction coefficients coincide with ideal curve, but the displacement curves under different friction coefficients can be seen from the enlarged Fig. 5(b2) and (c2), where there are slight deviations from the displacement curves under ideal conditions. It is found that friction coefficient has little effect on moving platform, and there is a slight deviation in the direction of displacement.
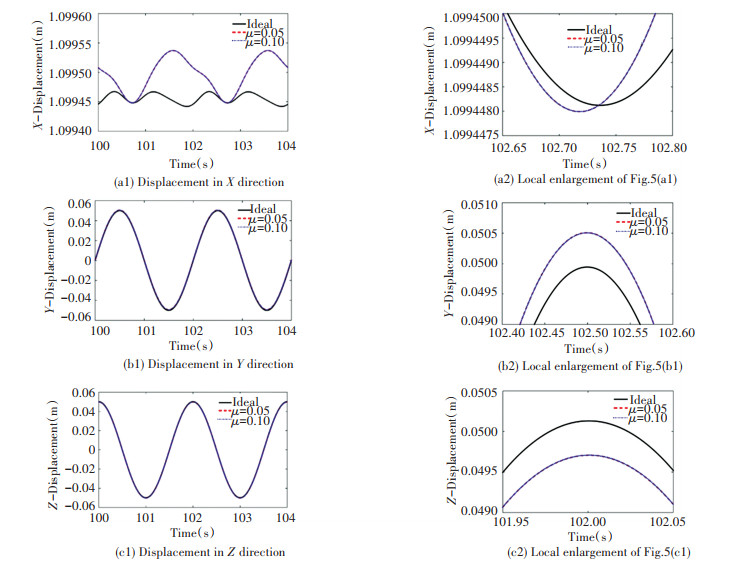
|
Fig.5 Displacement of moving platform center under different friction coefficients |
Fig. 6 is comparison curves of the velocities of the moving platform centroid under different friction coefficients with those under ideal conditions. As shown in Fig. 6(a1), the velocity curves of two friction coefficients with clearance basically coincide, but there are some differences between them and the ideal situation, and they are roughly around the ideal situation. Fig. 6(a2) shows that there is a slight difference between the velocity curves under the two friction coefficients. At the trough of the curve, the effect of friction coefficient 0.05 on the velocity of moving platform is slightly greater than 0.1. In Fig. 6(b1) and (c1), the velocity curves of the two friction coefficients in Y and Z directions are basically the same as those in ideal case. However, through the enlarged Fig. 6(b2) and (c2), it can be seen that the velocity curves under different friction coefficients are slightly deviated from those under ideal conditions and slight offset occurs, and the friction coefficient of the three curves is 0.05, which has a greater influence on the moving platform. From the above analysis, the influence of friction coefficient on velocity and displacement of moving platform is basically similar.
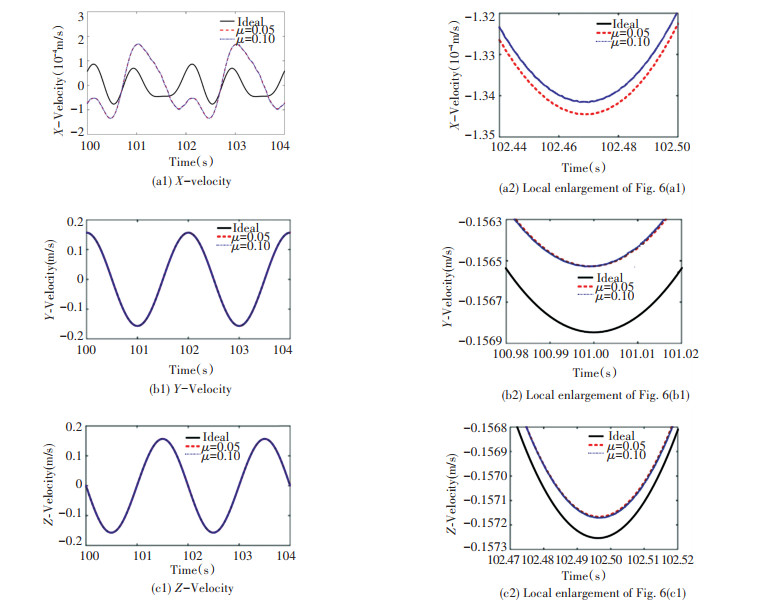
|
Fig.6 Velocity of center of moving platform under different friction coefficients |
Fig. 7 is comparison curves of acceleration of the moving platform centroid under different friction coefficients with those under ideal conditions. As shown in Fig. 7(a), it is obvious that the acceleration curves of two friction coefficients with clearance have high frequency vibration and fluctuate up and down at the ideal curve. But when the friction coefficient is 0.05, the span of the curve is larger. The results show that when the friction coefficient is 0.05, the effect of acceleration of motion platform is greater than that when the friction coefficient is 0.1. As shown in Fig. 7(b1) and (c1), it is obvious that the amplitude of the acceleration curve changes when friction coefficient is 0.05, while acceleration curve with friction coefficient of 0.10 is basically consistent with the curve trend under ideal conditions. Fig. 7(b2) and (c2) show that under the effect of clearance, acceleration curve has undergone intense high-frequency vibration. When the friction coefficient is 0.05, the deviation degree of the curve is greater than that when the friction coefficient is 0.10. The reason may be that the system is too chaotic because of the excessively small friction coefficient, which results in large errors in the solution process. From the above analysis, the smaller the friction coefficient, the greater the deviation of curve. In general, compared with displacement and velocity, friction coefficient has more influence on acceleration of moving platform.

|
Fig.7 Acceleration of moving platform center under different friction coefficients |
4.3 Contact Force at Clearance
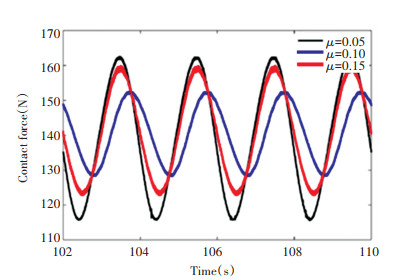
Fig. 8 shows the time-dependent curves of contact force at the clearance of spherical joint s2 when the friction coefficient is 0.05, 0.10, and 0.15, respectively. The curves were analyzed in four periods. The graph shows that the contact force curve has obvious high-frequency vibration, and the change law of the curve is similar with that of sine wave. The quantitative analysis shows that when the friction coefficient is 0.05, the contact force reaches the minimum value of 115.4 N at 108.4 s and the maximum value of 162.7 N at 103.5 s; when the friction coefficient is 0.10, contact force reaches the minimum value of 127.9 N at 102.8 s and the maximum value of 152.8 N at 105.8 s, and the maximum span is less than that at 0.05 friction coefficient. When friction coefficient is 0.15, contact force reaches the minimum value of 122.5 N at 102.5 s and the maximum value of 160.1 N at 107.5 s, and the maximum span is greater than that at 0.10 friction coefficient. Through the above quantitative analysis, it is found from careful observation that the change of contact force and friction coefficient has certain rules, and the change of contact force and friction coefficient is not in positive proportion. Among the three friction coefficient values, the amplitude of contact force corresponding to 0.10 is the smallest, and the amplitude of contact force corresponding to 0.05 is greater than that of the friction coefficient of 0.15. Therefore, in practical engineering, the material selection of ball and sleeve should be based on a suitable friction coefficient to effectively control the amplitude of contact force to a relatively small range.
|
Fig.8 Contact forces with different friction coefficients at spherical joints |
4.4 Nonlinear Characteristics of Moving Platform and Clearance under Different Factors
Fig. 9 is phase trajectory and Poincare map of moving platform in Z direction with different friction coefficients. For a more intuitive comparison, the following three representative friction coefficients were chosen to be 0.01, 0.05, and 0.10, respectively. As shown in Fig. 9(a) and (b), when friction coefficient is 0.01, the phase diagram of moving platform is an irregular circular ring with a certain width. Its width mainly concentrates on the upper and lower parts, and the lines at the left and right parts are narrow. The Poincare mapping mainly concentrates on the points with a certain length. So the moving platform is quasi-periodic under the action of friction coefficient. In Fig. 9(c) and (d), when friction coefficient is 0.05, phase diagram of moving platform is irregularly circular, and its width is narrow. At the same time, observing its Poincare mapping, it can be seen that the moving platform is mainly concentrated on one point, so it can be judged that the moving platform is in a one-cycle motion state. Fig. 9(e) and (f) show the phase trajectory and Poincare map when friction coefficient is 0.10. The figure is basically the same as when the friction coefficient is 0.05, so moving platform is also in a single period state at this time. When friction coefficient increases gradually, image range of phase diagram and Poincare diagram gradually reduces to a stable figure, i.e., the motion state of moving platform tends to be stable.

|
Fig.9 Phase trajectory and Poincare map of moving platform in Z direction with different friction coefficients |
Fig. 10 is a bifurcation diagram of the moving platform in three directions, in which longitudinal coordinates of the figure represent the relative velocity and the horizontal coordinates represent the variation of the friction coefficient from 0.01 to 0.20. As shown in the bifurcation diagram of Fig. 10(a)-(c), there are no obvious bifurcation phenomena in the graph, and most of them are in the state of single-period motion. Only when the friction coefficient is small, they are in the state of quasi-periodic motion. Through the above analysis, the advantages of the stability of parallel mechanism can be seen. Even though friction coefficient is very small, the moving platform still keeps periodic motion. Increasing friction coefficient properly is beneficial to improve the stability of the moving platform.

|
Fig.10 Bifurcation diagrams of different friction coefficients of moving platform in three axis directions |
Fig. 11 is a phase trajectory diagram of the spherical joint clearance s2 in Y direction and a corresponding Poincare map for different friction coefficients with different friction coefficients. For a more intuitive comparison, the following three representative friction coefficients were chosen to be 0.01, 0.05, and 0.10, respectively. Fig. 11(a) and (b) show that the phase diagrams at the clearance are numerous irregular rings intertwined with each other when friction coefficient is 0.01, which is in great disorder. Some of its Poincare maps focus on a very small range, and some discrete and non-coincident points are distributed around it. It is preliminarily judged that motion state at clearance position under the friction coefficient is chaotic. As shown in Fig. 11(c) and (d), when friction coefficient is 0.05, phase diagram at clearance is irregularly circular with a wide width. At the same time, its Poincare map shows that a vertical line composed of numerous points distributed in the middle and upper parts, thus it can be judged that clearance position is in quasi-periodic motion. Fig. 11(e) and (f) show when friction coefficient is 0.10, the figure is still irregularly circular and the width is narrow when the friction coefficient is 0.05. Poincare mapping shows that the length of the line decreases, so the motion state at the clearance is quasi-periodic and the number of periods is less than that at the friction coefficient of 0.05. By comparing the three friction coefficients, it can be found that with the increase of their values, the chaotic state of phase diagram and Poincare map gradually weakens, the width and length of lines decrease to a stable figure, and the motion state at clearance position also changes from chaotic to quasi-periodic.

|
Fig.11 Phase trajectory and Poincare map of joint clearance in Y direction with different friction coefficients |
Fig. 12 is a bifurcation diagram of clearance in three axis directions. The longitudinal coordinates of the figure represent the relative velocity and the horizontal coordinates represent the variation of friction coefficient from 0.01 to 0.20. As shown in the bifurcation diagram of Fig. 12 (a)-(c), the state of motion at clearance changes from chaotic state to quasi periodic state as friction coefficient increases in turn. According to the trend of the graph, the motion state becomes more and more stable. Within the friction coefficient range of 0.010 to 0.022, clearance is always in chaotic state, and the degree of its state can be seen to be weakened. In the middle region, the stability of clearance is higher in the small range of friction coefficient near 0.07 and 0.10.

|
Fig.12 Bifurcation diagrams of different friction coefficients in three axis directions of spherical joint clearance |
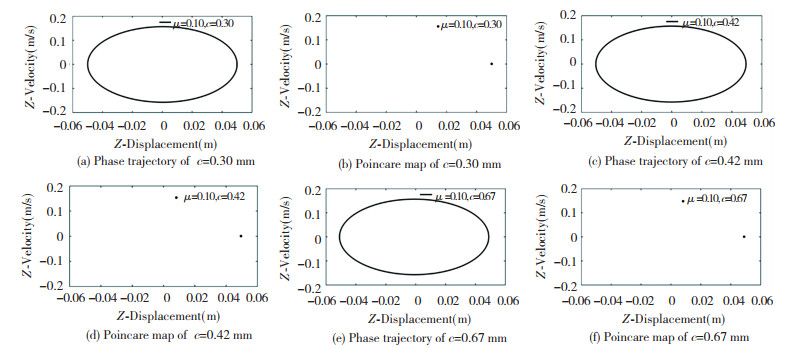
Through impact of different friction coefficients on non-linear characteristics of moving platform and clearance location, the following choices are made when the friction coefficient is 0.10 to study the impact of multiple clearance values on non-linear characteristics of clearance location and moving platform, in which the range of clearance values is (0, 0.9). As shown in Fig. 13, the following three clearance values with obvious characteristics are 0.30 mm, 0.42 mm, and 0.67 mm, respectively. Fig. 13(a) and (b) show when c=0.30 mm, phase diagram of moving platform is similar to an ellipse, its lines are concentrated on a line, and its Poincare mapping is concentrated on a point. Thus, moving platform is in a periodic motion state under its clearance value, and the motion state is a single period. Fig. 13(c)-(f) show the same form and size as Fig. 13(a) and (b). When the clearance value increases, it is obvious that moving platform always keeps a single period motion state.
|
Fig.13 Phase trajectory and Poincare map of moving platform in Z direction with different clearance values |
Fig. 14 is a bifurcation diagram of moving platform in three axis directions, in which longitudinal coordinates of the figure represent the speed and the horizontal coordinates represent the change of the clearance value from 0 to 0.9. As shown in the bifurcation diagram of Fig. 14(a)-(c), there is no bifurcation on the moving platform, and each figure is a point under the corresponding clearance value display, which indicates that the moving platform is always in a single cycle motion within the clearance value range. Through the above analysis, when clearance value changes, the parallel mechanism is still stable and remains unchanged or has little influence on it. The moving platform always keeps a state of motion under different clearance values. It can be seen that under the joint action of parallel branched chains, the stability of mechanism has been improved to some extent.

|
Fig.14 Bifurcation diagrams of different clearance values of moving platform in three axis directions |
Fig. 15 is phase trajectory and Poincare map of spherical joint s2 in Y direction at different clearance values. Fig. 15(a) and (b) show when c=0.30 mm, phase diagram at clearance presents a circular ring with wavy lines, and some positions have large fluctuations. Its Poincare map is projected to a line segment, which can be used to judge that the motion state is quasi-periodic. In Fig. 15(c) and (d), phase diagram shows a circular ring with a certain width, and its Poincare map is projected to a line segment. It can be judged that the velocity of the clearance fluctuates within a certain range under the clearance value, so its motion state is quasi-periodic. In Fig. 15(e) and (f), the order of magnitude of its graph is larger than that of Fig. 15(c). The phase diagram shows a series of lines around the circle, but some positions have large fluctuations. Its Poincare mapping concentrates on a small area and its motion state can be judged to be quasi-periodic. When clearance value increases, corresponding velocity and displacement range of the image can be concluded from the phase diagram and Poincare map, and fluctuation of the image is more intense. However, the quasi periodic motion state is always present, and the chaos does not appear.

|
Fig.15 Phase trajectory and Poincare map of clearance of spherical joint in Y direction with different clearance values |
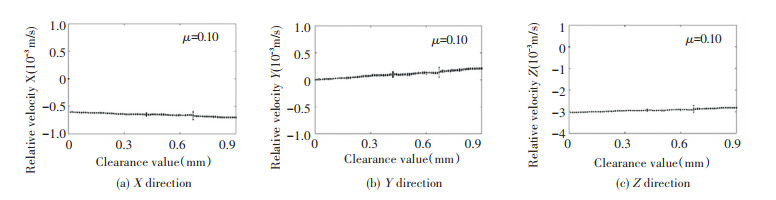
Fig. 16 is bifurcation diagrams of clearance joint in three axis directions, in which longitudinal coordinates of the figure represent the relative velocity and the horizontal coordinates represent the change of the clearance value from 0 to 0.9. As shown in the figure, there is no bifurcation at the clearance, and most of them are in quasi-periodic motion state. When c=0.42 mm, the corresponding velocity range becomes larger, and when c=0.67 mm, the corresponding velocity range reaches the maximum, but the corresponding motion state of the two clearances is still in quasi-periodic motion state. It shows that there is no chaotic motion in the clearance range. Through the above analysis, the above-mentioned two clearance values should be avoided when choosing the actual clearance value. Because of the requirement of mechanism accuracy, the clearance value below 0.30 mm can keep the motion state of clearance in good stability.
|
Fig.16 Bifurcation diagrams of different clearance values in three axis directions of spherical joint clearance |
4.5 Virtual Simulation Verification
In order to verify correctness of dynamic model, the ADAMS virtual simulation software was used to compare and analyze the established model. Clearance value of simulation parameters is 0.5 mm and the friction coefficient is 0.1. Other parameters are consistent with Table 2. As shown in Fig. 17, the acceleration in two directions can be seen from Fig. 17(a1) and (b1). At first, due to the randomness of collision at the clearance, there are differences between the two curves. However, when the acceleration is stable, it can be seen from Fig. 17(a2) and (b2) that the two curves basically coincide. As shown in Fig. 17(c1) and (c2), the comparative analysis of the contact force curve at spherical joint is consistent with the above description, and the two curves basically coincide when stable. Thus, the correctness of the model is verified.

|
Fig.17 Comparison chart of virtual simulation |
5 Conclusions
In this work, the dynamics model of spatial parallel mechanism with spherical clearance joint was developed, and the influence of friction coefficient and clearance size on the dynamics characteristics of the mechanism were analyzed. The main conclusions are as follows:
1) Geometric relationship of spherical joint with clearance was systematically described. A general method of establishing the dynamic equation of 4UPS-UPU parallel mechanism with spherical clearance by Lagrange multiplier method was proposed and dynamics equation was solved by Runge-Kutta method.
2) The influence of friction coefficient on dynamic response of 4UPS-UPU mechanism with spherical clearance joint was analyzed. Displacement, velocity, and acceleration curves of moving platform and contact force of clearance joint were all analyzed. Among the first three curves, acceleration is the most sensitive to the change of friction coefficient.
3) The chaos characteristics of 4UPS-UPU mechanism with spherical clearance joint under different factors were analyzed. With the decrease of friction coefficient at clearance joint, the motion state of clearance joint became unstable. When friction coefficient decreased to a certain value, chaos appeared. However, the moving platform had good stability and there was no chaos phenomenon. In the range of (0, 0.9), moving platform was always in periodic-one motion with the increase of clearance value. However, spherical joint was only quasi-periodic motion, and there was no chaotic phenomenon. Combining the analysis of these two factors, it can be concluded that change of clearance value has less influence on mechanism, and stability of moving platform is much higher than that of the spherical joint.
4) The research has theoretical guiding significance for improving the dynamic performance and avoiding chaos of parallel mechanisms including spherical joint clearance. Our future research will be focused on the influence of wear factor and lubrication effect on dynamic characteristics of mechanism.
| [1] |
Ting K L, Zhu J M, Watkins D. The effects of joint clearance on position and orientation deviation of linkages and manipulators. Mechanism & Machine Theory, 2000, 35(3): 391-401. DOI:10.1016/S0094-114X(99)00019-1 (  0) 0) |
| [2] |
Wang X P, Liu G, Ma S J, et al. Effects of clearance joint on impact dynamic characteristics of planar mechanisms. Journal of Vibration and Shock, 2017, 36(17): 74-78. (in Chinese) (  0) 0) |
| [3] |
Zhao Q Q, Guo J K, Hong J. Assembly precision prediction for planar closed-loop mechanism in view of joint clearance and redundant constraint. Journal of Mechanical Science & Technology, 2018, 32(7): 3395-3405. DOI:10.1007/s12206-018-0643-5 (  0) 0) |
| [4] |
Erkaya S. Clearance-induced vibration responses of mechanical systems: computational and experimental investigations. Journal of the Brazilian Society of Mechanical Sciences & Engineering, 2018, 40(2): 90. DOI:10.1007/s40430-018-1015-x (  0) 0) |
| [5] |
Duan L Y, An Z J, Yang R G, et al. Mechanical model of coupling rolling and sliding friction in real-time non-clearance precision ball transmission. Tribology International, 2016, 103: 218-227. DOI:10.1016/j.triboint.2016.06.032 (  0) 0) |
| [6] |
Chen X L, Chen T X, Li Y W, et al. Kinematics modeling and analysis of 3-PRR parallel robot mechanism. Journal of Shandong University of Science and Technology (Natural Science), 2018, 37(5): 79-87. (in Chinese) DOI:10.16452/j.cnki.sdkjzk.2018.05.011 (  0) 0) |
| [7] |
Flores P, Ambrósio J, Claro J C P, et al. Spatial revolute joints with clearances for dynamic analysis of multi-body systems. Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics, 2006, 220(4): 257-271. DOI:10.1243/1464419JMBD70 (  0) 0) |
| [8] |
Tian Q, Zhang Y Q, Chen L P, et al. Dynamics of spatial flexible multibody systems with clearance and lubricated spherical joints. Computers and Structures, 2009, 87(13-14): 913-929. DOI:10.1016/j.compstruc.2009.03.006 (  0) 0) |
| [9] |
Wang G Q, Liu H Z. Dynamic response of crank-rod of an IC engine with clearance. Transactions of the Chinese Society of Agricultural Machinery, 2001, 32(6): 5-7. (  0) 0) |
| [10] |
Erkaya S, Dogan S, Sefkatlıoglu E. Analysis of the joint clearance effects on a compliant spatial mechanism. Mechanism and Machine Theory, 2016, 104: 255-273. DOI:10.1016/j.mechmachtheory.2016.06.009 (  0) 0) |
| [11] |
Pratiher B, Dwivedy S K. Nonlinear response of a flexible Cartesian manipulator with payload and pulsating axial force. Nonlinear Dynamics, 2009, 57(1-2): 177-195. DOI:10.1007/s11071-008-9431-6 (  0) 0) |
| [12] |
Li F C, Hou T T, Jia X J. Modeling and control of space manipulators considering joint clearance and gravity. Chinese High Technology Letters, 2015, 25(6): 599-606. DOI:10.3772/j.issn.1002-0470.2015.06.008 (  0) 0) |
| [13] |
Liu X F, Li H Q, Wang J S, et al. Dynamics analysis of flexible space robot with joint friction. Aerospace Science and Technology, 2015, 47: 164-176. DOI:10.1016/j.ast.2015.09.030 (  0) 0) |
| [14] |
Flores P, Koshy C S, Lankarani H M, et al. Numerical and experimental investigation on multibody systems with revolute clearance joints. Nonlinear Dynamics, 2011, 65(4): 383-398. DOI:10.1007/s11071-010-9899-8 (  0) 0) |
| [15] |
Bai Z F, Sun Y. A study on dynamics of planar multibody mechanical systems with multiple revolute clearance joints. European Journal of Mechanics - A/Solids, 2016, 60: 95-111. DOI:10.1016/j.euromechsol.2016.06.009 (  0) 0) |
| [16] |
Xu B C, Wang X P, Ji X M, et al. Dynamic and motion consistency analysis for a planar parallel mechanism with revolute dry clearance joints. Journal of Mechanical Science & Technology, 2017, 31(7): 3199-3209. DOI:10.1007/s12206-017-0609-z (  0) 0) |
| [17] |
Varedi-Koulaei S M, Daniali H M, Farajtabar M. The effects of joint clearance on the dynamics of the 3RRR planar parallel manipulator. Robotica, 2017, 35(6): 1223-1242. DOI:10.1017/S0263574715001095 (  0) 0) |
| [18] |
Zhang X C, Zhang X M. Minimizing the influence of revolute joint clearance using the planar redundantly actuated mechanism. Robotics and Computer-Integrated Manufacturing, 2017, 46: 104-113. DOI:10.1016/j.rcim.2017.01.006 (  0) 0) |
| [19] |
Chen G L, Wang H, Lin Z Q. A unified approach to the accuracy analysis of planar parallel manipulators both with input uncertainties and joint clearance. Mechanism & Machine Theory, 2013, 64(6): 1-17. DOI:10.1016/j.mechmachtheory.2013.01.005 (  0) 0) |
| [20] |
Zhang X C, Zhang X M, Chen Z. Dynamic analysis of a 3-RRR parallel mechanism with multiple clearance joints. Mechanism and Machine Theory, 2014, 78(78): 105-115. DOI:10.1016/j.mechmachtheory.2014.03.005 (  0) 0) |
| [21] |
Chen X L, Wu L K, Deng Y. Dynamic response and nonlinear characteristics of spatial parallel mechanism with spherical clearance joint. Journal of Computational and Nonlinear Dynamics, 2019, 14(4): 041010. DOI:10.1007/s11071-016-3191-5 (  0) 0) |
| [22] |
Xu L X, Li Y G. Investigation of joint clearance effects on the dynamic performance of a planar 2-DOF pick-and-place parallel manipulator. Robotics & Computer Integrated Manufacturing, 2014, 30(1): 62-73. DOI:10.1016/j.rcim.2013.09.002 (  0) 0) |
| [23] |
Wang X P, Liu G, Ma S J, et al. Effects of restitution coefficient and material characteristics on dynamic response of planar multi-body systems with revolute clearance joint. Journal of Mechanical Science and Technology, 2017, 31(2): 587-597. DOI:10.1007/s12206-017-0111-7 (  0) 0) |
| [24] |
Pennestrì E, Rossi V, Salvini P, et al. Review and comparison of dry friction force models. Nonlinear Dynamics, 2015, 83(4): 1785-1801. DOI:10.1007/s11071-015-2485-3 (  0) 0) |
| [25] |
Ambrósio J A C. Impact of rigid and flexible multibody systems: deformation description and contact models. Virtual Nonlinear Multibody Systems, 2003, 103: 57-81. DOI:10.1007/978-94-010-0203-5_4 (  0) 0) |
| [26] |
Flores P, Machado M, Seabra E, et al. A parametric study on the baumgarte stabilization method for forward dynamics of constrained multibody systems. Journal of Computational and Nonlinear Dynamics, 2011, 6: 011019-1. DOI:10.1115/1.4002338 (  0) 0) |
| [27] |
Liu F X, Wu C Y, Sun L. Analysis and test of influence of revolute joint clearance on performance of crank-rocker style transplanting mechanism. Transactions of the Chinese Society of Agricultural Engineering, 2016, 32(15): 9-17. DOI:10.11975/j.issn.1002-6819.2016.15.002 (  0) 0) |
 2021, Vol. 28
2021, Vol. 28


