Digital circuits' exponential scaling has led to a wide range of variation in process and design factors, causing performance uncertainty at the nanoscale technology node. Since the perfect control of photolithography and dopant quantity is difficult, process variations occur due to changes in threshold voltages and effective channel length. When both inter- and intra- die components are taken into account, effective channel length and threshold voltage can vary by up to 30% and 10%, respectively[1-2]. Process parameters, including isolation oxide strain, transistor orientation, and etch loading impact, further alter their nominal values. These parameters have been expressed statistically using appropriate distribution functions due to the stochastic character of the process changes and modelling challenges[2-4]. For example, the Gaussian distribution function is commonly employed. But because supply voltages and temperatures are unknown, they are generally regarded as corner parameters rather than random parameters. As the supply voltage is reduced to save energy, the sensitivity of delay parameters increases, and the supply voltage must be accurately evaluated in systems that handle parameter fluctuation[5-6]. In order to accommodate process variances in submicron circuit design, a delayed timing corner has been historically used to ensure all dies running at their maximum working frequency. Due to the increased variability in circuit delay at the ultra-deep submicron technology node, the minimum and maximum limitations for delay routes must be increased (i.e., the time calculated between the target obtained and the performance of the after-fabrication system). This technique may waste design resources as the number of process variables increases. To address this constraint, current research focuses on conveying the variance in gate delay across channels and identifying the probable solution of timing margins acquired[5-7]. Although the aforementioned strategies attempt to forecast minimal and maximum limits in the presence of statistical noise, their performance is dependent on the modelled fundamental gate delay variability and connection latency. MOSFET models, which serve as the basic correspondence vehicle between circuit designers and silicon foundries, play a critical part in chip outline efficiency. Although BSIM4[8] models for SPICE are well known to precisely model MOSFET, these are too complex to be used for analytical circuit design methodologies. Thus, precise physics-based efficient models that transform process parameter variation into delay variability at the circuit level are necessary for first-hand performance estimation. An analytical model capable of developing a methodology for optimum design needs to have the following features:
1) It should be small and capable of delivering analytic solutions to circuit equations for the fundamental digital building elements that make up the system's architecture.
2) A first order short channel effect should be included in the model equation to estimate the ON drain saturation current that defines the conducting state of the MOSFET switch[9-10].
3) In scaled MOSFETs of nanometer dimension, dimensional and process variability become an integral part of design consideration. In other words, the capability to handle variability for a statistical design is an added requirement of the analytical model[11-12].
4) The model must be able to handle designs that fall into both the high performance and low power categories. To meet the current standards for digital design, it is necessary that the model be relevant for both strong and moderate inversion zones.
5) The model should not only be scalable but also predictive, allowing for early design performance evaluation at new technology nodes around channel length limitations of 10 -20 nm[13-16].
6) The parameters of the analytical model should ideally match the parameters of the compact model used for circuit simulation. This allows the hand calculation or optimized paper design generated prior to SPICE to be effortlessly transferred to industry standard circuit simulators for silicon design prototype. Additionally, such a connection aids in the understanding of simulation data. Taking the above points into consideration, the following methodology has been adopted to derive the statical model:
a) The first step in the derivation is to update the first order velocity-field relationship with the three fitting parameters a, b, and c in order to translate the accuracy of the second order hyperbolic function to the first order velocity-field relationship. The amount of time spent on analytical computations is significantly decreased as a result of this.
b) The drain current expression now includes the impacts of secondary short channel effects such as parasitic resistance and DIBL.
c) For the purpose of enabling predictions of circuit performance for future technology generations, the proposed model is linked with the simple mathematical expressions of the Sakurai-Newton α-power law model[17] and the Predictive Technology Model (PTM)[18].
d) The physical value of α is found by equating the saturation drain current equation obtained from the proposed model with the saturation drain current equation acquired from the SN model. In order to scale down the physical value of α to a technology node as small as 32 nm, the PTM parameters are used.
e) In order to determine delay and its variability with changes in channel length and threshold voltage, the estimated drain current was used in conjunction with the channel length and threshold voltage estimates. The variations in channel length and threshold voltage have a substantial influence on the unpredictability of circuit delay.
f) The variability analysis was performed on the benchmark circuits ISCAS85[19] and Microelectronics Center of North Carolina (MCNC)[20]. Comparison of the mean and standard deviation obtained from the analytical findings with those obtained from Monte Carlo simulations revealed that the analytical results obtained are in close proximity with that of MC simulations.
1 Process VariationIntrinsic and extrinsic factors contribute to process variation. Intrinsic differences are often caused by device physics limits, while extrinsic variations are produced by manufacturing faults that vary by foundry. While extrinsic differences may be minimized via improved process control, intrinsic variations are uncontrollable and serve as a significant barrier to device scalability. Significant causes of intrinsic variation include the following:
1) Random dopant fluctuation: It has been shown in the literature that the quantity and location of dopant atoms implanted are random in nature at a scaled technology node. Due to the extremely small number of dopant atoms in scaled devices, there is a significant fluctuation in the threshold voltage (which is a function of dopant concentration). When the dopant atoms are large, the Poisson distribution may be used to estimate the dopant fluctuations, as opposed to the Gaussian distribution[21-22].
2) Roughness of the line edge: This refers to the variance in the form of the gate along the channel width direction. It happens more often near the mask borders, where bigger material grains dissolve more readily than smaller material grains. The roughness of the line edge does not scale with technology and cannot be decreased via lithographic process control. However, this has an effect on the threshold voltage and leakage current of the device[23-24].
3) Oxide thickness fluctuations: When the oxide layer thickness is a few Si atom layers, the atomic scale roughness at the interface of Si-SiO2 and gate SiO2 produces oxide thickness variations in scaled devices. This has an effect on the carrier mobility, and therefore on the device's threshold voltage[25-26].
All of the above-mentioned fluctuations become more significant as the technology node reduces, but random dopant fluctuations (which result in threshold variation) become increasingly crucial as the supply voltage drops. Because the variation in drain current is asymmetric at the ultra-deep submicron channel length and at lower supply voltage, statistical metrics like mean and standard deviation cannot be used to identify the shape of the distribution[27-28]. Thus, the probability distribution of drain current was studied using Skewness, a measure of asymmetry. Fig. 1 illustrates the skewness of MOSFET's current distribution with regard to supply voltage. The findings were acquired using a Monte Carlo simulation with 20000 HSPICE nodes at the 32 nm technology node. As the supply voltage drops, the drain current varies asymmetrically owing to the change in threshold voltage, which is considerably greater than that at higher supply voltage.
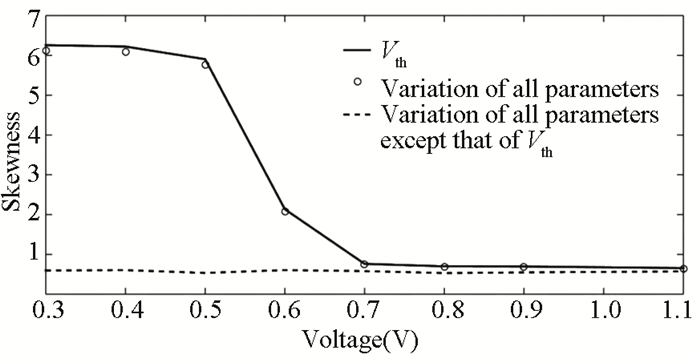
|
Fig.1 Drain current skewness at various supply voltages for 32 nm technology node |
In general, the variability of any random variable may be expressed as its standard deviation normalized by its mean (σ/μ) value, which indicates its global deviation.
2 Analysis of Circuit Performance VariabilityIn the past, Monte Carlo simulation of circuits has been used to study gate delay variability. Although the results are relevant, implementing them is time-consuming in practice. An alternative strategy is to implement the circuit using Response Surface Model (RSM), which raises the performance of the circuit linearly at nominal process values. Analysis of principal component technique is often used in addition to this technique to explore the various sources of statistical variation. Though this technique is only applicable to small channel transistors, the correlation between the parameters involved is quite complicated and non-linear, specifically the threshold voltage, which depends on the length of the channel. Additionally, utilizing the above two approaches (RSM and Monte Carlo), one can get only limited physical insights for improving circuit designs that are aware of variance. This paper presents an analytical modelling approach that is generalized for digital circuits and efficiently links the process variables to performance parameters. Thus, the presented model is a desirable choice for accurately and effectively forecasting delay variations at the circuit level. In order to extend the study of scalability of variability, the present model incorporates key physical phenomena that are seen at the ultra-deep sub-micron level. At any point x across the length of the channel, the drain current can be expressed as[29]
| $ I_{\mathrm{ds}}=I(x)=W C_{\mathrm{ox}}(\mathrm{VG}-n V(x)) v(x) $ | (1) |
In the above equation, W represents channel width, Cox represents capacitance of gate oxide computed per unit area, VG = Vgs -Vth, VG represents gate overdrive voltage, Vgs represents gate to source voltage, Vth represents threshold voltage, n represents bulk charge variation across the effective channel length, V(x) is potential in between minority charge quasi fermi potential as well as the bulk equilibrium fermi potential at point x, and v(x) represents carrier velocity computed at point x. The relationship between carrier velocity and the channel electric field in the inversion layer is described as
| $ v(E)=\frac{\mu_{\mathrm{eff}} E}{\left[1+\left(\frac{E}{E_{\mathrm{c}}}\right)^M\right]^{\frac{1}{M}}} $ | (2a) |
| $ E_{\mathrm{c}}=\frac{v_{\text {sat }}}{\mu_{\text {eff }}} $ | (2b) |
where E represents lateral electric field, μeff represents effective mobility, Ec is critical field measured when the carriers become velocity saturated, M is an empirical constant, M = 2 for negative charge carriers and M=1 for positive charge carriers, υsat represents saturation velocity measured in m/s. Since M=2 requires complex calculations[30], the following equation presents the modified first order υ-E model. Here, M=1 and a, b, c are the fitting constants described as
| $ v(E) = \frac{{a{\mu _{{\rm{eff}}}}E}}{{\left[ {b + c\left( {\frac{E}{{{E_{\rm{c}}}}}} \right)} \right]}} $ | (3a) |
| $ E_{\mathrm{c}}=\frac{b+c}{a} \cdot \frac{v_{\text {sat }}}{\mu_{\text {eff }}} $ | (3b) |
The three fitting parameters a, b, c are utilized to map first order hyperbolic function to second order. By doing so, the analytical calculations involved are reduced to a large extent. μeff is a function of the gate voltage and is expressed by[31-32]
| $ \mu_{\mathrm{eff}}=\frac{\mu_0}{1+\theta\left(V_{\mathrm{gs}}-V_{\mathrm{th}}\right)} $ | (4) |
where μ0 represents low field mobility, and θ is mobility degradation coefficient.
θm is the mobility degradation in the presence of parasitic resistance Rs, which can be expressed as[33]
| $ \theta_{\mathrm{m}}=\theta+\beta_0 R_{\mathrm{s}} $ | (5) |
where β0 represents maximum device transconductance. E(x) can be written by substituting Eq. (3) in Eq. (1):
| $ E(x)=\frac{I_{\mathrm{ds}} b}{W \mu_{\mathrm{eff}} C_{\mathrm{ox}} a(\mathrm{VG}-n V(x))-\frac{I_{\mathrm{ds}} c}{E_{\mathrm{c}}}} $ | (6) |
For obtaining the drain current of linear region, Eq. (6) is integrated from x=0 to x=L and V(x)=0 to V(x)=Vds. Here, L denotes effective channel length. Thus, The drain current of linear region can be expressed as
| $ I_{\mathrm{dlin}}=\frac{W a \mu_{\mathrm{eff}} C_{\mathrm{ox}}\left(\mathrm{VG}-n \frac{V_{\mathrm{ds}}}{2}\right) V_{\mathrm{ds}}}{L\left(b+\frac{c V_{\mathrm{ds}}}{E_{\mathrm{c}} L}\right)} $ | (7) |
It is well known that when the lateral electric field across the channel E(x) becomes equal to the value of critical electric field Ec, the carrier velocity saturates. Thus, putting E(x) =Ec in Eq. (6):
| $ I_{\mathrm{dsat}}=\frac{E_{\mathrm{c}} W \mu_{\mathrm{eff}} a C_{\mathrm{ox}}\left(\mathrm{VG}-n V_{\mathrm{dsat}}\right)}{b+c} $ | (8) |
where Vdsat represents drain saturation parameter.
Equating Eq. (7) and Eq. (8) that represent drain current in linear and saturation regions respectively, there is
| $ V_{\mathrm{dsat}}^2 \frac{n(c-b)}{2}+V_{\mathrm{dsat}} b\left(\mathrm{VG}+n E_{\mathrm{c}} L\right)-E_{\mathrm{c}} \mathrm{VG} L b=0 $ | (9) |
Roots of Eq. (9) are
| $ V_{\mathrm{dat}}=\frac{-b\left(\mathrm{VG}+n E_{\mathrm{c}} L\right)+\sqrt{\left(b\left(\mathrm{VG}+n E_{\mathrm{c}} L\right)\right)^2-2 n(c-b)\left(E_{\mathrm{c}} \mathrm{VG}Lb\right)}}{n(c-b)+\zeta} $ | (10) |
where the factor ζ has been introduced to avoid any instability in the mathematical computation. The value of ζ is finitely very small. The above equation describes Vdsat effectively and has been utilized to solve short channel drain current expressions.
In the presence of parasitic source/drain resistance Rs, Idsat is expressed as
| $ I_{\mathrm{dsat}}=\frac{I_{\mathrm{dsat} 0}}{1+\frac{R_{\mathrm{s}} I_{\mathrm{dsat} 0}}{V_{\mathrm{gs}}-V_{\mathrm{th}}}} $ | (11) |
where Idsat0 =Idsat for Rs = 0.
The parasitic resistance is an important factor at ultra-deep submicron technology node. Thus, it has been included in all the calculations done further utilizing α-power calculations to obtain appropriate accuracy and prediction[29].
Another short channel effect reliant in deep submicron technology node is drain induced barrier lowering (DIBL). The effect of change in threshold voltage in the presence of DIBL can be modeled as[29]
| $ V_{\text {th }}\left(V_{\mathrm{ds}}\right)=V_{\mathrm{th}}-\sigma_{\text {DIBL }} V_{\mathrm{ds}}=V_{\text {th }}-\delta V_{\text {th }} $ | (12) |
where Vth represents threshold voltage at low Vds (0.1V) or nominal value of Vds in Eq. (12), δVth represents difference in the threshold voltage measured at higher Vds, δVth=Vth-Vth Vds, σDIBL is DIBL parameter.
α-power Law MOSFET Model is the most frequently used model for short channel devices because of its high degree of accuracy and simplicity. In this paper, the physical proposed model is linked to α-power model[17]. The following equations of drain current are developed by Sakurai and Newton (SN) and commonly known as α-power MOSFET model:
| $ I_{\mathrm{dsat}}=\frac{W}{L} B\left(V_{\mathrm{gs}}-V_{\mathrm{th}}\right)^\alpha\left(1+\lambda V_{\mathrm{ds}}\right) $ | (13) |
| $ I_{\mathrm{dlin}}=\frac{W}{L} B\left(V_{\mathrm{gs}}-V_{\mathrm{th}}\right)^\alpha\left(2-\frac{V_{\mathrm{ds}}}{V_{\mathrm{dsat}}}\right) \frac{V_{\mathrm{ds}}}{V_{\mathrm{dsat}}} $ | (14) |
| $ V_{\mathrm{dsat}}=V_{\mathrm{dsat} 1}\left(\frac{V_{\mathrm{gs}}-V_{\mathrm{th}}}{V_{\mathrm{dd}}-V_{\mathrm{th}}}\right)^{0.5 \alpha} $ | (15) |
| $ V_{\mathrm{dsat} 1}=V_{\mathrm{dsat}} \mid V_{\mathrm{gs}}=V_{\mathrm{dd}} $ | (16) |
where α represents velocity saturation index, B represents transconductance parameter, λ represents channel length modulation parameter, Vdd represents the supply voltage.
The logarithm graphs' outstanding linearity demonstrates the correctness of
| $ I_{\mathrm{dsat}}=B\left(V_{\mathrm{gs}}-V_{\mathrm{th}}\right)^\alpha $ | (17) |
Ref. [34] incorporates the width effect and suggests the following changes in the established SN-model for the current equations in the linear and saturation region:
| $ I_{\mathrm{dsat}}=K_1\left(V_{\mathrm{gs}}-V_{\mathrm{th}}\right)^\alpha\left(1+\lambda V_{\mathrm{ds}}\right) $ | (18) |
| $ I_{\mathrm{dlin}}=K_1\left(V_{\mathrm{gs}}-V_{\mathrm{th}}\right)^\alpha\left(2-\frac{V_{\mathrm{ds}}}{V_{\mathrm{dsat}}}\right) \frac{V_{\mathrm{ds}}}{V_{\mathrm{dsat}}} $ | (19) |
Parameter B in the SN mode was updated to factor K1 and accounts for width effect.
| $ K_1=\beta_1+\beta_2 W+\beta_3 W^2 $ | (20) |
where β1, β2 and β3 are fitting coefficients.
Thus, neglecting λ in Eq. (18), the saturation drain current can be written as
| $ I_{\mathrm{dsat}}=K_1\left(V_{\mathrm{gs}}-V_{\text {th }}\right)^\alpha $ | (21) |
The value of K1 can be calculated by substituting log(Vgs -Vth) = 0. Thus, putting VG=1 in Eq. (8),
| $ K_1=\frac{E_{\mathrm{c}} W \mu_{\mathrm{eff}} a C_{\mathrm{ox}}\left(1-n V_{\mathrm{dsat}}\right)}{b+c} $ | (22) |
The physical value of α may be determined by putting Idsat (Eq. (22)) = (Eq. (8)):
| $ K_1\left(V_{\mathrm{gs}}-V_{\mathrm{zh}}\right)^\alpha=\frac{E_{\mathrm{c}} W \mu_{\mathrm{eff}} a C_{\mathrm{ox}}\left(\mathrm{VG}-n V_{\mathrm{dsat}}\right)}{b+c} $ | (23) |
where Vdsat is given by Eq. (10). Thus,
| $ \alpha=\frac{\ln \frac{E_{\mathrm{c}} W \mu_{\mathrm{eff}} a C_{\mathrm{ox}}\left(\mathrm{VG}-n V_{\mathrm{dsat}}\right)}{K_1(b+c)}}{\ln \left(V_{\mathrm{gs}}-V_{\mathrm{th}}\right)} $ | (24) |
The physical values of α obtained for different technology nodes are summarized in the Table 1. It is worth noting that the value of threshold voltage obtained from α-power model and the analytical model is not the same. Thus, the threshold voltage is repeatedly iterated with the starting value as given in PTM model[18] till the error obtained reaches less than 2% for the entire voltage range.
| Table 1 Model parameters utilized for calculations |
The model equations presented above are applicable in strong inversion region. But for low power circuit applications, where the circuit is operating in either weak or moderate inversion region, modification to the industry standard EKV equation[35] is proposed. The EKV model describes the drain current applicable in all regions of operations for long channel devices as
| $ i_{\mathrm{ds}}=\ln ^2\left(1+\exp \frac{\left(v_{\mathrm{gs}}-v_{\mathrm{th}}\right)}{2}\right) $ | (25) |
where
| $ \begin{gathered} i_{\mathrm{ds}}=I_{\mathrm{ds}} / I_{\mathrm{spec}} \\ v_{\mathrm{gs}}=V_{\mathrm{gs}} / U_{\mathrm{T}} \\ v_{\mathrm{th}}=V_{\mathrm{th}} / U_{\mathrm{T}} \\ U_{\mathrm{T}}=K T / q \\ I_{\mathrm{spec}}=2 n \mu C_{\mathrm{ox}} U_{\mathrm{T}}^2 W / L \end{gathered} $ |
where Ids, Ispec, UT, T, q represent unnormalized drain current, specific current, thermal voltage, temperature and unit charge respectively.
For transistor working in moderate or weak operating regions, the following is the proposed modification model:
| $ i_{\mathrm{ds}}=\ln ^\alpha\left(1+\exp \frac{\left(v_{\mathrm{gs}}-v_{\mathrm{th}}\right)}{2}\right) $ | (26) |
The value of α can be found through mathematical interpolation with the same procedure as described by Ref. [35].
3 Gate Delay VariabilityThe time delay of the CMOS inverter is calculated based on the length of time it takes to charge or discharge the load capacitance during operation. The delay of propagation (tp) of a gate can be represented as[36-40]
| $ t_{\mathrm{p}}=\frac{C_{\mathrm{L}} V_{\mathrm{dd}}}{I_{\mathrm{ON}}} $ | (27) |
where CL is the output load capacitance, ION is the ON current of MOSFET or drain when Vgs=Vds=Vdd.
| $ I_{\mathrm{ON}}=K_1\left(V_{\mathrm{dd}}-V_{\mathrm{th}}\right)^\alpha $ | (28) |
Output load capacitance is defined as the amount of intrinsic capacitance of the fan-out gates from the driving phase and is denoted by CL. As a result, CL is proportional to
| $ C_{\mathrm{L}} \propto C_{\mathrm{ox}} L\left(\xi_i W_i+W_{i+1}\right) $ | (29) |
ξi refers to the relationship between parasitic capacitance in the driver stage and input gate capacitance in the fanout stage. i-th and (i+1)-th are the driver and load stage annotations, respectively. W becomes Wi in Eq. (27) (transconductance factor K1 is also width dependent as expressed in Eq. (20)). Putting CL value from Eq. (29) into the given Eq. (27), there is
| $ t_{\mathrm{p}}=\frac{V_{\mathrm{dd}} C_{\mathrm{ox}} L\left(\xi_i W_i+W_{i+1}\right)}{\left(\beta_1+\beta_2 W_i+\beta_3 W_i^2\right)\left(V_{\mathrm{dd}}-V_{\mathrm{th}}\right)^\alpha} $ | (30) |
For N numbers of stages across the pathway, the path delay (PD) can be estimated as the total of gate delays. Thus,
| $ \begin{array}{r} \mathrm{PD}=\frac{V_{\mathrm{dd}} C_{\mathrm{ox}} L\left(\xi_i W_i+W_{i+1}\right)}{\left(V_{\mathrm{dd}}-V_{\mathrm{th}}\right)^\alpha} \cdot \\ \sum\limits_{i=1}^N \frac{\xi_i W_i+W_{i+1}}{\left(\beta_1+\beta_2 W_i+\beta_3 W_i^2\right)} \end{array} $ | (31) |
| $ \mathrm{PD}=k_{\mathrm{pd}} V_{\mathrm{dd}} \mathrm{PD}(W) $ | (32) |
where kpd is the technology-dependent factor, and PD(W) depends on the size of the transistor that makes gate sizing along the path. Historically, delay for N stages has been expressed in terms of the average single-stage propagation delay tp and the logic depth Ld. Logic depth is defined as the greatest number of fundamental logic gates that a signal may travel from source to destination in any digital circuit, PD = tpLd, but this formulation does not allow the sizing of the gate.
The gate delay given in Eq. (27) is used to investigate variability by accounting for variations in threshold voltage caused by DIBL and in specific current caused by mobility degradation. If the statistical variation in effective channel length and threshold voltage is considered to be Gaussian and there is a high correlation between transistors with small range of gate size, the variability in gate delay (σ/μ, coefficient of variation) is stated as follows:
| $ \frac{\sigma_{\mathrm{t}}}{t_{\mathrm{p}}}=\sqrt{\left(\frac{\delta \ln t_{\mathrm{p}}}{\delta L}\right)^2 \sigma_L^2+\left(\frac{\delta \ln t_{\mathrm{p}}}{\delta V_{\mathrm{th}}}\right)^2 \sigma_{V_{\mathrm{th}}}^2} $ | (33) |
where
If the circuit is extremely big and spatial correlation dependency cannot be ignored, it can be split into smaller sub-circuits and then the variability of the partitioned sub-circuits can be computed as described below.
The process parameters are stated as a sum of correlated and random components, and the total of the variances of these two components yields the process parameter's overall variation.
Correlated variations are addressed by dividing the larger circuit as a grid and representing the variation in each square of the grid with a single random variable. To simplify the problem, the set of coupled random variables was substituted with another set of mutually independent random variables with zero mean and unit variance using principal component analysis. It is to be noted that the correlation structure of process parameters is often specified by a distance-dependent function. Using such a function to create the correlation matrix may result in non-positive-definite correlation matrices. Simple approaches, such as ignoring the correlation matrix's negative eigenvalues, may be utilized to overcome such concerns[41]. The single gate delay is presented as follows:
| $ \text { Delay }=d_{\text {norm }}+\sum\limits_{i=1}^q \alpha_{\mathrm{q}}\left(\Delta P_{\mathrm{q}}\right) $ | (34) |
where dnorm is the nominal value of delay expressed by Eq. (30), αq represents sensitivity of delay to process parameters under consideration and, ΔPq is the change in the process parameters from their nominal value. For each timing arc associated with the gate, the values of dnorm and αq are determined and stored in a two-dimensional database indexed by the input transition time and output load capacitance. After partitioning the big circuit with a grid, the delay of individual gates is stated as a function of the grid's random variables. The delay in Eq. (34) is then stated as using the principal component technique described as
| $ \text { Delay }=d_{\text {norm }}+\sum\limits_{i=1}^q\left(\alpha_{\mathrm{q}} \sum\limits_{j=1}^n \gamma_{j i} z_j\right)+\eta_{\mathrm{d}} R $ | (35) |
where zj is the principal component of the corelated random variable ΔPq in Eq. (34) and γji can be determined using principal component analysis. R simulates random variants with a specified normal distribution. (R~N(0, 1)) in Eq. (35) denotes the random component of all process parameter fluctuations combined into a single term that contributes a total variance of ηd2 to the overall delay variance.
The delay of each gate (Da) can therefore be expressed as
| $ D_a=a_0+\sum\limits_{i=1}^n a_i z_i+a_{n+1} R $ | (36) |
The above expression is a canonical delay expression. The nominal delay (a0) is the mean delay. Since, zi are uncorrelated N(0, 1) random variable, the delay variance can be expressed as
| $ \operatorname{Var}\left(D_a\right)=\sum\limits_{i=1}^n a_i^2+a_{n+1}^2 $ | (37) |
The covariance of delay with one of the principal components can be expressed as
| $ \begin{array}{l} {\mathop{\rm Cov}\nolimits} \left( {{D_a}, {z_i}} \right) = E\left( {{D_a}, {z_i}} \right) - E\left( {{D_a}} \right)E\left( {{z_i}} \right) = a_i^2\\ \;\;\;\;\;\;\;\;\forall \in 1, 2, \cdots , n \end{array} $ | (38) |
Due to the fact that the random components are uncorrelated and hence do not contribute to the covariance of the delay at the two nodes corresponding to the gate's inputs (example "a" and "b"), the covariance may be calculated as
| $ \operatorname{Cov}\left(D_a, D_b\right)=\sum\limits_{i=1}^n a_i b_i $ | (39) |
The delay of the circuit is determined in deterministic timing analysis by applying two functions on the delay of individual gates: sum and max. Similar functions are defined as follows for the delay expression given in Eq. (36):
| $ \begin{aligned} &\operatorname{Sum}\left(D_a, D_b\right)=\left(a_0+b_0\right)+\sum\limits_{i=1}^n a_i+ \\ &b_i z_i+\sqrt{a_{n+1}^2+b_{n+1}^2} R \end{aligned} $ | (40) |
The maximum function is not strictly Gaussian for normally distributed random variables. According to Refs. [42-43], the maximum of two Gaussian random variables may be approximated highly accurately by another Gaussian. If
| $ c=\max (a, b) $ | (41) |
where a and b are Gaussian random variables, the parameter c, which is assumed to be Gaussian, may be calculated using the formulas presented in Ref. [44]. This method calculates the mean and variance of c in terms of the means and variances of a and b, as well as their correlation coefficients. Additionally, Ref. [44] creates equations for evaluating the correlation between c and any other random variable in terms of the random variable's connection with a and b. It is supposed that, in accordance with Refs. [42] and [45], c may be stated in the same canonical form as a and b. To get the coefficients for the canonical form expression for c, the mean, variance, and correlation of c with the main components are matched, resulting in the following expression:
| $ \begin{gathered} c_0=E(\max (a, b)) \\ c_i=\operatorname{Cov}\left(c, z_i\right)=\operatorname{Cov}\left(\max (a, b), z_i\right) \forall \in 1, 2, \cdots, n \\ c_{n+1}=\left(\operatorname{Var}(\max (a, b))-\sum\limits_{i=1}^n c_i^2\right)^{1 / 2} \end{gathered} $ | (42) |
It is possible to preserve the mean and variance of the random component while avoiding scaling the correlation coefficients of the primary components to match the variance, which would result in a loss of their correlation in the space between them[42]. Additionally, Ref. [45] employs this method to account for random changes in timing analyses. The aforementioned approach is employed iteratively to find the maximum of more than two variables.
4 Model Validation1) The suggested model represented in Eq. (30) has been validated for a variety of supply voltages as well as various threshold voltages as shown in Fig. 2 to ensure that it is accurate, where Vth0 represents zero bias threshold voltage. From the image, it can be observed that the suggested model accurately predicts delays for voltages above and below the threshold voltages used in the experiment. It was necessary to verify the acquired findings using the industry standard HSPICE while taking the PTM[18] model into consideration. For the validation of this model, an error in the range of 1%-10% is considered acceptable for inaccuracy.
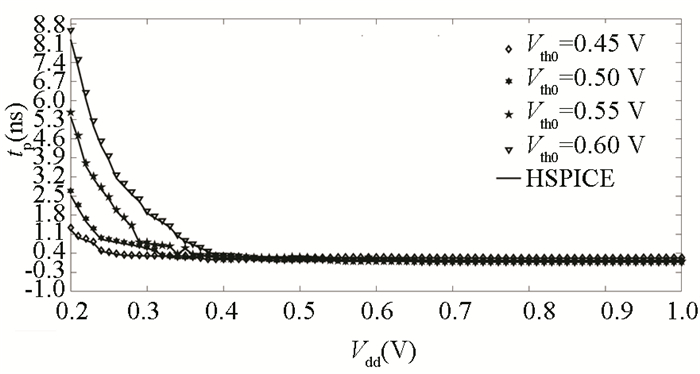
|
Fig.2 Relationship between the CMOS inverter gate delay with FO4 load with Vdd and L and Vth (32 nm) |
2) Using the suggested model expressed in Eq. (30), the delay of the CMOS inverter is further tested throughout a wide range of L and supply voltage Vdd. The result of this verification is illustrated in Fig. 3 for the 32 nm technology node. As can be seen in the image, the suggested model is verified over a broad range of channel length variations (up to 40% of the total channel length). Using the industry standard HSPICE and PTM model[18], it was required to confirm the data that had been obtained. For the purposes of validating this model, an obtained error in the range of 1%-10% is deemed acceptable in terms of inaccuracy.
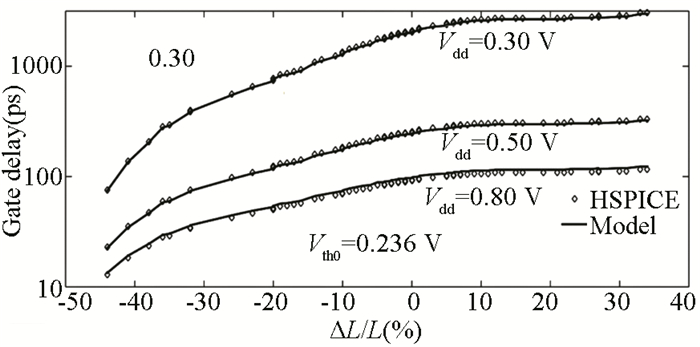
|
Fig.3 Relationship between nominal delay and L (32 nm) |
3) The variability of the CMOS inverter is displayed in Fig. 4 by adjusting the threshold voltage L and Vth solely, the channel length only, and varying both at various supply voltages, with Monte Carlo circuit simulations, assuming L and Vth fluctuations are normally distributed and the variability expression from Eq. (33). On the basis of the figure, it can be concluded that channel length differences account for around 60% of delay variations. Therefore, this proposed analytical method may be utilized for first hand investigations of delay variability. Slower gate delays are more variable at lower power supplies due to nonlinear gate delay response. Eq. (1) in Ref. [46] quantifies the trend, whereas our model accurately predicts it.
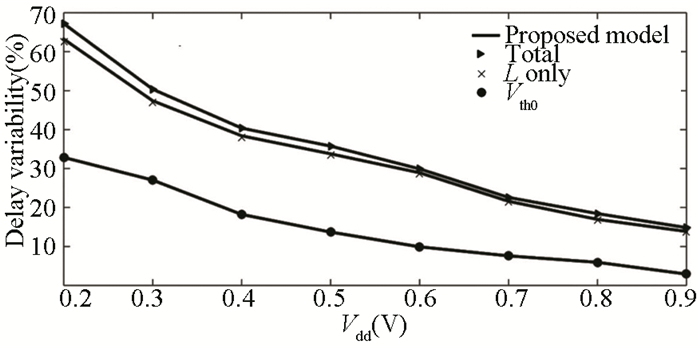
|
Fig.4 The proposed model that correctly predicts delay variability (32 nm) |
4) Further deconstruction of variability into causal physical processes is warranted given the relative importance of different sources of process variation, as indicated in Fig. 5 generated from the proposed model in Eq. (30) and presented in Fig. 5. It is obvious from the figure that threshold voltage variations caused by DIBL are the primary source of the problem, particularly at lower supply voltages. However, the transconductance factor, which takes into account the impacts of both size (W/L) and loading capacitance, is the primary source of variations in areas over the threshold. L contributes to these variations, which are essentially independent of supply voltage Vdd.

|
Fig.5 Individual physical processes' contribution to variable delay (32 nm) |
5) In Fig. 6, σt/tp represents the variation in delay time represented by the CMOS inverter with FO4 load (taking into account variation of both L and Vth and L), which is calculated from the variability expression provided in Eq. (33). A decrease in the variability σt/tp can be detected when the value of σ is normalized by the mean values of threshold voltage and effective channel length, as illustrated in Fig. 6. Assuming Vdd=0.6 V, their contributions are essentially identical between Vth and L. When the supply voltage is reduced, it can be observed that the change in normalized Vth is large when compared with the change in L, as seen in the figure. However, since the absolute variation of L is greater than that of the other variables, L continues to be the dominant source of variability.
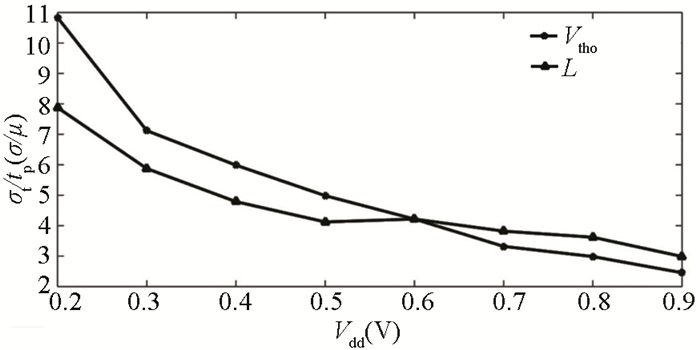
|
Fig.6 Sensitivity of the variation in delay due to variation in normalized effective channel length L and Vth |
6) Table 2 shows the findings for the ISCAS85[19] and Microelectronics Center of North Carolina (MCNC)[20] benchmark circuits, respectively. It is shown in the table how the mean and standard deviation of delay are acquired using the suggested model and compared with those obtained using MC-based simulations. Comparison of circuits with different logic depths shows that circuits with lower logic depths exhibit more variations in delay than circuits with higher logic depths. This is due to the fact that the correlations in the random component are not taken into account, which might result in an inaccuracy in the calculated variance. It is also found that the error in delay is inversely proportional to the depth of the critical path[15] and can be expected to be small for larger circuits.
| Table 2 Comparison of the proposed model with MC simulations |
5 Conclusions
This paper presented an analytical model of delay variability that is physically grounded and suitable for pre-SPICE analysis. The model incorporates short channel effects of DIBL and velocity saturation and is accurate over a broad variety of supply voltage Vdd, including sub-threshold. The relative significance of Vth and L variation in terms of total digital circuit delay variability has been demonstrated and the model was used to explain the underlying physical phenomena. The obtained results lie within the acceptable range of 1%-10%.
| [1] |
Lorenz J, Bär E, Barraud S, et al. Process variability-Technological challenge and design issue for nanoscale devices. Micromachines, 2018, 10(1): 6. DOI:10.3390/mi10010006 (  0) 0) |
| [2] |
Wang X S, Adamu-Lema F, Cheng B J, et al. Geometry, temperature, and body bias dependence of statistical variability in 20-nm bulk CMOS technology: a comprehensive simulation analysis. IEEE Transactions on Electron Devices, 2013, 60(5): 1547-1554. DOI:10.1109/TED.2013.2254490 (  0) 0) |
| [3] |
Wang R S, Yu T, Huang R, et al. Impacts of short-channel effects on the random threshold voltage variation in nanoscale transistors. Science China Information Sciences, 2013, 56(6): 062403. DOI:10.1007/s11432-013-4814-9 (  0) 0) |
| [4] |
Kim Y B. Challenges for nanoscale MOSFETs and emerging nanoelectronics. Transactions on Electrical and Electronic Materials, 2010, 11(3): 93-105. DOI:10.4313/TEEM.2010.11.3.093 (  0) 0) |
| [5] |
Guerrieri S D, Bonani F, Ghione G. Modeling techniques for electronic noise and process variability in nanoscale devices. Proceedings of the 2018 IEEE 13th Nanotechnology Materials and Devices Conference (NMDC). Piscataway: IEEE, 2018. 18401805. DOI: 10.1109/NMDC.2018.8605838.
(  0) 0) |
| [6] |
Jooypa H, Dideban D. Impact analysis of statistical variability on the accuracy of a propagation delay time compact model in nano-CMOS technology. Journal of Computational Electronics, 2018, 17(1): 192-204. DOI:10.1007/s10825-017-1108-2 (  0) 0) |
| [7] |
Lü W F, Sun L L. Compact modeling of response time and random-dopant-fluctuation-induced variability in nanoscale CMOS inverter. Microelectronics Journal, 2014, 45(6): 678-682. DOI:10.1016/j.mejo.2014.03.019 (  0) 0) |
| [8] |
Liu W D, Jin X D, Cao K M, et al. BSIM4.1.0 MOSFET Model: User's Manual. Berkeley: University of California, 2000. 31-50
(  0) 0) |
| [9] |
Gildenblat G. Compact Modeling: Principles, Techniques and Applications. New York: Springer-Verlag, 2010: v-vi.
(  0) 0) |
| [10] |
Grabinski W, Nauwelaers B, Schreurs D. Transistor Level Modeling for Analog/RF IC Design. New York: Springer, 2006: ix-xiii.
(  0) 0) |
| [11] |
Saha S K. Compact MOSFET modeling for process variability aware VLSI circuit design. IEEE Access, 2014, 2: 104-115. DOI:10.1109/ACCESS.2014.2304568 (  0) 0) |
| [12] |
Jooypa H, Dideban D. Statistical strategies to reproduce the propagation delay time variability using compact models. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2019, 66(11): 1880-1884. DOI:10.1109/TCSⅡ.2019.2895364 (  0) 0) |
| [13] |
Nanoscale Integration and Modeling (NIMO) Group. Predictive Technology Model. http://ptm.asu.edu/, 2022-03-01.
(  0) 0) |
| [14] |
Klös A, Kostka A. PREDICTMOS - a predictive compact model of small-geometry MOSFETs for circuit simulation and device scaling calculations. Solid-State Electronics, 2000, 44(7): 1145-1156. DOI:10.1016/S0038-1101(00)00045-9 (  0) 0) |
| [15] |
Khakifirooz A, Antoniadis D A. MOSFET performance scaling Part Ⅰ: historical trends. IEEE Transactions on Electron Devices, 2008, 55(6): 1391-1400. DOI:10.1109/TED.2008.921017 (  0) 0) |
| [16] |
Khakifirooz A, Antoniadis D A. MOSFET performance scaling-Part Ⅱ: future directions. IEEE Transactions on Electron Devices, 2008, 55(6): 1401-1408. DOI:10.1109/TED.2008.921026 (  0) 0) |
| [17] |
Sakurai T, Newton R. α-power law MOSFET model and its applications to CMOS inverter delay and other formulas. IEEE Journal of Solid-State Circuits, 1990, 25(2): 584-594. DOI:10.1109/ICCAD.1988.122466 (  0) 0) |
| [18] |
Cao Y. Predictive technology model of conventional CMOS devices. Chandrakasan A. Integrated Circuits and Systems. Boston: Springer, 2011: 7-23. DOI:10.1007/978-1-4614-0445-3
(  0) 0) |
| [19] |
Brglez F. A neural netlist of 10 combinational benchmark circuits. Proceedings of the IEEE ISCAS: Special Session on ATPG and Fault Simulation. Piscataway: IEEE, 1985. 151-158.
(  0) 0) |
| [20] |
Yang S. Logic Synthesis and Optimization Benchmarks User Guide. Version 3.0. Microelectronics Center of North Carolina (MCNC), 1991.
(  0) 0) |
| [21] |
Dash T. P, Jena J, Mohapatra E, et al. Role of stress/strain mapping and random dopant fluctuation in advanced CMOS process technology nodes. International Journal of Nano and Biomaterials, 2020, 91(1-2): 18-33. DOI:10.1504/IJNBM.2020.10029632 (  0) 0) |
| [22] |
Zhang K, Lu W F, Si P, et al. Suppression of timing variations due to random dopant fluctuation by back-gate bias in a nanometer CMOS inverter. Recent Advances in Electrical and Electronic Engineering (Formerly Recent Patents on Electrical & Electronic Engineering), 2021, 14(3): 339-346. DOI:10.2174/2352096513666201208102615 (  0) 0) |
| [23] |
Jha C K, Gupta C, Gupta A, et al. Impact of LER on mismatch in nanosheet transistors for 5nm-CMOS. Proceedings of the 2020 4th IEEE Electron Devices Technology and Manufacturing Conference (EDTM). Piscataway: IEEE, 2014. 1-4. DOI: 10.1109/EDTM47692.2020.9117816.
(  0) 0) |
| [24] |
Shin C. Line edge roughness (LER). Shin C. Variation Aware Advanced CMOS Devices and SRAM. Dordrecht: Springer, 2016: 19-35.
(  0) 0) |
| [25] |
Yang F L, Hwang J R, Li Y M. Electrical characteristic fluctuations in sub-45nm CMOS devices. Proceedings of the IEEE Custom Integrated Circuits Conference. Piscataway: IEEE, 2006. 691-694. DOI: 10.1109/CICC.2006.320881.
(  0) 0) |
| [26] |
Kuhn K, Kenyon C, Kornfeld A, et al. Managing process variation in Intel's 45nm CMOS technology. Intel Technology Journal, 2008, 12(2): 93-109. (  0) 0) |
| [27] |
Okada K, Kento Y, Onodera H. A statistical gate-delay model considering intra-gate variability. Proceedings of the International Conference on Computer Aided Design 2003. Piscataway: IEEE, 2003. 908-913. DOI: 10.1109/ICCAD.2003.159782.
(  0) 0) |
| [28] |
Harish B P, Bhat N, Patil M B. On a generalized framework for modeling the effects of process variations on circuit delay performance using response surface methodology. IEEE Transactions on Computer-aided Design of Integrated Circuits and Systems, 2007, 26(3): 606-614. DOI:10.1109/TCAD.2006.883910 (  0) 0) |
| [29] |
Narain N. Mosfet Modeling for VLSI Simulation: Theory and Practice. Singapore: World Scientific, 2007: 235-242.
(  0) 0) |
| [30] |
Taylor G W. Velocity-saturated characteristics of short channel MOSFETs. AT&T Bell Laboratories Technical Journal, 1984, 63(7): 1325-1404. DOI:10.1002/j.1538-7305.1984.tb00039.x (  0) 0) |
| [31] |
Yeric G M, Tasch A F, Banerjee S K. A universal MOSFET mobility degradation model for circuit simulation. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 1990, 9(10): 1123-1126. DOI:10.1109/43.62736 (  0) 0) |
| [32] |
Agostinelli V M, Yeric G M, Tasch A F. Universal MOSFET hole mobility degradation models for circuit simulation. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 1993, 12(3): 439-445. DOI:10.1109/43.215005 (  0) 0) |
| [33] |
Kiddee K, Ruangphanit A, Niemcharoen S, et al. Extraction of mobility degradation, effective channel length and total series resistance of NMOS at elevated temperature. Proceedings of the 8th Electrical Engineering/ Electronics, Computer, Telecommunications and Information Technology (ECTI) Association of Thailand-Conference 2011. Piscataway: IEEE, 2011. 1-4. DOI: 10.1109/ECTICON.2011.5947755.
(  0) 0) |
| [34] |
Chandra N, Yati A K, Bhattacharyya A B. Extended-Sakurai-Newton MOSFET model for ultradeep-submicrometer CMOS digital design. Proceedings of the 2009 22nd International Conference on VLSI Design. Piscataway: IEEE, 2009. 247-252. DOI: 10.1109/VLSI.Design.2009.48
(  0) 0) |
| [35] |
Enz C C, Vittoz E A. Charge-based MOS Transistor Modeling: the EKV Model for Low-power and RF IC Design. Hoboken, New Jersey: John Wiley & Sons, 2006. 41-45. DOI: 10.1002/0470855460.
(  0) 0) |
| [36] |
Markovi D, Wang C C, Alarcon L P, et al. Ultralow-power design in near-threshold region. Proceedings of the IEEE, 2010, 98(2): 237-252. DOI:10.1109/JPROC.2009.2035453 (  0) 0) |
| [37] |
Kalra S, Bhattacharyya A B. Scalable α-power law based MOSFET model for characterization of ultra deep submicron digital integrated circuit design. AEU-International Journal of Electronics and Communications, 2018, 83: 180-187. DOI:10.1016/j.aeue.2017.08.029 (  0) 0) |
| [38] |
Kalra S, Bhattacharyya A B. Ultra low power design for digital CMOS circuits operating near threshold. International Journal of Electronics and Telecommunications, 2017, 63(4): 369-374. DOI:10.1515/eletel-2017-0050 (  0) 0) |
| [39] |
Kalra S, Bhattacharyya A B. An analytical study of temperature dependence of scaled CMOS digital circuits using a-power MOSFET model. Journal of Integrated Circuits and Systems, 2016, 11(1): 57-68. DOI:10.29292/jics.v11i1.430 (  0) 0) |
| [40] |
Kalra S. Effect of temperature dependence on performance of digital CMOS circuit technologies. Proceedings of the 2013 International Conference on Signal Processing and Communication. Piscataway: IEEE, 2013. 392-395. DOI: 10.1109/ICSPCom.2013.6719819.
(  0) 0) |
| [41] |
Xiong J, Zolotov V, He L. Robust extraction of spatial correlation. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2006, 26(4): 619-631. DOI:10.1109/TCAD.2006.884403 (  0) 0) |
| [42] |
Chang H L, Sapatnekar S S. Statistical timing analysis considering spatial correlations using a single PERT-like traversal. Proceedings of the International Conference on Computer Aided Design 2003. Piscataway: IEEE, 2003. 621-625. DOI: 10.1109/ICCAD.2003.159746.
(  0) 0) |
| [43] |
Tsukiyama S, Tanaka M, Fukui M. A new statistical static timing analyzer considering correlations between delays. Proceedings of the ACM Workshop on Timing Issues in the Specification and Synthesis of Digital Systems (TAU). New York: ACM, 2000. 27-33.
(  0) 0) |
| [44] |
Clark C E. The greatest of a finite set of random variables. Operations Research, 1961, 9(2): 145-291. DOI:10.1287/opre.9.2.145 (  0) 0) |
| [45] |
Viswesweriah C, Ravindran K, Kalafala K, et al. First-order incremental block-based statistical timing analysis. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2005, 25(10): 331-336. DOI:10.1109/TCAD.2005.862751 (  0) 0) |
| [46] |
Eisele M, Berthold J, Schmitt-Landsiedel D, et al. The impact of intra-die device parameter variations on path delays and on the design for yield of low voltage digital circuits. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 1997, 5(4): 360-368. DOI:10.1109/92.645062 (  0) 0) |
 2022, Vol. 29
2022, Vol. 29


