2. Beijing E-hualu Information Technology Co. Ltd., Beijing 100043, China;
3. Chengdu Civil Aviation Information Technology Co. Ltd., Chengdu 610041, China
As the civil aviation transport industry has continuously and rapidly developed, the number of flights has increased rapidly, and the apron business has become increasingly busy. This has constantly brought a greater demand for ground service support. In most airports, the bottleneck of inefficient scene operations and insufficient coordination capacities has become more prominent, which does not allow support vehicles to arrive on time and causes flight delays. Thus, delays in ground service support are one of the main reasons for flight delays. Relevant statistics indicate that delays caused by ground service support account for 15.45% of all delays in large hub airports[1]. Solving the scheduling problem of support vehicles and creating more efficient support operations has become a key component of research in airport management. In a hub airport, the takeoff and landing of flights are characterized by short-term high density, which easily forms a flight wave. The flight wave makes the delay have network effect, i.e., the delay will spread along with the flight and difficultly eliminate in a short time. The goal of support vehicles scheduling is to avoid flight delay caused by ground service support as far as possible, and to allocate support vehicles as reasonably as possible, so as to improve support operations.
Throughout the world, research on vehicle scheduling problems for airport ground service support has focused primarily on two solutions[2]. The first method is expert systems that add scheduling rules to the knowledge base system[3]. The second method is mathematical programming for modeling[4]. The progress of computer technology has enabled various optimization algorithms to effectively solve complex programming problems, which has led to the mathematical programming method being widely applied. As such, there have been promising relevant research results in recent years. Kuhn and Loth[5] built a mixed-integer linear programming model to describe the vehicle scheduling problem and solved the problem quickly using the genetic algorithm. Norin et al.[6] proposed an adaptive search algorithm based on greedy randomness to solve the scheduling problem of deicing vehicles. Padron et al.[7] scheduled different types of support vehicles and developed a global scheduling scheme by solving the dual-objective optimization problem. Heng and Wang[8] built an agent model of support vehicles and designed a dynamic programming algorithm based on Petri net. Qin[9] designed a branch construction algorithm by optimizing the support operation process.
However, there are few researches on the scheduling problem of support vehicles. Flight scheduling is similar to vehicle scheduling in airport ground service support, which has a significant amount of relevant research results.Mattias[10] built a constraint programming model for flight scheduling based on the column generation method. Gabteni and Grönkvist[11] used the hybrid column generation method and constraint programming algorithm to solve the problem of flight scheduling. Lieder et al.[12] classified aircraft into classes and solved the scheduling problem based on these classes using a heuristic algorithm. Inspired by the scheduling algorithm of railways, Godbole et al.[13] proposed a branch-and-bound global-search algorithm to solve the optimization problem of aircraft ground movement under uncertain time constraints. Marcella et al.[14] used a special algorithm based on mixed-integer linear programming to solve the flight scheduling problem during busy hours. Scheduling models established by most scholars mainly optimize objectives from the perspectives of airports, airlines and passengers, including objective functions such as least delayed flights, highest efficiency and minimum waiting time. However, giving full play to the capability of ground service support should not be ignored, i.e., the machine-hours of support vehicles should be balanced.
The vehicle scheduling problem in airport ground service support is a parallel and time-window-limited optimization problem with multiple objectives, which belongs to the class of non-deterministic polynomial-time hard (NP-hard) problems. There are two kinds of algorithms used to solve NP-hard problems: precise and heuristic. Precise algorithms have a relatively low solving capability, and it is difficult to obtain an exact solution when the problem is complex. In contrast, heuristic algorithms have a high efficiency, and a relatively satisfactory solution can be obtained after a small number of calculations[15]. Common heuristic algorithms include the C-W saving algorithm[16], Soloman insertion algorithm[17], tabu search algorithm[18], simulated annealing algorithm[19], and genetic algorithm[20]. Compared with other heuristic algorithms, the ant colony algorithm has the characteristics of self-organization, a parallel solving process, positive feedback mechanism, and strong robustness[21], w'hich has advantages and feasibility to solve NP-hard problems. An improved ant colony algorithm is proposed to solve the scheduling problem of support vehicles, and its capabilities and effectiveness are analyzed.
1 Methods 1.1 Topology Model of Operational AreaThe operational area for ground service support in airports can be divided into several smaller zones, such as the gate position. For ground service support operations, small zones generate support demand at a specified moment. The operational role of ground service support includes a variety of support vehicles, which transfer through the roads between each small zone to meet the support demand distribution over different spatial positions. Graph theory is used to build a topology model for the operational area to visually represent the spatial relationships between each small zone in the operational area and the connecting road and to store and process the relevant information more efficiently.
The topology model for the support area includes three elements: operation zone, nodes, and roads. A schematic diagram of the topology is shown in Fig. 1. The operation zone refers to the specific region where support operations are completed in the operational area, such as the gate position and baggage handling hall. The node refers to the virtual node that connects the operation zone and the road, which corresponds to the individual operation zones. This can be regarded as a subset of the operation zone and the endpoint of a road. The road is for support vehicles to drive on, which is generally undirected, and each has an associated weight.

|
Fig.1 Schematic diagram of the topology model |
The driving time is used as the weight of the road, which is the quotient of the length of the road to the average speed, and the adjacency matrix W is used to store the driving time for each road. As there are n nodes, W=(Wij)n×n where Wij=0. If a road connects nodes i to j, then Wij=(driving time)ij, where (driving time)ij is the driving time associated with the road. If there is no road from node i to j, then Wij=∞.
In practice, it is necessary to determine the shortest driving time between any two nodes in the operational area to achieve the highest transfer efficiency for support vehicles. The shortest driving time matrix L can be obtained from the Floyd shortest path algorithm based on the matrix W. The algorithm executes as follows:
Step 0 Initialization, let k=0, L=W;
Step 1 Let i=0, if k ≤ n, then k=k+1; otherwise, end the algorithm and output L;
Step 2 Let j=0, if i≤n, then i=i+1; otherwise, return to Step 1;
Step 3 If j ≤n, then j=j+1; otherwise, return to Step 2;
Step 4 Calculate Lij using Eq.(1) and store Lij, then return to Step 3.
| $ L_{i j}=\min \left\{L_{i j}, L_{i k}+L_{k j}\right\} $ | (1) |
In large hub airports, there are more than10 types of support vehicles, such as refueling trucks, catering trucks, cleaning trucks, shuttle buses, and passenger ladder trucks. Some assumptions are made to uniformly describe the scheduling model of support vehicles. (1) The number of flights that demand the same support vehicles and support resources is determined only by the type of aircraft, which is the expected value. (2) Multiple support vehicles of the same type are not differentiated and will not break down during operations. (3) The time window to operate the support vehicles is fixed and unchangeable.
1) Related Parameters and Variables
The relevant parameters and variables for the vehicle scheduling model in airport ground service support are defined as follows:
i, j—serial number of the operation zones, including the aircraft stand, supply point, and loading and unloading point;
tM(i, j)—transfer time from operation zones i to j;
Z0—serial number of parking or supply points for support vehicles;
l—type of aircraft, l∈{C, D, E, F};
nl—number of support vehicles required for the type l aircraft;
k—serial number of flights (aircraft), k∈{1, 2, …, F}, where F is the maximum number of flights that need support;
lk—type of aircraft k;
ik—serial number of aircraft stand for aircraft k;
(ET) k, (LT)k—earliest start time and latest start time for the support operations of aircraft k, which together constitute the operating time window;
dk—delay time of flight k;
d—average delay time of delayed flights;
h—serial number of support vehicles, h∈{1, 2, …, U}, where U is the maximum number of support vehicles in the airport;
g, g, g0——aircrafts operated by a support vehicle on the same day, in which aircraft g is the previous aircraft of g and aircraft g0 is the first aircraft operated by the support vehicle on that day;
qh—machine-hours for support vehicle h;
qmax—maximum machine-hours for all support vehicles;
xhk—decision variable, which is 1 if aircraft k is operated by the support vehicle and is 0 otherwise;
SThk—start time of support operations by support vehicle h for aircraft k;
(tW)lk—support operating time for aircraft k, whose type is l.
2) Objective Functions and Constraints
The objective functions of the support vehicle scheduling model can be summarized as follows. The delay time of flights is minimized and the machine-hours of support vehicles are as balanced as possible. Minimizing the delay is the primary objective to avoid the situation where the delay time is not long but flight delays are widespread and where a small number of flights are delayed but the delay time is too long. This is manifest in two aspects: minimizing the number of delayed flights and minimizing the variance of delay. Due to the network effect of delay, minimizing the number of delayed flights should be taken as the primary objective function, followed by balancing the machine-hours of support vehicles and avoiding a small number of flights being delayed too long. The objective functions are shown in Eqs.(2)-(4).
| $ {\rm{min}}E_1=\sum\limits_{k=1}^F \operatorname{sign}\left(d_k\right) $ | (2) |
| $ {\rm{min}}E_2=\sqrt{\sum\limits_{h=1}^U\left(q_{\max }-q_h\right)^2} $ | (3) |
| $ {\rm{min}}E_3=\sqrt{\sum\limits_{k=1}^F \operatorname{sign}\left(d_k\right)\left(d_k-\bar{d}\right)^2} $ | (4) |
The constraints of the support vehicle scheduling model are shown in Eqs. (5)-(10). Eq. (5) ensures that the number of support vehicles operating for the same aircraft does not exceed its demand. Eq. (6) indicates that the start time of support operations should be within the time window. If a delay cannot be avoided, the constraint can be relaxed.
| $ \sum\limits_{h=1}^U x_{h k}=n_{l_k} $ | (5) |
| $ (\mathrm{ET})_k \leqslant \mathrm{ST}_{h k} \leqslant(\mathrm{LT})_k $ | (6) |
| $ \left\{\begin{array}{l} \mathrm{ST}_{h g^0}=(\mathrm{ET})_{g^0} \\ \mathrm{ST}_{h g}=\max \left\{\mathrm{ST}_{h g^{-}}+\left(t_{\mathrm{W}}\right)_{l_{g^{-}}}+t_{\mathrm{M}}\left(i_{g^{-}}, i_g\right), (\mathrm{ET})_g\right\} \end{array}\right. $ | (7) |
| $ d_k=\max \left\{\mathrm{ST}_{h k}-(\mathrm{LT})_k, 0\right\}, \bar{d}=\frac{\sum\limits_{k=1}^F d_k}{\sum\limits_{k=1}^F \operatorname{sign}\left(d_k\right)} $ | (8) |
| $ q_h=\sum\limits_{k=1}^F x_{h k} \cdot\left(t_{\mathrm{W}}\right)_{l_k}, q_{\max }=\max\limits_{h=1}^U\left\{q_h\right\} $ | (9) |
| $ x_{h k}=0, 1 ; \mathrm{ST}_{h k}>0 ; d_k \geqslant 0 ; q_h>0 ; \forall h, k $ | (10) |
3) Limited Support Vehicle Capacity
Some types of support vehicles, such as catering trucks, have a limited capacity. When the support resources carried are insufficient, the vehicle must return to the supply point to replenish. Therefore, an objective function (shown in Eq. (11)) should be added to the support vehicle scheduling model to minimize the trips of support vehicles to the supply point to make full use of the resources. In addition, constraints (shown in Eqs. (12) and (13)) should be added, and Eq. (7) should be modified as Eq. (14). Eq. (12) indicates that a support vehicle must meet the demand for support resources of a flight.
| $ {\rm{min}}E_4=\sum\limits_{h=1}^U \sum\limits_{k=1}^F \operatorname{sign}\left(y_{h k}\right) $ | (11) |
| $ r_{h k} \geqslant R_{l_k} $ | (12) |
| $ r_{h g}=y_{h g} \cdot r_0+\left(1-y_{h g}\right)\left(r_{h g^{-}}-R_{l_g-}\right), r_{h g^0}=r_0 $ | (13) |
| $ \left\{\begin{aligned} & \mathrm{ST}_{h g^0}=(\mathrm{ET})_{g^0} \\ & \mathrm{ST}_{h g}= \max \left\{\mathrm{ST}_{h g^{-}}+\left(t_{\mathrm{W}}\right)_{l_{g^{-}}}+y_{h g}\left[t_M\left(i_{g^{-}}, Z_0\right)+t_{\mathrm{CS}}+\right.\right. \\ &\left.\left.\;\;\;\;\;\;\;\;\;t_{\mathrm{M}}\left(Z_0, i_g\right)\right]+\left(1-y_{h g}\right) \cdot t_{\mathrm{M}}\left(i_{g^{-}}, i_g\right), (E T)_g\right\} \end{aligned}\right. $ | (14) |
where yhk is the decision variable valued at 1 if support vehicle h returns to the supply point before operating aircraft k and is 0 otherwise; rhk is the amount of residual support resources of support vehicle h before operating aircraft k; Rl is the demand for support resources for an aircraft of type l; r0 is the resource capacity of a capacity-limited support vehicle; and tCS is the resource replenishment time of a capacity-limited support vehicle.
1.3 Ant Colony Algorithm Based on Response ValueAnalyzing the mathematical model of the scheduling problem indicates that there is a constraint relationship between the start time of support operations, the operating time window, and the spatial distribution of aircraft stands. The start time directly affects the delay, and the machine-hours are directly determined by the scheduling scheme. If the responsiveness of each support vehicle to the current operational demand can be described from the start time, and support vehicles with a strong response capacity are assigned to the current operational demand first, then the efficiency of the algorithm to solve the scheduling model can be enhanced.
1) Response Value of Support Vehicle
Let the current time be T, the start time of the next support operation by a support vehicle be ST, the transfer time be tM, and the operating time window be [ET, LT]. According to Eqs. (6) and (7), the quantitative relation between variables is as shown in Eq. (15). Then, Eq. (16) is obtained after merging these expressions, which directly reflects the relationship between the current time, the transfer time, and the operating time window. Let the length of the operating time window be tTW=LT -ET, which provides Eq. (17) after insertion into Eq.(16). As shown in Eq. (17), if there are a support demand and some support vehicles on standby, then the value of (ET-T) is fixed. When given a value for tTW (tM), a larger (smaller) tM (tTW) indicates it is more likely that the constraint on the right side of Eq. (17) will not be satisfied. That is, an "unwilling" delay will be generated. Therefore, the response capability of support vehicles can be described using tM and tTW. The response value of support vehicles can be defined as shown in Eq. (18). Thus, it is advantageous to assign a support vehicle with a higher response value to the support demand.
| $ \mathrm{ST}=T+t_{\mathrm{M}}, \mathrm{ET} \leqslant \mathrm{ST} \leqslant \mathrm{LT} $ | (15) |
| $ \mathrm{ET} \leqslant T+t_{\mathrm{M}} \leqslant \mathrm{LT} $ | (16) |
| $ 0 \leqslant \frac{t_{\mathrm{M}}-(\mathrm{ET}-T)}{t_{\mathrm{TW}}} \leqslant 1 $ | (17) |
| $ c=\frac{t_{\mathrm{TW}}}{t_{\mathrm{M}}} $ | (18) |
The response value for a capacity-limited support vehicle should be 0 when support resources are insufficient. Let the number of current support resources of the vehicle be r, and the demand for support resources of the next aircraft be R. Then, the response value of the vehicle is calculated from Eq. (19).
| $ c=a \frac{t_{\mathrm{TW}}}{t_{\mathrm{M}}} $ | (19) |
where a is the parameter valued at 1 if r < R and is 0 otherwise.
2) Ant Controller
The ant foraging process needs to be improved according to the timing of arrival/departure flights and the number of available support vehicles. The ant foraging process will cycle many times where the number of cycles equals the number of support vehicles. During foraging, the ants select foraging sites in turn based on the transfer rules, and the selected foraging sites are placed into a tabu list. When no foraging site can be selected, the ant instantly returns to the nest and begins the next foraging process, which begins from the foraging sites that were never placed in the tabu list. The foraging sites of the final foraging process are all the remaining sites. When the foraging process of one ant is complete, a feasible solution is output based on the tabu list. The tabu list is then cleared, and the next ant begins foraging. When all ants have finished foraging, the pheromone distribution is updated based on the pheromone update rules, and the next iteration begins. When the objective value converges or reaches the maximum number of iterations, the algorithm is complete and the optimal solution is output.
The ant controller can record the current time, position, and amount of residual support resources to determine whether the ant needs to return to the nest. When the ant sets out from the nest, T=0 and r=r0. When the ant is at the foraging site k, the value of T and r are respectively updated by Eqs. (20) and (21).
| $ T=\mathrm{ST}_{h k}+\left(t_{\mathrm{W}}\right)_{l_k} $ | (20) |
| $ r=r^{-}-R_{l_k} $ | (21) |
where r- is the value of r when the ant is at the last foraging site.
The ant returns to the nest when r is less than Rlk for all remaining foraging sites as the support resources are insufficient. Then, T is updated from Eq. (22) and r is reset to r0. When T is greater than (LT)k for all remaining foraging sites (which can be relaxed by Eq. (23) based on the actual situation), there are no foraging sites that can be chosen and the ant returns to the nest. Then, T is reset to 0 and r is reset to r0.
| $ T=\mathrm{ST}_{h k}+\left(t_{\mathrm{W}}\right)_{l_k}+t_{\mathrm{M}}\left(i_k, Z_0\right)+t_{\mathrm{cs}} $ | (22) |
| $ T>(\mathrm{LT})_k+d_{\text {allow }} $ | (23) |
where dallow is the maximum delay allowed for flights.
3) Transfer Rules
There are two primary factors considered when selecting the next foraging site: pheromone concentration and response value. The pheromone concentration determines the global optimization ability of ants and the local optimization ability is dictated by the response value. When an ant is at the foraging sitek, its response value to the foraging site k′ is ckk′. Then, the probability that the ant transfers from foraging site k to k′ is as shown in Eq. (24), and the ant randomly selects the next foraging site based on its probability distribution. The α reflects the relative role of the accumulated pheromone concentration in the foraging process where a greater value indicates the ants are more likely to be attracted by the previous foraging process. The β reflects the relative role of the deterministic factors where a greater value indicates a higher efficiency for the current foraging path. Excessive values of α and β will reduce the randomness of the foraging process and prematurely lead to a local optimum; thus, there is a strong coupling between them[22]. The values of α and β should be determined by the actual problem, and the methods to determine them mainly include setting by experience, setting experimentally, and optimization using algorithms[23]. According to the results from the reference by Chen[24], using α=1 and β=2-5 gives good effects.
| $ P_{k k^{\prime}}= \begin{cases}\frac{\left(\tau_{k k^{\prime}}\right)^\alpha\left(c_{k k^{\prime}}\right)^\beta}{\sum\limits_{k^{\prime} \in {\mathit{\Omega}}(k)}\left(\tau_{k k^{\prime}}\right)^\alpha\left(c_{k k^{\prime}}\right)^\beta}, & k^{\prime} \in {\mathit{\Omega}}(k) \\ 0, & k^{\prime} \notin {\mathit{\Omega}}(k)\end{cases} $ | (24) |
where Ω(k) is the collection of all remaining foraging sites, τkk′ is the pheromone concentration between foraging site k and k′, α is the heuristic factor of the pheromone, and β is the heuristic factor of the responsiveness.
4) Tabu List
The tabu list records the foraging path of the ants while outputting the results and calculating the machine-hours of each support vehicle, as shown in Table 1. The location of the nest is numbered as 0, and each foraging path starts from the nest and is recorded in turn. The support operating time of the nest is 0, and the machine-hours are calculated when completing a foraging path. The transfer path between two adjacent foraging sites constitutes the collection of the foraging paths.
| Table 1 Tabu list from the ant foraging algorithm |
5) Pheromone Update Rules
As time progresses, the original pheromones in the foraging path gradually evaporate, and the ants will leave new pheromones along the foraging path. The ant-cycle model is adopted to update thepheromone distribution in real-time. According to the degree of importance, the objective functions (Eqs. (2)-(4)) are combined to a comprehensive objective function (Eq. (25)) in which δ1 = 0.4 and δ2 = δ3 = 0.3 are desired.
| $ {\rm{min}}E_5=\left[\sum\limits_{k=1}^F \operatorname{sign}\left(d_k\right)\right]^{\delta_1} \cdot\\ \left[\sqrt{\sum\limits_{h=1}^U\left(q_{\max }-q_h\right)^2}\right]^{\delta_2}\left[\sqrt{\sum\limits_{k=1}^F \operatorname{sign}\left(d_k\right)\left(d_k-\bar{d}\right)^2}\right]^{\delta_3} $ | (25) |
where δ1, δ2, and δ3 are the importance factors that satisfy δ1 + δ2 + δ3 = 1.
In the Nth iteration, the pheromone concentration between foraging sites k and k′ is τkk′(N), which can be calculated from Eqs. (26) and (27). The τkk′(N) consists of the remaining pheromones and newly added pheromones from the (N - 1)th iteration. The newly added pheromones are left by ants in the foraging path with an optimal comprehensive objective function.
| $ \left\{\begin{array}{l} \tau_{k k^{\prime}}(1)=1 \\ \tau_{k k^{\prime}}(N)=\rho \cdot \tau_{k k^{\prime}}(N-1)+\Delta \tau_{k k^{\prime}}(N-1) \end{array}\right. $ | (26) |
| $ \Delta \tau_{k k^{\prime}}(N-1)=\left\{\begin{array}{l} \frac{Q}{F}, k-k^{\prime} \in \partial(N-1) \\ 0, k-k^{\prime} \notin \partial(N-1) \end{array}\right. $ | (27) |
where ρ is the pheromone residual coefficient, which usually takes ρ=0.5-0.8; Δτkk′(N-1) is the newly added pheromones; Q is the number of pheromones that ants leave behind during foraging; k-k′ is the transfer path from foraging sites k to k′; and ∂(N-1) is the collection of foraging paths with an optimal comprehensive objective function.
6) Algorithm Steps
Set the number of ants to mmax and the maximum number of iterations to Nmax. Then, the steps of the improved ant colony algorithm are (visually shown in Fig. 2):

|
Fig.2 Flow chart of the algorithm |
Step 0 Initialization, import relevant data, and let N=0;
Step 1 If the optimal objective value has converged, or N>Nmax, output the optimal solution and end the algorithm; otherwise, N=N+1. Let m=0, place all ants in the nest, and empty the current optimal objective value and current optimal solution;
Step 2 If m>mmax, update the pheromone concentration on the foraging path based on the current optimal solution and return to Step 1; otherwise, m=m+1. Let h=0, place all foraging sites into the collection of the remaining foraging sites, and empty the tabu list;
Step 3 For ant m, let T=0, i=Z0, and r=r0. If h=U-1, jump to Step 5; otherwise, h=h+1;
Step 4 The ant randomly selects the next foraging site k from the collection of remaining foraging sites based on the probability distribution after respectively calculating and storing SThk and dk, and the foraging site k is placed in the tabu list. At the same time, foraging site k is removed from the collection of remaining foraging sites, and the values of T, i, and r are updated, based on which it is determined whether the ant goes back to the nest. If a foraging path is completed, qh is calculated and placed into the tabu list. Then, return to Step 3; otherwise, repeat Step 4;
Step 5 h=U, the ant selects the remaining foraging sites from the collection. After completing foraging path U, the comprehensive objective function is calculated using Eq. (25). If the current comprehensive objective value is better, replace the current optimal objective value with it. At the same time, replace the current optimal solution with the current feasible solution and jump to Step 6; otherwise, return to Step 2;
Step 6 If the current optimal objective value is better, replace the optimal objective value with it and replace the optimal solution with the current optimal solution. Then return to Step 2; otherwise, directly return to Step 2.
2 Case StudyThe ant colony algorithm (ACO) based on the response value is applied to the scheduling of refueling trucks in an airport as a case study. There are three refueling trucks in Terminal 1 of a hub airport in China, all of which have pipelines and do not carry jet fuel. A total of 96 flights took off from this terminal on a certain day, and the time distribution of the flights is shown in Fig. 3. As seen from the time distribution trend of departure flights (red line), there are roughly two peak periods in the day, one from 02:00 to 06:00 and one from 12:00 to 14:00.
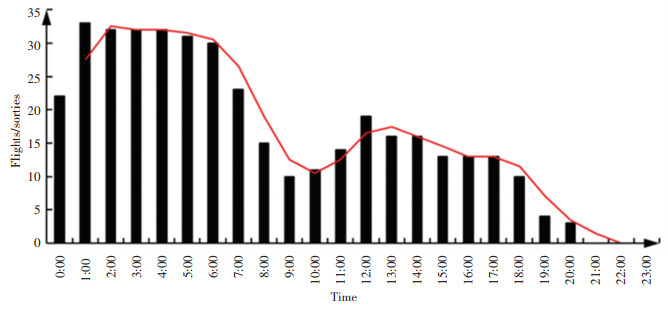
|
Fig.3 Time distribution of departure flights |
The topology model of Terminal 1 is shown in Fig. 4, where there are 28 operation zones (yellow squares), nodes (blue circles) and roads (red lines). Specifically, zone 0 is the garage of refueling trucks. The relevant flight data sets were collected and processed, and the flight demand data for refueling operations were collected, which were sorted based on the earliest start time. Some representative data are shown in Table 2.
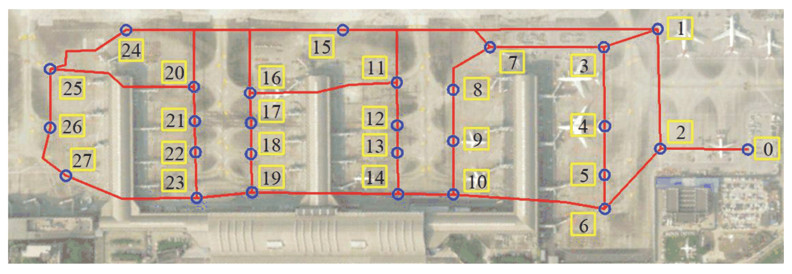
|
Fig.4 The topology model of Terminal 1 |
| Table 2 Demand data for refueling operations of some flights |
In addition to the method based on experience, the most commonly used algorithm is the first-come-first-served (FCFS) approach. The refueling truck scheduling method based on FCFS is as follows. A certain flight is assigned to a refueling truck that begins to operate the earliest. If all refueling trucks are occupied, the subsequent flights will have to queue for refueling operations. Thus, a scheduling scheme of refueling trucks on a day is obtained, as shown in Table 3.
| Table 3 Scheduling scheme of refueling trucks based on the FCFS |
The improved ACO is also used to schedule the refueling trucks. First, the flight demand data are imported for refueling operations to complete the initialization. Secondly, to more quickly converge the improved ACO, it begins from an initial solution before searching for the optimal solution. This takes the scheduling scheme of the refueling trucks based on FCFS as the initial solution and initializes the pheromone distribution from there. Then, the parameters of the improved ACO are set as follows: dallow is 15 min, α is 1.0, β is 2.0, ρ is 0.8, mmax is 75, Nmax is 200, and the iterations converge when the objective value occurs 30 times. Finally, the algorithm is run, and the results are output to obtain the scheduling scheme on the given day, as shown in Table 4.
| Table 4 Schedulingscheme of the refueling trucks based on the improved ACO |
3 Results
According to statistics from Travel Sky, the average delay of departing flights at the airport on that day was 64 min. As the delay caused by ground service support accounted for 15.45% of all delays, the delay caused by ground service support was calculated as 9.89 min.Based on the scheduling schemes from the FCFS and improved ACO, the delays caused by ground service support are 7.79 and 3.36 min, respectively. It is seen that refueling operations greatly impact the efficiency of ground service support. The delay caused by refueling operations accounts for 78.77% of the delay caused by ground service support, which occupies 12.17% of all delays. If the scheduling scheme based on the improved ACO was adopted, the delay caused by refueling operations would decrease by 56.87%.
The scheduling scheme based on the improved ACO can effectively reduce delays caused by refueling operations. Further, the objective and comprehensive objective values for the two scheduling schemes are calculated through Eqs.(2)-(4) and Eq.(25), respectively, as shown in Fig. 5. By comparison, it is concluded that in terms of each objective value, the scheduling scheme based on the improved ACO is superior to that for the FCFS. From the perspective of machine-hours, the scheduling scheme based on the improved ACO is particularly effective and can well balance the machine-hours of each refueling truck.
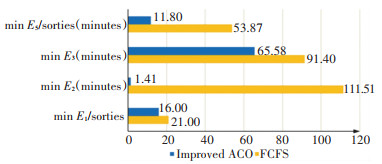
|
Fig.5 Comparison of the scheduling scheme for refueling trucks |
4 Discussion
The introduction of the response value for support vehicles is an innovation of the improved ACO to solve the scheduling problem. The effects of the improved ACO that considers the pheromone distribution only (ACO by information) with the ACO that considers the expected transfer time (ACO by expectation) are further analyzed through an application comparison.
First, the convergence ability of the improved ACO, ACO by information, and ACO by expectation are analyzed by comparing the current optimal objective values, as shown in Fig. 6. It is seen from the figure that the ACO by expectation has the fastest convergence speed and strongest optimization ability, but the worst random searching ability and falls into a local optimum prematurely with relatively large fluctuations. The ACO by information has the strongest random searching ability and the most stable searching process, but the worst optimization ability and the slowest convergence speed. The convergence speed, optimization ability, and random searching ability of the improved ACO are moderate, whose search process is also stable with the ability to jump out of local optima. The figure shows that the improved ACO jumps out of local optima twice, and a global optimum is reached for the first time. To summarize, introducing the response value of support vehicles allows the improved ACO to jump out of local optima and allows searching for the global solution, which is not available to the other approaches.

|
Fig.6 Comparison of the current optimal target convergence based on the optimization algorithms |
Second, the scheduling schemes from the three algorithms are compared, as shown in Fig. 7. It is concluded that the results obtained from the improved ACO are a good balance among the three approaches. The improved ACO can control the number of delayed flights and variance of delay at a lower level and is effective at balancing the machine-hours. Neither the ACO by information nor the ACO by expectation can achieve this same effect. The improved ACO maximizes the effects of balancing machine-hours for all support vehicles by introducing the response value, which makes full use of support resources, improves the operational efficiency of ground service support, and minimizes flight delays.
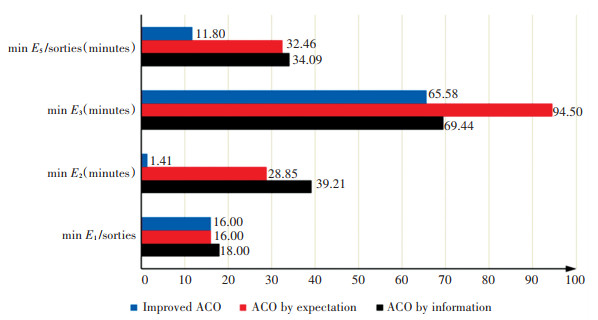
|
Fig.7 Comparison of refueling truck scheduling algorithms |
5 Conclusions
The major findings of this study are as follows. Graph theory was used to build the topology model of the operational area to realize the spatial representation of support operations for airport ground service, which provides a good basis for follow-up research.A scheduling model was built based on the characteristics of the scheduling problem with the objectives of reducing flight delays and balancing the machine-hours of support vehicles, where the time window and capacity limitations are the main constraints. This realizes the mathematical description of the vehicle scheduling problem for airport ground service support. The ant controller, transfer rules, tabu list, pheromone update rules, and algorithm steps are designed to improve the ant colony algorithm. The transfer rules were optimized with the response value of the support vehicle to provide a new concept to solve the NP-hard scheduling problem.
In the application, the delay caused by refueling operations using the scheduling scheme of the improved ACO was reduced by 56.87% compared with the FCFS, which indicates that the improved ACO achieves the expected effect. Compared with the ACO that considers the pheromone distribution only and the ACO that considers the expected transfer time, the improved ACO can jump out of local optima, which not only reduces delays but also balances the vehicle machine-hours. Thus, the response value can depict the responsiveness of support vehicles.
To simplify the scheduling problem, some idealized assumptions (such as the expected value of some parameters, ignoring individual differences in support vehicles, and fixed time windows) were made when building the mathematical model of the vehicle scheduling problem.For future work, the model should be improved accordingly due to the complexity of actual problems. In addition, the efficiency of using the Floyd shortest path algorithm and the adjacency matrix to calculate and store the shortest driving time will be greatly reduced when the support area is further expanded. The Floyd shortest path algorithm has high time complexity, which will become very inefficient when it is applied to the calculation of hundreds of nodes. Only by establishing a more professional airport ground geographic information system can this problem be fundamentally solved.
6 Data Availability StatementAs the dataset requires a large storage capacity, only part of the data is showed in this article. But the raw data can be provided by the authors if needed. Requests to access the dataset should be directed to hitwhofcy@163.com.
AcknowledgmentsThe authors sincerely thank all teachers and students who gave significant support to this paper.
| [1] |
Ma Z P, Cui D G. Optimizing airport flight delays. Journal of Tsinghua University (Science and Technology), 2004, 4: 474-477, 484. DOI:10.16511/j.cnki.qhdxxb.2004.04.011 (  0) 0) |
| [2] |
Gosling G D. Design of an expert system for aircraft gate assignment. Transport Research Part A: General, 1990, 24(1): 59-69. DOI:10.1016/0191-2607(90)90071-D (  0) 0) |
| [3] |
Su Y Y, Srihari K. A knowledge based aircraft gate assignment advisor. Computers and Industrial Engineering, 1993, 25(2): 123-126. DOI:10.1016/0360-8352(93)90236-Q (  0) 0) |
| [4] |
Babic O, Teodorovic D, Tosic V. Aircraft stand assignment to minimize walking. Journal of Transportation Engineering, 1984, 110(1): 55-66. DOI:10.1061/(ASCE)0733-947X(1984)110:1(55) (  0) 0) |
| [5] |
Kuhn K, Loth S. Airport service vehicle scheduling. Air Traffic Control Quarterly, 2010, 18(1): 63-83. DOI:10.2514/atcq.18.1.63 (  0) 0) |
| [6] |
Norin A, Yuan D, Granberg T A, et al. Scheduling de-icing vehicles within airport logistics: a heuristic algorithm and performance evaluation. Journal of the Operational Research Society, 2012, 63(8): 1116-1125. DOI:10.1057/jors.2011.100 (  0) 0) |
| [7] |
Padron S, Guimarans D, Ramos J J, et al. A bi-objective approach for scheduling ground-handling vehicles in airports. Computers & Operations Research, 2016, 71: 34-53. DOI:10.1016/j.cor.2015.12.010 (  0) 0) |
| [8] |
Heng H J, Wang F. Research on real-time scheduling of airport special vehicles based on MAS. Application Research of Computers, 2017, 34(9): 2599-2604. DOI:10.3969/j.issn.1001-3695.2017.09.008 (  0) 0) |
| [9] |
Qin S S. Research and Application of Branch Construction Algorithm for Flight Support Process. Xi′an: Xi′an Shiyou University, 2018. DOI: CNKI:CDMD:2.1018.210957.
(  0) 0) |
| [10] |
Mattias G. The Tail Assignment Problem. Gothenburg, Sweden: Chalmers University of Technology and University of Gothenburg, 2005. DOI: viewdoc/summary/10.1.1.103.825.
(  0) 0) |
| [11] |
Gabteni S, Grönkvist S. Combining column generation and constraint programming to solve the tail assignment problem. Annals of Operations Research, 2009, 171(1): 61-76. DOI:10.1007/s10479-008-0379-1 (  0) 0) |
| [12] |
Lieder A, Stolletz R, Briskorn D. An efficient optimization algorithm for the aircraft scheduling problem with aircraft classes. Pediatric Pulmonology, 2013, 44(5): 944. DOI:10.1002/ppul.21002 (  0) 0) |
| [13] |
Godbole P J, Ranade A G, Pant R S. Branch-and-bound global-search algorithm for aircraft ground movement optimization. Journal of Aerospace Computing, Information, and Communication, 2017, 14(6): 316-326. DOI:10.2514/1.I010344 (  0) 0) |
| [14] |
Marcella S, D'Ariano A, Palagachev K, et al. Integration methods for aircraft scheduling and trajectory optimization at a busy terminal maneuvering area. OR Spectrum, 2019, 41: 641-681. DOI:10.1007/s00291-019-00560-1 (  0) 0) |
| [15] |
Moradi B. The new optimization algorithm for the vehicle routing problem with time windows using multi-objective discrete learnable evolution model. Soft Computing, 2020, 24(9): 6741-6769. DOI:10.1007/s00500-019-04312-9 (  0) 0) |
| [16] |
Clarke G, Wright J R. Scheduling of vehicle routing problem from a central depot to a number of delivery points. Operations Research, 1964, 12: 568-581. DOI:10.1287/opre.12.4.568 (  0) 0) |
| [17] |
Solomon M M. Algorithms for the vehicle routing and scheduling problems with time window constraints. Operations Research, 1978, 35: 254-265. (  0) 0) |
| [18] |
Glover F. Future path for integer programming and links to artificial intelligence. Computers and Operations Research, 1986, 13(5): 533-549. DOI:10.1016/0305-0548(86)90048-1 (  0) 0) |
| [19] |
Steinbrunn M, Moerkotte G, Kemper A. Heuristic and randomized optimization for the join ordering problem. The VLDB Journal, 1997, 6(3): 8-17. DOI:10.1007/s007780050040 (  0) 0) |
| [20] |
Yadav P K, Prajapati N L. An overview of genetic algorithm and modeling. International Journal of Scientific and Research Publications, 2012, 2(9): 1-4. (  0) 0) |
| [21] |
Yu X C, Zhang T W. Multiple colony ant algorithm based on particle swarm optimization. Journal of Harbin Institute of Technology, 2010, 42(05): 766-769. (  0) 0) |
| [22] |
Dorigo M, Gambardell L M. Ant colony system: a cooperative learning approach to the traveling salesman problem. IEEE Transactions on Evolutionary Computation, 1997, 41(1): 53-66. DOI:10.1109/4235.585892 (  0) 0) |
| [23] |
Liu L Q, Dai Y T, Wang L H. Ant colony algorithm parameters optimization. Computer Engineering, 2008, 11: 208-210. DOI:10.3969/j.issn.1000-3428.2008.11.075 (  0) 0) |
| [24] |
Chen B W. Application of Ant Colony Optimization in Vehicle Routing Problems. Harbin: Harbin Institute of Technology, 2009.
(  0) 0) |
 2023, Vol. 30
2023, Vol. 30


