An elevator is a frequently used floor vehicle in daily life. The increasing number of elevators has caused frequently-occurring elevator safety accidents due to inadequate supervision and the aging of elevators. Throughout the elevator production, installation, supervision and maintenance, the current accident-prevention models focus on prior supervision but lack effective daily supervision[1]. At the same time, the elevator failure cannot be forewarned due to the lack of corresponding data, which results in frequent failures and causes immense losses to people's lives and property. When the elevator fails, the maintenance personnel cannot arrive at the scene in time and are unable to timely acquire the monitoring data and find the cause of the elevator failure, which makes the elevator rescue very difficult[2]. Real-time data monitoring and artificial intelligence algorithm analysis of elevator operations can immensely benefit the safety of the trapped people. This is of great interest not only to elevator manufacturers, but also government departments, elevator maintenance workers, property management companies and elevator users[3].
The elevator is a kind of special equipment that works intermittently[4] and still retains its normal state. To identify the abnormal working conditions of the elevator or to classify the fault types, it is necessary to specifically analyze the up or down operation process, and locate, segment, and classify the elevator time series. A few specific types of analyses can provide highly accurate estimates of the elevator working conditions. For an intermittent, aperiodic, non-Gaussian time series process[5-7], the traditional anomaly detection technology based on distance and dimension has its limitations, which severely affects the elevator abnormality detection performance. Zheng et al.[8] proposed a fault diagnosis method for excessive elevator vibration. Based on high-order wavelet packet decomposition and neural networks, the features of excessive vibration signals of elevator parts were extracted to identify elevator faults. Zhu et al.[9] proposed a method based on Gabor wavelet transform and multi-core support vector machine to accurately and comprehensively diagnose elevator guide shoe faults. Mishra et al.[10] proposed a deep automatic encoder model for fault classification, which can realize feature extraction of elevator sensor vibration and magnetic signals via the random forest. However, the model had low accuracy due to the low signal to interference noise ratio. To sum up, elevator fault identification mostly depends on the analysis of the vibration signals from the elevator cabin and its parts. The diagnosis performance is poor due to large noise. As the elevator is a kind of lifting and transportation device that depends on motor movement[11-15], changes in traction electromechanical signals can represent changes in elevator state. The safety and reliability of the elevator can be improved by identifying its real-time working conditions through electrical signal analysis. The current signal generated by the elevator traction machine, and the active power signal generated simultaneously with the current, are the main topics of this research because they have excellent performance in identifying the starting and braking of the elevator.
The common fault diagnosis methods for motor current signature analysis (MCSA) include the discrete Fourier transform (DFT)[16] and wavelet transform[17], but these methods are not robust to interference noise. Although the machine learning methods have satisfactory fault diagnosis accuracy, the motor current signal is easily perturbed by the load, especially the maximum starting and braking currents. Furthermore, the different time sequence lengths make it difficult to build fault monitoring model. The reasons for these shortcomings are the difficulty in training and applying recurrent neural network[18]. Lee et al.[19] proposed a one-dimensional convolutional neural network (1DCNN) method to diagnose the inter-turn short circuit fault (ISCF) and demagnetization fault (DF) of an indoor permanent magnet synchronous motor (PMSM). This method was used to successfully locate the motor fault from the three-phase current time series because the current was plagued by background noise.
Time series data generated by different elevator operation processes have different lengths. The difference in sampling interval and elevator load results in the data generated by the same operation process with different sizes. That is to say, the length of the current time series is not equal. Entering the current time series into 1DCNN needs to unify their length, and the common method of unifying the length of the time series is to fill in 0. But this operation destroys the original information of the time series. However, by transforming the time series into images, the advantages of machine vision can be fully utilized. First, the time series is interpolated and then converted into a two-dimensional image to reduce the error interference caused by zero filling. For a time series with unequal length and oscillation, a two-dimensional convolutional neural network (2DCNN) can effectively capture local subtle changes because the convolution kernel processing order and forward direction are different from those of the 1DCNN[20]. In practice, to monitor multiple elevators in real-time, a large sampling interval is usually used. Because the single-variable time series cannot fully explain the co-occurrence and potential state of data[21-23], alternative and richer representations need to be found. When the active power and current are generated synchronously[24-25], the same elevator running process will produce a similar envelope that is suitable for image classification.
In this paper, a new method of elevator condition recognition based on an improved 2DCNN is proposed. First, the current and active power of the elevator traction machine are located and divided in real-time, respectively. Subsequently, they are converted into two-dimensional images and then preprocessed by gray-scaling and binarization. Second, the image recognition is realized based on the 2DCNN and model matching method. Last, the recognition performance under different parameter combinations is analyzed. The parameters of the proposed model are adjusted to effectively improve its performance with respect to the elevator current and power. The parameters are optimized to obtain the training parameters that give the best performance. Aiming at the non-tendentiousness of the low-level active power data, a data description method for hierarchical analysis is proposed to improve the classification accuracy. The experimental results show that the elevator working conditions can be effectively identified and monitored based on the two-dimensional image analysis of elevator traction machine current and active power.
1 Methodology 1.1 Improved 2DCNNThe 1DCNN cannot effectively capture the local abnormal changes because of the convolution kernel processing sequence and forward direction[26]. The 2DCNN is more conducive to the extraction of features from the elevator electrical signal data, due to its better integration of local detail information. This paper proposes an improved 2DCNN based on the Lenet-5 network. Fig. 1 shows the improved 2DCNN structure.
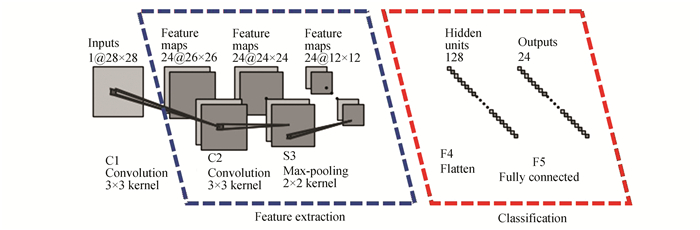
|
Fig.1 Improved 2DCNN structure diagram |
In Fig. 1, C1 is a convolution graph with 24 characteristic graphs, where the size of the convolution kernel filter is 3×3, and the rectified linear units (ReLU) activation function is used. A large number of feature maps are used to extract more primary features from the input image, which can help in obtaining a multi-angle description of the input image. The region of interest becomes smaller because the small convolution kernel size can capture the image details. The convolution method adopted is effective convolution. No zero filling is performed on the input image, and the size of the image obtained at the output of C1 is 26×26.
The mathematical expression of the rectified linear unit[27] is
| $f(x)=\max (0, x) $ | (1) |
where x is the input argument. The output of the ReLU activation function is zero when its independent variable is negative; otherwise, it is the same as the input. This property enables the gradient to be large and consistent as long as the ReLU is active. Moreover, the ReLU renders the output of a few neurons as zero and consequently, the network becomes sparser that reduces the interdependence between different parameters and alleviates the overfitting problem. A few activation functions such as sigmoid have gradient containing regions. The gradient is susceptible to disappear when the gradient descent method is used, leading to information loss. Therefore, using the ReLU can not only alleviate the problem of gradient disappearance but also accelerate the training process.
The convolution layer C2 has 24 characteristic graphs. The size of the convolution kernel is 3×3, and the ReLU activation function is again used. Considering the low complexity of current and effective power gray-scale images, no more feature images are used.
The subsampling layer is denoted by S3, where the size of the pooling area is 2×2, and the pooling method is max-pooling. Its main purpose is dimension reduction. There are four units in the 2×2 region. The size of the feature graph reduces to a quarter of that of the previous layer after pooling. The problem of image recognition is usually concerned with the presence of features in a local region. Therefore, the maximum pooling method is used instead of average pooling because it selects the largest response in the input region. On the other hand, the average pooling method averages the values of the four units in the region, giving an output value that is smaller than that obtained using the maximum pooling method. As the probability of a feature appearing more than twice in a single small area is very small, the maximum pooling will not miss any features.
A full connectivity layer is presented by F4, which contains 128 neurons, and uses the ReLU activation and dropout functions. The latter is a regularization method that forces a neuron to randomly cooperate with other neurons. As a result, the joint adaptability between neurons is weakened and the generalization ability of the network is increased. When the weights in this layer are updated, the hidden layer neurons appear randomly with a certain probability of two neurons not appearing simultaneously. Therefore, the influence of a fixed combination between neurons on network weight updating is reduced. The dropout ratio is set to 0.25.
The last layer F5 is a fully connected layer with 24 neurons, where each neuron corresponds to an elevator condition category. This layer acts as a classifier. The earlier convolution and pooling layers map the original image data from the input space to the feature space of the hidden layer. The layer F5 maps the learned distributed feature representation from the feature space of the hidden layer to the sample label space. Unlike the earlier layers, F5 uses the softmax activation function. This activation function is a generalization of the logistic sigmoid function, where each neuron function output falls in a [0, 1] interval. The output of each neuron is the probability of the sample belonging to a category. The sum of all outputs is 1. The softmax activation function has the following form:
| $ \sigma(z)_j=\frac{e^{z_j}}{\sum\limits_{k=1}^K e^{e^{z_k}}}(j=1, \cdots, K) $ | (2) |
where the total number of categories is K, and σ(z)j is the probability that the sample belongs to class j.
A cross-entropy loss function is used as the loss function instead of a mean square error loss function. It has the following form:
| $ C=-\frac{1}{N} \sum_n[y \ln a+(1-y) \ln (1-a)] $ | (3) |
where C is the loss function value, y is the sample label, a is the expected output value that is the actual network output value, and N is the number of samples. The value of the cross-entropy loss function is non-negative. When a is close to y, C is close to 0. In addition, compared with the mean square error loss function, the cross-entropy loss function leads to faster weight update during the backpropagation process.
The gradient descent method for a small batch size requires the learning rate to be set manually. On the one hand, if the learning rate is too small, the convergence process will be very slow. On the other hand, if the learning rate is too large, the loss function will oscillate or even diverge near the minimum value. This method cannot be adjusted according to the characteristics of a specific data set. Furthermore, it is difficult to avoid the saddle point. During the process of updating the network model parameters, different updating strategies for parameters with different frequencies should be adopted. Therefore, an adaptive learning rate optimization method is considered in this paper.
Adaptive motion estimation (Adam) is a method to calculate the adaptive learning rate of each parameter. In essence, it is the root mean square propagation (RMSprop) with momentum. The parameter update formula for this method is as follows:
| $ \begin{aligned} m_{t+1}= & \beta_1 m_t+\left(1-\beta_1\right) \cdot \nabla_{\theta_t} J_j\left(\theta_t\right) V_{t+1}= \\ & \beta_2 \cdot V_t+\left(1+\beta_2\right)\left(\nabla_{\theta_t} J\left(\theta_t\right)\right)^2 \theta_{t+1}= \\ & \theta_t-\mu \frac{m_{t+1}}{\sqrt{V_{t+1}+\varepsilon}} \end{aligned} $ | (4) |
where the default values of β1 and β2 are 0.9 and 0.999, respectively, and ε=10-8.
The performance of Adam is slightly better than that of RMSprop when the gradient is more sparse at the end of the training, because the former method adds bias correction and momentum. It combines the adaptive gradient algorithm (AdaGrad) that is good at dealing with sparse gradients. The RMSprop is good at dealing with non-stationary objects and has lower memory requirements. It is suitable for most non-convex optimization problems, large data sets, and high-dimensional spaces.
1.2 Descriptive Analysis of Data 1.2.1 SkewnessThe skewness of data samples is calculated according to the Fisher Pearson's skewness coefficient, given as follows:
| $ g_1=\frac{m^3}{m_2^{3 / 2}} $ | (5) |
where
| $G=\frac{k_3}{k_2^{3 / 2}}=\frac{\sqrt{N(N-1)}}{N-2} \cdot \frac{m_3}{m_2^{3 / 2}} $ | (6) |
In probability theory and statistics, the coefficient of variation (CV), also known as the discrete coefficient, is a normalized measure of the discrete degree of a probability distribution. This coefficient can eliminate not only the influence of the differences in data dimensions but also the influence of different mean values. It is defined as the ratio of standard deviation to average, i.e.,
| $ C V=\frac{\sigma}{\mu} $ | (7) |
where σ is the standard deviation and μ is the mean value.
1.2.3 QuantileQuantile is a generalization of the median. When the data are arranged in ascending order, for 0≤q≤1, the q-th quantile is defined as
| $ m_q=\left\{\begin{array}{l} x_{[\mathrm{np}]}+1, \text { if } n \text { is not an integer number } \\ \frac{1}{2}\left(x_{[\mathrm{np}]}+x_{[\mathrm{np}+1]}\right), \text { otherwise } \end{array}\right. $ | (8) |
where [np] denotes the integer part of np. Given a vector X of length N, the q-th quantile of X is the value in ascending order. If the normalized ranking does not match the position of q, the quantile will be determined according to the value and distance of the two nearest neighbors and the interpolation parameters. If q=0.5, the 50th percentile is the median. If q=0, the quantile is the same as the minimum. If q=1.0, the quantile is the same as the maximum.
1.2.4 OscillationAccording to the distribution characteristics of active power data, oscillation can be described as whether the current or active power of the elevator is stable between one-third and two-thirds of the whole elevator operating process. This can be described as follows:
| $ \text { criterion }=\frac{\max +\min }{2} $ | (9) |
where max and min represent the maximum and minimum values in one-third to two-thirds of the time series data, respectively.
Different rules are specified to calculate the number of oscillation points. The oscillation of the active power of the elevator is described by the number of oscillation points. Denoting the time series as {x1 x2 … xN}, the rules are as follows:
| $\operatorname{dot}_{i+1}= \begin{cases}\operatorname{dot}_i+1, x_i \leqslant \text { criteria } \leqslant x_{i+1} \\ \operatorname{dot}_i, \quad \text { otherwise }\end{cases} $ | (10) |
An elevator with six layers that is normally used in a residential area was selected for data monitoring over three days. The experimental data were collected using the data acquisition system based on the elevator Internet of things developed in our laboratory. The collected data included the instantaneous voltage, instantaneous current, active power, floor change, load, and elevator status. The sampling period was 70 ms. During the data collection process, data cleaning was carried out and obvious data errors were eliminated.
The elevator up and down processes are not the same. The different number of floors moved by the elevator and load can affect the current and active power. To take into account this feature, the label XYZHL is specified, where "X" refers to the elevator moving upwards and downwards, i.e., "0" refers to the elevator going down, "1" refers to the elevator going up, "Y" refers to the number of floors that the elevator moves, e.g., "3" refers to the elevator moving three floors, "Z" refers to the elevator load label, with "H" referring to more than 200 kg, and "L" referring to less than 200 kg.
First, a two-dimensional image was generated from the time sequence current data generated in each running process of the elevator. Then, it was converted to gray-scale and binarized. The training and test sets are divided to train the 2DCNN network. The test set accuracy of 97.78% can be achieved. It can be found that the 2DCNN classifies the current two-dimensional image very well, which can provide a feasible means for elevator condition monitoring. The main information of elevator current data is distributed at the starting and braking positions. An appropriate number of convolution kernels can be selected to obtain more detailed information. As shown in Table 1, the different number of convolution kernels in convolution layers C1 and C2 through experiments were studied and the accuracy obtained over the training and test sets is listed. The optimal number of convolution layers in the convolution kernels of C1 and C2 is determined as 24.
| Table 1 Influence of the number of convolution kernels on accuracy |
It can be noted from Fig. 2 that the current images generated by the elevator operating under the same working conditions are similar, which is conducive to the training and recognition of the convolution network. The image processing avoids the location and division of long time series. The number of floors over which the elevator moves affects the length of time series, which is convenient for image classification. In addition, as the shape deviation is mainly affected by the elevator load, the experimental results show that compared with one-dimensional image classification, the two-dimensional image classification method can avoid the impact of load on the elevator current. It can improve the classification accuracy irrespective of the elevator moving down or up.
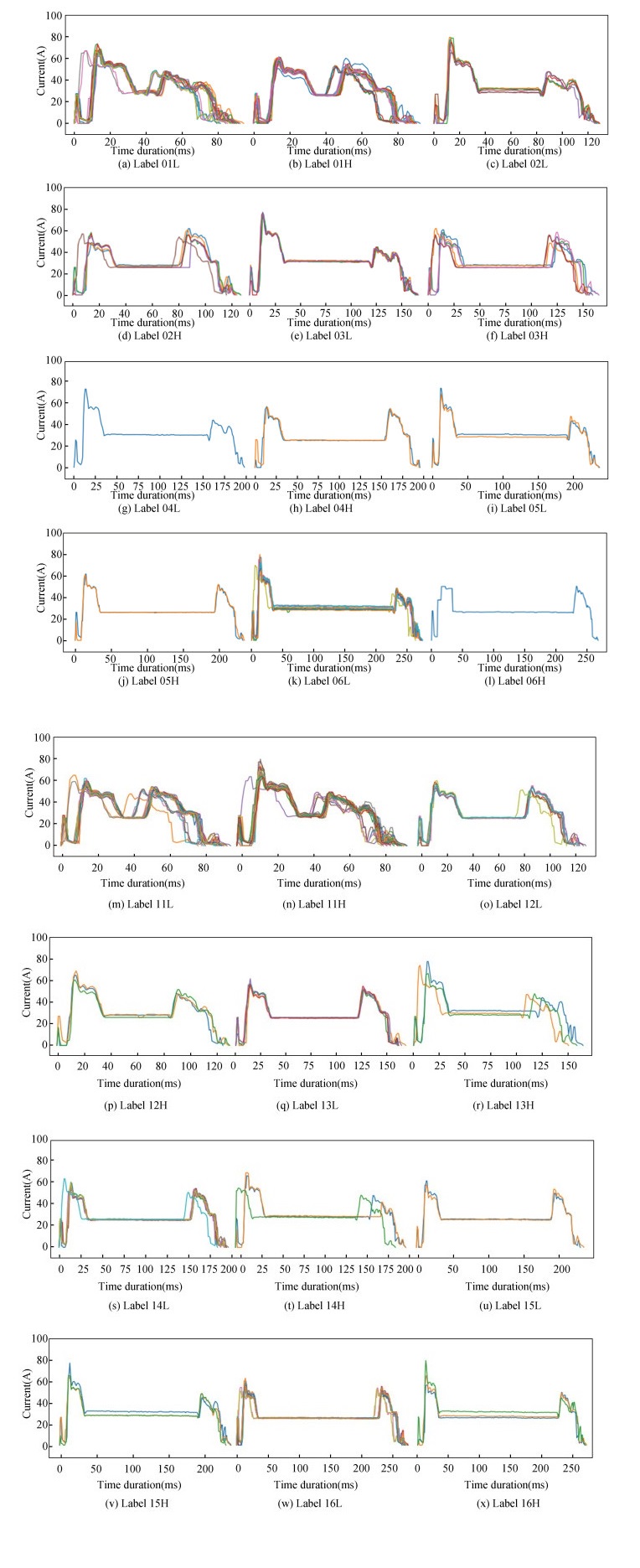
|
Fig.2 Current classification diagram of the elevator going up and down, different floors moved, and different load operation processes |
In the experiments, the same procedure as that used for current is adopted for the active power generated by current synchronization, i.e., generation of the two-dimensional images, followed by gray-scaling and learning through the 2DCNN network. However, the experimental results are not satisfactory. It can be observed from Fig. 3 that the active power of the elevator is not sensitive to weight. A large number of floors were moved by the elevator results in a more obvious trend shown by the effective power. On the contrary, a small number of floors moved by the elevator results in a less obvious trend. The classification accuracy can only be improved by finding the number of floors for downwards motion that is suitable for hierarchical scanning. This number is equal to 1 and 2. Due to the characteristics of the active power envelope, this study proposes to analyze it by skewness, CV, quantile and oscillation.
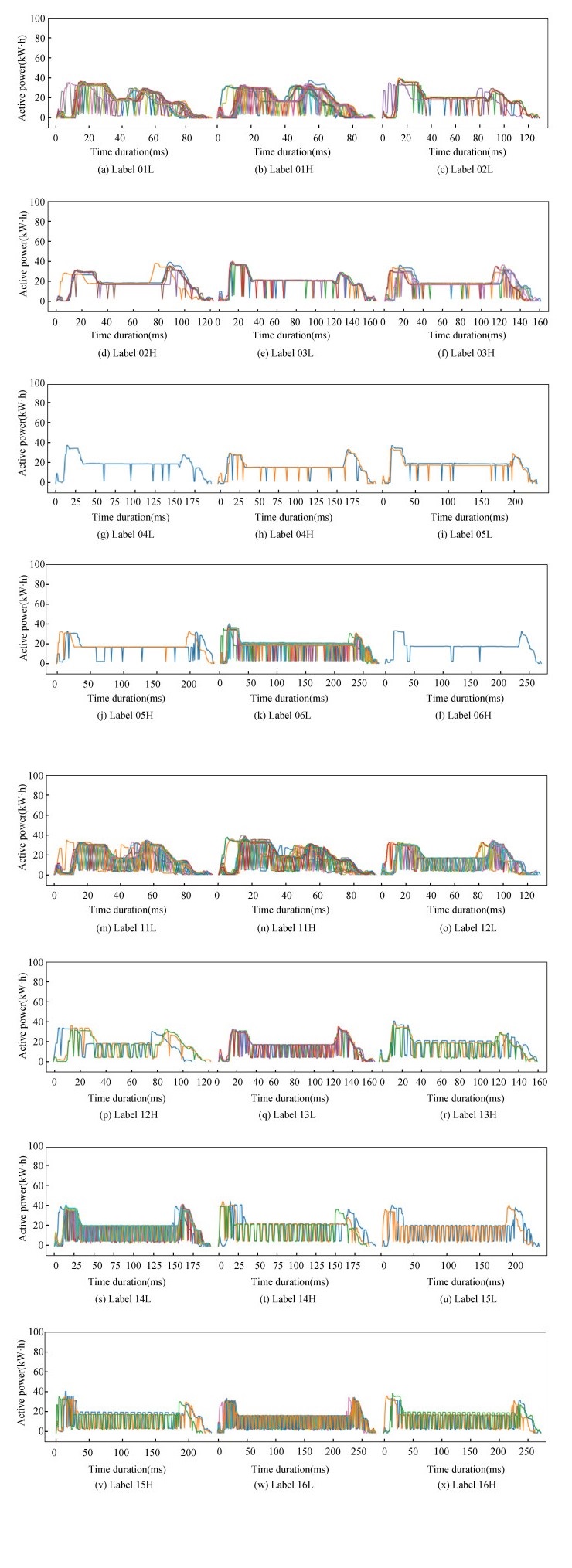
|
Fig.3 Active power classification diagram of the elevator going up and down, different floors moved, and different load operation processes |
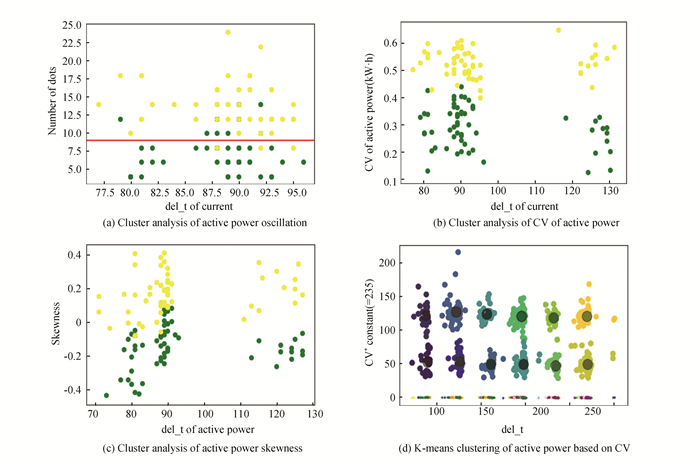
The oscillation, CV, skewness and quantile of the active power were calculated for a total of 871 elevators. As the active power is acquired with a delay, it appears and disappears together with the instantaneous current. Thus, the time sequence length of the instantaneous current was used to describe the data more accurately. Fig. 4 shows the results of classification experiments corresponding to oscillation, CV, skewness and quantile. As shown in Fig. 4(a), the number of oscillation points was set equal to or less than 8 or 14 according to classification error. There are 79 error points in total that give an error rate of 9.07%, which signifies a good classification performance. The active power is not sensitive to load. It can be observed that it is divided into 12 clusters, which correspond to six layers of uplink and six layers of downlink, respectively.
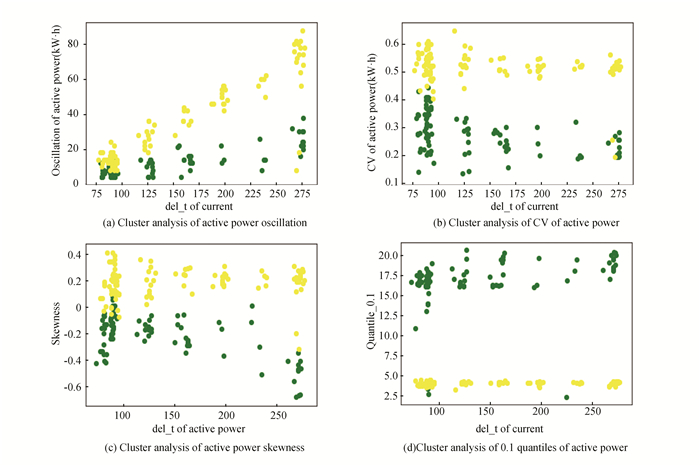
|
Fig.4 Descriptive clustering analysis of active power data |
As can be noted from Fig. 4(a), (b) and (c), the classification performance of the bottom layer, i.e., layers 1 and 2, is not satisfactory. Aiming at the low-level non-tendentiousness of active power, it is not conducive to 2DCNN image recognition. As the active power is not sensitive to weight, a simplified hierarchical analysis is carried out on the bottom data, as well as on the uplink and downlink data of mobile floors 1 and 2. That is, for "01L", "01H", "02L", "02H", "11L", "11H", "12L" and "12H", there are 190 elevator operation processes. As shown in Fig. 5(a), in the descending process, the number of oscillation points greater than 11 is defined as the error points, whereas in the ascending process, the number of oscillation points less than 11 is defined as the error points. A total of 14 error points can be counted, giving an accuracy of 92.64%. As shown in Fig. 5(b), in the descending process, the CV values greater than or equal to 0.4 are defined as the error points, whereas in the ascending process, the CV values less than 0.4 are considered as the error points. A total of 5 error points can be counted, giving an accuracy of 97.37%. As shown in Fig. 5(c), in the descending and ascending processes, the number of oscillation points greater than 0, and the number of oscillation points less than 0 are considered as error points. A total of 13 error points can be counted, giving an accuracy of 93.16%.
|
Fig.5 Descriptive clustering analysis of active power for small movement |
It can be noted from the aforementioned results that compared with other methods, the CV can achieve better active power data classification. 827 new elevator operation processes were collected, their CV was calculated, and a final accuracy of 97.48% was obtained through K-means clustering. This result is close to the identification result of synchronous current data, and can be considered as reliable and useful.
3 ConclusionsThis research was mainly aimed at the identification and monitoring of elevator working conditions. It proposed an innovative use of elevator traction machine current and active power, utilizing new monitoring variables to describe the elevator operation. Consequently, the monitoring of the elevator was no longer limited to the vibration signal analysis of the cabin or other parts. In this study, the use of machine vision technology was introduced to transform the elevator data time series into two-dimensional gray images. Our method achieved an accuracy of 97.78%. The research results have reference and practical values for the identification and monitoring of elevator working conditions. The proposed model can also be used for periodic and discrete mechanical monitoring of other types of equipment. In future work, we will collect different types of fault data, and extend our method to two-dimensional image recognition of different types of faults to improve its effectiveness.
| [1] |
Cai N, Chow W K. Numerical studies on fire hazards of elevator evacuation in supertall buildings. Indoor and Built Environment, 2019, 28(2): 247-263. DOI:10.1177/1420326X17751593 (  0) 0) |
| [2] |
Wen P G, Zhi M, Zhang G Y, et al. Fault prediction of elevator door system based on PSO-BP neural network. Engineering, 2016, 8(11): 761-766. DOI:10.4236/eng.2016.811068 (  0) 0) |
| [3] |
Liu J, Gong Z H, Bai Z L, et al. Analysis of elevator motor fault detection based on chaotic theory. Journal of Information and Computational Science, 2014, 11(1): 229-235. DOI:10.12733/JICS20102695 (  0) 0) |
| [4] |
Wang C, Zhang R J, Zhang Q. Analysis of transverse vibration acceleration for a high-speed elevator with random parameter based on perturbation theory. International Journal of Acoustics and Vibration, 2017, 22(2): 218-223. DOI:10.20855/ijav.2017.22.2467 (  0) 0) |
| [5] |
Syafitri A, Iwa G M K, Ridwan G, et al. Fuzzy-PID simulation on current performance for modern elevator. Proceedings of the 2016 6th IEEE International Conference on Control System, Computing and Engineering (ICCSCE). Piscataway: IEEE, 2016.403-406. DOI: 10.1109/ICCSCE.2016.7893607.
(  0) 0) |
| [6] |
Chen Z P, Wang Z, Zhang G A, et al. Research of big-data-based elevator fault diagnosis and prediction. Mechanical & Electrical Engineering Magazine, 2019, 36(1): 90-94. (in Chinese) DOI:10.3969/j.issn.1001.-4551.2019.01.018 (  0) 0) |
| [7] |
Tao R, Xu Y C, Deng F H, et al. Feature extraction of an elevator guide shoe vibration signal based on SVD optimizing LMD. Journal of Vibration and Shock, 2017, 36(22): 166-171. DOI:10.13465/j.cnki.jvs.2017.22.026 (  0) 0) |
| [8] |
Zheng Q, Zhao C H. Wavelet packet decomposition and neural network based fault diagnosis for elevator excessive vibration. Proceedings of the 2019 Chinese Automation Congress (CAC). Piscataway: IEEE, 2019. 5105-5110. DOI: 10.1109/CAC48633.2019.8996653.
(  0) 0) |
| [9] |
Zhu X L, Li K, Zhang C S, et al. Fault diagnosis method of elevator guide shoe based on Gabor wavelet transform and multi-kernel support vector machine. Computer Science, 2020, 47(12): 258-261. DOI:10.11896/jsjkx.200700039 (  0) 0) |
| [10] |
Mishra K M, Krogerus T R, Huhtala K J. Fault detection of elevator system using profile extraction and deep autoencoder feature extraction for acceleration and magnetic signals. Proceedings of the 2019 23rd International Conference Information Visualisation (IV). Piscataway: IEEE, 2019. 139-144. DOI: 10.1109/IV.2019.00032.
(  0) 0) |
| [11] |
Royo J, Segui R, Pardina A, et al. Machine current signature analysis as a way for fault detection in permanent magnet motors in elevators. Proceedings of the 2008 18th International Conference on Electrical Machines. Piscataway: IEEE, 2008. 10519422. DOI: 10.1109/ICELMACH.2008.4799863.
(  0) 0) |
| [12] |
Zhu M, Wang Z R, Guo W J, et al. Research on the model for elevator failure rate prediction and its application. China Safety Science Journal, 2017, 27(9): 74-78. (in Chinese) DOI:10.16265/j.cnki.issn1003-3033.2017.09.013 (  0) 0) |
| [13] |
Zhu L, Fu Y, Li G M. Research on SVM multi-classification based on particle swarm algorithm. Proceedings of the 2018 International Symposium on Computer, Consumer and Control (IS3C). Piscataway: IEEE, 2018. 18472907. DOI: 10.1109/IS3C.2018.00075.
(  0) 0) |
| [14] |
Zurita D, Sala E, Carino J A, et al. Industrial process monitoring using recurrent neural networks and self-organizing maps. Proceeding of the 2016 IEEE 21st International Conference on Emerging Technologies and Factory Automation (ETFA). Piscataway: IEEE, 2016. 16428980. DOI: 10.1109/ETFA.2016.7733534.
(  0) 0) |
| [15] |
Potluri S, Diedrich C, Sangala G K R. Identifying false data injection attacks in industrial control systems using artificial neural networks. Proceedings of the 2017 22nd IEEE International Conference on Emerging Technologies and Factory Automation (ETFA). Piscataway: IEEE, 2017. 17489114. DOI: 10.1109/ETFA.2017.8247663.
(  0) 0) |
| [16] |
Wang P P, Shi L P, Zhang Y, et al. Broken rotor bar fault detection of induction motors using a joint algorithm of trust region and modified bare-bones particle swarm optimization. Chinese Journal of Mechanical Engineering, 2019, 32(1): 65-78. DOI:10.1186/s10033-019-0325-y (  0) 0) |
| [17] |
Wen X, Wang J Y, Li X. A feed-forward wavelet neural network adaptive observer-based fault detection technique for spacecraft attitude control systems. Chinese Journal of Electronics, 2018, 27(1): 102-108. DOI:10.1049/cje.2017.11.010 (  0) 0) |
| [18] |
Salehinejad H, Sankar S, Barfett J, et al. Recent advances in recurrent neural networks. https://arxiv.org/pdf/1801.01078.pdf.
(  0) 0) |
| [19] |
Lee H, Jeong H, Kim S W. Detection of interturn short-circuit fault and demagnetization fault in IPMSM by 1-D convolutional neural network. Proceedings of the 2019 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC). Piscataway: IEEE, 2019. 19356512. DOI: 10.1109/APPEEC45492.2019.8994556.
(  0) 0) |
| [20] |
Zhao J F, Mao X, Chen L J. Speech emotion recognition using deep 1D & 2D CNN LSTM networks. Biomedical Signal Processing and Control, 2019, 47(1): 211-217. DOI:10.1016/j.bspc.2018.08.035 (  0) 0) |
| [21] |
Liu F G, Zheng J Z, Zheng L L. Combining attention-based bidirectional gated recurrent neural network and two-dimensional convolutional neural network for document-level sentiment classification. Neurocomputing, 2020, 371: 39-50. DOI:10.1016/j.neucom.2019.09.012 (  0) 0) |
| [22] |
Budreski K, Winchell M, Padilla L, et al. A probabilistic approach for estimating the spatial extent of pesticide agricultural use sites and potential co-occurrence with listed species for use in ecological risk assessments. Integrated Environmental Assessment and Management, 2016, 12(2): 315-327. DOI:10.1002/ieam.1677 (  0) 0) |
| [23] |
Xie J, Pang Y W, Hisham C, et al. PSC-Net: learning part spatial co-occurrence for occluded pedestrian detection. Science China (Information Sciences), 2021, 64(2): 120103. DOI:10.1007/s11432-020-2969-8 (  0) 0) |
| [24] |
Fan Y L, Rui X P, Poslad S, et al. A better way to monitor haze through image-based upon the adjusted LeNet-5 CNN model. Signal, Image and Video Processing, 2020, 14: 455-463. DOI:10.1007/s11760-019-01574-6 (  0) 0) |
| [25] |
Zhang C W, Yue X Y, Wang R. Study on traffic sign recognition by optimized Lenet-5 algorithm. International Journal of Pattern Recognition and Artificial Intelligence, 2020, 34(1): 2055003. DOI:10.1142/S0218001420550034 (  0) 0) |
| [26] |
Li T H, Jin D, Du C F, et al. The image-based analysis and classification of urine sediments using a LeNet-5 neural network. Computer Methods in Biomechanics and Biomedical Engineering: Imaging & Visualization, 2020, 8(1): 64-77. DOI:10.1080/21681163.2019.1608307 (  0) 0) |
| [27] |
Bao R X, Yuan X, Chen Z K, et al. Cross-entropy pruning for compressing convolutional neural networks. Neural Computation, 2018, 30(11): 121-143. DOI:10.1162/neco_a_01131 (  0) 0) |
 2023, Vol. 30
2023, Vol. 30


