When the digital circuits are operated near the threshold/moderate inversion region, they are highly sensitive to process variations. Intrinsic and extrinsic factors contribute to process variation. Intrinsic differences are often caused by the limits of the device physics, while extrinsic variations are produced by wafer-to-wafer and die-to-die variations. Although extrinsic differences may be minimized via improved process control, intrinsic variations are uncontrollable and serve as a significant barrier to device scalability. Significant causes of intrinsic variation include the following[1-4]:
1) Random dopant fluctuation: It has been shown in the literature that the quantity and location of dopant atoms implanted are random in nature at a scaled technology node. Due to the extremely small number of dopant atoms in scaled devices, there is a significant fluctuation in the threshold voltage (which is a function of dopant concentration). When the dopant atoms are big, the Poisson distribution may be used to estimate the dopant fluctuations, as opposed to the Gaussian distribution[5-6].
2) Roughness of the line edge: This refers to the variance in the form of the gate along the channel width direction. It happens more often near the mask borders, where bigger material grains dissolve more readily than smaller material grains. The roughness of the line edge does not scale with technology and cannot be decreased via lithographic process control. However, this has an effect on the threshold voltage and leakage current of the device[7-8].
3) Oxide thickness fluctuations: When the oxide layer thickness is a few Si atom layers, the atomic scale roughness at the interface of Si - SiO2 and gate SiO2 produces oxide thickness variations in scaled devices. This has an effect on the carrier mobility and thus on the device's threshold voltage[9-10].
All of the above-mentioned fluctuations become more significant as the technology node scales down, but random dopant fluctuations (which result in threshold variation) become increasingly crucial as the supply voltage drops. It is because the variation in the drain current is asymmetric at the ultradeep submicron channel length and at lower supply voltage. Statistical metrics like mean and standard deviation cannot be used to identify the shape of the distribution[9-10].
Thus, the probability distribution of drain current has been studied using Skewness, a measure of asymmetry. Fig. 1 illustrates the skewness of a CMOS inverter's current distribution with regard to the supply voltage. The findings were acquired using a Monte Carlo simulation with 20000 HSPICE nodes at the 32 nm technology node. As the supply voltage drops, the drain current varies asymmetrically owing to the change in threshold voltage, which is considerably greater than at higher supply voltage.

|
Fig.1 Drain current skewness at various supply voltages for 32 nm technology node |
In general, the variability of any random variable may be expressed as its standard deviation normalized by its mean (σ/μ) value, which indicates its global deviation[11]. This leads to a statistical distribution of performance in comparison with the circuits operating in the strong inversion region. Low voltage operation (in the moderate inversion region) exhibits non-Gaussian delay distribution, enabling utilization of advanced statistical models[12].
Statistical based solutions are classified as either fitting-based or analytical-based. Examples of fitting based non-Gaussian solutions are based on Monte Carlo simulations such as log skew normal distribution, inverse Gaussian distribution, and Weinbull distribution. These distributions have a long simulation time and do not provide any physical insight into the design parameters[13-14]. Many analytical models have been proposed in literature to study the impact of process variations on circuit performance[13-14]. In Ref. [15], log normal distribution for gate delay variation is applied to circuits operating in the subthreshold region. It has been assumed that the threshold voltage follows a Gaussian distribution under process variation. The analysis has been extended to stacked transistors and applied to the NAND gate as an example. In Ref.[16], the gate delay variability (σ/μ) model for subthreshold circuits has been presented analytically with the condition that the correlation between the stacked transistors is derived from generic logic gates under specific corner conditions.
The transregional MOSFET model with closed form equations was developed by Ref. [17]. The model is utilized to generate a log normal delay distribution under variation in threshold voltage by Ref. [18]. Further improvement of the model was given by Ref. [19] that described the micro-architectural statistical timing performance. All the above models followed log normal distribution for delay under threshold voltage variation for low supply voltages. But, none of the models was specific to the moderate inversion region. The following are the major contributions:
1) The unified transregional MOSFET model applicable in the entire range of moderate inversion has been presented to find the delay model for ultradeep submicron technology up to 22 nm.
2) It has been shown that the TRM model[17] verification with BSIM4[20] shows lower errors at the edge of weak inversion, which increases as the transistor moves towards the strong inversion region. But the proposed model is applicable for the entire range of moderate inversions.
3) In order to study variability at the 22 nm technology node, an analytical delay model under threshold voltage (dominant parameter) variation was developed using a log skew normal distribution.
4) The moment matching function has been utilized to calculate an analytical log skew normal based delay model. The distribution parameters are represented as a function of threshold voltage, supply voltage and the number of transistors that are stacked.
5) The proposed model is validated in the entire moderate inversion range using a CMOS inverter as a sample gate.
6) The proposed methodology has been compared with log normal and Monte Carlo simulations done using predictive technology model 22 nm (PTM)[21]. The obtained results were better than that with both the techniques.
7) The proposed model is capable of finding the delay variability, maximum and minimum delay for CMOS inverters at 22 nm.
1 CMOS Inverter Delay DerivationThe velocity versus electric field for electrons in the inversion layer is described as in Ref. [22] where Usat is saturation velocity (m/s), E represents a lateral electric field, while Ec represents the critical field at which the carriers become velocity saturated:
| $ v(E)=\frac{\mu_{\mathrm{eff}} E}{\left[1+\left(\frac{E}{E_{\mathrm{c}}}\right)^M\right]^{\frac{1}{M}}} $ | (1) |
where
| $ E_{\mathrm{c}}=\frac{v_{\text {sat }}}{\mu_{\text {eff }}} $ |
Here, vsat is the saturation velocity, μeff is the effective mobility and M is constant. It is commonly acknowledged in literature that M=2 with electrons and while M=1 for holes. Because the mathematics required to calculate the drain current is difficult and time-consuming, the modified first degree U-E model inserting M=1 with fitting constants a, b, and c is presented below, where
| $ v\left(E_x\right)=\frac{a \mu_z E_x}{\left[b+c\left(\frac{E_x}{E_{\mathrm{c}}}\right)\right]} $ | (2) |
| Table 1 Values of a, b, and c defining the first order U-E relationship extracted for various technology nodes |
and
| $\mu_z=\frac{\mu_0}{1+\theta\left(V_{\mathrm{gs}}-V_{\mathrm{th}}\right)} $ | (3) |
where θ represents coefficient of mobility degradation, Ex is the lateral electric field, μz represents the degradation effect due to vertical field, and μ0 denotes mobility due to low electric field; Vgs is the bias voltage between gate and source; Vth represents the threshold voltage. The relationship between μ and E can be expressed as[23-24]
| $ \mu_{\mathrm{eff}}\left(E_x\right)=\frac{a \mu_z}{\left[b+c\left(\frac{E_x}{E_{\mathrm{c}}}\right)\right]} $ | (4) |
In the presence of parasitic resistance, the mobility degradation coefficient can be expressed as that in Ref. [25]:
| $ \theta_m=\theta+\beta_0 R_{\mathrm{s}} $ | (5) |
where β0 denotes the maximum value of device transconductance, θ represents coefficient of mobility degradation, and Rs represents the value of device series resistance.
PTM[21, 26] describes the effect of velocity overshoot as
| $ V_{\mathrm{sat}}=V_{\mathrm{sato}}+0.13 \mu_{\mathrm{eff}} \sqrt{\tau \mu_{\mathrm{eff}} \frac{k T}{q}}\left(\frac{V_{\mathrm{ds}}}{L^2}\right) $ | (6) |
where Vsato represents the carrier velocity saturation without overshoot; τ denotes the transition time of the charge carriers to travel from source to drain; Vds represents the applied bias potential from drain to source; L is the effective channel length, k is the Boltzmann constant, T is the temperature and q is the unit charge.
Normalizing every quantity to make it unitless[27]:
| $ q_{\mathrm{i}}=\frac{-Q_{\mathrm{i}}}{2 n \phi_{\mathrm{t}} C_{\mathrm{ox}}} $ | (7) |
where qi indicates the normalized value of the inversion charge Qi, n is the slope factor, Cox is the oxide capacitance and ϕt is the thermal voltage.
| $ I_0=2 n \mu \frac{W}{L} \phi_{\mathrm{t}}^2 C_{\text {ox }} $ | (8) |
where I0 indicates technological current, W is the channel width and μ is the carrier mobility.
| $ v_{\mathrm{c}}=\frac{V_{\mathrm{c}}}{\phi_{\mathrm{t}}} $ | (9) |
where vc indicates the normalized value of channel potential, Vc.
| $ i(\text { drain current })=\frac{I}{I_0} $ | (10) |
where i indicates the normalized value of drain current I.
| $ u=\frac{\mu_{\text {eff }}\left(E_{x}\right)}{\mu_{z}} $ | (11) |
where u indicates mobility.
| $ e=\frac{\left|E_{x}\right|}{E_{\mathrm{c}}}=-\lambda_{\mathrm{c}} \frac{\mathrm{d} q_{\mathrm{i}}}{\mathrm{d} \xi} $ | (12) |
where e represents horizontal electric field, λc is the coefficient velocity saturation and is a function of effective channel length and ξ is the normalized position along x-axis.
| $ i_{\mathrm{ds}}=-\left(2 q_{\mathrm{i}}+1\right) u \frac{\mathrm{d} q_{\mathrm{i}}}{\mathrm{d} \xi} $ | (13) |
Putting u from Eq. (11) in Eq. (13) and rearranging,
| $i_{\mathrm{ds}} b \mathrm{~d} \xi=-\left(a\left(2 q_{\mathrm{i}}+1\right)-c \lambda_{\mathrm{c}} i_{\mathrm{ds}}\right) \mathrm{d} q_{\mathrm{i}} $ | (14) |
where ids is the device drain to source current.
Integrating Eq. (14) from ξ=0 and qi=qs to ξ=1 and qi=qd,
| $ i_{\mathrm{ds}}=\frac{a\left(q_{\mathrm{s}}^{2}-q_{\mathrm{d}}^{2}+q_{\mathrm{s}}-q_{\mathrm{d}}\right)}{b+c \lambda_{\mathrm{c}}\left(q_{\mathrm{s}}-q_{\mathrm{d}}\right)} $ | (15) |
where qs indicates normalized inversion charge at the source end, and qd indicates inversion charge at the drain end.
In order to further simplify Eq. (15), assume a=b=c=1
| $ i_{\mathrm{ds}}=\frac{q_{\mathrm{s}}^{2}-q_{\mathrm{d}}^{2}+q_{\mathrm{s}}-q_{\mathrm{d}}}{1+\lambda_{\mathrm{c}}\left(q_{\mathrm{s}}-q_{\mathrm{d}}\right)} $ | (16) |
The inversion charge density in the presence of velocity saturation, i.e., when qi=qdsat[27],
| $ i_{\mathrm{dsat}}=\frac{2 q_{\mathrm{dsat}}}{\lambda_{\mathrm{c}}} $ | (17) |
| $v_{\text {dsat }}=v_{\mathrm{p}}-2 q_{\text {dsat }} $ | (18) |
| $ \begin{gathered} q_{\mathrm{d}}= \begin{cases} \frac{v_{\mathrm{p}}-v_{\mathrm{d}}}{2}, & \text { if } v_{\mathrm{d}} <v_{\mathrm{dsat}} \\ q_{\mathrm{dsat}}, & \text { if } v_{\mathrm{d}} \geqslant v_{\mathrm{dsat}}\end{cases} \end{gathered} $ | (19) |
where qdsat, vdsat, vp, vd, are the normalized values of saturated drain charge, saturated drain voltage, pinch-off voltage and drain voltage.
For qdsat, utilizing Eq.(16) and Eq.(17) at ids=idsat,
| $ \frac{2 q_{\mathrm{dsat}}}{\lambda_{\mathrm{c}}} =\frac{q_{\mathrm{s}}^{2}-q_{\mathrm{dsat}}^{2}+q_{\mathrm{s}}-q_{\mathrm{dsat}}}{1+\lambda_{\mathrm{c}}\left(q_{\mathrm{s}}-q_{\mathrm{dsat}}\right)} $ | (20) |
| $ \begin{aligned} q_{\mathrm{dsat}} & =\frac{1}{2 \lambda_{\mathrm{c}}}\left[\lambda_{\mathrm{c}}\left(1+2 q_{\mathrm{s}}\right)-\right. \\ & \left.\sqrt{\lambda_{\mathrm{c}}^{2}+4 \lambda_{\mathrm{c}}\left(1+2 q_{\mathrm{s}}\right)+4}+2\right] \end{aligned} $ | (21) |
| $ \begin{aligned} i_{\mathrm{dsat}}= & \frac{2}{\lambda_{\mathrm{c}}^{2}}\left[1+\frac{1}{2} \lambda_{\mathrm{c}}\left(1+2 q_{\mathrm{s}}\right)-\right. \\ & \left.\frac{1}{2} \sqrt{\lambda_{\mathrm{c}}^{2}+4 \lambda_{\mathrm{c}}\left(1+2 q_{\mathrm{s}}\right)+4}\right] \end{aligned} $ | (22) |
The relationship of inversion charge density and channel potential can be expressed following the Ref. [17] and expressed in Eq. (23) where ka, k2 and k3 denotes fitting coefficients; vy=vp-vc, vp represents normalized value of pinch off potential, vc denotes the voltage across the channel and vy is the voltage across channel y-axis,
| $ q_i \approx k_a \mathrm{e}^{k_2 v_y+k_3 v_y^2} $ | (23) |
where Vp is the unnormalized pinch-off voltage, Vg is the unnormalized gate voltage, Vth is the unnormalized threshold voltage, and ka is the fitting coefficient.
Unnormalize Eq. (22), and substitute qi from Eq. (23). Consider source reference and deep saturation, considering
| $A=k_a \mathrm{e}^{k_2 \frac{\mathrm{VG}}{n \phi_{\mathrm{t}}}+k_3\left(\frac{\mathrm{VG}}{n \phi_{\mathrm{t}}}\right)^2}, \mathrm{VG}=V_{\mathrm{gs}}-V_{\mathrm{th}} $ | (24) |
| $\begin{aligned} & I_{\mathrm{dsat}}=2 n \mu_z \frac{W}{L} \phi_t^2 C_{\mathrm{ox}}\left[\frac{1}{4}\left(\frac{E_{\mathrm{c}} L}{\phi_{\mathrm{t}}}\right)^2 .\right. \\ & \left.\left(\sqrt{\left(\frac{\phi_{\mathrm{t}}}{E_{\mathrm{c}} L}\right)^2+\frac{2 \phi_{\mathrm{t}}}{E_{\mathrm{c}} L}(1+2 A)+1}-1\right)^2-\frac{1}{4}\right] \end{aligned} $ | (25) |
where VG is the overdrive voltage, Vgs is the gate to source voltage, A is the multiplying factor and Idsat is the drain saturation current.
Eq. (25) corresponds to drain current for short channel devices considering both the valid drift and diffusion component in all three operating regions. For the moderate inversion region, when the field is low, expand the expression in Eq. (25) through binomial expansion and take initial terms:
| $ \begin{gathered} I_{\mathrm{dsat}}=n \mu \frac{W}{L} \phi_{\mathrm{t}}^{2} C_{\mathrm{ox}} \frac{1}{2}\left[\left(\frac{\phi_{\mathrm{t}}}{4 E_{\mathrm{c}} L}\right)^{2}+(1+2 A)^{2}+\right. \\ \left.\left(\frac{\phi_{\mathrm{t}}}{2 E_{\mathrm{c}} L}\right)(1+2 A)-1\right] \end{gathered} $ | (26) |
| $ I_{\mathrm{dsat}}=2 n \mu \frac{W}{L} \phi_{\mathrm{t}}^{2} C_{\mathrm{ox}}\left[A^{2}+A\right] $ | (27) |
Substituting A from Eq. (24),
| $ \begin{gathered} I_{\mathrm{dsat}}=2 n \mu \frac{W}{L} \phi_{\mathrm{t}}^{2} C_{\mathrm{ox}}\left[\left(k_{a} e^{k_{2} \frac{\mathrm{VG}}{n \phi_{\mathrm{t}}}+k_{3}\left(\frac{\mathrm{VG}}{n \phi_{\mathrm{t}}}\right)^{2}}\right)^{2}+\right. \\ \left.k_{a} \mathrm{e}^{k_{2} \frac{\mathrm{VG}}{n \phi_{\mathrm{t}}}+k_{3}\left(\frac{\mathrm{VG}}{n \phi_{\mathrm{t}}}\right)^{2}}\right] \end{gathered} $ | (28) |
At low supply voltage, the first exponent term is neglected:
ION is the current that is described as drain current when Vgs=Vds=supply voltage Vdd. Therefore, in above equation, defining technology current IS=2nμ ϕt2Cox.
| $ I_{\mathrm{ON}}=I_{S} \frac{W}{L} K_{a} e^{Z} $ | (29) |
| $ Z=\mathrm{e}^{k_{2} \frac{\mathrm{VG}}{\phi_{\mathrm{t}}}}+k_{3}\left(\frac{\mathrm{VG}}{n \phi_{\mathrm{t}}}\right)^{2} $ | (30) |
where Z is the constant factor.
The RC delay of CMOS inverter can be expressed as td as described in Eq. (31) where Kd is the fitting parameter, and CL denotes the load capacitance. The average value of Kd shall be utilized to reduce the fitting error:
| $ t_{\mathrm{d}}=K_{\mathrm{d}} \frac{V_{\mathrm{dd}} C_{L}}{I_{\mathrm{ON}}} $ | (31) |
The logarithmic expression of Eq. (31) can be written as
| $ Y=\ln \left(t_{\mathrm{d}}\right)=-Z+C_{t_{\mathrm{d}}} $ | (32) |
The delay of the gate is assumed to follow a log skew normal distribution. Therefore, its logarithmic form expressed in Eq. (32) follows a skew normal distribution whose probability density function can be written as[28]
| $f_{\mathrm{SN}}(Y)=\frac{2}{\omega} \phi\left(\frac{Y-\epsilon}{\omega}\right) \varPhi\left(\lambda \frac{Y-\epsilon}{\omega}\right) $ | (33) |
Here,
| $ \epsilon=\mu-\omega \beta \sqrt{\frac{2}{\pi}} $ | (34) |
| $ \omega=\sqrt{\frac{\sigma^{2}}{1-\frac{2}{\pi} \beta^{2}}} $ | (35) |
| $ \beta=\frac{\pi}{2} \frac{\left(\frac{2 \gamma_{1}}{4-\pi}\right)^{\frac{2}{3}}}{1+\left(\frac{2 \gamma_{1}}{4-\pi}\right)^{\frac{2}{3}}} $ | (36) |
where
| $ \lambda=\frac{\beta}{\sqrt{1-\beta^{2}}} $ | (37) |
From Eq. (30) and Eq. (32), it can be seen that Y is dependent on threshold voltage. Y can be calculated from the mean (first moment), variance (second moment) and standard deviation (third moment) assuming a Gaussian distribution of threshold voltage. The following are the expressions:
| $ \mu=-\frac{k_{2}}{n \phi_{\mathrm{t}}} E\left[V_{\mathrm{d} t}\right]-\frac{k_{3}}{\left(n \phi_{\mathrm{t}}\right)^{2}} E\left[V_{\mathrm{d} t}^{2}\right]+C_{t_{\mathrm{d}}} $ | (38) |
| $\sigma^{2}=\frac{k_{3}^{2}}{\left(n \phi_{\mathrm{t}}\right)^{4}}\left(E\left[V_{\mathrm{d} t^{\prime}}^{4}\right]-E\left[V_{\mathrm{d} t^{\prime}}^{2}\right]^{2}\right) $ | (39) |
| $ \begin{gathered} \gamma_{1}=\frac{-\frac{k_{3}^{3}}{\left(n \phi_{\mathrm{t}}\right)^{6}}\left(E\left[V_{\mathrm{d} t^{\prime}}^{6}\right]+\frac{3}{4} \frac{k_{2}^{2} k_{3}}{\left(n \phi_{\mathrm{t}}\right)^{4}} E\left[V_{\mathrm{d} t^{\prime}}^{4}\right]\right)}{\sigma^{3}}+ \\ \frac{\frac{3}{16} \frac{k_{2}^{4}}{\left(n \phi_{\mathrm{t}}\right)^{2} k_{3}} E\left[V_{\mathrm{d} t^{\prime}}^{2}\right]}{\sigma^{3}}+\frac{\frac{k_{2}^{6}}{64 k_{3}^{3}}-3 \mu \sigma^{2}-\mu^{3}}{\sigma^{3}} \end{gathered} $ | (40) |
Vdt and Vdt' are the expressions that follow Gaussian distribution and expressed in Eq. (41) and Eq. (42),
| $ V_{\mathrm{d} t}=V_{\mathrm{dd}}-V_{\mathrm{th}} \sim N\left(V_{\mathrm{dd}}-\mu_{0}, \sigma_{0}\right) $ | (41) |
| $ \begin{aligned} V_{\mathrm{d} t^{\prime}}=V_{\mathrm{dd}}-V_{\mathrm{th}}+\frac{n \phi_{\mathrm{t}} k_{2}}{2 k_{3}} \sim N\left(V_{\mathrm{dd}}-\mu_{0}+\right. \\ \left.\quad \frac{n \phi_{\mathrm{t}} k_{2}}{2 k_{2}}, \sigma_{0}\right) \end{aligned} $ | (42) |
where Vdt and Vdt′ are the expressions that follow Gaussian distribution. Further, in Eq. (38), Eq. (39) and Eq. (40), several terms can be described as
| $ E\left[V_{\mathrm{d} t^{\prime}}^{2}\right]=\sigma_{0}^{2}+\left(E\left[V_{\mathrm{d} t^{\prime}}\right]\right)^{2} $ | (43) |
| $ E\left[V_{\mathrm{d} t^{\prime}}^{4}\right]=3 \sigma_{0}^{4}+6 \sigma_{0}^{2}\left(E\left[V_{\mathrm{d} t^{\prime \prime}}\right]\right)^{2}+ \\ \left(E\left[V_{\mathrm{d} t^{\prime \prime}}\right]\right)^{4} $ | (44) |
| $ E\left[V_{\mathrm{d} t^{\prime}}^{6}\right]=15 \sigma_{0}^{6}+45 \sigma_{0}^{4}\left(E\left[V_{\mathrm{d} t^{\prime}}\right]\right)^{2}+ \\ 15 \sigma_{0}^{2}\left(E\left[V_{\mathrm{d} t^{\prime \prime}}\right]\right)^{4}+\left(E\left[V_{\mathrm{d} t^{\prime \prime}}\right]\right)^{6} $ | (45) |
where
| $ E\left[V_{\mathrm{d} t}\right]=V_{\mathrm{dd}}-\mu_{0} $ | (46) |
| $ E\left[V_{\mathrm{d} t^{\prime}}\right]=V_{\mathrm{dd}}-\mu_{0}+\frac{n \phi_{\mathrm{t}} k_{2}}{2 k_{3}} $ | (47) |
| $ E\left[V_{\mathrm{d} t^{\prime \prime}}\right]=V_{\mathrm{dd}}-\mu_{0}+\frac{\frac{k_{2}}{n \phi_{\mathrm{t}}}}{\frac{k_{3}}{\left(n \phi_{\mathrm{t}}\right)^{2}}} $ | (48) |
Eqs.(38)-(40) show that most of the parameters can be obtained from fitting, whether they are process dependent or process independent, except the mean and standard deviation of the device threshold voltage. The mean value of the Gaussian-distributed threshold voltage can be utilized as the nominal value for various device sizes in SPICE simulations. Monte Carlo simulations are performed to find the standard deviation for the smallest transistor at each process node. For long channel transistors, Pelgrom's Law which states that the standard deviation is inversely to find the standard deviation[29]. The amount of effort required for Monte Carlo simulations is reduced to one at different values of the transistor size and the load capacitance because of the model explained in Eqs.(38)-(40). By combining Eqs.(34)-(36) with Eqs.(38)-(40), the distribution parameters
Now, Td follows log skew normal distribution with distribution parameters the same as skew normal distributed Y[30]. Thus,
| $ T_{\mathrm{d}} \sim \operatorname{LSN}\left(\epsilon, \omega^{2}, \lambda\right) $ | (49) |
Its PDF and CDF can be expressed as
| $ f_{\mathrm{LSN}}\left(t_{\mathrm{d}}\right) =\frac{2}{\omega y} \phi\left(\frac{\ln \left(t_{\mathrm{d}}\right)-\epsilon}{\omega}\right) \varPhi\left(\lambda \frac{\ln \left(t_{\mathrm{d}}\right)-\epsilon}{\omega}\right) $ | (50) |
| $\begin{aligned} F_{\mathrm{LSN}}\left(t_{\mathrm{d}}\right) =\varPhi\left(\frac{\ln \left(t_{\mathrm{d}}\right)-\epsilon}{\omega}\right)-2 T\left(\lambda \frac{\ln \left(t_{\mathrm{d}}\right)-\epsilon}{\omega}, \lambda\right) \end{aligned} $ | (51) |
Here, Owen's function T can be expressed as
| $ T\left(\frac{\ln \left(t_{\mathrm{d}}\right)-\epsilon}{\omega}, \lambda\right)=\frac{1}{2 \pi} \int_{0}^{\lambda} \cdot \frac{\mathrm{e}^{\frac{-\ln \left(t_{\mathrm{d}}\right)-\epsilon^{2}}{\omega}}\left(1+t^{2}\right)}{1+t^{2}} \mathrm{~d} t $ | (52) |
where t indicates real variable (the frequency parameter).
The mean and variance of the gate delay can be expressed as (after finding PDF and CDF)
| $ E_{t_{\mathrm{d}}}=2 \mathrm{e}^{\epsilon} \mathrm{e}^{\frac{\omega^{2}}{2}} \phi(\beta \omega) $ | (53) |
| $ D_{t_{\mathrm{d}}}=2 \mathrm{e}^{2 \epsilon} \mathrm{e}^{\omega^{2}}\left(\mathrm{e}^{\omega^{2}} \phi(2 \beta \omega)-2 \phi^{2}(\beta \omega)\right) $ | (54) |
For the log skew normal distributed model for delay, the points of ±3σ percentile can be obtained by setting the CDF given in Eq. (51) to be equal to Φ(±3) represented as
| $ \begin{array}{r} F_{\mathrm{LSN}}(Y)=\varPhi\left(\frac{\ln (Y)-Y}{\omega_{Y}}\right)-2 T\left(\frac{\ln (Y)-\epsilon_{Y}}{\omega_{Y}}, \lambda_{Y}\right)= \\ \varPhi( \pm 3) \end{array} $ | (55) |
where λY denotes the shape parameter.
Now, in order to solve the above equation, the shape distribution parameter of delay td in log skew normal distribution is approximately taken to a value close to 1. Using the Owen's function,
| $ T(h, 1)=\frac{1}{2} \varPhi(h)(1-\varPhi(h)) $ | (56) |
where h is a numeric vector.
The above equation can be derived from
| $ \varPhi^{2}\left(\frac{\ln (Y)-\epsilon_{Y}}{\omega_{Y}}\right)=\varPhi( \pm 3) $ | (57) |
The maximum and minimum 3σ or -3σ percentile points are located at
| $ t_{\mathrm{dmax}}=\mathrm{e}^{\epsilon_{Y^{+}} \varPhi^{-1}(\sqrt{\varPhi(3)}) \omega_{Y}} \approx \mathrm{e}^{\epsilon_{Y}+3.21 \omega_{Y}} $ | (58) |
| $ t_{\mathrm{d} \min }=\mathrm{e}^{\epsilon_{Y^{+}} \varPhi^{-1}(\sqrt{\varPhi(3)}) \omega_{Y}} \approx \mathrm{e}^{\epsilon_{Y}-1.79 \omega_{Y}} $ | (59) |
Putting the values of
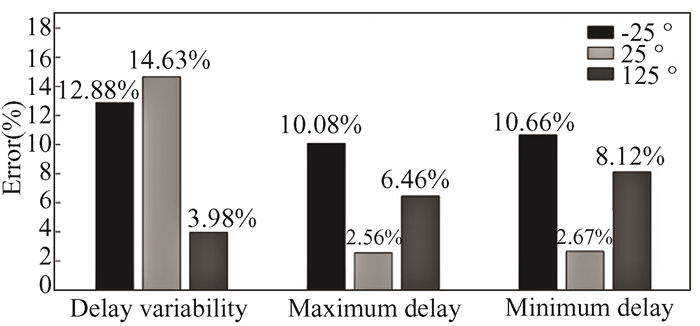
First of all, the drain current of the proposed model is verified and compared with the industry standard BSIM4 and TRM models[17] for the entire range of the moderate inversion as shown in Fig. 2. It can be seen from the figure that the TRM model deviates at the end of moderate inversion or when the transistor moves towards the strong inversion region (The percentage error increases up to 20%). For the 22 nm technology node, the values of ka, k1 and k2 are 0.532, 0.701 and 0.0037 respectively. The probability density function of the proposed model is compared with the results obtained from Fig. 3 which shows the PDF of the CMOS inverter gate with FO4 load. It can be seen from the figure that the proposed model has good agreement with Monte Carlo simulations. In order to evaluate the accuracy of the proposed model, the delay variability, maximum and minimum values of delay have been considered as the performance metrics. The delay variability is calculated by normalizing the standard deviation of the gate delay by its mean value. The maximum and minimum points are generally calculated to approximate the performance in extreme conditions. Figs. 4-6 show the delay variability, maximum and minimum values of the CMOS inverter with FO4 load at three different temperatures.

|
Fig.2 Comparison of the proposed model (refer to Eq. (25)), weak inversion approximation[27] and strong inversion model of Ref. [31] with TRM approximation of drain current[17] |

|
Fig.3 PDF of CMOS inverter with FO4 load (Vdd= 0.25 V) |

|
Fig.4 Delay variability, maximum and minimum values of CMOS inverter with FO4 load (Vdd=0.25 V) |

|
Fig.5 Delay variability, maximum and minimum values of CMOS inverter with FO4 load (Vdd=0.35 V) |
|
Fig.6 Delay variability, maximum and minimum values of CMOS inverter with FO4 load (Vdd=0.45 V) |
4 Conclusions
In this paper, an accurate mathematical log skew normal distributed gate delay model is presented for transistors operating specifically in the moderate inversion region. For worst-case analysis, the cumulative distribution function is used in conjunction with the position scale and shape parameter to determine the maximum and minimum value of delay. The proposed model has excellent agreement with Monte Carlo simulation and is better than the existing statistical delay models when compared variability in delay.
| [1] |
Mittal S. A survey of architectural techniques for nearthreshold computing. ACM Journal on Emerging Technologies in Computing Systems (JETC), 2015, 12(4): 1-26. DOI:10.1145/2821510 (  0) 0) |
| [2] |
Kou L B. Impact of Process Variations on Soft Error Sensitivity of 32-nm VLSI Circuits in Near-Threshold Region. https://ir.vanderbilt.edu/bitstream/handle/1803/12068/LingboKouMasterThesis2014Spring.pdf?sequence=1&isAllowed=y.
(  0) 0) |
| [3] |
Singh K, de Gyvez J P. Twenty years of near/sub-threshold design trends and enablement. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2021, 68(1): 5-11. DOI:10.1109/TCSⅡ.2020.3040970 (  0) 0) |
| [4] |
Gebregiorgis A, Golanbari M S, Kiamehr S, et al. Maximizing energy efficiency in NTC by variation-aware microprocessor pipeline optimization. Proceedings of the 2016 International Symposium on Low Power Electronics and Design. New York: ACM, 2016. 272-277. DOI: 10.1145/2934583.2934635.
(  0) 0) |
| [5] |
Dash T P, Jena J, Mohapatra E, et al. Role of stress/strain mapping and random dopant fluctuation in advanced CMOS process technology nodes. International Journal of Nano and Biomaterials, 2020, 9(1-2): 18-33. (  0) 0) |
| [6] |
Zhang K, Lu W F, Si P, et al. Suppression of timing variations due to random dopant fluctuation by back-gate bias in a nanometer CMOS inverter. Recent Advances in Electrical and Electronic Engineering, 2021, 14(3): 339-346. DOI:10.2174/2352096513666201208102615 (  0) 0) |
| [7] |
Jha C K, Gupta C, Gupta A, et al. Impact of LER on mismatch in nanosheet transistors for 5 nm - CMOS. Proceedings of the 2020 4th IEEE Electron Devices Technology and Manufacturing Conference (EDTM). Piscataway: IEEE, 2020. 1-4.
(  0) 0) |
| [8] |
Shin C. Line Edge Roughness (LER). https://link.springer.com/chapter/10.1007/978-94-017-7597-7_2.
(  0) 0) |
| [9] |
Yang F L, Hwang J R, Li Y M. Electrical characteristic fluctuations in sub-45nm CMOS devices. Proceedings of the IEEE Custom Integrated Circuits Conference 2006. Piscataway: IEEE, 2006. 691-694. DOI: 10.1109/CICC.2006.320881.
(  0) 0) |
| [10] |
Kuhn K. Managing Process Variation in Intel's 45 nm CMOS Technology. https://www.semanticscholar.org/paper/Managing-Process-Variation-in-Intel%E2%80%99s-45nm-CMOS-Kuhn/2b98177c69346835a8b347bedf1789b8934d53bc.
(  0) 0) |
| [11] |
Jamaa H B, Boroujeni B K, de Micheli G, et al. Design technologies for nanoelectronic systems beyond ultimately scaled CMOS. Micheli G, Leblebici Y, Gijs M, et al. Nanosystems Design and Technology. Boston: Springer, 2009. 45-84.
(  0) 0) |
| [12] |
Zjajo A, Tang Q, Berkelaar M, et al. Stochastic analysis of deep-submicrometer CMOS process for reliable circuits designs. IEEE Transactions on Circuits and Systems I: Regular Papers, 2011, 58(1): 164-175. DOI:10.1109/TCSI.2010.205529158 (  0) 0) |
| [13] |
Slimani M, Silveira F, Matherat P. Variability modeling in near-threshold CMOS digital circuits. Microelectronics Journal, 2015, 46(12): 1313-1324. DOI:10.1016/j.mejo.2015.10.001 (  0) 0) |
| [14] |
Kim K, Han S, Park Y M, et al. Validating Log-normal Distribution of Delay Variability in Near-Threshold Design. https://dtl.yonsei.ac.kr/docs/International_Conference/[2016][ITC-CSCC]Validating%20Log-normal%20Distribution%20of%20Delay%20Variability%20in%20Near-Threshold%20Design_deleted.pdf.
(  0) 0) |
| [15] |
Kim S, Agrawal V D. Analytical Delay and Variations Modeling in the Subthreshold Region. https://www.eng.auburn.edu/~agrawvd/TALKS/NCUR16/NCUR.pdf.
(  0) 0) |
| [16] |
Zhang Y Q, Calhoun B H. Fast, accurate variation-aware path timing computation for sub-threshold circuits. Proceedings of the Fifteenth International Symposium on Quality Electronic Design. Piscataway: IEEE, 2014.243-248. DOI: 10.1109/ISQED.2014.6783332.
(  0) 0) |
| [17] |
Keller S, Harris D M, Martin A J. A compact transregional model for digital CMOS circuits operating near threshold. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2014, 22(10): 2041-2053. DOI:10.1109/TVLSI.2013.2282316 (  0) 0) |
| [18] |
Jun S, Ishihara T, Onodera H. Microarchitectural-level statistical timing models for nearthreshold circuit design. Proceedings of the 20th Asia and South Pacific Design Automation Conference. Piscataway: IEEE, 2015. 87-93. DOI: 10.1109/ASPDAC.2015.7058986.
(  0) 0) |
| [19] |
Drego N, Chandrakasan A, Boning D. Lack of spatial correlation in MOSFET threshold voltage variation and implications for voltage scaling. IEEE Transactions on Semiconductor Manufacturing, 2009, 22(2): 245-255. DOI:10.1109/TSM.2009.2017645 (  0) 0) |
| [20] |
Dunga M V, Xi X M, He J, et al. Bsim4. 6.0 Mosfet Model. Berkeley: The Regents of the University of California, 2006. 30-37.
(  0) 0) |
| [21] |
Nanoscale Integration and Modeling (NIMO) Group. Introduction to Predictive Technology Model. http://ptm.asu.edu/.
(  0) 0) |
| [22] |
Arora N. Mosfet Modeling for VLSI Simulation: Theory and Practice. New Jersey: World Scientific, 2007: 276-284.
(  0) 0) |
| [23] |
Enz C, Chicco F, Pezzotta A. Nanoscale MOSFET modeling: Part 1: The simplified EKV model for the design of low-power analog circuits. IEEE Solid-State Circuits Magazine, 2017, 9(3): 26-35. DOI:10.1109/MSSC.2017.2712318 (  0) 0) |
| [24] |
Enz C, Chicco F, Pezzotta A. Nanoscale MOSFET modeling: Part 2: Using the Inversion Coefficient as the Primary Design Parameter. IEEE Solid-State Circuits Magazine, 2017, 9(4): 73-81. DOI:10.1109/MSSC.2017.2745838 (  0) 0) |
| [25] |
Arora N. MOSFET Modeling for VLSI Simulation. New Jersey: World Scientific, 2007: 102-103.
(  0) 0) |
| [26] |
Zhao W, Cao Y. New generation of predictive technology model for sub-45 nm early design exploration. IEEE Transactions on Electron Devices, 2006, 53(11): 2816-2823. DOI:10.1109/TED.2006.884077 (  0) 0) |
| [27] |
Enz C C, Vittoz E A. Charge-Based MOS Transistor Modeling: the EKV Model for Low-Power and RF IC Design. Chichester: Wiley, 2006. (  0) 0) |
| [28] |
Li X, Wu Z J, Chakravarthy V D, et al. A low-complexity approximation to lognormal sum distributions via transformed log skew normal distribution. IEEE Transactions on Vehicular Technology, 2011, 60(8): 4040-4045. DOI:10.1109/TVT.2011.2163652 (  0) 0) |
| [29] |
Pelgrom M J M, Duinmaijer A C J, Welbers A P G. Matching properties of MOS transistors. IEEE Journal of Solidstate Circuits, 1989, 24(5): 1433-1439. DOI:10.1109/JSSC.1989.572629 (  0) 0) |
| [30] |
Harris D M, Keller B, Karl J, et al. A transregional model for near-threshold circuits with application to minimum-energy operation. Proceedings of the 2010 International Conference on Microelectronics. Piscataway: IEEE, 2010. 64-67.
(  0) 0) |
| [31] |
Im H, Song M, Hiramoto T, et al. Physical Insight into Fractional Power Dependence of Saturation Current on Gate Voltage in Advanced Short Channel MOSFETs (Alpha-Power Lawmodel). https://dl.acm.org/doi/epdf/10.1145/566408.566414.
(  0) 0) |
 2023, Vol. 30
2023, Vol. 30


