2. Computer Engineering Techniques Department, Al-Kitab University, Kirkuk 36001, Iraq;
3. Department of Petroleum Technology, Koya Technical Institute, Erbil Polytechnic University, Erbil 44001, Iraq
Researchers have been concentrating on the use of nanofluids to improve convective heat transfer performance recently. Heat exchangers are used to transmit heat while preventing the mixing of fluids with different surface temperatures[1-2]. Heat exchangers (heat pipes, shell tubes, dual pipes, etc.) and vehicular ventilation systems are two examples of the many applications for thermofluidic systems (radiator in a vehicle).
Large volumes of heat can be transferred efficiently, affordably, and effectively with shell and tube heat exchangers. Shell and tube heat exchangers exist in several sizes and designs, and they can accept a wide range of flow rates while minimizing pressure loss, as opposed to other types of exchangers like flat plate and pressured heat exchangers. Metallic and non-metallic particles that disperse in a liquid, such as glycerol, ethylene glycol, water, or oil, and have a diameter of 1 to 100 nanometers are defined nanofluids[3-5]. The characteristics of nanocomposites have been studied by several authors in recent years, and it is believed that the next generation of heat transfer technology will be the best because of these studies.
The features of nanocomposites have been studied by several authors in recent years, and it is believed that the next generation of heat transfer technology will be the best because of its higher thermal efficiency than traditional heat transfer fluids[6-9]. One of the factors contributing to the widespread use of nanoscale materials is that they have different thermophysical and mechanical properties from basic materials[10-12].
Numerous numerical studies have been conducted on improving the performance of the shell-and-tube heat exchanger by using nanofluids. One of these studies was done by the researcher Hussein et al.[13] conducted a numerical study using the simulation program to improve the heat transfer in the shell and tube exchanger by using Al2O3/water nanofluids as a cooling medium instead of distilled water and by volume ratios (0.3%, 0.5%, 0.75%, 1%, 2%). Where this research study was conducted to study the effect of Pecklet number and the type of particles and volumetric ratios on heat transfer. The results showed that adding nanoparticles to distilled water leads to an improvement in heat transfer properties. The results also showed that the Nusselt number increases as the nanoparticles concentration and Peclet number increase. The results also showed that the pressure drop increases more than when using distilled water. Saberi et al.[14] used single-phase and batter models to compare the effects of three nanofluids exposed to forced thermal transfer in a horizontal tube under constant wall temperature circumstances. According to the findings, the two-stage mixture model matched better, and as particle concentration rises, so does the heat transmission coefficient, and heat transmission is increased by increasing the Peclets number.
Kalteh et al.[15] performed a computational study of forced convection to transfer heat of copper-aqueous nanofluid inside a thermally heated nanotube under a laminar flow condition. By using a bimodal Eulerian fluid, the heat transmission property of the nanofluid was simulated. According to the results, as the Reynolds number and particle concentration increase, the heat transfer efficiency increases. Heat transmission on the other hand upsurges as the diameter of the nanoparticle's reduction and the decrease in pressure of nanofluids was also marginally greater than that of basic liquids. Banka et al.[16] conducted a theoretical study on the laminar flow system, through the thermal transfer of nanofluid flow via a straight round when the boundary conditions are constant of the heat flow. The findings showed that the concentration of nanoparticles and Brownian motion are significant sources for improving heat transmission performance, while the diameter of the nanoparticles has an adverse effect on the thermal transfer efficiency.
Raja et al.[17] studied thermal analysis in a shell and tube heat exchanger by using Titanium Carbide, Titanium Nitride, and Zink-Oxide Nanofluids. When compared to other fluids in CFD simulation, Titanium Nitride nanofluids with copper tubes produce a greater heat flux. Experimental approaches were used to analyze the convective transport coefficient for nanoparticles of aluminum oxide and transformer oil flowing through a dual pipe heat exchanger in a laminar flow state (Chun et al.[18]). The results revealed that as the concentration of nanofluid upsurges, the convection coefficient upsurges. Furthermore, Nanoparticle surface properties, particle loading, and particle shape all play a role in improving nanofluid heat transport properties. Esfahani[19] investigated the impact of various factors on the thermal efficiency of grapheme oxide nanofluids in a shell and tube heat exchanger using exergy analysis. The findings revealed that graphene oxide nanofluids improve heat transmission in both laminar and turbulent flow regimes. Azeez et al.[20] investigated the heat transfer properties of Al2O3/water nanofluids in a shell and tube, as well as in a twin pipe heat exchanger by using experimental and CFD analysis. At a volume concentration of 0.5 %, they discovered a substantial increase in heat transfer coefficient of up to 23.9%.
Sajjad et al.[21] conducted numerical calculations using Al2O3/water nanofluids to optimize the heat exchange of the shell and tube heat exchanger at 1%, 2%, 3%, 4% as volume ratios. The results showed that there is a good agreement between the numerical data for water and the results obtained from the Gnielinski correlation with a maximum deviation of about 3%. The calculation also showed that at Re = 7500 and 4% concentration, there was an increase in Nusselt number and convective heat transfer coefficient by 9.5% and 13.5%, respectively.
Previous works treated the improvement of performance of the shell-and-tube heat exchanger by using various nanofluids, but little has been done by researchers in the field of using nanofluids in improving the heat transfer properties. In this research work, the effectiveness of this material and how to improve the performance of the shell and tube heat exchanger will be demonstrated. In the present work, consideration was given to the effect of nanofluids on the rate of heat transfer, the coefficient of friction and the Nusselt number in the condition of laminar flow, the Reynolds number and nanoparticle concentration ranged from 200-1400, 0.2% and 0.35%, respectively. Constant entry temperature, entry velocity, and exit pressure are part of the simulation's boundary conditions. For the heat exchanger applications in this analysis, potential convection stimulated heat transfer while increasing the thermal properties and thermal energy efficiency of the nanofluid.
1 Nanofluid's Physical PropertiesPhysical properties of distilled water and ZnO nanofluid (viscosity (μnf), density (ρnf), thermal conductivity (knf), specific heat (Cp nf) are shown in Table 1. To extract the theoretical values for the properties of the nanofluids, the forms below are used[22].
| $ \mu_{\mathrm{nf}}=\mu_{\mathrm{bf}}(1+2.5 \emptyset) $ | (1) |
| $ \rho_{\mathrm{nf}}=(1-\emptyset) \rho_{\mathrm{f}}+\emptyset \rho_{\mathrm{p}} $ | (2) |
| $ k_{\mathrm{nf}}=\frac{k_{\mathrm{p}}+2 k_{\mathrm{w}}+2\left(k_{\mathrm{p}}-k_{\mathrm{w}}\right) \emptyset}{k_{\mathrm{p}}+2 k_{\mathrm{w}}-\left(k_{\mathrm{p}}-k_{\mathrm{w}}\right) \emptyset} k_{\mathrm{w}} $ | (3) |
| $ C_{P_{\mathrm{nf}}}=\frac{(1-\emptyset)\left(\rho c_{\mathrm{p}}\right)_{\mathrm{f}}+\emptyset\left(\rho c_{\mathrm{p}}\right)_{\mathrm{p}}}{(1-\emptyset) \rho_{\mathrm{f}}+\emptyset \times \rho_{\mathrm{p}}} $ | (4) |
| Table 1 Characteristics of water and nanomaterial at temperature of 293.15 K |
where kp and kw are the thermal conductivity of solid and water respectively; ρ is the density; Cp, the specific heat capacity; ρf, the density of the base fluid; ρp, the nanomaterial density.
Based on the density of the base fluid (ρf) and nanomaterial density (ρp) at 293.15 K, Eq. (5) was used to calculate the concentration, ϕ, of the nanofluid[23].
| $ \phi=\left(\frac{m_{\mathrm{p}}}{\left(m_{\mathrm{p}}+m_{\mathrm{f}}\right)}\right) \times 100 $ | (5) |
where mp is the mass of solid nanoparticles; mf is the mass of base fluid.
In this study, ZnO nanoparticles of (20-30) nm are used and mixed at a concentration of (0.2%, 0.35%) with pure water as a basic liquid. Table 1 demonstrates the characteristics of pure water and nanoparticles.
1.1 CFD AnalysisComputational fluid dynamics (CFD) is a technique for predicting fluid movement, heat and mass transfer, chemical reactions, and a variety of other engineering problems involving fluid flow. The specific problem is expressed in the form of a mathematical model that controls the physical equation. This is accomplished using numerical techniques. In this paper, we seek to optimize the heat exchanger of shell and tube performance by reaching the optimum design by means of computer modeling[24]. Computational fluid dynamics (CFD) technique, which contains different numerical methods and several computer algorithms, has been used to solve and analyze problems that concern fluid flow.
This technique allows the researcher to know the enthalpy distribution, the entropy distribution, kinetic energy, turbulence intensity, density, and other parameters, but in our study, we will be satisfied with the distribution of pressure, temperature, and velocity. The calculations required to simulate fluid-flow with surfaces defined by boundary conditions, and the initial conditions were done by ANSYS/FLUENT 2020R1 Solver. The Navier-Stokes equations form the primary basis for solving fluid dynamics problems. The Continuity equation, Energy equation and the Navier-Stokes equation govern the fluid flow within the exchanger[25].
1.2 Numerical ProcedureThe numerical procedures of the program are divided into four main parts, namely: First, drawing the geometric shape of the laboratory space that is shown in Fig. 1 with real dimensions and determining the direction of flow. Secondly, the distribution of the network of points on all parts of the space is decreed, as the optimal distribution of points must be chosen, and at this stage, the optimal network is tested (Grid Independent Test). Third, controlling and choosing the governing equations, as the program contains equations covering most types of heat transfer and flow, determining the type of fluid used and the mineral, establishing the studied space's boundary conditions (wall, velocity inlet, axis, pressure outlet) and choosing the solution method. Fourth, the final step is to check the results of this solution, with the experimental data or the correlation equations.
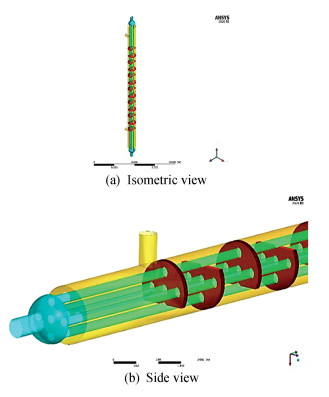
|
Fig.1 Heat exchanger geometry |
The results should be close to the theoretical or experimental values. The grid independence test of the network was conducted, which increased the size of the divisions in the arithmetic field, and then repeated the loop until convergence.
In the simulation of the search model, the model was divided into seven values represented by the number of elements according to the following (2000000, 4000000, 6000000) and dependent on the Reynolds number with the range between Re=200 and Re=650. Fig. 2 shows the grid of the heat exchanger test bench at the tetrahedral element. In the test, a maximum Nusselt number of 6000000 has been recorded and the test results show that all elements are proper for employing in this study. Last values obtained as shown in Fig. 3. The dimensions and details of the physical geometry are summarized in Table 2.
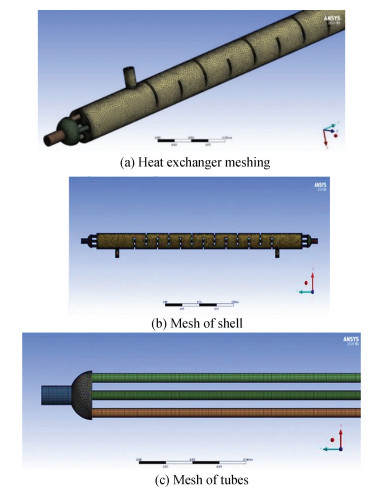
|
Fig.2 Grid of heat exchanger test bench at tetrahedral element |

|
Fig.3 Grid independent test |
| Table 2 Geometric dimensions of the heat exchanger |
1.3 Data Collection
In this work, ZnO nanoparticles are dispersed in pure water to examine the efficiency of nanofluids as well as the coefficient of thermal convection and Nusselt number. Therefore, the equations below can be used in the calculation. The base fluid's and nanofluid's heat transport rates can be computed using the formula below:
| $ Q=\dot{m} \cdot C_{\mathrm{p}} \Delta T $ | (6) |
where Q is rate of heat transfer, W; m is mass flowrate, kg/s; T is temperature, K.
The Nusselt number (Nu) equation and thermal convection coefficient of the base fluid and nanofluids can be determined using the expression below:
| $ N_{\mathrm{u}}=h D / k $ | (7) |
| $ h=\frac{Q}{A\left(T_{\mathrm{w}}-T_{\mathrm{b}}\right)} $ | (8) |
| $ T_{\mathrm{f}}=\frac{T_{\text {in }}+T_{\text {out }}}{2} $ | (9) |
where Nu represents the Nusselt number; h is convective heat transfer coefficient, W/m2·K; D is diameter, m; k is thermal conductivity, W/m·K; A is area of heat transfer, m2; Tw is wall temperature, K; Tf is fluid temperature, K; Tin is inlet temperature, K; Tout is outlet temperature, K; Tb is the bulk temperature (℃).
To compute the nanofluids' total heat transmission coefficient within the tube, the following formula is used[25].
| $ \frac{1}{U_{\mathrm{i}}}=\frac{1}{h_{\mathrm{i}}}+\frac{D_{\mathrm{i}} \operatorname{Ln} \frac{D_{\mathrm{o}}}{D_{\mathrm{i}}}}{2 k_{\mathrm{W}}}+\frac{D_{\mathrm{i}}}{D_{\mathrm{o}}}+\frac{1}{h_{\mathrm{o}}} $ | (10) |
where Ui represente the inlet velocity; hi and ho represente the heat transfer coefficient at the inner and outer tubes; kw is the thermal conductivity of water; Di and Do are represented the inner and outer diameter.
According to the nanofluids and base fluid used, the percentage of efficiency is calculated using the following equation for laminar flow[26].
| $ \eta=\left(\frac{N u_{\mathrm{nf}}}{N u_{\mathrm{f}}}\right) /\left(\frac{f_{\mathrm{nf}}}{f_{\mathrm{f}}}\right)^{\frac{1}{3}} $ | (11) |
where η is the effeciency; Nunf and Nuf are the Nusselt number of nanofluid and basefluid respectively; fnf and ff are the friction factor of nanofluid and basefluid respectively.
To calculate the Nusselt number theoretically using different correlation, we used the definition of Shah London[27], Sieder-Tate[28], and the new correlation developed in Ref. [29], respectively, and compared with CFD results:
| $ \begin{array}{l} N_{\mathrm{u}}=4.364+0.0722\left(\operatorname{Re}_{D_{\mathrm{h}}} \operatorname{Pr} \frac{D_{\mathrm{h}}}{L}\right) \\ \;\;\;\text { for }\left(\operatorname{Re} \cdot \operatorname{Pr} \cdot D_{\mathrm{h}} / L\right)<33.33 \end{array} $ | (12a) |
| $ \begin{aligned} N_{\mathrm{u}}= & 1.953\left(\operatorname{Re}_{D_{\mathrm{h}}} \operatorname{Pr} \frac{D_{\mathrm{h}}}{L}\right)^{\frac{1}{3}} \text { for }(\operatorname{Re} \cdot \operatorname{Pr} \cdot \\ & \left.D_{\mathrm{h}} / L\right) \geqslant 33.33 \end{aligned} $ | (12b) |
| $ N_{\mathrm{u}}=0.4381 \operatorname{Re}^{0.36} \operatorname{Pr}^{0.42} $ | (13) |
| $ N_{\mathrm{u}}=3.66+\frac{0.065 \operatorname{Re} \cdot \operatorname{Pr} \frac{D}{L}}{1+0.04\left(\operatorname{Re} P T \frac{D}{L}\right)^{2 / 3}} $ | (14) |
where Re represents Reynold number; ReDh is the hydraulic diameter; Pr is Prandtl number; Dh is Hydraulic diameter, m; L is length, m; P is density, kg/m3.
2 Results and DiscussionThe heat transfer augmentation, when using nanofluids, was investigated in a counter flow of shell and tube heat exchanger using nanopowder ZnO with a base fluid of deionized the water with two volume fractions of (0.2% and 0.35%) and four Reynolds numbers of (200, 600, 1000, 1400). The convergence of governing equations is conducted to allow recording all results.
2.1 Validation of Current DataTo validate the results of the current study, corrected equations from Nusselt number are used to find out the extent of the matching between the extracted results and the corrected equations. The numerical results were compared with those obtained from the theoretical equation, Eq. (14). As shown in Fig. 4, it was found that there is a good agreement between the current study and those of the theoretical equations used.
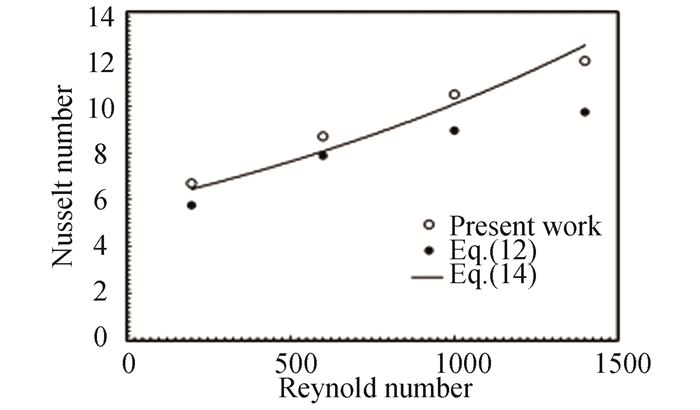
|
Fig.4 Validation with base fluid |
Fig. 5 depicts a standard example of water and nanofluid temperature distribution with (Re =200) 0.2%, 0.35% vol, respectively. The temperature distribution through the heat exchanger is depicted on the color diagram. It can be seen that the color of the temperature contour is changing from blue at the bottom to red at the top. This means the liquid temperature is increasing from the bottom to the top of heat exchanger. The increasing of temperature is approximately 13% due to loss of large quantities of liquid temperature[26].
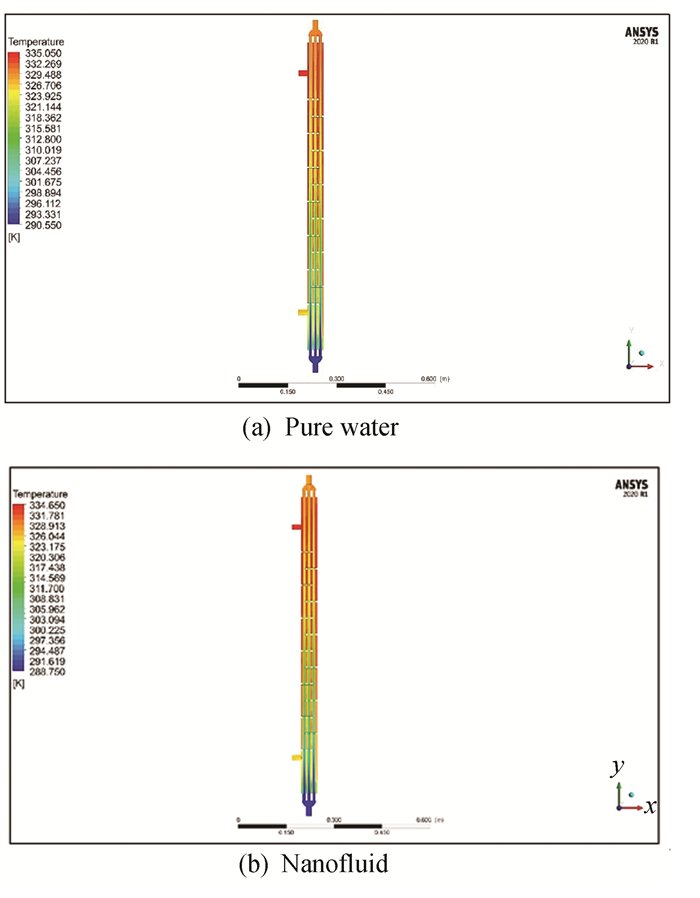
|
Fig.5 Contours of temperatures distribution |
As shown in Fig. 6, it indicates the velocity flow line along the heat exchanger, and the velocity is gradually distributed from entry to and during entry into the pipes.
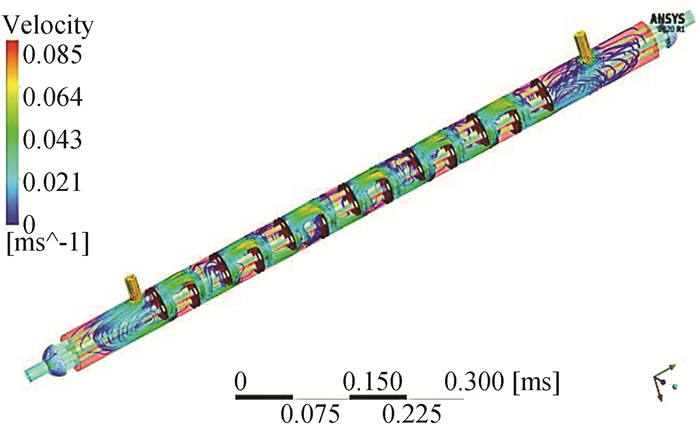
|
Fig.6 Streamline of velocity |
2.2 Nusselt Number
Fig. 7 shows the variation in Nusselt number with different Reynolds number for tube side in the case of counter flow, and with different volume fractions of nanofluids (ZnO/water), (0.2%, 0.35%). Based on the results obtained, it can be noticed that the Nusselt number increases as the particle concentration and the Reynolds number increase. The maximum enhancement of the nanofluids Nusselt number was determined to be about 10% and 19% at 0.2% and 0.35%, respectively. The reason for these increases is due to the different thermal characteristics of the nanofluids from the distilled water. The findings of this research are similar in terms of the principle of the increase in Nusselt number with the researchers of Ref. [26-30].
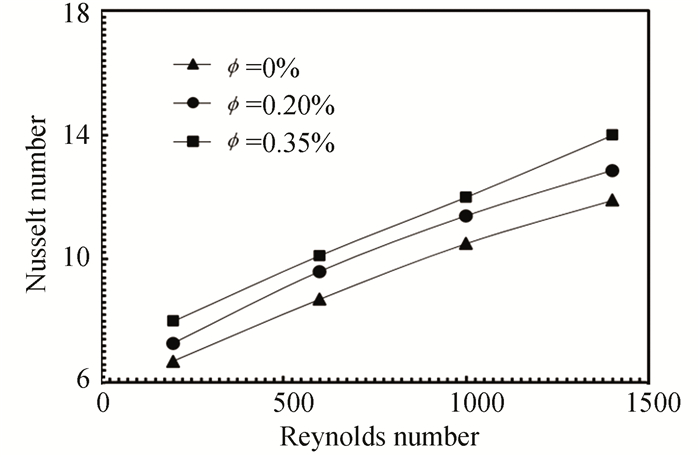
|
Fig.7 Various Reynolds numbers with Nusselt number |
2.3 Friction Factor
Fig. 8 shows the variation in the friction factor value with different Reynolds number at the volume fractions (0.2%, 0.35%) for the nanofluid. It was observed that the coefficient of friction decreases with increasing Reynolds number, while it increases with increasing concentration of nanoparticles in the base-fluid, and this is consistent with most researchers. The decrease in the coefficient of friction was attributed to the increase in the density and viscosity of the nanofluid when nanoparticles were added to the base fluid (pure water). The increase in the friction coefficient at the volumetric ratios of 0.2% and 0.35% was 0.25% and 0.47%, respectively. The study*s friction factor results agreed with those in Refs. [28-30].
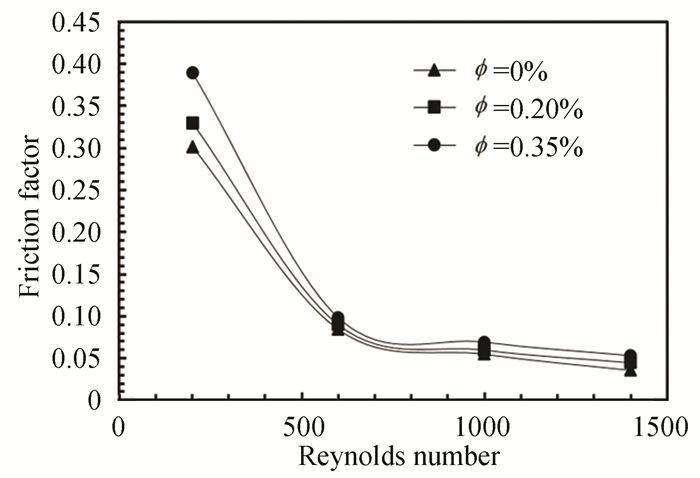
|
Fig.8 Friction factor at different Reynolds numbers |
3 Conclusions
Convective heat transfers and flow properties through nanofluid in STHE have been investigated numerically. ZnO nanoparticles of about 30 nm diameter were used under conditions of laminar-flow in counter-flow heat exchanger of shell and tube. The following conclusions were made based on the findings.
1) When a nanofluid was used, a higher Nusselt number and total heat transmission coefficient were observed, with the reinforcement of the Reynolds number. It was also found that at certain Reynolds numbers, the two factors above increased when using nanofluid at a higher concentration.
2) Adding ZnO nanoparticles to the base liquid augmented its thermal conductivity. The heat transmission can be influenced by friction between fluid and nanoparticles, Brownian Nano particulate movement, and decreasing border layer thickness.
3) As for the coefficient of friction, it was observed that there was a slight increase when using the nanofluid.
4) It was noticed through the results that a high improvement was obtained in the performance of heat transfer when using the nanofluid, and the maximum improvement factor was at a concentration of 0.35%, reaching approximately 12%.
5) The recommended future work is to use different nanofluid by changing type, concentration and diameter.
| [1] |
Azeez K, Hameed A F, Hussein A M. Nanofluid heat transfer augmentation in a double pipe heat exchanger. AIP Conference Proceeding, 2020, 2213(1): 020059. DOI:10.1063/5.0000243 (  0) 0) |
| [2] |
Rasheed A H, Hussein A M. Improving the performance of split air conditioner by adding nano silver to the compressor oil. Journal of Petroleum Research and Studies, 2021, 11(4): 76-90. DOI:10.52716/JPRS.v11i4.564 (  0) 0) |
| [3] |
Hussein Adnan M, Sharma K V, Bakar R A, et al. A review of forced convection heat transfer enhancement and hydrodynamic characteristics of a nanofluid. Renewable and Sustainable Energy Reviews, 2014, 29: 734-743. DOI:10.1016/j.rser.2013.08.014 (  0) 0) |
| [4] |
Gupta S K, Verma H, Yadav N. A review on recent development of nanofluid utilization in shell & tube heat exchanger for saving of energy. Materials Today: Proceedings, 2022, 54: 579-589. DOI:10.1016/j.matpr.2021.09.455 (  0) 0) |
| [5] |
Hussein A M. Adaptive Neuro-Fuzzy Inference System of friction factor and heat transfer nanofluid turbulent flow in a heated tube. Case Studies in Thermal Engineering, 2016, 8: 94-104. DOI:10.1016/j.csite.2016.06.001 (  0) 0) |
| [6] |
Said Z, Rahman S, Ei Haj Assad M, et al. Heat transfer enhancement and life cycle analysis of a Shell-and-Tube Heat Exchanger using stable CuO/water nanofluid. Sustainable Energy Technologies and Assessments, 2019, 31: 306-317. DOI:10.1016/j.seta.2018.12.020 (  0) 0) |
| [7] |
Hussein A M. Thermal performance and thermal properties of hybrid nanofluid laminar flow in a double pipe heat exchanger. Experimental Thermal and Fluid Science, 2017, 88: 37-45. DOI:10.1016/j.expthermflusci.2017.05.015 (  0) 0) |
| [8] |
Ramirez-Tijerina R, Rivera-Solorio C I, Singh J, et al. Numerical study of heat transfer enhancement for laminar nanofluids flow. Applied Sciences, 2018, 8(12): 2661. DOI:10.3390/app8122661 (  0) 0) |
| [9] |
Hazbehian M, Mohammedi M, Maddah H, et al. Analyses of exergy efficiency for forced convection heat transfer in a tube with CNT nanofluid under laminar flow conditions. Heat and Mass Transf, 2017, 53(5): 1503-1516. DOI:10.1007/s00231-016-1915-1 (  0) 0) |
| [10] |
Abdulmajeed B A, Majeed N S. Study and analysis of concentric shell and double tube heat exchanger using γ-Al2O3 nanofluid. Journal of Engineering, 2017, 23(9): 50-62. DOI:10.31026/j.eng.2017.09.04 (  0) 0) |
| [11] |
Mintsa H A, Roy G, Nguyen C T, et al. New temperature dependent thermal conductivity data for water-based nanofluids. International Journal of Thermal Sciences, 2009, 48(2): 363-371. DOI:10.1016/j.ijthermalsci.2008.03.009 (  0) 0) |
| [12] |
Akhgar A, Toghraie D, Sina N, et al. Developing dissimilar artificial neural networks (ANNs) to prediction the thermal conductivity of MWCNT-TiO2/water-ethylene glycol hybrid nanofluid. Powder Technology, 2019, 355: 602-610. DOI:10.1016/j.powtec.2019.07.086 (  0) 0) |
| [13] |
Hussein Adnan M, Sharma K V, Bakar R A, et al. The effect of nanofluid volume concentration on heat transfer and friction factor inside a horizontal tube. Journal of Nanometerials, 2013, 2013: Article No. 1. DOI: 10.1155/2013/859563.
(  0) 0) |
| [14] |
Saberi M, Kalbasi M, Alipourzade A. Numerical study of forced convective heat transfer of nanofluids inside a vertical tube. Journal of Nanometer, 2013, 3(1): 10-15. (  0) 0) |
| [15] |
Kalteh M, Abbassi A, Saffar-Avval M, et al. Eulerian-Eulerian two-phase numerical simulation of nanofluid laminar forced convection in a microchannel. International Journal of Heat and Fluid Flow, 2011, 32(1): 107-116. DOI:10.1016/j.ijheatfluidflow.2011.08.001 (  0) 0) |
| [16] |
Banka H, Raju P, Srinivasulu P. Thermal analysis of shell and tube heat exchanger using titanium carbide, titanium nitride and zink oxide nanofluids. International Research Journal of Engineering and Technology, 2016, 3(8): 1045-1050. (  0) 0) |
| [17] |
Raja M, Vijayan R, Vivekananthan R, et al. Numerical investigation on heat transfer of Al2O3/water nanofluid in a shell and tube heat exchanger. Applied Mechanics and Materials, 2014, 591: 3-6. DOI:10.4028/www.scientific.net/AMM.591.3 (  0) 0) |
| [18] |
Chun B H, Kang U H, Kim S H. Effect of alumina nanoparticles in the fluid on heat transfer in double-pipe heat exchanger system. Korean Journal of Chemical Engineering, 2008, 25(5): 966-971. DOI:10.1007/s11814-008-0156-5 (  0) 0) |
| [19] |
Esfahani M R, Languri E M. Exergy analysis of a shell-and-tube heat exchanger using graphene oxide nanofluids. Experimental Thermal and Fluid Science, 2017, 83: 100-106. DOI:10.1016/j.expthermflusci.2016.12.004 (  0) 0) |
| [20] |
Azeez K, Ibrahim Z, Hussein A. Thermal conductivity and viscosity measurement of ZnO nanoparticles dispersing in various base fluids. Journal of Advance Research in Fluid Mechanics and Thermal Sciences, 2020, 66(2): 1-10. (  0) 0) |
| [21] |
Sajjad M, Ali H, Sajid M. Thermal-hydraulic analysis of water based ZrO2 nanofluids in segmental baffled shell and tube heat exchangers. Thermal Science, 2020, 24(2): 1195-1205. DOI:10.2298/TSCI180615291S (  0) 0) |
| [22] |
Vanaki S M, Ganesan P, Mohammed H A. Numerical study of convective heat transfer of nanofluids: A review. Renewable and Sustainable Energy Reviews, 2016, 54: 1212-1239. DOI:10.1016/j.rser.2015.10.042 (  0) 0) |
| [23] |
Aghayari R, Jahanizadeh S, Arani J B, et al. Heat transfer of iron oxide nanofluid in a double pipe heat exchanger. Journal of Materials Science & Surface Engineering, 2015, 2(1): 84-89. (  0) 0) |
| [24] |
Ravi Kumar N T, Syam Sundar L, Bhramara P. Numerical analysis of Fe3O4 nanofluid flow in a double pipe U-Bend heat exchanger. Internaltional Journal of Engineering Studies, 2016, 8(2): 211-224. (  0) 0) |
| [25] |
Zarda F, Hussein A, Danook S, et al. Enhancement of thermal efficiency of nanofluid flows in a flat solar collector using CFD. Diagnostyka, 2022, 23(4): 1-9. DOI:10.29354/diag/156384 (  0) 0) |
| [26] |
Barzegarian R, Aloueyan A, Yousefi T. Thermal performance augmentation using water based Al2O3-gamma nanofluid in a horizontal shell and tube heat exchanger under forced circulation. International Communications in Heat and Mass Transfer, 2017, 86: 52-59. DOI:10.1016/j.icheatmasstransfer.2017.05.021 (  0) 0) |
| [27] |
Hussein Adnan M, Bakar R A, Kadirgama K, et al. Heat transfer enhancement using nanofluids in an automotive cooling system. International Communications in Heat and Mass Transfer, 2014, 53: 195-202. DOI:10.1016/j.icheatmasstransfer.2014.01.003 (  0) 0) |
| [28] |
Rabienataj Darzi A A, Farhadi M, Sedighi K. Heat transfer and flow characteristics of Al2O3/water nanofluid in a double tube heat exchanger. International Communications in Heat and Mass Transfer, 2013, 47: 105-112. DOI:10.1016/j.icheatmasstransfer.2013.06.003 (  0) 0) |
| [29] |
Said Z, Rahman S M A, El Haj Assad M, et al. Heat transfer enhancement and life cycle analysis of a shell-and-tube heat exchanger using stable CuO/water nanofluid. Sustainable Energy Technologies and Assessments, 2019, 31: 306-317. DOI:10.1016/j.seta.2018.12.020 (  0) 0) |
| [30] |
Fares M, AL-Mayyyahi M, AL-Saad M. Heat transfer analysis of a shell and tube heat exchanger operated with graphene nanofluids. Case Studies in Thermal Engineering, 2020, 18: 100584. DOI:10.1016/j.csite.2020.100584 (  0) 0) |
 2023, Vol. 30
2023, Vol. 30


