Binary arithmetic has been popularly used for decades for processing data in computers. It is suitable for many applications, but is not suitable for applications with higher accuracy requirements. This is because conversion from decimal to binary introduces errors for some numbers. For example, numbers such as 0.1, 0.2, etc. cannot be converted into binary with 100% accuracy[1]. Applications in commerce, internet, banking, currency conversion, financial computing, etc. require high accuracy and cannot tolerate even small errors[2-4]. Computation for these kinds of applications is done by using Binary Coded Decimal(BCD) representations. BCD format can be used to represent decimal numbers without any error. Moreover, IEEE 754-2008 standard on floating point arithmetic has also given impetus to research in this area. Many systems such as IBM z900, IBM eServer, IBM z10, Power6, Fujitsu SparcX etc. had already used decimal floating point hardware units[3, 5].
But even with normal BCD representation, there are some limitations. Firstly, it inherently includes the extra 6 representations, i.e. 1010, 1011, 1100, 1101, 1110, and 1111 which complicate the circuits using normal BCD representation. Secondly, it is inefficient in obtaining the 9's complement of a decimal number. Unconventional BCD representations such as BCD-4221 overcome these problems. First of all, it eliminates the extra 6 representations, i.e. 1010-1111, since the total weightage of all the four bits is 9. Although, there are some decimal digits for which multiple representations are possible as shown in Table 1. Furthermore, it is easier to obtain 9's complement using BCD-4221 representation. This is because we can get 9's complement of a number just by inverting all the bits of BCD-4221 representation whereas it requires subtraction from 9 in the case of normal BCD numbers.
| Table 1 Decimal representations |
Now, among all decimal arithmetic operations, decimal addition is the most commonly used. It also forms a basic unit for performing multiplication. Many researchers have worked to design and improve the hardware for performing decimal addition. As addition also forms an integral part of the multiplication process, so, improving the addition part also helps in improving the multiplication process. Also, adder trees are used in reducing Partial Products(PPs). Decimal carry save adder trees are used for reducing the PPs in iterative decimal multipliers[6] and parallel decimal multipliers[7-8]. Alternatively, binary carry-save adders can be used also but with a correction logic, which has been demonstrated for iterative[9] and parallel[10] PP reduction & multi-operand decimal addition[11-13]. Apart from reducing the PPs, adders are also used in obtaining the final sum of the partial products by adding the last two remaining operands. This is generally done by using a carry propagate adder.
Most of the above-mentioned adders use semi-redundant addition where one of the operands is redundant while the other one is non-redundant. However, fully redundant adders had also been proposed, such as Refs.[14-22]. Hence, we are motivated to design a BCD adder that can be used to produce the final sum of PPR numbers available in BCD-4221 format. Our contribution includes:
·Developing a method and logical equations for performing BCD-4221 addition.
·Design of the VLSI hardware circuit for BCD-4221 adder based on the developed approach.
1 Related WorkSeveral authors have given their contributions to the development of decimal adders. Erle and Schulte[6] proposed decimal carry-save addition to reduce the critical path delay. Dadda[12] has worked on the issue of the multi-operand parallel decimal addition process by using an approach that uses binary arithmetic concepts. The binary-to-decimal conversion approach over performing corrections was preferred in order to obtain the result in BCD format. Fast operation and smaller area consumption have been claimed by the authors. Vázquez et al.[10] have presented several techniques for decimal parallel multiplication scheme in hardware which also involved the construction of p∶2 decimal carry-save adder trees that gives interesting area-delay figures. Gorgin and Jaberipur[3] have proposed a novel method for carry-free addition on decimal numbers. The proposed adder is fully redundant in nature and uses an overloaded decimal digit set. Kaivani et al.[17] have also proposed a fully redundant adder which is based on a new redundant decimal digit set [-8, 9] where the transfer digit is stored along with the next higher weighted digit. This transfer digit was produced through a carry-free addition algorithm. A novel BCD-4221 adder proposed by Zhu et al.[19] was used to design a BCD-4221 based multiplier although the multiplier also used several other blocks. The authors synthesized their design in 90 nm technology and concluded that their designs were efficient in terms of area, delay, and power. Mukkamala et al.[20] have worked on BCD adders and converters that are used in parallel implementation of Urdhva-Triyakbhyam based BCD multiplier. They have synthesized their design in field programmable gate arrays (FPGAs) and application specific integrated circuits(ASICs) both, and claimed improvement in delay. Saha et al.[21] have also worked on BCD-4221 based decimal multipliers. They have proposed novel compressors and adders suitable for the design of multipliers. Their implementation results also show delay improvement over other designs. Moskal et al.[22] have also presented an efficient architecture for a multidigit decimal addition. Their adder is based on carry-free signed digit numbers and they claim improvement in area-delay product parameter.
The rest of the paper is presented as follows: We discuss the developed approach and the proposed hardware design details in Section 2. The evaluation and comparison with other adders are presented in Section 3. Finally, we conclude in Section 4.
2 Proposed Redundant Decimal AdderThe proposed redundant adder adds two BCD-4221 numbers and produces the result in the same format. A BCD-4221 format decimal number represents the number with a weightage of 4, 2, 2, and 1 instead of 8, 4, 2 & 1 for one-digit representation. Since the numbers are in BCD-4221 format, they cannot be added by normal binary addition rules. So, in this case, it must include some other blocks which will perform the additional functions of getting the correct result in proper BCD-4221 format. Table 1 shows the conversion table between BCD8421 and BCD4221 formats. It can be observed that decimal digits 2, 3, 4, 5, 6, and 7 have more than one representation in BCD-4221 format. For our proposed adder, we have used the left part of the BCD-4221 representation from Table 1.
2.1 Method & Architecture 1-digit BCD-4221 AdderWhen we add two decimal digits in BCD-4221 format, we get the correct result in some cases, and incorrect results in others. The result is also assumed to be coming in BCD-4221 format. For a total of 10 different digits, the total number of different cases comes out to be 200, i.e., 100 cases with an input carry of 0 and 100 cases with an input carry of 1.
Two patterns are observed while adding two BCD-4221 digits. These are listed below:
1) 1st Pattern. This comprises those combinations for which correct results are coming. Fig. 1 shows some of the examples giving correct results. Correct results come for the combinations of (1, 1), (1, 2), (1, 4), (1, 5), (1, 6), (1, 8), (1, 9), (2, 4), (2, 5), (2, 8), (2, 9), (3, 4), (3, 8), (3, 9), (5, 9), (6, 8), (6, 9), (7, 8), (7, 9) and (9, 9). Obviously, cases like (1, 4) and (4, 1) are assumed to be the same. So, neglecting these overlapping cases, there are a total of 20 such cases for which results are coming correct.

|
Fig.1 Some examples of the addition of BCD-4221 digits yielding correct results |
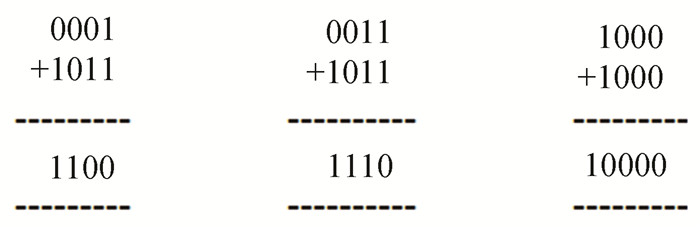
2) 2nd Pattern. There are combinations for which incorrect results are obtained. Some examples are shown in Fig. 2.
|
Fig.2 Some examples of the addition of BCD-4221 digits yielding incorrect results |
Incorrect results occur for the combinations of (1, 7), (2, 3), (2, 6), (3, 1), (3, 2), (3, 3), (3, 5), (3, 6), (3, 7), (4, 4), (4, 5), (4, 6), (4, 8), (4, 9), (5, 3), (5, 5), (5, 6), (5, 7), (5, 8), (6, 6), (6, 7), (7, 7), (8, 8) & (8, 9). While observing the pattern of answers of each addition, we find three different scenarios.First, the result is less by 2 from the actual sum; second, the result is more by 2 for some cases; and third, there are very few specific cases which do not belong to previous two cases. Based on the above observation, we designed three different blocks to handle the incorrect results.
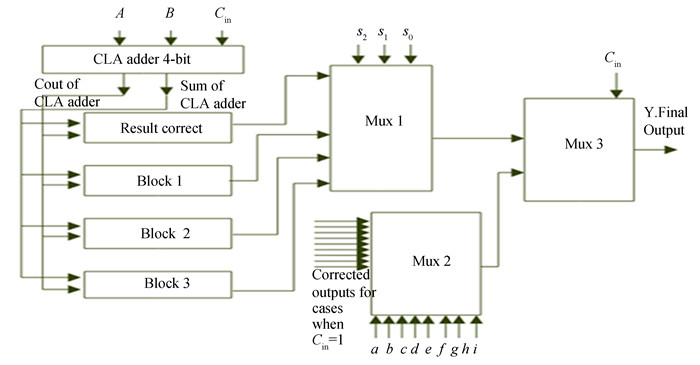
The complete block diagram for a 1-digit BCD-4221 adder is shown in Fig. 3. It contains a one-digit Carry Lookahead Adder (CLA) which performs the normal addition of two digits. The operands A and B are in BCD-4221 format and are 4-bit wide each. Cin is the 1-bit carry input signal. The 1-bit select lines s2, s1, and s0 to Mux1 block come from carry out of CLA and block 3 present in the Fig. 3. The signals a, b, c, d, e, f, g, h and i to Mux2 block are all 1-bit control signals generated from A, B and Cin inputs for selecting some cases of corrected output when Cin is 1. These cases are special cases which are not being produced by CLA and Blocks 1, 2 and 3. These extra processing blocks come from the patterns described above. They result in three blocks, as shown, Block 1, Block 2 and Block 3. These blocks are described below.
|
Fig.3 Architecture for 1-digit BCD-4221 adder |
2.1.1 Block 1
This block adds 2 to those results which are less than by two than the actual answer. A few of the cases coming under this block are shown in Fig. 4.
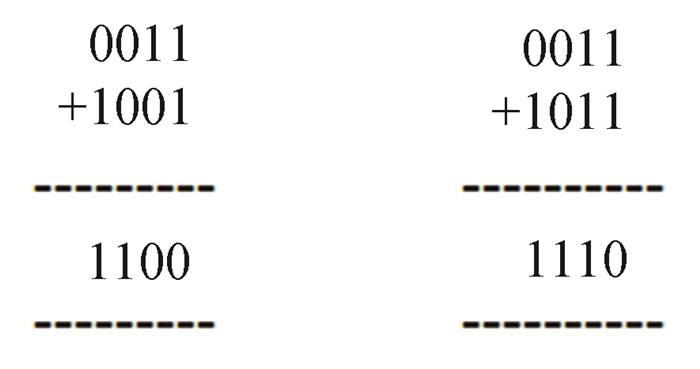
|
Fig.4 Some examples when the result is less than 2 by actual value |
A total of 5 such conditions arise where the yielding result is less than 2 by actual value. The logical equations for this block were obtained by using the k-map reduction method. These are shown in Eqs.(1) -(5),
| $ y_0=a_0 $ | (1) |
| $ y_1=a_3 \cdot a_2 \cdot a_1^{\prime}+a_3^{\prime} \cdot a_2 \cdot a_1 \cdot a_0 $ | (2) |
| $ y_2=a_3 \cdot a_2 \cdot a_1^{\prime} $ | (3) |
| $ y_3=a_2 \cdot a_1^{\prime}+a_3^{\prime} \cdot a_2 \cdot a_0^{\prime} $ | (4) |
| $ y_4=a_3 \cdot a_2 \cdot a_1 \cdot a_0^{\prime} $ | (5) |
The answer is computed by block 2 when the operands are greater than 3. A total of 15 such cases are handled by this block. This takes care of those cases for which the actual result is less than the computed result by 2. Some examples of this block are given below in Fig. 5
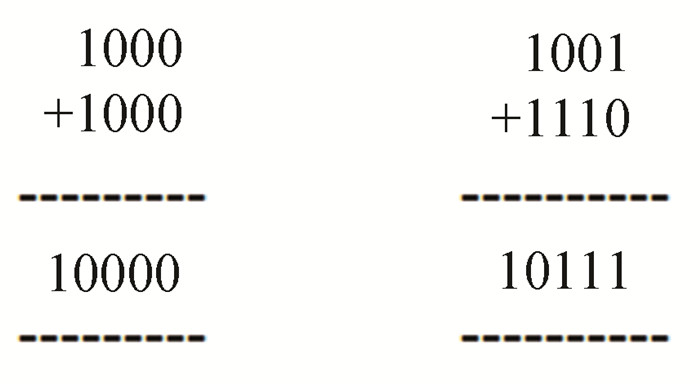
|
Fig.5 Some examples of when the operand is greater than 3 |
Out of these 15 cases, there are two cases for which the same output is coming for different input digits. This is happening for cases (4, 8) & (7, 7). Hence (7, 7) case is not considered for this k-map reduction and is considered in a separate block. After k-map reduction, we get the equations as shown in Eqs. (6)-(10),
| $ y_0=a_0 $ | (6) |
| $ \begin{aligned} y_1= & a_4 \cdot a_3^{\prime} \cdot a_1^{\prime}+a_4 \cdot a_3^{\prime} \cdot a_2+ \\ & a_4 \cdot a_2 \cdot a_1^{\prime}+a_4 \cdot a_3 \cdot a_1 \cdot a_0^{\prime} \end{aligned} $ | (7) |
| $ y_2=a_4 \cdot a_3^{\prime} \cdot a_2^{\prime} \cdot a_1^{\prime} $ | (8) |
| $ \begin{aligned} y_1= & a_4 \cdot a_3^{\prime} \cdot a_2^{\prime} \cdot a_1^{\prime}+a_4 \cdot a_3 \cdot a_1^{\prime}+ \\ & a_4 \cdot a_3 \cdot a_0^{\prime} \end{aligned} $ | (9) |
| $ \begin{aligned} y_4= & a_4 \cdot a_2 \cdot a_1^{\prime}+a_4 \cdot a_3^{\prime} \cdot a_1+ \\ & a_4 \cdot a_3 \cdot a_1^{\prime}+a_4 \cdot a_1 \cdot a_0^{\prime} \end{aligned} $ | (10) |
The case of (7, 7), which was not considered in block 2, is taken here. When we add 7 with 7 in BCD-4221 format, the output coming is 10110, which is wrong. The correct output should be 11000. This can easily be done by performing an inversion at bit positions 1, 2 & 3 considering the start bit position to be 0. But before performing this operation, we should be able to detect if the inputs are (7, 7). This detection will act as a control signal to operate block 3.
2.1.4 Multiplexer 1(for carry in 0)Multiplexer 1, which is active for an input carry of 0, has 3 select lines and 4 inputs. Obviously, one of the inputs comes directly from the CLA adder output. The other three inputs come from the blocks 1, 2 & 3 outputs. Proper input signals are passed on to the output of the multiplexer depending on the control signal values. Correct output is passed by multiplexer by observing the generated signal, G=A & B. Block 1 output will be passed if exclusive-OR of carry at bit positions 2 & 3 is high.
2.1.5 Multiplexer 2(for carry in 1)When input carry is 1, there are 9 cases for which the calculated output is incorrect. And also, at the same time, these cases do not follow any specific pattern. Hence, they are directly fed to multiplexer 2. Correct results are derived from these 9 incorrect results, then fed to the multiplexer inputs, and with proper matching with the select signals, they are passed through the multiplexer to the output. One-hot coding style is chosen for forming 9 select lines for this multiplexer.
2.1.6 Final multiplexer 3All the cases are covered by previous multiplexers 1 & 2. Now, for selecting the final correct result, one last multiplexer is required which will take the inputs from multiplexers 1 & 2 and can pass it on to the output depending on the value of input carry. The output of multiplexer 1 is selected for input carry 0 and the output of multiplexer 2 is selected for input carry 1. The output of this multiplexer is taken as the final output.
2.2 Higher Digit BCD-4221 AdderThe higher digit BCD-4221 adder is formed by using lower digit adders. Since the design is modular in nature, higher digit adders were formed by using lower digit adders. For example, a 4-digit BCD-4221 adder is formed by using four 1-digit BCD-4221 adders. The carry-out of the first adder goes into the carry input of the second adder and so on. Once we form the 4-digit adder, two such adders are used to form an 8-digit adder. And finally, these 8-digit adders are used to form a 16-digit adder(as shown in Fig. 6).

|
Fig.6 Block diagram for (a) 8-digit, (b) 16-digit BCD-4221 adder |
3 Evaluation & Comparison
In this section, we present the evaluation of the proposed design. The results for 1, 4, 8 & 16 digit BCD-4221 adder are obtained. The design is coded in VerilogHDL in structural modeling style. Testbenches were created to verify these designs exhaustively. Designs were verified by performing functional verification in Xilinx Vivado 2016.1. After verifying the functionality of the design, synthesis was done using Cadence Genus16.1 synthesis tool using 90 nm standard cell library. The tool requires the design file in Verilog, a library file for 90 nm, a constraints file, and a tcl file as inputs for producing results. Generally, the synthesis process consists of several intermediate steps such as parsing, elaboration, translation, and optimization of the circuit. After these steps, a netlist in terms of generic gates is produced. This netlist serves as a base for the calculation of performance parameters such as area, power, and delay. Thereafter reports are produced based on these calculations. Table 2 shows the synthesis results for all the blocks used in the proposed circuit.
| Table 2 Synthesis result of components of BC-4221 adder |
It is visible from the table that most of the area and power are consumed by the CLA adder block. It consumes around 58% of the total area and approximately 63% of the total power consumed. It was expected that this block would be more complex than other blocks.
Fig. 7 shows the simulated waveform for a 1-digit adder. All the values are in BCD-4221 format. A 1-digit(4-bit) Carry Look Ahead(CLA) adder is used as the basic design to form higher-digit adders. This can be referred to in Fig. 3. CLA adder is chosen as it is one of the fastest adders for small-size operands.
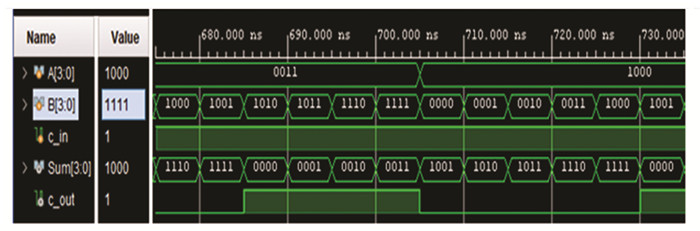
|
Fig.7 Simulation result for 1-digit BCD-4221 adder |
The hardware implementation of the adder is shown in Fig. 8. Basys3 FPGA board was used for testing the BCD-4221 adder. Because of limitation of number of pins on this board, we designed a 1-digit BCD-4221 adder. The programming of Basys3 FPGA board was done by Xilinx Vivado2016.1 tool. In addition to the design file, the tool required a constraint file for mapping the design to the respective FPGA board. The constraint file can be created by performing proper I/O planning with respect to the FPGA board to be used. For example, we have mapped A[3] pin to R2 switch on the board. Similarly T1, U1 and W2 switches are used for mapping A[2], A[1] and A[0] input signals. Also, input signal B is mapped to switches R3, T2, T3, and V2 on the board. Lastly, carry input signal, Cin is mapped to W13 switch. After assigning switches to the input signals, LEDs are assigned to the output signals to observe the outputs. So, output signal Sum and carry-out signal, Cout is mapped to LEDs P1, N3, P3, U3 and L1 respectively. The board in Fig. 8 shows the output for A=3, B=1 and Cin=1. We checked the output for various combinations of the inputs. This implementation of 1-digit BCD-4221 adder is showing proper outputs on the board.

|
Fig.8 Hardware testing of BCD-4221 1-digit adder on Basys3 FPGA board |
After designing a 1-digit adder, bigger-digit adders are designed. The design is modular in nature. So, for example, four numbers of 1-digit BCD-4221 adders are used for designing a 4-digit BCD-4221 adder, and so on. Table 3 shows the performance parameters of the 1-, 4-, 8-, and 16-digit BCD4221 adders.
| Table 3 Synthesis result of BCD-4221 adder |
For a 16-digit BCD-4221 adder, the area consumed is 5784 μm2, the power consumed is 3.111 mW and the delay comes out to be 1.9 ns. The increase in values with an increase in adder size is as per expectation.
Table 4 shows the comparison of the performance parameters of the proposed adder with the adders available in the literature. Synthesis results obtained from Cadence Genus16.1 synthesis tool for our proposed design show an area improvement of 51. 64% and 77.04% over Refs.[21] and [22] respectively. Ref. [20] has given area consumption in terms of the number of NAND2x1 gates used. We estimated the area by multiplying it with the area of one NAND2x1 gate. This gave us an area of 5124.25 μm2. Our BCD-4221 adder consumes 12.88% more area compared with the adder presented in Ref. [20].
| Table 4 Comparison of BCD-4221 adders(16-digit) |
Area-delay product(ADP) and Power-delay product(PDP) are two important comparison parameters for VLSI circuits. But, there is always a trade-off between these two parameters. Table 5 shows the ADP parameter comparison with the schemes presented in Refs. [20-22].
| Table 5 Comparison of ADP for various BCD-4221 adders(16-digit) |
ADP of our proposed adder has an improvement of 54.85%, 43.97%, and 14.46% over Refs. [20], [21] and [22] respectively. For example, our architecture has an ADP of 10989.6 whereas Ref. [20] has an ADP of 24340.1875. This shows that our adder has less ADP compared to Ref. [20]. A similar trend is visible concerning the adders presented in Refs. [21] and [22]. As far as the power-delay product (PDP) is considered it comes as 2.722, 7.7, and 5.91 for Ref. [20], Ref. [22], and the proposed design respectively. Based on PDP values our design performs better than the design of Ref. [22], but at the same time, we observe that the design of Ref. [20] performs better than our design. This may be possible since our primary concern is making the design efficient in terms of ADP parameter.
4 ConclusionsIn this paper, we presented a method to perform the addition of unconventional BCD numbers. The proposed adder is efficient in terms of area and ADP. Such designs with low ADP are desired in the design of decimal floating point arithmetic unit. We have compared our design with previously reported decimal adders. Evaluation and comparison of our adder architecture with others show an ADP improvement of 54.85%, 43.97%, and 14.46%, over Refs. [20], [21], and [22] respectively. So, our design gives an attractive alternative for an area and ADP-efficient BCD4221 adder. In the future, the usefulness of the proposed adder architecture can be studied in applications such as multipliers, fused multiply-add units, dividers etc.
| [1] |
Wahba A A, Fahmy H A H. Area efficient and fast combined binary/decimal floating point Fused multiply add unit. IEEE Transctions on Computers, 2017, 66: 226-239. DOI:10.1109/TC.2016.2584067 (  0) 0) |
| [2] |
Han L, Zhang H, Ko S B. Area and power efficient decimal carry-free adder. Electronics Letters, 2015, 51: 1852-1854. DOI:10.1049/el.2015.0786 (  0) 0) |
| [3] |
Gorgin S, Jaberipur G. A fully redundant decimal adder and its application in parallel decimal multipliers. Microelectronics Journal, 2009, 40(10): 1471-1481. DOI:10.1016/j.mejo.2009.07.002 (  0) 0) |
| [4] |
Cowlishaw M F. Decimal floating-point: algorism for computers. Proceedings 2003 16th IEEE Symposium on Computer Arithmetic, Santiago de Compostela. Piscataway: IEEE, 2003. 104-111. DOI: 10.1109/ARITH.2003.1207666.
(  0) 0) |
| [5] |
Vázquez A, Antelo E, Bruguera J D. Fast radix-10 multiplication using redundant BCD codes. IEEE Transactions on Computers, 2014, 63(8): 1902-1914. DOI:10.1109/TC.2014.2315626 (  0) 0) |
| [6] |
Erle M A, Schulte M J. Decimal multiplication via carry-save addition.Proceedings IEEE International Conference on Application-Specific Systems, Architectures, and Processors. ASAP 2003, The Hague, Netherlands.Piscataway: IEEE, 2003.348-358.DOI: 10.1109/ASAP.2003.1212858.
(  0) 0) |
| [7] |
Lang T, Nannarelli A. A radix-10 combinational multiplier. Proceedings of the 2006 Fortieth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 2006. 313-317. DOI: 10.1109/ACSSC.2006.354758.
(  0) 0) |
| [8] |
Ghose D, Kumar D, Pradhan M. Comparative Analysis of Decimal Fixed-Point Parallel Multipliers Using Signed Digit Radix-4, 5 and 10 Encodings. Recent Trends in Electronics and Communication, 2022, 345-353. DOI:10.1007/978-981-16-2761-3_32 (  0) 0) |
| [9] |
Kenney R D, Schulte M J, Erle M A. A high-frequency decimal multiplier. IEEE International Conference on Computer Design: VLSI in Computers and Processors, 2004. ICCD 2004. Proceedings. San Jose, CA, USA. Piscataway: IEEE, 2004. 26-29. DOI: 10.1109/ICCD.2004.1347893.
(  0) 0) |
| [10] |
Vázquez A, Antelo E, Montuschi P. A new family of high-Performance parallel decimal multipliers. Proceedings of the 18th IEEE Symposium on Computer Arithmetic (ARITH'07), Montpellier, France. Piscataway: IEEE, 2007.195-204.DOI: 10.1109/ARITH.2007.6.
(  0) 0) |
| [11] |
Kenney R D, Schulte M J, Member S. High-speed multioperand decimal adders. IEEE Transactions on Computers, 2005, 54(8): 953-963. DOI:10.1109/TC.2005.129 (  0) 0) |
| [12] |
Dadda L. Multioperand parallel decimal adder: A mixed binary and BCD approach. IEEE Transactions on Computers, 2007, 56(10): 1320-1328. DOI:10.1109/TC.2007.1067 (  0) 0) |
| [13] |
Castellanos I D, Stine J E. Compressor trees for decimal partial product reduction.GLSVLSI'08: Proceedings of the 18th ACM Great Lakes symposium on VLSI. New York: Association for Computing Machinery, 2008.107-110. DOI: 10.1145/1366110.1366137.
(  0) 0) |
| [14] |
Svoboda A. Decimal adder with signed digit arithmetic. IEEE Transactions on Computers, 1969, C-18(3): 212-251. DOI:10.1109/T-C.1969.222633 (  0) 0) |
| [15] |
Shirazi B, Yun D Y Y, Zhang C N. RBCD: Redundant binary coded decimal adder.IEE Proc. E Comp. Digital Tech., Piscataway: IEEE, 1989.36.DOI: 10.1049/IP-E.1989.0021.
(  0) 0) |
| [16] |
Nikmehr H, Phillips B, Lim C C. A decimal carry-free adder. Proceedings of the SPIE-The International Society for Optical Engineering. Bellevue: SPIE, 2004.786-797.DOI: 10.1117/12.584722.
(  0) 0) |
| [17] |
Kaivani A, Jaberipur G. Fully redundant decimal addition and subtraction using stored-unibit encoding. Integration, 2010, 43(1): 34-41. DOI:10.1016/j.vlsi.2009.04.001 (  0) 0) |
| [18] |
Sahu S R, Bhoi B K, Pradhan M. Improved redundant binary adder realization in FPGA. Journal of Circuits Systems and Computers, 2021, 30(16): 2150287. DOI:10.1142/S021812662150287X (  0) 0) |
| [19] |
Zhu M, Baker A M, Jiang Y. On a parallel decimal multiplier based on hybrid 8421-5421 BCD recoding. Proceedings of the 2013 IEEE 56th International Midwest Symposium on Circuits and Systems (MWSCAS), Columbus, OH, USA. Piscataway: IEEE, 2013. 1391-1394. DOI: 10.1109/MWSCAS.2013.6674916.
(  0) 0) |
| [20] |
Mukkamala S, Rathore P K, Peesapati R. Decimal multiplication using compressor based-BCD to binary converter. Engineering Science and Technology an International Journal, 2018, 21(1): 1-6. DOI:10.1016/j.jestch.2018.01.003 (  0) 0) |
| [21] |
Saha P, Samanta P. Investigations on decimal multiplieros through novel partial product generators. Journal of The Institution of Engineers (India) Series B, 2021, 103(7): 507-516. DOI:10.1007/s40031-021-00657-8 (  0) 0) |
| [22] |
Moskal J, Oruklu E, Saniie J. Design and synthesis of a carry-free signed-digit decimal adder. Proceedings of the 2007 IEEE International Symposium on Circuits and Systems, New Orleans, LA, USA. Piscataway: IEEE, 2007.1089-1092.DOI: 10.1109/ISCAS.2007.378199.
(  0) 0) |
 2024, Vol. 31
2024, Vol. 31


