中国医用缝合线每年约有15 亿元人民币的市场需求,其中可吸收缝合线约有7.5 亿元[1-3].可吸收缝合线采用生物材料,或将高分子材料与生物材料结合,主要用于人工器官、外科修复、理疗康复、治疗疾患等[4-5].胶原蛋白与壳聚糖相结合的材料以其毒性小、组织反应小、吸收性好等优点,成为研究的热点之一[6-7].
胶原蛋白与壳聚糖复合流体是一种典型的非牛顿流体,其非牛顿流体指数、粘流活化能和结构粘度指数受混合液的配比,混合液温度等多方面因素影响.例如,随着胶原蛋白含量的增加,混合液的非牛顿性减弱,粘度降低,溶液的非牛顿指数n增加;温度变化引起其粘度变化,从而影响其成型过程.目前由于缺乏对材料的成型机理及纺丝工艺关键技术的掌握,致使成品丝直径不能精确控制,制作出的缝合线线径粗细不均、抗张强度不均,严重影响到临床应用.
本文从胶原蛋白与壳聚糖复合流体的成型规律分析入手,确定喷丝直径与喷丝速度、喷丝针头孔径、流体密度、流体黏度的关系,并在此基础上对缝合线纺丝成型的关键工艺参数进行控制,实现了线径在线非接触测量与闭环控制、缠绕张力闭环控制,从而保证了胶原蛋白与壳聚糖可吸收缝合线的线径和抗张强度的均匀性.
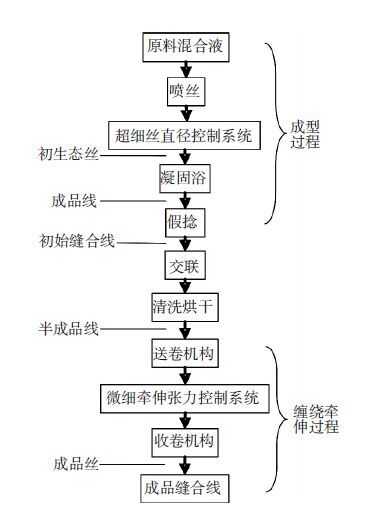
1 胶原蛋白与壳聚糖缝合线的纺丝成型工艺采用JK1601型立管式湿法纺丝机制备胶原蛋白与壳聚糖可吸收缝合线的湿法纺丝制备工艺流程如图 1所示.
|
图 1 可吸收缝合线的纺丝成型工艺流程 Figure 1 Spinning forming process flow of absorbable suture |
原料混合液为胶原蛋白、壳聚糖和蓖麻油按特定配比制作的专利材料,前期采用该材料制作的缝合线的各项性能已经通过天津药品检验所的测试实验,包括化学性能、皮内刺激、植入实验、过敏实验、全身毒性实验等.原料混合液经喷丝机构制成9根直径约为0.1 mm的初生态丝,由线径闭环控制系统控制喷丝机构的喷丝速度,从而控制初生态丝的直径,初生态丝经凝固浴,与凝固液(丙酮、氨水等成分)之间进行双扩散作用,形成成品丝,再经过假捻机构进行加捻和解捻操作,编制成初始缝合线,然后经过交联处理,增加其强度及调节亲水性,经过相应化学处理及清洗烘干后,成为具有一定直径和强度的半成品缝合线,由送卷机构送入带有精细牵伸张力闭环控制的收卷机构,完成成品缝合线的缠绕.在整个湿法纺丝制备工艺过程中,凝固浴、假捻、交联、清洗烘干的工艺过程及工艺参数控制已经达到很好的效果,而成型过程的细丝线径和缠绕牵伸过程的缠绕张力成为制约缝合线制备的2个关键工艺参数.
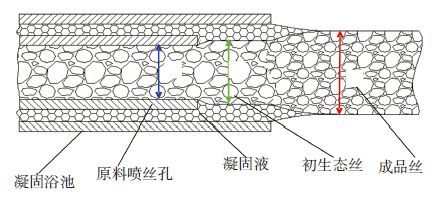
2 胶原蛋白与壳聚糖缝合线成型的有限元分析胶原蛋白与壳聚糖缝合线的喷丝至成品丝的丝径变化过程如图 2所示.
|
图 2 喷丝到成品丝的线径变化 Figure 2 Suture diameter change of Spinning to the finished filament |
胶原蛋白与壳聚糖的原料混合流体在一定压力作用下,由喷丝孔以一定的速度喷出,形成一定直径的初生态丝.由于原料混合液的黏度、喷丝孔出口压力、出口速度等因素的影响,喷丝孔喷出的初生态丝直径d2 与喷丝孔内直径d1 不相等,而是存在一定的数学关系.初生态丝与凝固液(主要成份是丙酮、氨水等)进行酸碱分子的双向扩散,初生态丝中的酸性分子向凝固液中扩散,凝固液中的碱性分子向初生态丝扩散,形成成品丝.成品丝直径d3 与初生态丝直径d2 也不相等,存在一定的数学关系,通过控制凝固液的温度和酸碱度可以保证d3 和d2的比例关系.
本文采用有限元分析的方法[8-10],研究了初生态丝的直径d2与喷丝孔直径d1、原料混合液的黏度、混合液的密度、喷丝孔出口速度等因素之间关系的规律,从而为精确控制成品丝直径d3提供了坚实的理论基础.实验所用复合流体来自天津尚德医疗器械有限公司,由特定配比的胶原蛋白、壳聚糖和蓖麻油材料组成.不同型号的复合流体的密度范围为790~1 210 kg/m3,黏度范围为0.78~1.25 kg/(m·s).
2.1 有限元分析的数学模型利用Gambit软件建立喷嘴模型,如图 3所示.由于喷嘴是轴对称图形,为了减少软件的计算量,只画出了一半的图形.根据生产工艺中常用的喷嘴的尺寸,建模时采用参数:AB=0.015 m,BC=0.015 m,DE=0.03 m,HF=0.029 m,IJ=0.016 m,JK=0.013 m,KL=0.12 m,LM=0.03 m,AG=0.048 m.

|
图 3 喷嘴模型 Figure 3 Nozzle model |
选用5种符合国家标准的喷丝针头孔径,分别是5#:内径0.26 mm,外径0.51 mm.6#:内径0.34 mm,外径0.64 mm.7#:内径0.41 mm,外径0.71 mm.8#:内径0.51 mm,外径0.81 mm.9#:内径0.60 mm,外径0.90 mm.FG为1/2的外径,EG为1/2的内径.
采用Quad四边形网格形式,Submap网格划分类型.计算域边界设置如下:AB为喷嘴入口,设置为速度入口VELOCITY_INLET;EG为喷嘴出口;BCDEFHIJB为喷嘴壁,设置直线BC、CD、DE、EF、FH、HI、IJ、JK为WALL;JKLMGEFHIJ为射流流场外部,设置KL、LM为PRESSURE_OUTLET;AG、GM为轴线,设置AG、GM为AXIS.
有限元分析的数学模型选用VOF模型,根据雷诺数定义
| $\mathsf{Re=}\rho \mathsf{Vd/}\mu $ |
式中:d为喷嘴内直径;V为平均流速;μ为动力学粘性系数.最大喷嘴内径d=0.84 mm,最大喷丝速度V=0.135 m/s,混合液最大密度ρ=1 400 kg/m3,最小动力学粘性系数μ=0.6 kg/(m·s),经计算,喷嘴出口液体流动的最大雷诺数Re=0.264 6<2 000,故选用层流模型Laminar.
入口速度共设定5组值:0.055、0.075、0.095、0.115和0.135 m/s.出口边界条件:采用压力出口,压力设置为0,采用无滑移壁面条件.流体的密度共设定5组值:600、800、1 000、1 200和1 400 kg/m3.流体的黏度共设定5组值:0.6、0.8、1.0、1.2和1.4 kg/(m·s).求解器设定为基于压力的求解器:Pressure-Based.
2.2 仿真结果采用控制变量法,分析了入口速度、流体黏度、流体密度和喷丝针头孔径对射流后流体半径大小的影响.分析数据如表 1~4所示.
| 表 1 入口速度对射流后流体半径大小的影响 Table 1 The influence of inlet velocity on the radius of the fluid after jetting |
| 表 2 流体黏度对射流后流体半径大小的影响 Table 2 The influence of fluid viscosity on the radius of the fluid after jetting |
| 表 3 流体密度对射流后流体半径大小的影响 Table 3 The influence of fluid density on the radius of the fluid after jetting |
| 表 4 喷丝针头孔径对射流后流体半径大小的影响 Table 4 The influence of needle nozzle aperture on the radius of the fluid after jetting |
由表 1~4可以看出:当其他条件不变时,射流后流体半径随入口速度的增大而减少,随流体黏度的增大而减小;随流体密度的增大而增大;随喷丝针头孔径的增大而增大.
将分析结果与JK1601型立管式湿法纺丝机的实验结果相比较表明,仿真分析得出的结论是正确的;在混合液的流体黏度、流体密度和喷丝针头孔径确定的情况下,通过控制喷丝机构的喷丝速度来控制缝合线的线径是可行的.
3 胶原蛋白与壳聚糖缝合线纺丝关键工艺参数控制胶原蛋白与壳聚糖缝合线纺丝工艺的关键参数包括初生态丝的线径、交联液温度和烘干箱温度、凝固液的酸度、缠绕过程的牵伸张力等.线径与抗张强度是缝合线规格的主要性能指标,下面重点介绍这2个指标的工艺参数的控制:线径闭环控制和缠绕张力闭环控制.
3.1 缠绕张力闭环控制 3.1.1 缠绕张力控制的原理可吸收缝合线在收卷筒上缠绕时,缠绕张力通过改变缝合线材料中的大分子链排列结构来改变其抗张强度和对缝合线的线径做最后的微调.在一定牵伸张力范围内,随着牵伸力的增加,缝合线的抗张强度会增加.对于超细的缝合线来说,缠绕张力的微小波动就会引起其较大的变形,导致抗张强度不达标及线径不均匀,最终使得缝合线在缝合或伤口愈合过程中在抗张强度小的地方断裂,影响临床使用效果.
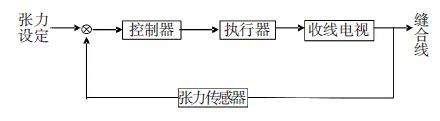
微张力闭环控制系统结构如图 4所示,由传感器、控制器、执行器和人机界面组成.控制器采用欧姆龙CP1H-XA型PLC,包括4路模拟量输入和2路模拟量输出信号,总体测量精度达千分之一.执行器为变频器驱动的变频电机,PLC输出信号为4~20 mA的电流信号,通过变频器转换成交流电压的频率信号,可调范围为0~60 Hz,控制缠绕电机的转速和拨线杆牵引电机的转速,拨线杆的作用是左右拨动送线,保证缝合线在收卷筒上一层一层地铺放,其与缠绕电机的转速相匹配.选择威纶的MT8070IH触摸屏作为人机操作界面,触摸屏与PLC通过R232串口通信.在触摸屏界面可以实现微张力设定、张力显示、缠绕电机转速显示、PID参数设定,以及进行其他手动控制等.
|
图 4 微张力控制系统结构 Figure 4 Micro tension control system structure |
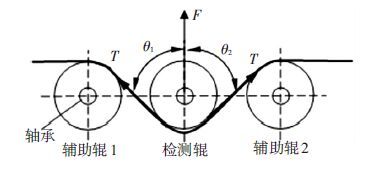
缝合线缠绕过程中的张力控制属于微小张力精确控制,要求精度高.采用电阻应变片式传感器的三辊式测量结构,图 5为三辊式测量结构图,中间是检测辊,左右是辅助辊,起导向作用,被测缝合线绕于3个辊上,将缠绕张力转换为作用在检测辊上的压力,再由传感器进行检测.
|
图 5 三辊张力测量结构图 Figure 5 Structure of tension measurement for 3 rollers |
图 5中,T为缠绕于检测辊上的缝合线缠绕张力,F为施加于检测辊上的总的合力,检测辊的自重可以通过调节传感器的调零功能来消除.它们之间的关系满足欧拉公式:
| $F=2T\cos \left( \theta /2 \right).$ |
式中:θ为检测辊包角,θ=θ1+θ2,θ1=θ2=70°.理论上,F只与T有关,但由于两个辅助辊的内圈和外圈都存在着摩擦,所以选择微型轴承并且其摩擦系数足够小来减少在实际测量中的误差.
电阻应变片式张力传感器作为敏感元件,通过测量电桥和调理电路将应变片的微小电阻变化转化成抗4~20 mA的电流信号,送入PLC,精确调整电路参数,使传感器在小量程0~5 N范围内的测量精度达到±0.05 N.
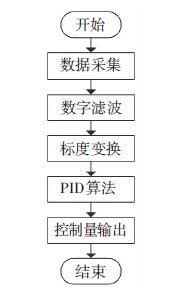
3.1.3 归一化PID控制算法控制算法流程图如图 6,测量数据进入PLC后,首先进行数字滤波和标度变化,滤波采用滑动平均滤波,滤波公式为
|
图 6 控制算法流程图 Figure 6 Control algorithm flow chart |
| ${{y}_{n}}=\frac{1}{N}\sum\limits_{i=0}^{N-1}{{{X}_{n-i}}}.$ |
标度变换采用线性变换,将数字量转换成相应的张力数值,
| ${{A}_{x}}=\left( {{A}_{m}}-{{A}_{0}} \right)\frac{{{N}_{x}}-{{N}_{0}}}{{{N}_{m}}-{{N}_{0}}}+{{A}_{0}}.$ |
归一化PID控制算法公式为
| $\Delta u\left( k \right)={{K}_{p}}\left[ 245e\left( k \right)-3.5e\left( k-1 \right)+1.25e\left( k-2 \right) \right].$ |
经在线PID参数整定,其张力控制范围在0~5 N之间,控制精度达到0.05 N.
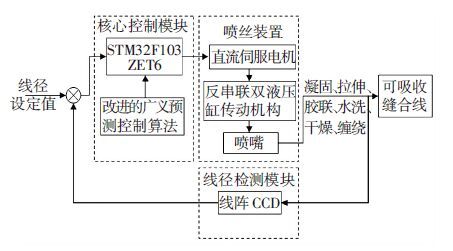
3.2 线径闭环控制可吸收缝合线线径控制系统的总体结构框图如图 7所示.
|
图 7 控制系统总体结构框图 Figure 7 Overall structure diagram of control system |
线径在线测量与闭环控制系统的传感器采用非接触式的线阵CCD传感器[11-12].线径闭环控制系统的控制器采用STM32嵌入式处理器,以线径的检测传感器的输出作为控制器的输入,将线径的测量值与设定值进行比较,对其偏差实行控制算法,算法采用改进的与系统辨识相结合的自适应广义预测控制算法.控制器的输出用来控制喷丝机构的运动速度,通过调整喷丝速度改变喷丝直径.执行器采用串联式的双液压缸来改变喷丝速度.
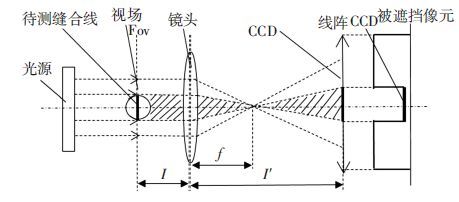
3.2.1 线径在线测量线径测量的光学成像原理如图 8所示. 采用远心平行LED照明光源及远心测量镜头.根据凸透镜成像原理,用平行光源照射缝合线,使其通过镜头成像在CCD上.当CCD的像敏面接收到光信号时,就会根据光束的强弱来产生不同的电荷,通过处理CCD输出的电荷信号来确定CCD像敏面被遮光的尺寸,从而计算出遮光的缝合线直径的尺寸.
|
图 8 系统光学成像原理 Figure 8 Principle diagram of system optical imaging |
线性CCD芯片选用分辨率高、暗电流小的TCD 1209D,该芯片由日本东芝公司生产,其光敏单元数为2 048个,像元大小14 μm×14 μm,最大成像长度为
| $L=2048\times 0.014=28.673\text{mm}\text{.}$ |
根据缝合线制作工艺确定CCD水平视场FOV为4 mm,放大倍率为
| $\beta =\frac{{{I}^{'}}}{I}=\frac{L}{\text{FOV}}=\frac{28.673}{4}\approx 7.17.$ |
测量系统结构如图 9所示.系统以可吸收缝合线作为待测物体,成像在线阵CCD上,由STM32F103ZET6作为控制核心一方面驱动线阵CCD工作,确保CCD输出稳定的电荷信号;一方面对CCD的输出信号进行A/D数据采集,通过软件二值化对图像进行分割,再经过线径计算,最终获得可吸收缝合线的线径测量值.

|
图 9 缝合线线径测量系统结构 Figure 9 Principle diagram of measurement system of suture diameter |
控制算法是决定控制效果的关键因素,经过理论分析和实验探索,针对有一定滞后且系统参数变化较大的湿法纺丝成型机系统,广义预测控制算法(generalized predictive control ,GPC)是理想的控制方案.该模型采用受控自回归积分滑动平均模型(controlled auto-regressive integrated moving average,CARIMA)描述受到随机干扰的被控对象[13-15].
| $\begin{align} & A\left( {{q}^{-1}} \right)y\left( k \right)=B\left( {{q}^{-1}} \right)u\left( k-1 \right)+ \\ & C\left( {{q}^{-1}} \right)\xi \left( k \right)/\Delta . \\ \end{align}$ | (1) |
其中
| $\left\{ \begin{array}{*{35}{l}} A\left( {{q}^{-1}} \right)=1+{{a}_{1}}{{q}^{-1}}+{{a}_{2}}{{q}^{-2}}+\cdots +{{a}_{na}}{{q}^{-na}}, \\ B\left( {{q}^{-1}} \right)={{b}_{0}}+{{b}_{1}}{{q}^{-1}}+{{b}_{2}}{{q}^{-2}}+\cdots +{{b}_{nb}}{{q}^{-nb}}, \\ C\left( {{q}^{-1}} \right)=1+{{c}_{1}}{{q}^{-1}}+{{c}_{2}}{{q}^{-2}}+\cdots +{{c}_{nc}}{{q}^{-nc}}, \\ \Delta =1-{{q}^{-1}}. \\ \end{array} \right.$ | (2) |
式中:u(k)和y(k)分别表示被控对象的输入和输出;q-1是后移算子,即q-1u(k)=u(k-1);q-1y(k)=y(k-1);A(q-1)、B(q-1)和C(q-1)是后移算子q-1的多项式;Δ表示差分算子;ξ(k)是均值为零的白噪声系列.
当被控对象参数未知或时变时,需先在线辨识估计出A(q-1)、B(q-1)、C(q-1)的模型系数.由于缝合线的纺丝成型的工艺复杂,线径检测位置距离喷丝装置较远,喷丝机构是一个液压系统,系统的滞后很大.根据系统的仿真结果,确定系统的初始化参数A(q-1)、B(q-1)、C(q-1),有了初始化参数,再进行系统辨识,可以实现系统辨识结果的快速收敛,达到更好的控制效果.
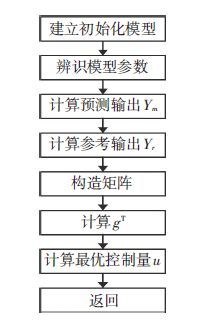
对GPC的基本算法进行了改进,改进后GPC算法减少了控制算法的计算量,提高了控制的实时性;采用了在初始模型参数的基础上在线辨识系统参数的方法,提高了控制算法对系统参数变化的适应能力.改进的广义预测控制算法流程图如图 10所示.
|
图 10 改进的广义预测控制算法流程图 Figure 10 Flow chart of improved generalized predictive control algorithm |
将控制系统安装在JK1601型立管式湿法纺丝机上,分别进行了张力控制实验、线径控制实验、缝合线综合性能实验和比对实验.
4.1 张力控制实验在张力控制实验中,以PLC的系统时钟为计时工具,在稳定纺丝工作过程中,对60 min内的SCX型张力传感器在线实测值进行观察和记录,该传感器的量程为0~5 N,分辨力为0.01 N.实验数据表明,系统能将实际张力值与设定张力值的误差控制在±0.05 N以内,达到恒定张力的控制效果.
4.2 线径控制实验将JK1601型立管式湿法纺丝机生产出的3-0规格的缝合线试样取10根,用TESA MASTER螺旋测微仪在每根试样的1/4,1/2和3/4处进行测量取平均值,结果填入表 5中.
| 表 5 测量结果 Table 5 Measurement results |
实验表明,采用线径控制系统的JK1601型立管式湿法纺丝机生产出的3-0规格的缝合线线径的最大相对误差为3.37%,达到了不均匀性小于5%的设计要求.
4.3 缝合线综合性能缝合线综合性能用来验证缝合线试样的线径和结点抗拉强度是否符合美国药典第35版(USP)中胶原缝合线的标准.
实验中选取2-0和0规格的缝合线试样各取10根,线径的测量方法同实验4.2,结点抗拉强度用电子单纱强力机,标距长度为10 cm,在约6 cm处打结,以280 mm/ min的速度拉断,记录在打结处断裂时的数据,测20个点.上述测量结果填入表 6中.
将表 5、表 6的测量结果与表 7美国药典第35版中胶原缝合线的标准要求相比较,可以看出,应本控制系统的JK1601型立管式湿法纺丝机生产出的2-0、0规格的缝合线线径的线径与结点抗拉强度均符合美国药典第35版标准的要求.
| 表 6 缝合线综合性能测量结果 Table 6 Suture comprehensive performance measurement results |
| 表 7 美国药典第35版标准的要求 Table 7 Requirements of the United States Pharmacopoeia thirty-fifth edition standards |
采用与实验4.3相同的方法,测试在未使用本控制系统的JK1601型立管式湿法纺丝机生产的2-0规格的缝合线样品10根,测量结果见表 8.
| 表 8 未用本控制系统JK1601型纺丝机生产样品的测量结果 Table 8 The measurement results of JK1601 type spinning machine production samples without control system |
通过对表 6与表 8的数据的比对分析,可以看出,在应用本控制系统后,“立管式湿法纺丝机”生产出来的2-0规格的缝合线,直径和抗张强度的不均匀性分别由原来的25.4%、33.2%降低到了4.0%和3.8%.
5 结 论本文提出的胶原蛋白与壳聚糖缝合线纺丝关键工艺参数控制,成功解决了胶原蛋白与壳聚糖材料的可吸收缝合线的精确纺丝成型难题.利用该技术升级改造的“立管式湿法纺丝机”生产出的壳聚糖—胶原蛋白可吸收缝合线样品符合美国药典第35版的要求,直径和抗张强度的不均匀性由原来的25.4%、33.2%降低到5%以内,批量生产后将大大提高其生产质量和生产效率.同时,本文提出的从材料特性及成型规律有限元分析到关键工艺参数控制实现方法,可进一步推广到其他高分子材料的加工、纺织工程、化学工程等各行业中.
| [1] | 中国报告基地.2013-2017年中国医用可吸收缝合线行业市场行情发展趋势及投资前景预测报告[R]. 2013. China report base. China medical absorbable suture industry market trends and investment outlook forecast report 2013-2017[R]. 2013. |
| [2] | 刘小红, 陈向标, 赖明河, 等. 可吸收医用缝合线的研究进展[J]. 合成纤维, 2012, 41 (4) : 23–26. LIU Xiaohong, CHEN Xiangbiao, LAI Minghe, et al. Research progress of absorbable medical suture[J]. Synthetic fiber, 2012, 41 (4) : 23–26. |
| [3] | CHRISTOPHER D, SWAMINATHAN S, SUNITA N, et al. Suture materials-Current and emerging trends[J]. Journal of Biomedical Materials Research, 2016, 104 (6) : 1544–1559. DOI: 10.1002/jbm.a.v104.6 |
| [4] | RUENGDECHAWIWAT S, MOLLOY R, SIRIPITAYANANON J, et al. Synthesis, processing and tensile testing of a poly(l-lactide-co-caprolactone) monofilament fiber for use as an absorbable surgical suture[J]. Macromolecular Symposia, 2015, 354 (1) : 347–353. DOI: 10.1002/masy.201400077 |
| [5] | RUENGDE S, SIRIPITAYANANON J, MOLLOY R, et al. Preparation of a poly(L-lactide-co-caprolactone) copolymer using a novel tin(II) alkoxide initiator and its fiber processing for potential use as an absorbable monofilament surgical suture[J]. International Journal of Polymeric Materials and Polymeric Biomaterials, 2016, 65 (6) : 277–284. DOI: 10.1080/00914037.2015.1119683 |
| [6] | SIONKOWSKA A, KACZMAREK B. Modification of 3D materials based on chitosan and collagen blends by sodium alginate[J]. Molecular Crystals and Liquid Crystals, 2016, 640 (1) : 39–45. DOI: 10.1080/15421406.2016.1255504 |
| [7] | SIONKOWSKA A, LEWANDOWSKA K, GRABSKA S, et al. Physico-chemical properties of three-component mixtures based on chitosan, hyaluronic acid and collagen[J]. Molecular Crystals and Liquid Crystals, 2016, 640 (1) : 21–29. DOI: 10.1080/15421406.2016.1255501 |
| [8] | 吴重敏, 陈革, 薛文良. 基于FLUENT的喷气织机主喷嘴内流场的三维数值模拟[J]. 东华大学学报(自然科学版), 2010, 36 (1) : 66–69. WU Chongmin, CHEN Ge, XUE Wenliang. Numerical simulation of a three-dimensional flow field in main-nozzle of air-jet loom based on fluent[J]. Journal of Donghua University (Natural Science Edition), 2010, 36 (1) : 66–69. |
| [9] | 陈革, 吴重敏, 沈军, 等. 基于Fluent的辅助喷嘴气流流场数值模拟[J]. 纺织学报, 2010, 31 (8) : 122–124. CHEN Ge, WU Chongmin, SHEN Jun, et al. Numerical simulation of flow field of auxiliary nozzle as affected by orifice forms of air-jet loom based on fluent[J]. Journal of Textile Research, 2010, 31 (8) : 122–124. |
| [10] | 郭杰, 冯志华, 曾庭卫. 基于FLUENT的喷气织机主喷嘴内部气流场三维数值分析[J]. 苏州大学学报(工科版), 2009, 29 (2) : 38–42. GUO Jie, FENG Zhihua, ZENG Tingwei. Three dimensional numerical analysis of internal air flow field in the main nozzle of air jet loom[J]. Journal of Suzhow University (Engineering Science Edition), 2009, 29 (2) : 38–42. |
| [11] | 隋修武, 刘蕾, 杜玉红, 等. 基于线阵CCD的可吸收缝合线线径在线检测系统[J]. 传感技术学报, 2014 (8) : 1154–1158. SUI Xiuwu, LIU Lei, DU Yuhong, et al. Online measurement system of absorbable suture diameter based on linear CCD[J]. Chinese Journal of Sensors and Actuators, 2014 (8) : 1154–1158. |
| [12] | QIAO N S, ZHANG F. Method for reducing phase errors due to CCD nonlinearity[J]. Optik, 2016, 127 (13) : 5207–5210. DOI: 10.1016/j.ijleo.2016.03.012 |
| [13] | MANUEL B, MANUEL B, ANTONIO V, et al. On reduction of control effort in feedback linearization GPC strategy applied to a solar furnace[J]. Optimal Control Applications and Methods, 2016, 37 (3) : 521–536. DOI: 10.1002/oca.v37.3 |
| [14] | SHI W G, SHAO C, SUN Z Y. Improved GPC network-control algorithm based on AR model time-delay prediction[J]. Kongzhi yu Juece/Control and Decision, 2012, 27 (3) : 477–480. |
| [15] | SUN L F, SUN J M, MIAO Y D, et al. Application research of PID-GPC algorithm in the ball mill system[J]. Open Automation and Control Systems Journal, 2015, 7 (1) : 157–166. DOI: 10.2174/1874444301507010157 |
 2017, Vol. 25
2017, Vol. 25


