据统计,每年因摩擦磨损造成的经济损失约占一个工业化国家GDP的1%~2%.正因为摩擦磨损与生产和经济密切联系,关于材料摩擦磨损的研究一直是当今多学科的研究热点[1-2].长期以来,关于摩擦磨损的研究大多是通过试验进行的,主要是通过模拟实际工况条件,获得摩擦磨损的特征和变化,从磨损产物、磨损表面状态、摩擦磨损对组织结构的影响等方面来研究各种摩擦磨损的机制和原理[3-5].但这种试验研究不仅耗费大量的人力、物力和财力,还有以下缺点:1) 摩擦磨损是在多因素耦合作用下发生的,任何单一因素对摩擦行为的影响都可能受其他因素的干涉.因此,试验研究很难筛选出影响摩擦磨损的主要因素并定量确定单一因素对摩擦磨损的影响规律.2) 摩擦磨损是一个动态过程,但试验研究很难观察到摩擦磨损过程中的动态变化过程,如位错的移动、应力应变的变化、表层和亚表层的变化等.3) 摩擦磨损实际上是材料表面原子之间键合的破坏,试验研究很难从原子微观角度来揭示摩擦磨损的特性.
随着计算机技术的发展,数值模拟已经成为摩擦学领域研究常用的研究手段[6].作为主要的数值模拟方法之一,分子动力学模拟方法可以通过构造比较理想的模型,定量地再现真实固体中所发生的动态过程,能够很好地弥补实际实验方法的缺陷,还可以根据研究需要轻易地改变周围环境条件和材料的性质.因此,分子动力学模拟已成为摩擦磨损研究的重要手段.目前已经成功应用于超高精密加工、微纳米元器件等研究领域.
本文详细综述了材料摩擦磨损分子动力学模拟的最新研究进展,旨在为材料摩擦磨损研究提供有效方法,进而实现材料摩擦磨损性能的改善和减摩抗磨材料的设计.文章结构如下:第1节介绍了分子动力学模拟中势能函数的建立; 第2节综述了材料摩擦磨损分子动力学模拟常用的接触模型; 第3节重点归纳了接触面积、载荷、温度、速度和晶体取向等因素对材料摩擦磨损分子动力学模拟结果的影响; 第4节指出了目前采用分子动力学模拟方法对材料摩擦磨损进行研究的过程中存在的一些问题,并对未来发展方向进行了初步展望.
1 原子间势能函数模型分子动力学模拟方法的原理是通过原子间的相互作用势,按照经典牛顿运动定律求出原子轨迹及其演化过程.因此,建立合适的势能函数是进行材料摩擦磨损分子动力学模拟的第一步,也是最关键一步.势能函数的正确与否,直接关系到模拟结果的精确性和可靠性.
1.1 经典对势函数经典对势认为原子之间的相互作用是两两之间的作用,与其他粒子无关.这类函数的特点是虽然不能充分反映材料的一些真实性能(弹性模量或者热力学性质),但是能够反映粒子的一般运动轨迹.这类对势函数的典型代表就是L-J势和Morse势.
L-J势函数的表达式为[7]
| ${V_{{\rm{LJ}}}} = 4\varepsilon {\left( {\frac{\sigma }{r}} \right)^{12}} - {\left( {\frac{\sigma }{r}} \right)^6}.$ | (1) |
式中:VLJ为系统势能; ε为能量参数; σ为长度参数; r为2个原子之间的距离.在该表达式中,第1项代表短程泡利排斥力,第2项代表范德瓦尔兹相互吸引力.
L-J势能函数可以用于描述稀有气体之间的相互作用,同样可以用于描述一些其他材料.关于材料摩擦学分子动力学模拟的很多显著发现都是采用L-J势.例如,Luan等[8]采用L-J势建立摩擦模型,预测了适用于宏观摩擦的连续介质模型并不适用于纳观尺度摩擦.Cieplak等[9]采用L-J势建立模型,研究了吸附单层对摩擦的效果.此外当摩擦体系中摩擦副(基体)和对磨材料(压头)的性质不同,且无严重磨损的情况下,L-J势可以很好地描述基体和压头之间的相互作用势[10].这可以帮助绝大多数的摩擦磨损模拟体系在保证模拟结果精确的情况下,减小运行时间,提高运行效率.
对势除了前面提到的L-J势之外,还有Morse势.Morse势是在用量子力学解决双原子分子震动谱时给出的分析式.值得指出的是,L-J势和Morse势的参数可直接由原子之间的平衡距离及结合能来拟合获得.因此这2种势函数对于单质和一些简单的合金材料均适用.
1.2 多体势函数简单对势函数并不能充分反映多原子体系材料的一些真实性能,因此,学者们一直致力于建立能够更准确描述多原子体系相互作用的多体势函数.常用于摩擦磨损的材料主要包含3种:金属晶体,离子晶体和共价晶体.因为组成这3种晶体的键的性质不同,因此其势能函数的建立方法也不尽相同,下面分开讨论这3种材料势能函数的建立.
1.2.1 金属晶体的势能函数对于金属晶体的势函数而言,目前应用最广泛的是BASKES和DAW在1984年提出的嵌入原子法(EAM)理论[7],该理论的基本思想就是将金属晶体总能分为2个部分:一部分就是晶体点阵上原子核之间的相互作用,另一部分是原子核嵌入在电子云背景中的嵌入能.可以表示为
| ${E_{{\rm{tot}}}} = \sum\limits_i {} F{\rm{ }}({\rho _i}) + \frac{1}{2}\sum\limits_{j \ne i} {} \mathit{\Phi }({r_{ij}}).$ | (2) |
式中:Etot为系统的总势能; F表示把原子i嵌入到密度为ρi背景电子云中时的嵌入能; ρi表示原子i处的电子云密度; Φ是原子i和j之间的相互作用对势,rij是原子i和j之间的距离.
式(2) 中, 右边第1项是原子i在周围原子叠加电子云中的嵌入能,第2项是原子核间的对势能.上式对于纯金属和合金材料均适用,只是纯金属和合金材料的两体势函数的表达式不同.
EAM势能函数已经在Pt、Au、Cu、Al和Ag等金属的摩擦磨损分子动力学模拟研究中得到了成功的应用,得到了很多金属的原子尺度摩擦现象,例如:犁沟、切削、冷焊和黏滑[11-13].
EAM势函数的建立是基于电子密度球对称分布.但是这种假设在一些情形下与实际情况偏离,例如d电子轨道不满的过渡族(Fe, Co, Ni)元素,金刚石结构的半导体元素及轨道杂化的体系.为了将EAM推广到共价键和过渡金属材料,必须考虑电子云的非球形对称.于是,Baskes等[14]提出了修正型嵌入原子法(MEAM).该方法是在基体电子密度求和中引入原子电子密度分布的角度依赖因素.
1.2.2 共价晶体的势能函数用于摩擦磨损的另一大类材料是共价晶体.例如SiO2、石墨、金刚石、类金刚石碳和一些氧化物.共价键有2个主要的特征:首先是结合能非常强,其次是有一个显著的方向性.为了准确反映这2个特征,研究者们建立了一种由键长、键角和扭曲度确定的势能函数.这种势能函数的典型代表是S-W模型,该模型提出最初是为了模拟类金刚石结构的Si[15].该模型能够简化原子间相互作用,但是该模型的缺点是只允许存在一种平衡的结构.为克服这一缺点,人们提出了键序势函数,通过引进一个键序参数来评价不同键的强度,因此一个势能函数可以同时描述含不同键合的平衡结构.但是,因为考虑了更多的参数,所以计算量大大增加.键序势能函数的代表是Tersoff势能函数,REBO势能函数,ReaxFF势能函数.
很多共价晶体摩擦的分子动力学模拟都运用了上述势能函数.例如:Li等[16]采用Tersoff函数来描述单晶硅的相互作用势,利用分子动力学模拟方法研究了金刚石压头的切削速度对单晶硅亚表面和表面损伤的影响.Gao等[17]用REBO势能函数描述了氢终端金刚石的势能函数,研究了温度的变化对金刚石-金刚石摩擦磨损的影响.Wen等[18]采用基于ReaxFF势能函数的分子动力学模拟方法研究了水环境中Si/SiO2界面处Si的摩擦磨损机制.
1.2.3 离子晶体的势能函数相比于金属晶体和共价晶体而言,对离子晶体的摩擦磨损分子动力学研究较少.离子晶体中包含2个或者更多的反向带电离子.为了对这些离子键进行模型化,需要用长程库仑力来描述原子间相互作用.但是,长程相互作用大大增加了计算时间,这就限制了分子动力学模拟的粒子数目.尽管对离子晶体摩擦磨损的直接模拟很少,但是已经有一些尝试,例如,Wyder等[19]将每一个离子抽象成由一个正离子和周围的负离子网组成,将短程力和长程力相结合来描述KBr的势函数,研究了KBr (100) 表面的黏滑摩擦现象.
值得说明的是,目前针对一些晶体结构相对简单的一元或者二元化合物的势能函数已经有了很多的报道,而目前针对一些结构相对复杂的三元化合物势能函数鲜有报道.随着新技术的发展,一些具有复杂晶体结构的三元化合物,例如Ti2AlN、Ti3SiC2等,已经成功用于制备抗磨减摩的薄膜材料[20]、陶瓷材料[21]和复合材料[3].因此,为了更好地理解该类化合物的抗磨减摩机制,对该类复杂化合物势能函数的建立也必定是未来的研究方向.
2 摩擦磨损分子动力学接触模型摩擦磨损是2种材料之间的接触行为,因此建立合适的摩擦磨损分子动力学接触模型是获得正确和可靠的模拟结果的前提.目前用于摩擦磨损分子动力学的接触模型主要有平面-平面接触、粗糙峰-平面接触、粗糙峰-单峰接触3种.
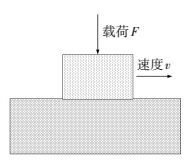
2.1 平面-平面接触模型图 1给出了平面-平面接触模型的示意图.在该模型中,2个原子尺度平面在一定的载荷作用下以速度v彼此滑动.在整个模拟过程中,2个接触平面始终保持全部接触.
|
图 1 平面-平面接触模型示意图 Figure 1 The schematic of flat surface-flat surface interaction |
Jeng等[22]建立了面心立方(111) 晶面的平面-平面接触模型,采用分子动力学模拟的方法研究了“硬-软”、“软-软”2种接触体系的摩擦行为.Kartikeyan等[23]建立了Fe-Cu的平面-平面接触模型,采用分子动力学模拟方法研究了滑移速度、晶体学取向和晶体缺陷对摩擦副摩擦学特性的影响.
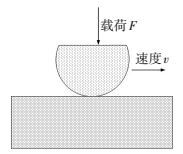
2.2 粗糙峰-平面接触图 2给出了粗糙峰-平面接触模型的示意图.在该模型中,一个粗糙峰在一定的载荷作用下以速度v划过平面.粗糙峰可以有不同的尺寸和形状(球形、半球形、棱柱形、圆柱形).在整个模拟过程中,粗糙峰与平面始终保持接触.
|
图 2 粗糙峰-平面接触模型示意图 Figure 2 The schematic of asperity-flat surface interaction |
在很多研究微纳米器件中的超精密切削的报道中,均采用粗糙峰-平面接触模型.例如,Zhang等[24]采用分子动力学方法模拟金刚石压头在铜基体表面的滑动过程来研究纳米尺度的摩擦磨损规律.Cho等[13]建立了Ni压头与Cu表面的接触模型,采用分子动力学方法研究了原子尺度滑移中的黏滑现象.
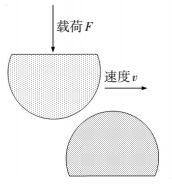
2.3 粗糙峰-粗糙峰接触图 3给出了粗糙峰-粗糙峰接触模型的示意图.在该模型中,一个粗糙峰在一定的载荷作用下以速度v划过另一个粗糙峰.粗糙峰可以有不同的尺寸和形状(球形、半球形、棱柱形、圆柱形).在整个模拟过程中,只测试2个粗糙峰接触时的摩擦学特征.
|
图 3 粗糙峰-粗糙峰接触模型示意图 Figure 3 The schematic of asperity-asperity interaction |
Stone等[25]建立了2个球形纳米Ni颗粒的接触模型,采用分子动力学方法研究了球形纳米Ni颗粒相互滑动过程中的摩擦行为.Luan等[26]建立了粗糙峰-粗糙峰接触模型,采用分子动力学方法研究了压头几何结构对黏着接触和非黏着接触过程中的接触力学.
从以上分析可以看出,研究的材料体系不同,所采用的接触模型也不尽相同.一般来说,在研究纳米尺度摩擦磨损的时候,3种接触模型均适用; 而在研究微纳米器件中的超精密切削时,多采用粗糙峰-平面接触模型.值得指出的是,因为宏观材料摩擦磨损可以看做是许多不同尺度、不同取向的粗糙峰彼此相互作用的结果,所以粗糙峰-粗糙峰接触模型被认为最能真实反映宏观尺度的摩擦磨损.但目前最大的挑战就是粗糙峰的尺寸和数量是多少的时候才能真正反映真实宏观尺寸的表面.这也必定是未来材料摩擦磨损分子动力学研究的重点方向之一.
3 摩擦磨损分子动力学模拟研究进展影响材料摩擦磨损的主要因素包括接触面积、载荷、温度、速度和晶体取向等因素.在实际的试验中,这些因素耦合作用,从而使材料摩擦磨损呈现复杂性.而分子动力学模拟法则可以确定单一因素对材料摩擦磨损的影响,因此本小节的每一部分都将对每个单一因素对材料摩擦磨损的影响进行综述.
3.1 接触面积根据宏观摩擦定律,摩擦力F与接触面积比Amacro无关.但后来学者们证明,宏观尺度的接触是粗糙的,接触表面含有大量的粗糙峰接触,真实接触面积∑Aasp远比Amacro要小很多,摩擦力与真实接触面积成线性关系.目前采用分子动力学模拟的方法对接触面积对材料摩擦磨损的影响的报道已经有很多,但是尚没有形成统一的结论.
一些材料摩擦磨损分子动力学模拟的研究表明,摩擦力与接触面积成正比.例如Gao等[27]建立了金刚石的单峰摩擦分子动力学模型,模拟结果表明在无黏着和有黏着的情况下,摩擦力F与粗糙峰接触面积Aasp均成正比.Mo等[28]建立了多峰纳米接触摩擦分子动力学模型,研究了氢终端的无定形碳探针与氢终端的金刚石之间的摩擦特性,他们定义真实接触面积Areal=NatAat,Nat是界面处有化学相互作用的原子数,Aat是每个原子的平均表面积.Aasp为接触边界.研究结果表明,摩擦力F与粗糙峰接触面积Aasp不成线性关系,而与真实接触面积Areal成正比.值得说明的是,虽然Gao和Mo的研究结果均表明摩擦力与接触面积成正比,但二者对接触面积的定义不同,此外二者运用的理论也不同.Gao等建立的单峰模型中单峰模型可以用连续介质力学理论描述; 而Mo等建立的是多峰纳米接触模型,此时连续介质力学并不适用,需要用原子模型进行解释.
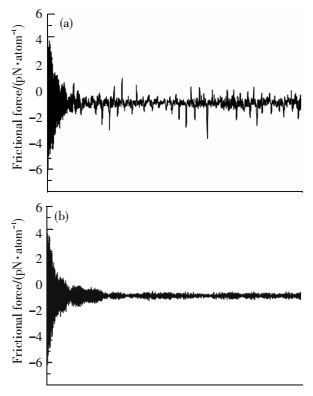
另一些材料摩擦磨损分子动力学模拟研究表明摩擦力与接触面积无关.一些学者们在石墨[29]、MoS2[30]等的摩擦磨损分子动力学模拟过程中均发现了同一现象,如图 4所示,当原子级光滑的理想晶体表面间非公度接触时(即晶格完全适配)时呈现出一种超滑的现象,此时摩擦力几乎为零,因此摩擦力与接触面积无关.而当其为公度接触时,摩擦力随着接触面积的增大而增加.造成这种“超滑”现象的原因是,在非公度接触界面上,每个原子受到的剪切应力方向是不同的,但整体而言,这些力几乎可以相互抵消,因此呈现超滑现象.
|
图 4 MoS2公度接触和非公度接触的摩擦力曲线[30] Figure 4 Frictional force of MoS2 flake/plate contact interface[30]: (a) commensurate contact; (b) non-commensurate contact |
从以上的分析可以看出,接触面积对材料摩擦磨损的影响十分复杂,首先是对接触面积的定义还不统一,所以不同的分子动力学模拟的模型就有着不同的模拟结果; 其次,摩擦力与接触面积之间的关系还取决于其他影响因素,例如表面公度.
3.2 载荷宏观的摩擦定律表明摩擦力为摩擦系数μ与载荷N的乘积,即F =μN.但是当材料摩擦磨损到达原子尺度,黏着变得明显,影响载荷和摩擦力之间关系的因素也增多,因此摩擦力和载荷之间的关系将呈现出明显的复杂性.
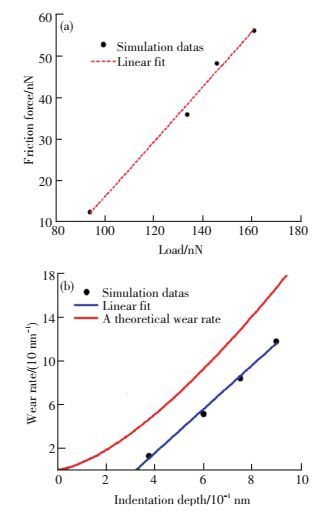
很多材料摩擦磨损分子动力学模拟研究发现摩擦力与法向载荷之间成近似的线性关系.Filleter等[31]采用分子动力学模拟的方法研究了SiC基体外延沉积单层和双层石墨烯薄膜的摩擦行为,研究表明摩擦力与载荷成近似的线性关系.Brukman等[17]采用原子力显微镜(AFM)和分子动力学模拟相结合的方法研究金刚石的单峰摩擦行为.研究结果同样表明,摩擦力与载荷之间成近似的线性关系.Xu等[10]采用分子动力学模拟的方法对半圆球的金刚石在γ-TiAl基体中的纳米压痕和摩擦磨损行为进行研究,如图 5所示,金刚石压头在滑行过程中的摩擦力和磨损率与载荷之间呈线性关系.
|
图 5 金刚石与TiAl之间摩擦力和磨损率与载荷的关系[10] Figure 5 The dependence of frictional force and wear rate between diamond tip and TiAl substrate on the load[10]: (a) relationship between friction force and load; (b) relationship between wear rate and load |
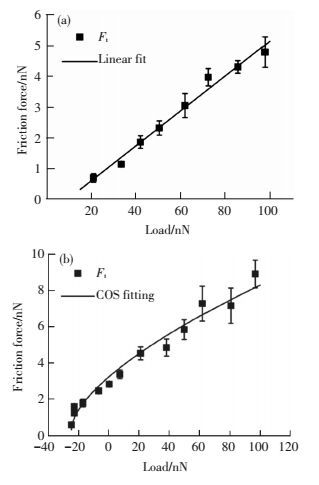
但更多的摩擦磨损分子动力学模拟研究发现摩擦力与法向载荷之间是非线性关系.如图 6所示,Mo等[28]的分子动力学模拟研究发现当氢终端的无定形碳探针与氢终端的金刚石之间无黏着的时候,摩擦力与法向载荷之间呈线性关系,而有较强的黏着力的时候,摩擦力与法向载荷之间呈非线性关系.Van Wijk等[32]采用分子动力学模拟方法研究了石墨烯与石墨之间的摩擦特征发现当表面之间为公度接触时,摩擦力随载荷线性增大,而非公度接触时,在低载荷下摩擦力变化不大,高载荷下摩擦力与载荷呈指数关系.
|
图 6 氢终端的无定形碳探针与氢终端的金刚石之间的摩擦力与法向载荷的关系[28] Figure 6 The dependence of frictional force between an amorphous carbon tip and a diamond sample on the load[28]: (a) non-adhesive contact; (b) adhesive contact |
从以上的分析可以看出,摩擦力与载荷之间的关系主要受材料的本征性质、接触表面间黏附作用、表面接触方式以及塑性变形等的影响,因此,不同的材料以及不同的模拟模型得出的结论也是不一致的.
3.3 温度温度能够对原子的热动能产生明显影响,因此温度对材料的摩擦磨损也会产生显著的作用.受实验设备所限,材料在极端温度(低温、高温)下的摩擦磨损特性尚缺乏系统研究.但是在分子动力学模拟中,可以很容易地控制材料模拟系统中的温度,所以分子动力学方法能够很好地研究温度对材料摩擦磨损的影响.
目前大部分的材料摩擦磨损分子动力学研究表明,随着温度的升高,摩擦力会显著降低.例如,Harrison等[33]通过分子动力学模拟的方法研究了温度对氢终端的金刚石接触表面间摩擦的影响,研究结果表明随着温度的升高,摩擦力降低.Brukman等[17]采用分子动力学模拟的方法研究了温度在24~225 K内变化时对金刚石单峰摩擦行为的影响,研究结果表明,随着温度的升高,摩擦力降低.
但也有一些研究表明系统温度的升高并不会降低摩擦,例如Cook等[34]采用分子动力学模拟方法研究了多壁碳纳米管层间的摩擦行为,研究结果表明,随着温度的升高,层间原子发生非接触碰撞的频率增加,因此增加了层间摩擦力.
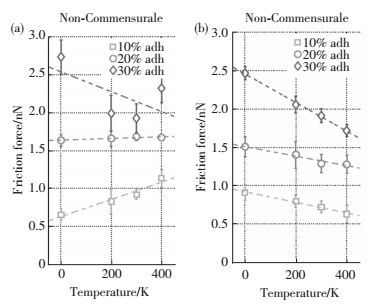
此外还有一些材料摩擦磨损分子动力学模拟报道表明材料的摩擦与接触表面的黏附作用和公度有关.Spijker等[35]采用分子动力学模拟的方法研究了原子尺度下温度与干摩擦之间的关系.研究结果如图 7所示,接触表面为公度的情况下,摩擦力随着温度的升高而降低,但是当接触表面为非公度的情况下,摩擦力随着温度的升高而升高,这主要是因为表面原子的热震荡所致.
|
图 7 面心立方晶体中摩擦力与温度之间的关系[35] Figure 7 The frictional force of face-centered cubic crystal as a function of temperature[35]:(a) non-commensurate contact; (b) commensurate contact |
对于大多数的摩擦过程而言,相对滑移可引起表面层或者亚表面层发热、变形、化学变化甚至磨损,因此,不同的相对速度会对摩擦行为产生显著影响.
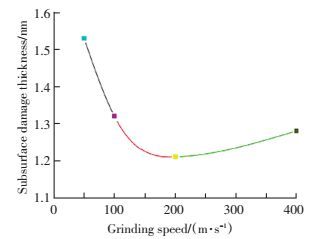
一些摩擦磨损分子动力学模拟研究表明,随着相对速度的增加,摩擦力增大,磨损率增加.例如Li等[11]采用分子动力学方法研究了Au (111) 表面的摩擦特性,发现当相对速度低于某一临界值时,摩擦力随着相对速度的增加而增加,当相对速度超过该临界值时,摩擦力不再随温度的增加而变化.Li等[16]采用分子动力学模拟法研究了金刚石压头的切削速度对单晶硅的切削磨损机制.如图 8所示,当切削速度低于180 m/s的时候,高的切削速度导致一个更大的磨损,降低了亚表面的损伤.但是当切削速度高于180 m/s时,亚表面损伤厚度增加,因为高的切削速度导致了切削力和温度的提高,加速了位错的形核.
|
图 8 单晶硅的亚表面损伤厚度随切削速度的变化曲线[16] Figure 8 Theeffect of grinding speed on the subsurface damage thickness of single crystal silicon[16] |
另外有一些摩擦磨损分子动力学模拟研究表明,随着相对速度的增加,摩擦力降低,磨损率下降.Sørensen等[36]采用分子动力学方法模拟了Cu探针沿着晶体Cu表面的黏滑现象,研究结果如图 9所示,相对速度的增加会使得摩擦力下降.这主要是因为当相对速度很大的时候,变形能没有得到充分的释放,所以为接下来的滑移提供了一些能量,从而降低摩擦.Hu等[37]采用分子动力学模拟的方法研究了滑移表面之间加入Cu纳米颗粒的加入对固体表面摩擦特性的影响,研究结果表明随着相对速度的增加,摩擦力降低.这主要是因为纳米颗粒的加入能够在固体表面形成一个过渡层所致.

|
图 9 面心立方晶体中摩擦力与速度之间的关系[36] Figure 9 The frictional force of face-centered cubic crystal as a function of the sliding velocity[36] |
摩擦现象,归根到底属于2种材料之间的接触力学行为,因此基体的晶体结构、表面原子结构的取向,以及压头与基体之间的取向均会对摩擦产生显著的影响.分子动力学模拟方法在研究晶体取向对摩擦磨损的影响方面有着很大的优势,因此很多学者开展了这方面的研究.
不同的晶体结构,摩擦特性会有明显的不同.例如一些自润滑材料,如石墨、MoS2和无定形碳薄膜等,其自润滑的本质就是其层状的晶体结构.Matsushita等[38]采用分子动力学研究了干净石墨表面之间的原子尺度摩擦,模拟结果表明石墨呈现出在原子尺度黏滑移动和低的摩擦系数.石墨低的摩擦系数的原子尺度起源不仅仅是层与层之间的弱的结合作用,而是因为石墨的蜂巢结构.低的摩擦系数来源于薄片之间2种不同的晶格位置之间力的抵消.Miyamoto等[39]用联合量子化学和经典分子动力学的方法研究了MoS2的润滑机制.他们发现2个S层之间的主导相互作用力是库伦排斥力,直接阻止了2个MoS2层不会靠的太近.也就是MoS2层有一个好的阻止载荷的能力.Ma等[40]采用分子动力学方法研究了无定形碳薄膜与金刚石对磨材料的滑移接触过程中无定形碳薄膜润滑的本质.研究结果表明:经过稳定滑移过程,一个类石墨烯sp2主导层在无定形碳薄膜表面逐步形成.这是因为二轴力的释放导致sp3向sp2结构转变.在石墨化层的形成之后,相对滑移就在石墨化层之间发生.在剪切过程中,双轴力从一个高的压应力(42 GPa)向拉应力(-3 GPa)转变.
不同的晶面,其摩擦特性也会有所不同.Gao等[27]采用分子动力学方法研究了金刚石不同晶面上的摩擦行为,结果表明,金刚石(001) 表面的摩擦力高于(111) 表面.这是因为金刚石(001) 的表面能更高,所以产生更强的黏附作用.同样的现象也在其他面心立方的金属中被发现,例如Li等[41]采用分子动力学方法研究了Pt压头在Au (100) 和Au (111) 晶面的摩擦行为,研究结果表明,Pt压头在Au (100) 晶面摩擦时会有磨损产生,且摩擦曲线不稳定.而当Pt压头在Au (111) 上摩擦时,磨损量相对较少,且摩擦曲线呈现规律的锯齿状.造成这种现象的原因主要是因为Au (111) 晶面的能量比(100) 晶面的能量低,所以黏着力较低,因此摩擦力也相对较低.类似的结果也在Cu等金属中被发现.
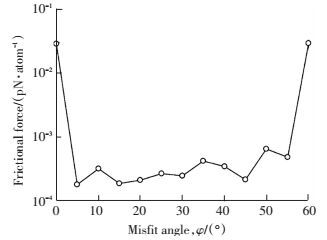
晶面原子结构的取向不同也会导致材料摩擦特性不同.Balakrishna等[42]采用原子力显微镜结合分子动力学模拟的方法研究了石墨表面摩擦的各向异性.Onodera等[30]采用分子动力学方法研究了2个MoS2层之间的摩擦尺度的动态摩擦.研究结果如图 10所示,非公度结构显示出低的摩擦,因为摩擦力在滑移方向上的抵消,导致光滑摩擦.但是在公度结构,所有的原子同时越过对磨原子,导致摩擦力比非公度接触高100倍.
|
图 10 2个MoS2层间摩擦力与层间角度之间的关系[30] Figure 10 Relationship between misfit angle of two MoS2 plates and frictional force[30] |
综上所述,国内外学者对材料摩擦磨损分子动力学模拟进行了很多研究,得到了一些对材料摩擦磨损研究很有意义的结论.从这些模拟结果来看,材料的摩擦磨损受多种因素耦合作用所影响,且原子尺度摩擦和宏观尺度摩擦存在着明显的区别.使得到目前为止仍很难从本质上给出摩擦的起源并归纳出普适的摩擦磨损规律.且对于材料摩擦磨损分子动力学模拟本身而言,仍存在一些缺点:1) 空间尺度和时间尺度有限,模拟的规模小; 2) 势能函数有限,不具备普适性; 3) 模拟条件过于理想化,模拟结果具有局限性.
因此,笔者认为在未来摩擦磨损分子动力学模拟领域研究中,需要在以下几个方向开展重点研究:
1) 加强对一些新型复杂耐磨减摩材料,例如Ti2AlN、Ti3SiC2、Cr2AlC等的摩擦磨损分子动力学模拟研究,从原子尺度阐明其耐磨减摩的内在机制.
2) 研究开发更准确、更普适的新型势能函数,使其能够更加精确地反映材料的性能.尤其是对晶体结构相对复杂的三元化合物等新型摩擦材料的势能函数,更是未来所要研究的重点方向.
3) 建立能够反映真实宏观尺寸表面的摩擦磨损分子动力学模拟的模型.确定在什么控制参数下原子尺度摩擦参数可以收敛到宏观尺度.
4) 加强多尺度模拟的研究,比如分子动力学模拟与有限元方法结合,分子动力学模拟与第一性原理结合,从而扩大模拟系统的尺寸,更精确地解释摩擦磨损的微观机制.
5) 加强材料摩擦磨损分子动力学模拟结果与试验结果之间的相互关联和桥接,完善摩擦学理论.
| [1] | 温诗铸, 黄平. 摩擦学原理[M]. 北京: 清华大学出版社, 2002: 256-354. |
| [2] | 崔海霞, 陈建敏, 周惠娣. 奇妙的摩擦世界[M]. 北京: 科学出版社, 2010: 1-5. |
| [3] | SUN Tao, WANG Qing, SUN Dongli, et al. Study on dry sliding friction and wear properties of Ti2AlN/TiAl composite[J]. Wear, 2010, 268: 693–699. DOI: 10.1016/j.wear.2009.11.007 |
| [4] |
刘渊, 闫洪, 王志伟. 流变成形压力对Al2Y/AZ91镁基复合材料摩擦磨损行为的影响[J]. 材料科学与工艺, 2016, 24(2): 29–35.
LIU Yuan, YAN Hong, WANG Zhiwei. Effects of rheological forming pressure on friction and wear characteristics of Al2Y/AZ91 magnesium matrix composites[J]. Materials Science and Technology, 2016, 24(2): 29–35. DOI: 10.11951/j.issn.1005-0299.20160202 |
| [5] |
程永奇, 汪存龙, 张鹏, 等. 精密喷射成形HM1钢摩擦磨损性能研究[J]. 材料科学与工艺, 2014, 22(5): 108–113.
CHENG Yongqi, WANG Cunlong, ZHANG Peng, et al. Friction and wear properties of HM1 steel processed by precision spray forming[J]. Materials Science and Technology, 2014, 22(5): 108–113. DOI: 10.11951/j.issn.1005-0299.20140519 |
| [6] |
解挺, 杨华平, 杨辉. 摩擦磨损过程的数值模拟研究[J]. 润滑与密封, 2013, 38(12): 88–92.
XIE Ting, YANG Huaping, YANG Hui. Numerical simulation of the process of friction and wear[J]. Lubrication Engineering, 2013, 38(12): 88–92. |
| [7] | 张跃, 谷景华, 尚家香, 等. 计算材料学基础[M]. 北京: 北京航空航天大学出版社, 2007: 100-101. |
| [8] | LUAN Binquan, ROBBINS M O. The breakdown of continuum models for mechanical contacts[J]. Nature, 2005, 435(16): 929–932. |
| [9] | CIEPLAK M, SMITH E D, ROBBINS M O. Molecular origins of friction: The Force on Adsorbed Layers[J]. Science, 1994, 265(5176): 1209–1212. DOI: 10.1126/science.265.5176.1209 |
| [10] | XU Shuai, WAN Qiang, SHA Zhendong, et al. Molecular dynamics simulation of nano-indentation and wear of the γTi-Al alloy[J]. Computational Materials Science, 2015, 110: 247–253. DOI: 10.1016/j.commatsci.2015.08.045 |
| [11] | LI Qunyang, DONG Yalin, PEREZ D, et al. Speed dependence of atomic stick-slip friction in optimally matched experiments and molecular dynamics simulation[J]. Physical Review Letters, 2011, 106(12): 1261011–1261014. |
| [12] | KIM H J, EMGE A, WINTER R E, et al. Nanostructures generated by explosively driven friction: Experiments and molecular dynamics simulations[J]. Acta Materialia, 2009, 57(17): 5270–5282. DOI: 10.1016/j.actamat.2009.07.034 |
| [13] | CHO M H, KIM S J, LIM D S, et al. Atomic scale stick-slip caused by dislocation nucleation and propagation during scratching of a Cu substrate with a nanoindenter: a molecular dynamics simulation[J]. Wear, 2005, 259(7): 1392–1399. |
| [14] | BASKES M I, NELSON J S, WRIGHT A F. Semiempirical modified embedded-atom potentials for silicon and germanium[J]. Physical Review B, 1989, 40(9): 6085–6100. DOI: 10.1103/PhysRevB.40.6085 |
| [15] | STILLINGER F H, WEBER T A. Computer simulation of local order in condensed phases of silicon[J]. Physical Review B, 1985, 31(8): 5262–5271. DOI: 10.1103/PhysRevB.31.5262 |
| [16] | LI Jia, FANG Qihong, ZHANG Liangchi, et al. Subsurface damage mechanism of high speed grinding process in single silicon revealed by atomistic simulations[J]. Applied Surface Science, 2015, 324: 464–474. DOI: 10.1016/j.apsusc.2014.10.149 |
| [17] | BRUKMAN M J, GAO Guangtu, NEMANICH R J, et al. Temperature dependence of single-asperity diamond-diamond friction elucidated using AFM and MD simulations[J]. The Journal of Physical Chemistry C, 2008, 112(25): 9358–9369. DOI: 10.1021/jp711959e |
| [18] | WEN Jialin, MA Tianbao, ZHANG Weiwei, et al. Atomic insight into tribochemical wear mechanism of silicon at the Si/SiO2 interface in aqueous environment: Molecular dynamics simulations using ReaxFF reactive force field[J]. Applied Surface Science, 2016, 390: 216–223. DOI: 10.1016/j.apsusc.2016.08.082 |
| [19] | WYDER U, BARATOFF A, MEYER E, et al. Interpretation of atomic friction experiments based on atomistic simulations[J]. Journal of vacuum science and technology B, 2007, 25(5): 1547–1553. DOI: 10.1116/1.2770743 |
| [20] | BECKERS M, SCHELL N, MARTINS R M S, et al. Microstructure and nonbasal-plane growth of epitaxial Ti2AlN thin films[J]. Journal of Applied Physics, 2006, 99(3): 0349021–0349028. |
| [21] | CUI Bai, SA R, JAYASEELAN D D, et al. Microstructural evolution during high-temperature oxidation of spark plasma sintered Ti2AlN ceramics[J]. Acta Materialia, 2012, 60(3): 1079–1092. DOI: 10.1016/j.actamat.2011.11.010 |
| [22] | JENG Y R, TSAI P C, FANG T H. Molecular dynamics studies of atomic-scale tribological characteristics for different sliding systems[J]. Tribology Letters, 2005, 18(3): 315–330. DOI: 10.1007/s11249-004-2758-3 |
| [23] | KARTHIKEYAN S, AGRAWAL A, RIGNEY D A. Molecular dynamics simulations of sliding in an Fe-Cu tribopair systems[J]. Wear, 2009, 267(5/6/7/8): 1166–1176. |
| [24] | ZHANG Liangchi, TANANKA H. Towards a deeper understanding of wear and friction on the atomic scale: a molecular dynamics analysis[J]. Wear, 1997, 211(1): 44–53. DOI: 10.1016/S0043-1648(97)00073-2 |
| [25] | STONE T W, HORSTEMEYER M F, HAMMI Y, et al. Contact and friction of single crystal nickel nanoparticles using molecular dynamics[J]. Acta Materialia, 2008, 56(14): 3577–35. DOI: 10.1016/j.actamat.2008.03.044 |
| [26] | LUAN Binquan, ROBBINS M O. Contact of single asperities with varying adhesion: Comparing continuum mechanics to atomistic simulations[J]. Physical Review E, 2006, 74: 3577–3584. |
| [27] | GAO Guangtu, CANNARA R J, CARPICK R W, et al. Atomic-scale friction on diamond: a comparison of different sliding directions on (001) and (111) surfaces using MD and AFM[J]. Langmuir, 2007, 23: 5394–5405. DOI: 10.1021/la062254p |
| [28] | MO Yifei, TUENER K T, SZLUFARSKA L. Friction laws at the nanoscale[J]. Nature, 2009, 457: 1116–1119. DOI: 10.1038/nature07748 |
| [29] | LIU Ze, YANG Jiarui, GREY F, et al. Observation of microscale superlubricity in graphite[J]. Physical Review Letters, 2012, 108(20): 2055031–2055035. |
| [30] | ONODERA T, MORITA Y, NAGUMO R, et al. A computational chemistry study on friction of h-MoS2. Part Ⅱ: friction anisotropy[J]. The Journal of Physical Chemistry B, 2010, 114(48): 15832–15838. DOI: 10.1021/jp1064775 |
| [31] | FILLETER T, MCCHESNEY J, BOSTWICK A, et al. Frition and dissipation in epitaxial graphene films[J]. Physical Review Letters, 2009, 102(8): 0861021–0861024. |
| [32] | VAN WIJK M M, DIENWIEBEL M, FRENKEN J W M, et al. Superlubric to stick-slip sliding of incommensurate graphene flakes on graphite[J]. Physical Review B, 2013, 88(23): 2354231–2354236. |
| [33] | HARRISON J A, WHITE C T, COLTON R J, et al. Molecular-dynamics simulations of atomic-scale friction of diamond surfaces[J]. Physical Review B, 1992, 46(15): 9700–9708. DOI: 10.1103/PhysRevB.46.9700 |
| [34] | COOK E H, BUEHLER M J, SPAKOVSZKY Z S. Mechanism of friction in rotating carbon nanotube bearing[J]. Journal of the Mechanics and Physics of Solids, 2013, 61(2): 652–673. DOI: 10.1016/j.jmps.2012.08.004 |
| [35] | SPIJKER P, ANCIAUX G, MOLINARI J F. Relations between roughness, temperature and dry sliding friction at the atomic scale[J]. Tribology International, 2013, 59: 222–229. DOI: 10.1016/j.triboint.2012.02.009 |
| [36] | SØRENSEN M R, JACOBSEN K W, STOLTZE P. Simulations of atomic-scale sliding friction[J]. Physical Review B, 1996, 53(4): 2101–2113. |
| [37] | HU Chengzhi, BAI Minli, LV Jizu, et al. Molecular dynamics investigation of the effect of copper nanoparticle on the solid contact between friction surfaces[J]. Applied Surface Science, 2014, 321: 302–309. DOI: 10.1016/j.apsusc.2014.10.006 |
| [38] | MATSUSHITA K, MATSUKAWA H, SASAKI N. Atomic scale friction between clean graphite surfaces[J]. Solid State Communications, 2005, 136(1): 51–55. DOI: 10.1016/j.ssc.2005.05.052 |
| [39] | ONODERA T, MORITA Y, SUZUKI A, et al. A computational chemistry study on friction of h-MoS2. Part Ⅰ: mechanism of single sheet lubrication[J]. The Journal of Physical Chemistry B, 2009, 113(52): 16526–16536. DOI: 10.1021/jp9069866 |
| [40] | MA Tianbao, HU Yuanzhong, WANG Hui. Molecular dynamics simulation of shear-induced graphitization of amorphous carbon films[J]. Carbon, 2009, 47(8): 1953–1957. DOI: 10.1016/j.carbon.2009.03.040 |
| [41] | LI Qunyang, DONG Yalin, PEREZ D, et al. Speed dependence of atomic stick-slip friction in optimally matched experiments and molecular dynamics simulations[J]. Physical Review Letters, 2011, 106(12): 1261011–1261014. |
| [42] | BALAKRISHNA S G, DE WIJIN A S, BENNEWITZ R. Preferential sliding directions on graphite[J]. Physical Review B, 2014, 89(24): 2454401–2454408. |
 2017, Vol. 25
2017, Vol. 25


