从结构材料的破坏中人们逐渐认识到材料的破坏或断裂现象源自材料的微观尺度或细观尺度,如图 1所示.任何影响金属材料微细观结构变化的因素都会影响材料的宏观力学性能.为了更好地理解飞机用铝合金材料的力学性能,弄清损伤破坏机理,既需要在宏观力学层面上进行研究,又需要在细观力学、甚至微观力学层面上进行研究[1].

|
图 1 结构的损伤源自微观尺度 Figure 1 Damage of structure origin from microstructure scale |
随着人们对材料断裂破坏本质认识的加深,断裂力学适用的局限性也被了解:断裂力学无法描述损伤萌生、演化直至出现宏观裂纹的过程[1-2].前人对铝合金做微观试验分析了大量的研究工作,Liao等[3]研究了微观结构和微观夹杂粒子分布规律.McDowell等[4]研究了疲劳裂纹形成的多晶微观结构的敏感性,为结构在微观方面的的抗疲劳设计和减少裂纹成核部位提供了依据.Li等[5]针对2026铝合金研究得出裂纹成核与与含铁的第二相粒子直接相关.王习术等[6]通过SEM原位观测方法试验研究了铸造镁铝系列合金的微观破坏机理.归纳得到的材料裂纹的萌生主要有以下种形式:夹杂物和基体界面开裂、夹杂物自身断裂、滑移带开裂和晶界开裂等[1, 2-6].杨卫、黄克智等[7-8]在宏微观断裂力学理论和宏微观跨尺度损伤机理进行了大量研究.本文重点研究含有夹杂第二相粒子的2A12铝合金微观结构有限元模型,并考察单个或多个夹杂物对微观应力集中的影响.
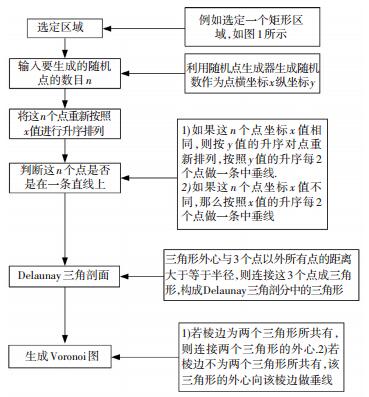
1 铝合金材料微观模拟Voronoi图生成算法如图 2所示[9-10].图 2为算法,图 3为编制MATLAB程序利用100个随机点生成的Voronoi图.
|
图 2 Voronoi图生成算法 Figure 2 Generation algorithm of voronoi diagram |
|
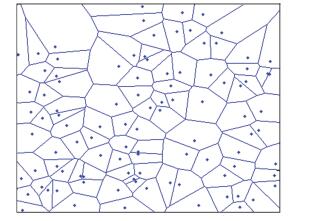
图 3 Voronoi图 Figure 3 Voronoi diagram |
根据统计铝合金材料的晶粒尺寸,得到铝合金晶粒度分布函数,结合Voronoi图,建立铝合金多晶体二维晶粒模型;通过Voronoi算法生成金属材料多晶体显微结构与实际结构的实际微观结构相一致[1].晶粒的取向和相邻晶粒取向之间的差异对短裂纹的萌生有很大影响,Voronoi图只能用来模拟晶核的初始数目和位置,但对于晶粒的取向,则无法模拟.由于晶粒的取向具有很大的随机性.因此,图 3微观组织图中,晶粒的取向是随机产生并确定的[11].
2 材料晶粒间内聚力关系内聚力模型(Cohesive Zone Model,CZM)可以描述界面间的黏着力和摩擦滑移.CZM把晶粒间微裂纹的萌生和扩展以一种显式形式表示,同时符合材料晶粒间力的作用规律.CZM既可反映裂尖前缘(Forward Region)阻碍裂纹起裂的过程,也可描述起裂后弱化区(Wake Region)阻碍裂纹长大的过程.尤其对弹粘塑性材料,应力达到最大值后破坏并不是瞬间发生,利用CZM来反映连续渐进的断裂过程在物理上是合理的[12].
采用双线性内聚力模型,双线性内聚力模型的内聚力-位移关系的方程表达式为[12]
| $ {T_n} = \left\{ \begin{array}{l} \frac{{{\sigma _{\max}}}}{{\delta _n^0}}\delta \;\;\;\;\;\;\;\;\;\;\left( {\delta \le \delta _n^0} \right)\\ {\sigma _{\max}}\frac{{\delta _n^c - \delta }}{{\delta _n^c - \delta _n^0}}\;\;\;\left( {\delta > \delta _n^0} \right) \end{array} \right., $ | (1) |
| $ {T_t} = \left\{ \begin{array}{l} \frac{{{\tau _{\max}}}}{{\delta _t^0}}\delta \;\;\;\;\;\;\;\;\;\;\left( {\delta \le \delta _t^0} \right)\\ {\tau _{\max}}\frac{{\delta _t^c - \delta }}{{\delta _t^c - \delta _t^0}}\;\;\;\left( {\delta > \delta _t^0} \right) \end{array} \right.. $ | (2) |
式中:Tn为法向应力值;Tt为切向应力值;σmax为法向应力最大值;τmax为切向应力最大值;σmax与τmax对应的张开位移值分别为δn0,δt0.在达到最大值时应力开始从最大值减小至零,对应的位移值为δn0,δt0.
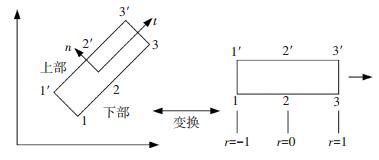
本文所选的是二维六节点内聚单元由两条三结点二次等参线段组成.当受力作用,相邻的单元变形后,界面间有相对位移,并产生内聚力.考虑到法向和切向的不同,引进内聚单元界面的局部坐标系(t, n)[13-14],t为切向,n为法向,δt为切向位移张开量(简称位移量),δn为法向位移张开量,Tt为切向内聚力,Tn为法线内聚力. 图 4所示为六结点内聚线单元模型,节点1,节点2,节点3在内聚力单元的下面,节点1′,节点2′和节点3′在内聚力单元的上面.以上每个节点都具有两个自由度,因此,在整体坐标系(x, y)下,设节点位移向量为
|
图 4 六节点内聚线单元模型 Figure 4 Six node isoparametric of line unite of the CZM |
| $ \boldsymbol{d} = {\left( {{\mu _1},{\nu _1},{\mu _2},{\nu _2},{\mu _3},{\nu _3},{\mu _{1\prime }},{\nu _{1\prime }},{\mu _{2\prime }},{\nu _{2\prime }},{\mu _{3\prime }},{\nu _{3\prime ,}}} \right)^{\rm{T}}}. $ | (3) |
节点1,节点2和节点3的坐标列向量为
| $ {\left( {{X^1},{Y^1},{X^2},{Y^2},{X^3},{Y^3}} \right)^{\rm{T}}}. $ | (4) |
| $ \left\{ \begin{array}{l} {x^上}\\ {y^上} \end{array} \right\} = \left\{ \begin{array}{l} {x^下}\\ {y^下} \end{array} \right\} = \left[ {\begin{array}{*{20}{c}} {{N^1}}&0&{{N^2}}&0&{{N^3}}&0\\ 0&{{N^1}}&0&{{N^2}}&0&{{N^3}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{X^1}}\\ {{Y^1}}\\ {{X^2}}\\ {{Y^2}}\\ {{X^3}}\\ {{Y^3}} \end{array}} \right\}. $ | (5) |
雅可比行列式为
| $ \left| J \right| = \sqrt {{{(\frac{{\partial x}}{{\partial r}})}^2} + {{(\frac{{\partial y}}{{\partial r}})}^2}} . $ | (6) |
式中:
| $ \frac{{\partial x}}{{\partial r}} = \sum\limits_{i = 1}^3 {\frac{{\partial {N^i}}}{{\partial r}}{X^i}} = \left( {r - 0.5} \right){X^1} - 2r{X^2} + {\rm{ }}\left( {r + 0.5} \right){X^3}; $ | (7) |
| $ \frac{{\partial y}}{{\partial r}} = \sum\limits_{i = 1}^3 {\frac{{\partial {N^i}}}{{\partial r}}{Y^i}} = \left( {r - 0.5} \right){Y^1} - 2r{Y^2} + {\rm{ }}\left( {r + 0.5} \right){Y^3}. $ | (8) |
界面单元上表面和下表面的连续位移量为
| $ \boldsymbol{u}=\left\{ {\begin{array}{*{20}{c}} {{\mu^上}}\\ {{\mu^下}}\\ {{v^上}}\\ {{v^下}} \end{array}} \right\}=N \cdot d . $ | (9) |
其中N为形函数,即
| $ N = \left[ {\begin{array}{*{20}{c}} 0&0&0&0&0&0&{{N^1}}&0&{{N^2}}&0&{{N^3}}&0\\ {{N^1}}&0&{{N^2}}&0&{{N^3}}&0&0&0&0&0&0&0\\ 0&0&0&0&0&0&0&{{N^1}}&0&{{N^2}}&0&{{N^3}}\\ 0&{{N^1}}&0&{{N^2}}&0&{{N^3}}&0&0&0&0&0&0 \end{array}} \right] , $ | (10) |
| $ {N^1} = - \frac{1}{2}r\left( {1 - r} \right), $ | (11) |
| $ {N^2} = 1 - {r^2}, $ | (12) |
| $ {N^3} = = \frac{1}{2}r\left( {1 + r} \right). $ | (13) |
界面上表面和下表面的相对位移量为
| $ \Delta \boldsymbol{u}=\boldsymbol{Lu}. $ | (14) |
其中,
| $ \boldsymbol{L} = \left[ {\begin{array}{*{20}{c}} { + 1}&{ - 1}&0&0\\ 0&0&{ + 1}&{ - 1} \end{array}} \right]. $ | (15) |
因此,在有限元中(也称为整体坐标)的坐标系下,有限元中结点位移与内聚力界面的单元连续位移的关系(相对)为
| $ \Delta \boldsymbol{u}=\boldsymbol{LNd}. $ | (16) |
为利用内聚力关系模型,需要得出单元刚度矩阵,界面本构关系在局部坐标上,要把Δu从有限元中的坐标系转到局部坐标系上.如图 4所示坐标系(t, n),切向矢量为
| $ \boldsymbol{V}_t=\left\{ {\begin{array}{*{20}{c}} {\frac{{\partial x}}{{\partial r}}}\\ {\frac{{\partial y}}{{\partial r}}}\\ 0 \end{array}} \right\}. $ | (17) |
法向矢量为
| $ \boldsymbol{V}_n=V_t \times \left\{ {\begin{array}{*{20}{c}} 0\\ 0\\ { - 1} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} { - \frac{{\partial y}}{{\partial r}}}\\ {\frac{{\partial x}}{{\partial r}}}\\ 0 \end{array}} \right\}. $ | (18) |
转换张量为
| $ \boldsymbol{R} = \frac{1}{{\left| J \right|}}\left[ {\begin{array}{*{20}{c}} {\frac{{\partial x}}{{\partial r}}}&{\frac{{\partial y}}{{\partial r}}}\\ { - \frac{{\partial y}}{{\partial r}}}&{\frac{{\partial x}}{{\partial r}}} \end{array}} \right]. $ | (19) |
相对位移向量δ=(δt, δn),决定了内聚力界面上的切向位移量和法向位移量.
| $ \boldsymbol{\delta} = \boldsymbol{RLN}d. $ | (20) |
根据内聚力模型中内聚力—位移关系T(δ),可以求出剪切模量矩阵D,即
| $ \boldsymbol{D}=\frac{\partial \boldsymbol{T}}{\partial \delta}. $ | (21) |
界面的节点力为
| $ f = h\int_{ - 1}^{ + 1} {{\boldsymbol{B}^{\rm{T}}}T\left| J \right|} {\rm{d}}r. $ | (22) |
由虚功原理得到界面刚度矩阵
| $ \boldsymbol{K} = h\int_{ - 1}^{ + 1} {{\boldsymbol{B}^{\rm{T}}}\boldsymbol{DB}\left| {\rm{J}} \right|} d{\rm{r}}, $ | (23) |
式中h为界面单元厚度.
3 有限元模型 3.1 模型的假设在晶粒级尺度上建立模型首先要解决的是晶粒大小的确定.利用内聚力模型和连续介质力学的相关知识做以下假设[14]:
1) 按照Voronoi方法生成2A12铝合金晶粒,参考文献[1]对2A12铝合金微观晶粒尺寸统计分析,本模拟取晶粒尺寸为53 μm[1];
2) 晶粒间的力学关系定义为上节所研究的内聚区模型中的位移-驱动力之间的关系,将基于连续体力学理论的有限单元方法应用到晶粒尺度的力学分析中,从而进行有限元分析;
3) 材料参数不随研究尺度的改变而变化.
3.2 晶粒尺度模型的建立在晶粒级尺度模型中晶粒的形状、大小和方向,根据第1节描述的Voronoi方法,生成含有椭圆形夹杂粒子的Voronoi多边形,认为每个Voronoi多边形是一个连续体,然后,对模型进行网格划分,单元类型和材料特性等参数不变.通过MATLAB编制相关程序获取Voronoi图的几何信息,用MATLAB编写了Voronoi方法的微观结构模拟程序.运用Python脚本语言编写inp文件,导入软件ABAQUS建立铝合金晶粒模型;利用ABAQUS有限元模拟软件的前处理模块CAE建立模型的几何信息部分,并结合MATLAB程序得到2A12铝合金微观模型的ABAQUS输入文件,利用ABAQUS的有限元计算模块STANDARD进行模拟分析计算,最终的可视化结果由ABAQUS的后处理模块分析[15-16].
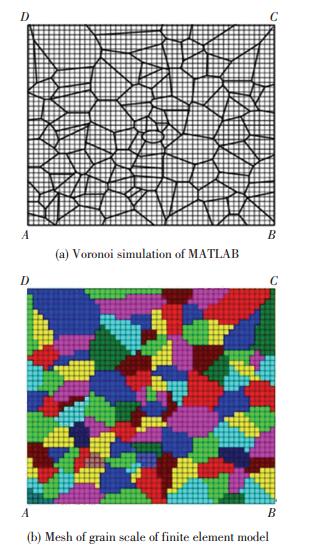
3.3 模型网格划分及边界条件根据上述假设及几何参数和边界条件,模型单元类型为四边形平面应变单元,图 5(b)为划分单元个数为2 304个的晶粒模型,可以看出,网格划分相对晶界较为粗糙.为了满足晶界呈线性,计算时候还需进一步细化网格,但相应的计算时间也会增加,本文计算的微观结构模型共划分的单元个数为36 864个.模拟单向拉伸情况下的应力分布时边界条件为:AB边固定约束,CB、DA保持平直,CD受均匀位移(拉力)作用.
|
图 5 晶粒尺度的有限元模型网格划分 Figure 5 Finite element model for micro grain scale |
用随机数的方法确定晶粒取向来保证2A12铝合金是各相同性材料.在考察夹杂粒子对微观应力集中影响时,假设夹杂粒子的弹性模量为变量,基体弹性模量为常量.考察夹杂粒子与基体脱粘应力时,假设夹杂粒子的弹性模量小于基体.其中,基体的材料参数:弹性模量E、泊松比υ.本文采用的双线性内聚力关系包括3个参数[14]:内聚力在法向和切向为最大值时所对应的法向位移和切向位移δn0和δt0或初始线性模量;内聚力的法向应力和切向应力最大值σmax和τmax;临界张开法向位移和临界张开切向位移δnc和δtc或法向断裂能临界值和切向断裂能临界值φnc=1/2·σmaxδnc,φtc=1/2·τmaxδtc,如表 1和表 2所示.
| 表 1 计算模型材料参数 Table 1 Material parameter of computed model |
| 表 2 计算模型晶界参数 Table 2 Grain boundaries parameter of computed model |
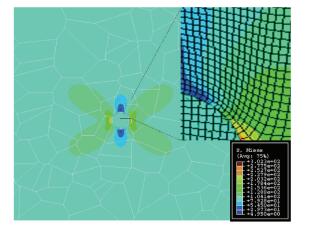
由于要考虑夹杂粒子的不同弹性模量,此处基体材料按照表 1参数选择,粒子的弹性模型按照基体的倍数变化.在满足模型拉伸不破坏的情况下,并结合实际铝合金微观结构分析特点,大部分裂纹在Al7Cu2Fe和Mg2Si夹杂粒子处产生,且这些粒子通常近似圆形,第二相夹杂粒子尺寸大小一般为15~40 μm.其中,Mg2Si夹杂粒子比基体软,通常为脱粘裂纹,其弹性模型小于基体.选择远场拉应力为100 MPa,粒子的平面形状为圆形.考虑夹杂粒子所处位置,在Voronoi图程序进行算法优化,使得生成圆形粒子附近较小的晶粒和相邻的较大晶粒相合,保证粒子所处的位置在多晶粒晶界处,符合实际微观组织粒子的多数位置,且粒子半径取25 μm.应力云图与局部网格如图 6所示.
|
图 6 单个夹杂粒子应力云图与局部网格划分 Figure 6 Stress distribution and local detailed mesh for single particles |
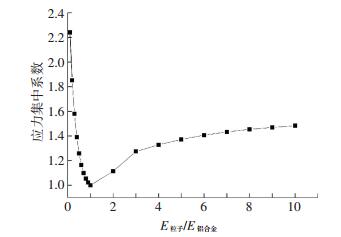
图 7为夹杂粒子的弹性模量和铝合金的弹性模量比值与应力集中系数之间的关系,其中,E粒子表示夹杂粒子的弹性模量,E铝合金表示铝合金基体的弹性模量.在小于基体弹性模量时,随着夹杂粒子弹性模量的增加应力集中系数减小;在大于基体弹性模量时,随着夹杂粒子弹性模量的增加应力集中系数减增加.应力集中系数定义为
|
图 7 夹杂粒子的不同弹性模量和应力集中系数之间的关系 Figure 7 Relationship of stress concentration factor and different elastic modular |
| $ {K_t} = \frac{{{S_{\max }}}}{{{S_{0\max }}}}. $ |
式中:S0 max=100 MPa;Smax为不同弹性模量的夹杂粒子时的最大正应力.
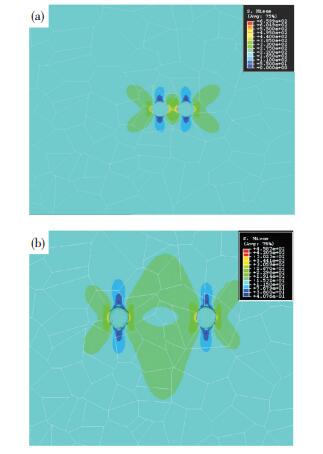
4.2 两个夹杂物对微观应力集中的影响夹杂粒子的大小、数量及分布状态(夹杂粒子的相对位置)影响结构内部应力集中.本节主要是针对两个夹杂粒子间的大小和相对位置进行计算.在建模时夹杂粒子半径取r1=25 μm,与之相对应的另外一个粒子的半径尺寸分别取r2=25 μm和r2=20 μm,两粒子中心的距离为d.粒子和基体材料参数选择按表 1进行设置.计算时取粒子位置的两种极端情况:两粒子排列方向与加载方向垂直和排列方向与加载方向一致.其他两粒子成一定角度的情况介于两者之间.图 8为夹杂粒子排列方向与加载方向垂直时,两粒子距离不同时的有限元应力云图.
|
图 8 夹杂粒子排列方向与加载方向垂直时的有限元应力云图 Figure 8 Finite element stress distribution for double particles when particles plumb the load:(a) distance of particle center being 75 μm; (b) distance of particle center being 150 μm |
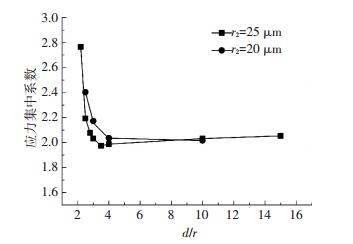
计算可知,当两个夹杂粒子之间的距离较小时,最大应力点出现在两个夹杂粒子相近的位置上.当仅存在一个半径为25 μm的夹杂第二相粒子时,Kt=2.065.通过对图 9和图 10的分析可知,当两个夹杂第二相粒子方向与加载方向相同时,相对于第二相粒子的情况,第一个粒子处的应力集中能够得到缓和,随着d/r比值的增加,趋于平稳.当两个夹杂粒子排列方向与加载方向垂直时,相对于单个夹杂粒子的情况,两个夹杂粒子的应力集中会增加,特别当d/r比值接近2时(因为不考虑夹杂粒子相互接触联合的情况,故所选的d/r比值均大于2),应力集中系数明显增加.随着d/r比值的增加,这种加强作用趋于平稳,当d/r比值处在6左右时,应力集中系数基本恢复到单夹杂粒子时的大小.
|
图 9 夹杂粒子排列方向与加载方向垂直时的应力集中系数 Figure 9 Stress concentration factor when particle plumb the load |
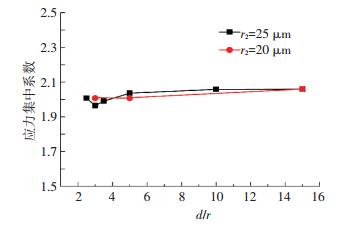
|
图 10 夹杂粒子排列方向与加载方向相同时的应力集中系数 Figure 10 Stress concentration factor when particle along the load |
基于Voronoi图方法较好地模拟了含有夹杂物(第二相粒子)2A12铝合金的微观组织结构.运用内聚力模型中的内聚应力-位移关系描述晶粒之间、晶粒与夹杂粒子之间的力学关系,实现了2A12铝合金的微观结构有限元分析.通过对微观结构的有限元模型分析得出夹杂粒子的形状、数量及分布状态对结构微观应力集中的影响.
| [1] |
卞贵学, 陈跃良, 张勇, 等. 2A12铝合金疲劳裂纹成核与扩展机理[J]. 材料研究学报, 2012, 26(5): 521–526.
BIAN Guixue, CHEN Yueliang, ZHANG Yong, et al. Microstructural mechanism fatigue crack nucleation and propagation of 2A12 aluminum alloy[J]. Chinese Journal of Materials Research, 2012, 26(5): 521–526. |
| [2] |
刘大海, 谢永鑫, 黎俊初. 工艺参数工艺参数对7075铝合金板材时效成形性的影响[J]. 材料科学与工艺, 2015, 23(3): 50–56.
LIU dahai, XIE yongxin, LI junchu. Influence of process parameters creep age forming formability of 7075aluminum alloy sheet[J]. Materials Science and Technology, 2015, 23(3): 50–56. DOI: 10.11951/j.issn.1005-0299.20150310 |
| [3] | LIAO Min. Probabilistic modeling of fatigue related microstructural parameters in aluminum alloys[J]. Engineering Failure Mechanics, 2009, 76: 668–680. DOI: 10.1520/JAI101558 |
| [4] | MCDOWELL D L, DUNNE F P E. Microstructure-sensitive computational modeling of fatigue crack formation[J]. International Journal of Fatigue, 2010, 32(9): 1521–1542. DOI: 10.1016/j.ijfatigue.2010.01.003 |
| [5] | LI J X, ZHAI T, GARRATT MD, et al. Four-point-bend fatigue of AA2026 aluminum alloys[J]. Metallurgical and Materials Transactions A, 2005, 36: 2529–2549. DOI: 10.1007/s11661-005-0126-z |
| [6] |
王习术, 汤彬, 陶沙. 铸造镁铝合金的微观破坏机理原位观测技术与应用[J]. 机械工程材料, 2006, 30(2): 1–5.
WANG Xishu, TANG Bin, TAO Sha. In-site observation technology and application of fatigue crack initiation and propagation for cast magnesium alloys[J]. Materials for Mechanical Engineer, 2006, 30(2): 1–5. |
| [7] |
杨卫. 宏微观断裂力学[M]. 北京: 国防工业出版社, 1995: 1-13.
YANG Wei. Macro and Micro Fracture Mechanics[M]. Beijing: National Defense Industry Press, 1995: 1-13. |
| [8] |
黄克智, 王自强. 材料的宏微观力学与强韧化设计[M]. 北京: 清华大学出版社, 2003: 12-23.
HUANG Kezhi, WANG Ziqiang. Micro-mechanics and strengthening and toughening design of materials[M]. Beijing: Tsinghua University Press, 2003: 12-23. |
| [9] |
傅廷亮, 尹雪涛, 张扬. Voronoi算法模型及其程序实现[J]. 计算机仿真, 2006, 23(10): 89–91.
FU Tingliang, YIN Xuetao, ZHANG Yang. Voronoi algorithm model and the realization of Tts program[J]. Computer Simulation, 2006, 23(10): 89–91. DOI: 10.3969/j.issn.1006-9348.2006.10.023 |
| [10] |
司良英, 邓关宇, 吕程. 基于Voronoi图的晶体塑性有限元多晶几何建模[J]. 材料与冶金学报, 2009, 8(3): 193–195.
SI liangying, DENG Guanyu, LU Cheng. Polycrystal geometry modeling of crystal plasticity finite element method with voronoi diagram[J]. Journal of Materials and Metallurgy, 2009, 8(3): 193–195. DOI: 10.14186/j.cnki.1671-6620.2009.03.001 |
| [11] |
张超. 晶体塑性成形的数值模拟[D]. 济南: 山东大学, 2005: 43-50. ZHANG Chao. The Numerical Simulation of Crystal Plastic Deformation[D]. Ji′nan:Shandong University, 2005:43-45. http: //cdmd. cnki. com. cn/Article/CDMD-10422-2005132293. htm |
| [12] |
张军. 界面应力及内聚力模型在界面力学的应用[M]. 郑州: 郑州大学出版社, 2011: 1-16.
ZHANG Jun. Interface stress and cohesion model in the interface mechanics[M]. Zhengzhou: Zhengzhou University Press, 2011: 1-16. |
| [13] | PHILLIPS D R, IESULAURO E, GLAESSGEN E H.Multiscale modeling of metallic materials containing embedded particles[C]//45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Confer. April 2004. California :Palm Springs, 2004:19-22. http://arc.aiaa.org/doi/abs/10.2514/6.2004-1699 |
| [14] | BJERKE T W, LAMBROS J. Theoretical development and experimental validation of a theramally dissipative cohesive zone model for dynamic fracture of amorphous polymers[J]. Jouranl of the Mechanics and Physics of Solids, 2003, 51(6): 1147–1170. DOI: 10.1016/S0022-5096(02)00145-X |
| [15] |
吴艳青, 张克实. 利用内聚力模型(CZM)模拟弹粘塑性多晶体的裂纹扩展[J]. 应用数学和力学, 2006, 27(4): 454–454.
WU Yanqing, ZHANG Keshi. Crack propagation in polycrystalline elastic-viscoplastic materials using cohesive zone models[J]. Applied Mathematics and Mechanics, 2006, 27(4): 454–454. |
| [16] |
黄刘刚. 内聚力模型的分析及有限元子程序开发[D]. 郑州: 郑州大学, 2010: 28-39. HUANG Liugang.The analysis of cohesive zone model and user-defined subroutine development in finite element method[D].Zhengzhou : Zhengzhou Uiversity:2010:28-29. http: //cdmd. cnki. com. cn/Article/CDMD-10459-2011012597. htm |
 2017, Vol. 25
2017, Vol. 25


