碳化硅材料拥有禁带宽度大、热导率高、击穿电场强度高、介电常数低和抗辐射能力强等特性,广泛应用于MEMS、高能半导体器件等领域[1].碳化硅硬度高,加工困难,目前唯一能实现全局平坦化的化学机械抛光(CMP)技术是加工碳化硅的主要手段[2].
化学机械抛光的切削深度为纳米级或亚纳米级,由于尺寸效应,传统的切削理论无法很好地解释CMP过程中材料表面形成和去除机理.分子动力学(MD)仿真技术[3]具有超高的时间空间分辨率,是探究原子尺度过程和微观机理的理想研究方法,目前MD仿真广泛应用于纳米力学[4]、摩擦学[5]和精加工等领域[6-13].
Si等[6]采用分子动力学研究了晶体硅CMP过程中原子层的机械去除机理,指出刻划深度对加工表面有直接影响:刻划深度0.1 nm时,可实现Si表面的单原子层去除,获得无变质层的有序晶面;而1.0 nm切深的刻划表面粗糙,产生不定型结构层.Li等[7]应用分子动力学研究了刀尖形状、切深、刀具速度、刻划方向等因素对不同表面粗糙度单晶铜的纳米级刻划的影响规律和材料去除机理.尽管许多学者采用分子动力学对铜、硅等材料的CMP过程进行了仿真研究[8-11],对碳化硅材精密加工的MD仿真才刚开始.Goel等[12]采用分子动力学研究了立方碳化硅纳米切削时原子层面的韧性响应,模拟结果显示碳化硅经历了SP3到SP2的结构转变,导致碳化硅亚表层的石墨化.他们采用该方法进一步定量分析了立方碳化硅切削时金刚石刀具的磨损[13].
本文采用分子动力学软件LAMMPS探究立方碳化硅CMP过程中金刚石磨粒对碳化硅和表面氧化膜的机械刻划行为,对比分析碳化硅CMP过程中机械作用参数对碳化硅和氧化膜的结构、摩擦力和原子去除率的影响规律.
1 CMP仿真模型建立一般可以认为,在CMP过程中嵌入抛光垫的磨粒对工件的刻划作用是材料去除的主要原因,因此建立碳化硅CMP过程的MD模型如图 1所示.
|
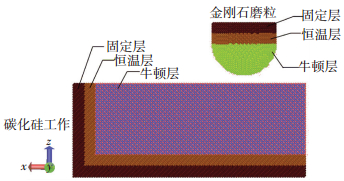
图 1 碳化硅CMP过程分子动力学模型 Figure 1 Molecular dynamics model of silicon carbide in the process of CMP |
综合考虑计算量与仿真精度,建立工件模型尺寸为21.6 nm×12.9 nm×8.6 nm,共有240 000个原子,金刚石磨粒模型下端为半球体,半径为3.0 nm,模拟嵌入抛光垫磨粒的露出部分,上半部分为圆柱体,高度2.0 nm,磨粒模型共有19 348个原子.工件和磨粒模型均划分为3层:固定层、恒温层和牛顿层, 恒温层温度设定为300 K.考虑到碳化硅与金刚石硬度接近,故金刚石磨粒未设置为刚体,可以观察到磨粒形貌变化.仿真盒子y方向采用周期性边界条件,其余方向皆采用自由边界.磨粒压入深度为1.5 nm,刻划方向为x正方向,刻划速度为100 m/s,模拟系综为NVE.
原子间势函数的选择影响着仿真结果的精度,本文仿真采用适合用于共价晶体的Tersoff势函数[14],该势函数可以较好地描述C-C、Si-Si、C-Si原子作用关系.
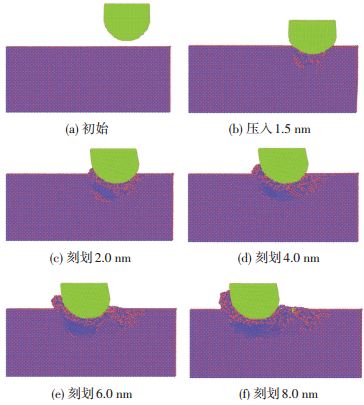
2 刻划过程现象分析选取时间步长为1 fs,以金刚石磨粒对碳化硅工件进行刻划仿真,仿真分为压入和刻划两个过程,压入深度为1.5 nm,刻划距离为8.0 nm,磨粒压入和刻划过程如图 2所示.由图 2可观察到:随着磨粒的压入,金刚石磨粒出现一定程度的变形,磨粒沿x方向的运动推动工件牛顿层原子向前挤压,破坏碳化硅工件表面,产生沟壑;碳原子和硅原子在磨粒前段的堆积效应形成切屑,从而起到材料去除的作用.
|
图 2 磨粒压入及刻划现象过程 Figure 2 The process of abrasive pressing in and scratching the workpiece:(a)initial stage; (b)pressing 1.5 nm; (c)scratching 2.0 nm; (d)scratching 4.0 nm; (e)scratching 6.0 nm; (f) scratching 8.0 nm |
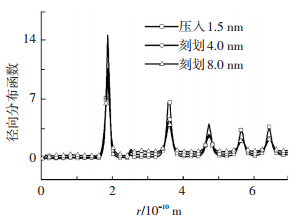
径向分布函数是分子动力学中常见的用于分析结构的物理参数,通过固体中原子排列的有序程度来描述固体的结构,通过峰的位置、形状、周期性来判断晶体,非晶体的结构变化.由于测得切削碳化硅时亚表层受影响的深度为2.6 nm,提取对应磨粒压入时刻、刻划4.0 nm和8.0 nm时刻碳化硅在该特征层的径向分布函数进行对比.
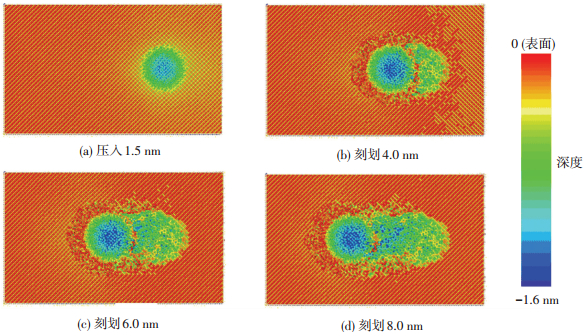
由图 3可知,随着加工的进行,径向分布函数的峰值变小,曲线变宽,说明第一近邻位置处的原子密度减小,刻划后的晶体内部结构发生了变化,逐渐产生非晶相变.而由隐去磨粒,对不同高度的原子层进行着色的图 4可以看出,磨粒的刻划使工件表面产生了沟壑,磨粒顶端部分的刻划深度最大,然而随着刻划的进行,磨粒经过的位置的深度小于磨粒接触位置的深度,这说明了对于碳化硅这样硬度极大的脆性材料,从原子层面上依旧可以观测到其弹性变形.
|
图 3 切削层不同刻划距离径向分布函数 Figure 3 RDF at different distance of the cutting layer |
|
图 4 碳化硅工件压入及刻划后形貌 Figure 4 Morphology of silicon carbide after pressing and scratching for some distance:(a) pressing 1.5 nm; (b) scratching 4.0 nm; (c) scratching 6.0 nm; (d) scratching 8.0 nm |
本文针对不同刻划参数进行仿真,模拟了磨粒沿z轴下降压入工件并沿x轴方向移动刻划工件的过程.在本仿真中,每隔100时间步输出一次信息,0~18 000时间步为磨粒下压但尚未接触工件的过程,18 000~48 000时间步为磨粒压入工件的过程,48 000~128 000时间步为磨粒刻划过程.提取出温度、切削力和原子去除率作为宏观输出量进行分析,其中温度为模型中牛顿层的温度.
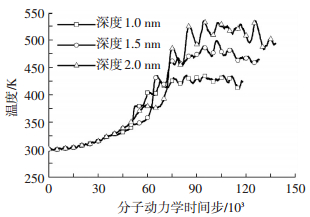
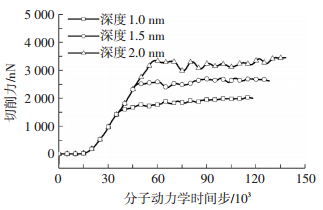
3.1 刻划深度对宏观量的影响调整压入深度分别为1.0、1.5、2.0 nm,磨粒半径均为3.0 nm,刻划速度均为100 m/s,其温度和切削力变化分别如图 5、6所示.分析可知,刻划深度越大,磨粒与工件之间相互挤压、剪切及摩擦的原子越多,原子热振动频率越大,温度也就更高;同时刻划深度越大,磨粒所受阻力也越多,切削力也越大,在本仿真中切削力为千nN级别.对脱离工件上表面的原子数量进行统计,即刻划结束后z坐标高于模型高度8.6 nm的原子,从而分析材料去除效果,其统计如表 1所示,可知,刻划深度越大,原子去除率越高,且变化非常明显.
|
图 5 刻划深度对温度的影响 Figure 5 Effect of scratching depth on temperature |
|
图 6 刻划深度对切削力的影响 Figure 6 Effect of scratching depth on cutting force |
| 表 1 刻划深度对原子去除个数的影响 Table 1 The effect of scratching depth on the number of atoms removed |
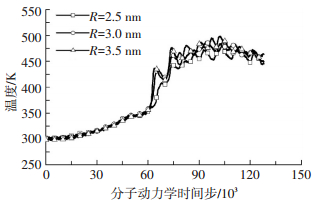
建立3种磨粒模型,半径分别为2.5、3.0、3.5 nm,刻划深度为1.5 nm,刻划速度为100 m/s,其温度和切削力变化曲线如图 7、8所示.刻划温度受磨粒半径的影响不大;但随着磨粒切削半径的增大,磨粒与工件的接触面积增大,切削力随之增大.
|
图 7 磨粒大小对温度的影响 Figure 7 Effect of the abrasive size on temperature |

|
图 8 磨粒大小对切削力的影响 Figure 8 Effect of the abrasive size on cutting force |
由表 2显示的原子去除数可知,在刻划深度相同的情况下,去除原子数与磨粒半径并非线性关系,磨粒大小的改变对材料去除影响非常有限.说明磨粒半径增大后虽然沟壑会有所增宽,但未必会使脱离表面的原子数变多,有可能使原子向两侧压紧.
| 表 2 磨粒大小对原子去除个数的影响 Table 2 The effect of the abrasive size on the number of atoms removed |
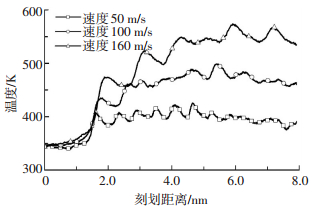
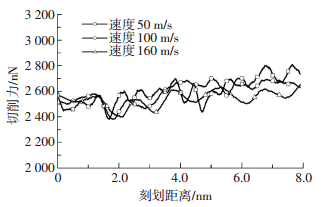
由于分子动力学中基本时间单位为ps,为了能够准确地获得原子的相关运动状态,分子动力学步必须取得很小,如果仿真过程的磨粒速度过小,则计算量会非常大,影响仿真效率.故选取刻划速度为50、100、160 m/s进行对比,其余参数选取刻划深度1.5 nm,磨粒半径3.0 nm,仅提取刻划过程,温度变化和切削力变化如图 9、10所示.
|
图 9 刻划速度对温度的影响 Figure 9 Effect of scratching speed on temperature |
|
图 10 刻划速度对切削力的影响 Figure 10 Effect of scratching speed on cutting force |
由图 9和10可以看出,刻划速度的改变对切削力几乎没有影响,而刻划速度越小,工件温度就拥有更多的时间将温度传递给恒温层,故温度越低.由表 3可知,刻划速度的提高也会提高原子去除数量,但影响不是很大,其原理是快速运动的磨粒会使脱离基体的碳化硅原子运动更远,从而减少弹性恢复所需的距离和时间.
| 表 3 刻划速度对原子去除个数的影响 Table 3 The effect of scratching speed on the number of atoms removed |
在碳化硅化学机械抛光(CMP)过程中,化学反应起着重要的作用.由于抛光液一般具有一定的腐蚀作用,在摩擦热和抛光液的共同作用下,碳化硅表面会氧化形成一层无定型二氧化硅.为对比分析,有必要对碳化硅表面生成的无定型二氧化硅的机械刻划作用进行仿真研究.
建立了底层为立方碳化硅,上层铺设有氧化膜的工件模型.氧化膜模型尺寸为21.4 nm×12.8 nm×2.1 nm,碳化硅底层尺寸为21.6 nm×12.9 nm×6.4 nm.金刚石磨粒模型与前文一致,下半部分为半径3.0 nm的半球体,上部分为高度2.0 nm的圆柱体,磨粒模型放置在氧化膜上方0.9 nm处,将工件模型和磨粒模型也分别分为固定层、恒温层、牛顿层,无定型二氧化硅层依旧采用tersoff势函数描述,其中碳氧之间的相互作用关系用LJ势来描述,其刻划形貌图如图 11所示.

|
图 11 无定型二氧化硅氧化膜刻划形貌 Figure 11 Morphology of the amorphous silicon dioxide film during the process of scratching:(a)pressing 1.5 nm; (b)scratching 8.0 nm |
由图 11可知,磨粒在刻划过程中形变非常小,这是因为无定型二氧化硅原子间空隙较大、结构蓬松,键合力弱.当磨粒挤压工件原子时,工件中碳原子与硅原子、碳原子与氧原子间的作用力要大于硅原子与氧原子间的作用力,排斥力使硅氧原子变得更加紧密,故磨粒变形较小.观察发现,因为氧化膜的多空结构,氧化硅刻划过程中没有切屑产生.磨粒压入和刻划过程中,磨粒接触域的氧化硅下方及前侧方受到挤压,使氧化膜致密化,硅氧原子不在磨粒前端堆积;刻划后的表面相对平整,无弹性回复和剥落,故无磨屑产生.作为底层的碳化硅基底原子之间作用力较大,在磨粒下压及刻划过程中没有发生明显形变.
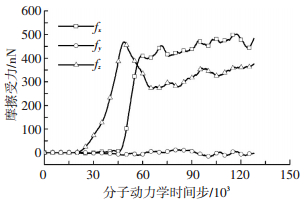
图 12给出了刻划氧化膜过程中磨粒在x、y、z 3个方向的受力变化曲线,由图可知,与刻划碳化硅时不同,在刻划氧化膜的过程中,最终磨粒的z方向受力要小于x方向受力,这是由氧化膜的疏松结构使被压紧原子的弹性恢复变少导致的.相比于碳化硅刻划(见图 6),刻划氧化膜时磨粒受力仅为其1/5左右,即,氧化膜的生成可以大幅度降低切削力.这是由于碳化硅和氧化硅的键合能大不相同,同时也因磨粒与氧化层接触及刻划时仅使氧化层塑性变形、塑性致密化所需的排斥力大大小于破坏晶格的排斥力.
|
图 12 氧化膜刻划磨粒受力曲线 Figure 12 Abrasive forces during scratching of the oxide film |
1) 在刻划过程中碳化硅表面结构会被破坏,并逐渐出现非晶化现象,在原子层面上碳化硅材料在加工过程中会呈现出明显的弹性恢复.
2) 刻划深度、刻划速度和磨粒尺寸增大都会使刻划过程的工件温度升高;刻划深度和磨粒尺寸增大会使刻划力增大,而刻划速度的改变对切削力几乎没有影响;刻划深度对材料去除率影响最大,磨粒压入越深去除原子越多;在保证冷却的情况下提高抛光速度也有利于材料去除;在刻划深度相同的情况下,磨粒尺寸对材料去除率的影响有限.
3) 在抛光过程中生成的无定型二氧化硅氧化膜会大幅度降低磨粒受力,但在氧化膜刻划过程中,氧化膜倾向于致密化,故而无磨屑产生.
| [1] |
肖强, 李言, 李淑娟. SiC单晶片CMP超精密加工技术现状与趋势[J]. 宇航材料工艺, 2010, 40(1): 9–13.
XIAO Qiang, LI Yan, LI Shujuan. Situation and development trends of CMP for SiC monocrystal wafer[J]. Astronautics Materials Technology, 2010, 40(1): 9–13. |
| [2] |
雷红, 雒建斌, 马俊杰. 化学机械抛光(CMP)技术的发展、应用及存在问题[J]. 润滑与密封, 2002(4): 73–76.
LEI Hong, LUO Jianbin, MA Junjie. Development, application and problems on chemical mechanical polishing (CMP) technology[J]. Lubrication and Seals, 2002(4): 73–76. |
| [3] | ALDER B J, WAINWRIGHT T E. Phase transition for a hard sphere system[J]. Journal of Chemical Physics, 1957, 27(5): 1208–1209. DOI: 10.1063/1.1743957 |
| [4] |
袁林, 敬鹏, 刘艳华, 等. 多晶银纳米线拉伸变形的分子动力学模拟研究[J]. 物理学报, 2014, 63(1): 268–273.
YUAN Lin, JING Peng, LIU Yanhua, et al. Molecular dynamics simulation of polycrystal silver nanowires under tensile deformation[J]. Physics Bulletin, 2014, 63(1): 268–273. DOI: 10.7498/aps.63.016201 |
| [5] | HAN Xuesong, GAN Y X. Analysis the microscopic solid-based wear process in the chemical mechanical planarization[J]. Surface & Interface Analysis, 2011, 44(5): 590–600. |
| [6] | SI L, GUO D, LUO J, et al. Monoatomic layer removal mechanism in chemical mechanical polishing process: a molecular dynamics study[J]. Journal of Applied Physics, 2010, 107(6): 064310–064310. DOI: 10.1063/1.3327448 |
| [7] | LI Jia, FANG Qihong, LIU Youwen, et al. Scratching of copper with rough surfaces conducted by diamond tip simulated using molecular dynamics[J]. International Journal of Advanced Manufacturing Technology, 2015, 77(5/6/7/8): 1057–1070. |
| [8] | MIYOSHI A, NAKAGAWA H, MATSUKAWA K. Simulation on Chemical Mechanical Polishing Using Atomic Force Microscope[M]. Berlin: Springer-Verlag, 2005. |
| [9] | PEI Q X. Large scale molecular dynamics study of nanometric machining of copper[J]. Computational Materials Science, 2007, 41(2): 177–185. DOI: 10.1016/j.commatsci.2007.04.008 |
| [10] | LI J, FANG Q, ZHANG L, et al. The effect of rough surface on nanoscale high speed grinding by a molecular dynamics simulation[J]. Computational Materials Science, 2015, 98: 252–262. DOI: 10.1016/j.commatsci.2014.10.069 |
| [11] | GOEL S, LUO X, AGRAWAL A, et al. Diamond machining of silicon: a review of advances in molecular dynamics simulation[J]. International Journal of Machine Tools & Manufacture, 2015, 88: 131–164. |
| [12] | GOEL S, LUO X, REUBEN R L, et al. Atomistic aspects of ductile responses of cubic silicon carbide during nanometric cutting[J]. Nanoscale Research Letters, 2011, 6(1): 589–597. DOI: 10.1186/1556-276X-6-589 |
| [13] | GOEL S, LUO X, REUBEN R L. Molecular dynamics simulation model for the quantitative assessment of tool wear during single point diamond turning of cubic silicon carbide[J]. Computational Materials Science, 2011, 51: 402–408. |
| [14] | TERSOFF J. New empirical approach for the structure and energy of covalent systems[J]. Phys Rev, 1988, B37: 6991–7000. DOI: 10.1103/PhysRevB.37.6991 |
 2018, Vol. 26
2018, Vol. 26


