等径弯曲通道变形(equal channel angular pressing,简称ECAP)是一种通过变形加工改善金属材料微观结构,有利于提升机械性能的独特加工方法,也是目前最具工业化应用前景的技术之一.ECAP可以在金属材料中实现从亚微米到纳米尺寸的大晶粒细化[1],主要集中在制备方法与常规温度下的组织性能研究[2-3].现有研究表明[4],ECAP除了晶粒细化改善材料性能之外,回复和再结晶过程还为后续的微观结构演变提供了驱动力,这通常会产生较高的储存能和较低的再结晶温度.细晶粒材料比粗晶材料更快地再结晶,因为晶界是有利的成核位置.而过多的储存能会使材料产生过高的内应变和高能非平衡的晶界,使超细晶材料在热力学上处于不稳定状态,在适当条件下具有向亚稳状态和平衡状态转变的趋势[5-6].ECAP退火后的超细晶铜含有高密度位错的大角度晶界,晶粒异常生长且出现不连续的再结晶现象[7-8],并且其中一些在特定温度下容易发生再结晶[9].
文献[10]研究了纯铜ECAP挤压,在8道次变形后抗拉强度达到410 MPa,延伸率不足15%;12道次变形后强度略有下降,延伸率却有明显提升,变形储存能释放,位错密度降低.对ECAP加工的铜的热稳定性研究表明[11-13],再结晶比传统轧制粗晶铜更快,ECAP后的储存能更大,激活能比观察到的冷轧铜更低.超细晶铜的热稳定性差是由于大角度边界的增多导致成核条件增强.有学者认为[14-15],激活能随着温度升高而增大,当激活能接近或高于材料扩散能时,超细晶材料便会发生再结晶和晶粒长大,这种激活能的增加与退火过程中晶界结构的恢复有关.从工业应用的角度来看,对严重变形材料的热稳定性,即它们对显微组织恢复过程(回复和再结晶)抵抗性的研究是评估它们适用性的必要步骤.
本文以工业纯铜为研究对象,对其ECAP后的组织及后续退火过程中的再结晶行为进行研究.
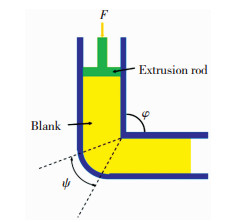
1 实验实验所用材料为退火态的工业纯铜(T1)板材,使用传统的ECAP方法,在等径转角挤压过程中采用C路径在室温下对其进行12道次ECAP变形实验.将14.5mm(长)×14.5mm(宽)×90mm(高)的坯料从挤压棒中加工出来,如图 1,两通道之间的角度ϕ为90°,交叉点处的曲率外弧角Ψ为20°,挤压速度2 mm/s.ECAP变形后,在100~300 ℃之间对选定的样品进行等温退火,其中样品在每个温度下保持10 min.
|
图 1 等径角挤压原理图 Fig.1 Schematic of ECAP extrusion |
在JEM200CX透射电子显微镜上进行微观组织分析,试样双喷减薄,减薄液体积分数为33%硝酸甲醇溶液,进行选区衍射拍照.光学显微组织观察,对光学试样进行抛光,抛光后的试样再进行化学浸蚀,浸蚀剂为5 g FeCl3+10 mL盐酸+100 mL水.经过抛光、浸蚀后在光学显微镜(OLYMPUS金相显微镜)下进行光学金相分析.
采用数显显微维氏硬度计(401-MVD)对原始样及变形试样面进行显微硬度测试,加载载荷为2 N,加载时间为15 s.根据Arrhenius公式进行再结晶激活能的计算.
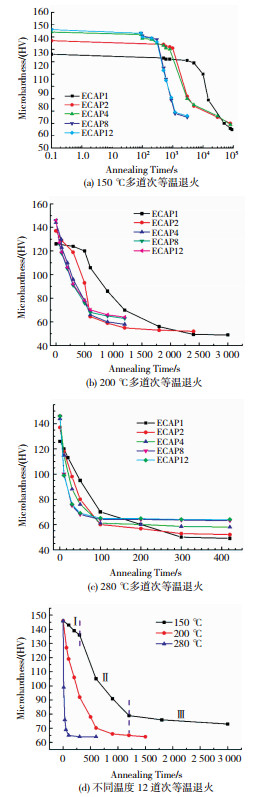
2 结果 2.1 退火后硬度变化如图 2,在3个温度(150、200、280 ℃)下对不同变形道次的坯料进行退火实验.对比不同道次超细晶Cu软化曲线可以发现:在不同温度下进行等温退火时,随着变形道次的增加,软化速度越快,完成软化所需的时间就越短;150 ℃时1道次变形后的超细晶铜的软化速度很慢,72 000 s以后才基本达到稳态;而12道次变形后的超细晶铜的软化速度很快,1 800 s后就趋于稳态.对比前3幅图可发现:随着退火时间的增加,硬度明显降低;各道次在不同温度下达到稳态后的硬度随变形道次的增大而增大,其中200和280 ℃时较为明显,而150 ℃时只有细微变化;随着退火温度的提高,各组试样再结晶完成所需时间变短,即再结晶速率增大.由图 2(d)可知,等温退火过程中各组试样的硬度变化趋势相同,其硬度变化可分为3个阶段:第1阶段硬度变化不大,略有下降,此阶段为回复阶段;第2阶段硬度急剧下降,超细晶开始发生再结晶;第3阶段硬度逐渐趋于稳定,再结晶完成.
|
图 2 各道次等温退火时室温硬度随时间的变化曲线 Fig.2 Curves of room temperature hardness with time after isothermal annealing of each pass:(a)isothermal annealing at 150 ℃; (b)isothermal annealing at 200 ℃; (c)isothermal annealing at 280 ℃; (d)12 passes isothermal annealing at different temperature |
温度变化对ECAP变形后的超细晶Cu软化性能影响较大,退火温度越高,发生再结晶时间越短.12道次超细晶铜150 ℃等温退火时,开始再结晶的时间为300 s,完成再结晶时间大约为1 200 s,此时材料的硬度为79 HV;当退火温度上升至200 ℃时,开始再结晶所需时间为100 s,完成再结晶时间缩短至600 s,材料硬度为70 HV,而280 ℃时再结晶仅需50 s.
2.2 退火后组织变化对图 2中3个温度下ECAP12道次超细晶Cu完成再结晶的时间进行对比,150 ℃时的时间相对更长一些,此时微观组织的变化比较显著,因此,本文观察了12道次ECAP超细晶纯Cu在150 ℃不同退火时间条件下的组织(图 3).

|
图 3 12道次ECAP超细晶纯Cu在150 ℃经不同时间等温退火后金相组织 Fig.3 Microstructure of 12-pass ECAP ultra-fine grained pure copper after isothermal annealing at 150 ℃ for different time |
由图 3可以看出:经过220 s退火后,一小部分能量较高的小晶粒开始再结晶,而大部分区域组织变化不明显,仍保持ECAP变形后的切变带组织,由于时间较短,从整个过程来看是以回复过程为主,通过点缺陷的消失和位错重排而实现,同时与此相应的储存能被释放,此时的硬度有所下降(图 2(d));随着保温时间的延长,发生再结晶的晶粒越来越多,500 s退火时,部分区域细小的多边形再结晶粒沿着晶界边缘已经形成,而且还没有长大,还有一部分区域,此时仍为变形组织,ECAP变形的带状仍然可见,晶粒表现为已再结晶晶粒和未再结晶晶粒混合的双峰结构,此时位错发生攀移,再结晶区域增加,位错密度降低,硬度明显下降;当延时到800 s时,从微观结构可以看出,再结晶已基本完成,再结晶晶粒分布还不均匀,从图 2(d)硬度变化图看,此时其硬度变化还没进入稳态,再结晶还在继续;退火时间1 000 s后,其硬度变化不大,已进入一个稳态,说明12道次ECAP超细晶Cu在150 ℃时完成再结晶的时间大约需要1 000 s,当再结晶完成后,随时间延长,晶粒并没有明显长大,组织比较稳定.图 3给出经过3 000 s较长时间退火后的金相组织也正说明这一点,此时再结晶已经完全完成,晶粒为等轴状,分布比较均匀,晶粒没有发生明显粗化,平均晶粒尺寸为3 mm.
图 4为12道次超细晶纯Cu在150 ℃退火时微观结构随时间变化的TEM组织形貌.图(a)的晶粒细小且基本呈等轴结构,平均晶粒尺寸约250 nm,具有高的位错密度.退火200 s时由于时间较短,晶粒尺寸没有明显变化,但小部分晶粒开始发生再结晶(图 4(b)箭头所示),位错胞数量开始减少.随着退火时间的增加,在退火600 s时可以看出晶粒尺寸明显增加并出现了再结晶晶粒,平均晶粒尺寸约为1.4 μm,见图 4(c),产生的主要原因是由于超细晶材料内的储存能能满足进一步再结晶的能量条件.当退火3 000 s时,平均晶粒尺寸达3 mm,出现一些尺寸较大的退火孪晶(如图 4(d)中箭头所指).随着退火时间的变化材料发生了回复、再结晶和晶粒长大,试样发生了不同程度的软化,材料的硬度从146 HV降到73 HV.

|
图 4 12道次ECAP超细晶纯Cu在150 ℃经不同时间温退火后的TEM形貌 Fig.4 TEM morphology of 12 passes of ECAP ultra-fine pure copper after annealing at 150 ℃ for different time:(a)ECAPed; (b)200 s; (c)600 s; (d)3 000 s |
从上述等温退火的硬度变化和组织变化分析可以看出,在退火过程中由静态回复引起硬度变化几乎可以忽略,硬度变化主要与再结晶有关.
再结晶是一个热激活过程,这一过程要受到再结晶形核率(
| $ X=1-\exp \left[-\left(\frac{t}{t_{R}}\right)^{q}\right], $ | (1) |
| $ t_{R} ∞ \exp \left(\frac{Q_{R}}{K T}\right). $ | (2) |
式中:QR为再结晶的表观激活能;tR为一定体积分数下的再结晶时间.某瞬间dt再结晶体积分数变化量dX可用再结晶形核率(
| $ X=1-\exp \left(-\frac{\pi}{3} \dot{N} v^{3} t^{4}\right). $ | (3) |
则
| $ t=\sqrt{\frac{3 \ln (1-X)}{\pi \dot{N} v^{3}}}, $ | (4) |
| $ t_{R}=\frac{1}{\sqrt{\frac{4 \pi}{3} \dot{N} v^{3}}}. $ | (5) |
再结晶包括再结晶晶核形成和晶粒长大这两个过程,都是热激活过程.式(3)体现了再结晶时间是由形核速率(
| $ \dot{N}=N_{0} \exp \left(-\frac{Q_{\dot{N}}}{R T}\right), $ | (6) |
| $ v=v_{0} \exp \left(-\frac{Q_{v}}{R T}\right). $ | (7) |
将式(6)与(7)代入式(4)可得
| $ t=\sqrt{\frac{3 \ln (1-X)}{\pi \dot{N} v^{3}}} \cdot \exp \left(\frac{3 Q_{v}+Q_{\dot{N}}}{4 R T}\right). $ | (8) |
将式(6)和(7)联立式(2)和(5)可得
| $ Q_{R}=\frac{3 Q_{v}+Q_{\dot{N}}}{4}. $ | (9) |
若体积分数(X)为定值,则可写作Arrhenius公式的形式
| $ r_{R}=A_{0} \exp \left(\frac{Q_{R}}{R T}\right). $ | (10) |
式中:A0为常数;QR为再结晶激活能;T为绝对温度,K;R为气体常数,8.314 J/(mol·K).对式(10)两边取对数可写为
| $ \ln t_{R}=\ln A_{0}+\left(\frac{Q_{R}}{R}\right) \cdot\left(\frac{1}{T}\right). $ | (11) |
因此,ln t和1/T二者呈线性关系,根据式(11)做lnt~1/T坐标图并对其线形回归,其中QR/R为直线的斜率,从而根据不同温度下完成相同再结晶体积分数所需时间的比值就可得到材料的再结晶激活能(QR).
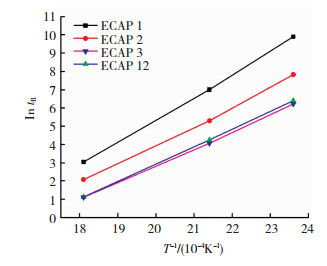
再结晶体积分数通过观测不同温度和不同时间的合金组织,采用定量金相技术来测定.因为硬度也可有效地反映合金再结晶规律,所以并参考测量不同温度、不同时间下硬度变化来确定超细晶铜在不同温度下退火的再结晶体积分数形成所需时间,如图 5为各道次超细晶铜的再结晶体积分数约为X=60%时,再结晶时间对数与温度1/T的关系曲线.从图 5可以看出,ECAP变形后各道次的区域稳定再结晶晶核形成的时间长短不相同.随着变形道次增大,退火温度升高,再结晶晶核形成所需时间就越短.主要是因为再结晶过程是形核与长大的过程,此过程是通过原子扩散来实现的,再结晶晶核要稳定长大必须满足再结晶晶核尺寸大于临界晶核的尺寸.而变形量愈大,临界晶核的尺寸愈小,因而变形量愈大,原子扩散愈容易,形成稳定晶核的尺寸愈小愈易形成稳定晶核,因此,再结晶形核的孕育期愈短.
|
图 5 再结晶时间对数与温度1/T的关系 Fig.5 Relationship between recrystallization time logarithm and temperature 1/T |
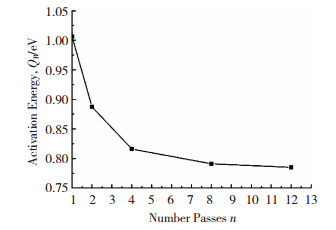
由图 5再结晶时间对数与温度1/T的关系可以看出,ln t与1/T呈直线关系,并且直线斜率为K(K=Q/R),经计算各道次变形后超细晶Cu的再结晶激活能见图 6.
|
图 6 超细晶Cu再结晶激活能QR Fig.6 Ultra-fine grain copper recrystallization activation energy QR |
从图 6可以看出,随变形道次的升高再结晶激活能降低,1道次超细晶Cu的激活能约为1 eV,12道次超细晶Cu的激活能约为0.78 eV.通常对于常规纯铜Qv≈QN≈1 eV,由式(9)也可得QR≈1 eV,Jägle等[18]测得高压扭转变形后铜的再结晶激活能为0.98 eV(94.4 kJ/mol).相似的结果也被许多研究所报道[19-20],通常冷加工变形铜的再结晶激活能约为1 eV.而Kunz等和Roodposhti等[21-22]研究发现,ECAP变形后超细晶Cu的再结晶激活能却较低,这是因为再结晶晶核优先发生在位错、空位等结构缺陷位置.随着变形量的增大,晶粒内部的储存能越大,再结晶倾向就越大,使得合金晶界处的位错、空位等结构缺陷密度增大,一方面为后续合金再结晶提供了有利的形核位置,也为原子的扩散提供有利的通道;另一方面,位错、空位等结构缺陷处的原子之间引力减弱,再结晶时原子扩散克服原子之间引力所消耗的能量(热垒)就会减小.因此,变形量越大,合金组织内部畸变能越高,再结晶形核激活能越低.由于包含大量位错的非平衡晶界提高了晶界扩散和原子移动,使Cu经过大变形后,没进行退火变形材料内部就已存在动态再结晶晶粒,同时变形材料内部还分散了当量的高角度晶界,因此,不需要形核的热激活能,在退火过程中很容易发生晶界的移动,随变形道次的增大,形核激活能
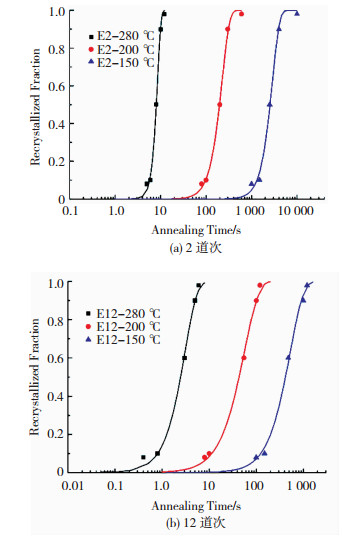
图 7为2道次和12道次ECAP变形后超细晶Cu在各个温度下对应的再结晶动力学曲线.同一变形量下,退火温度升高使得再结晶形核孕育时间缩短,完成再结晶所用的时间减少;但同一温度下退火,再结晶孕育期随着变形量的增大而缩短.再结晶开始时的速度较小,但随着再结晶的进行再结晶速度逐渐加快,在2道次变形后,再结晶体积分数在10%~85%时,其速度最大,在12道次变形后,再结晶体积分数在20%~80%时,速度达到最大,之后又逐渐减慢,直至再结晶结束.
|
图 7 再结晶动力学曲线 Fig.7 Kinetic curves of recrystallization: (a) 2 passes; (b) 12 passes |
1) 在相同退火温度条件下,随变形道次的增加,超细晶Cu的软化速度加快,在150 ℃时,1道次变形后的超细晶铜在20 h之后才基本趋于稳态,而12道次在0.5 h后就已达到稳态.随着退火温度的提高,再结晶速率增大,12道次变形后,超细晶铜在150 ℃时完成再结晶时间约为1 200 s,200 ℃时完成再结晶时间缩短至600 s,280 ℃时仅需50 s完成再结晶.
2) 超细晶Cu等温退火过程硬度变化可分为3个阶段:第1阶段,硬度略微下降为回复阶段;第2阶段,硬度急剧下降,开始发生再结晶;第3阶段,硬度逐渐稳定,再结晶完成.经12道次ECAP变形后,铜的晶粒尺寸细化到~250 nm,硬度达146 HV;在150 ℃等温退火后,600 s时平均晶粒尺寸约为1.4 μm,3 000 s时增长到3 μm.
3) 随着变形道次的增大,再结晶激活能越小,1道次超细晶铜再结晶激活能约为1 eV,12道次为0.78 eV.同一变形量下,退火温度越高,完成再结晶所用的时间越短;同一退火温度下,变形量增大,再结晶孕育期缩短,再结晶越容易发生.
| [1] |
章震威, 王军丽, 张清龙, 等. 等通道转角挤压制备超细晶材料的研究与发展[J]. 材料导报, 2017, 31(1): 116-125. ZHANG Zhenwei, WANG Junli, ZHANG Qinglong, et al. Research and development of ultra-fine grained materials prepared by equal channel angular extrusion[J]. Materials Review, 2017, 31(1): 116-125. DOI:10.11896/j.issn.1005-023X.2017.01.016 |
| [2] |
KIM Y G, KO Y G, SHIN D H, et al. Effect of equal-channel angular pressing routes on high-strain-rate deformation behavior of ultra-fine-grained aluminum alloy[J]. Acta Materialia, 2010, 58(7): 2545-2554. DOI:10.1016/j.actamat.2009.12.041 |
| [3] |
LATIEF F H, SUN I H. Effect of pressing routes on the microstructure and strength in equal channel angular pressing of Cu-3.75Ag[J]. Metals & Materials International, 2015, 21(4): 746-752. DOI:10.1007/s12540-015-5012-7 |
| [4] |
ZHANG Yue, WANG Jingtao, CHENG Chang, et al. Stored energy and recrystallization temperature in high purity copper after equal channel angular pressing[J]. Journal of Materials Science, 2008, 43(23-24): 7326-7330. DOI:10.1007/s10853-008-2903-8 |
| [5] |
SAKAI T, BELYAKOV A, KAIBYSHEV R, et al. Dynamic and post-dynamic recrystallization under hot, cold and severe plastic deformation conditions[J]. Progress in Materials Science, 2014, 60(1): 130-207. DOI:10.1016/j.pmatsci.2013.09.002 |
| [6] |
HUMPHREYS F J, HATHERLY M. Recrystallization and related annealing phenomena (Second Edition)[M]. Elsevier, 2004. DOI:10.1016/B978-008044164-1/50015-3
|
| [7] |
JAYAKUMAR P K, BALASUBRAMANIAN K, TAGORE G R. Recrystallisation and bonding behaviour of ultra fine grained copper and Cu-Cr-Zr alloy using ECAP[J]. Materials Science & Engineering A, 2012, 538(3): 7-13. DOI:10.1016/j.msea.2011.12.069 |
| [8] |
ABIB K, AZZEDDINE H, TIRSATINE K, et al. Thermal stability of Cu-Cr-Zr alloy processed by equal-channel angular pressing[J]. Materials Characterization, 2016, 118: 527-534. DOI:10.1016/j.matchar.2016.07.006 |
| [9] |
WANG Yali, LAPOVOK R, WANG Jingtao, et al. Thermal behavior of copper processed by ECAP with and without back pressure[J]. Materials Science & Engineering A, 2015, 628: 21-29. DOI:10.1016/j.msea.2015.01.021 |
| [10] |
王庆娟, 王清平, 杜忠泽. 等径弯曲通道变形制备超细晶铜的力学行为[J]. 特种铸造及有色合金, 2011, 31(10): 887-890. WANG Qingjuan, WANG Qingping, DU Zhongze. Mechanical behavior of ultrafine grained copper deformed by equal channel bending channel[J]. Special Casting and Nonferrous Alloys, 2011, 31(10): 887-890. DOI:10.3870/t222.2011.10.002 |
| [11] |
姜庆伟, 刘印, 王尧, 等. 超细晶铜在退火与高温变形条件下微观结构的不稳定性研究[J]. 金属学报, 2009, 45(7): 873-879. JIANG Qingwei, LIU Yin, WANG Yao, et al. Microstructure instability of ultra-fine grain copper during annealing and high temperature deformation[J]. Acta Metallurgica Sinica, 2009, 45(7): 873-879. DOI:10.3321/j.issn:0412-1961.2009.07.017 |
| [12] |
LUGO N, LIORCA N, SUNOL J J, et al. Thermal stability of ultrafine grains size of pure copper obtained by equal-channel angular pressing[J]. Journal of Materials Science, 2010, 45(9): 2264-2273. DOI:10.1007/s10853-009-4139-7 |
| [13] |
MOLODOVA X, GOTTSTEIN G, WINNING M, et al. Thermal stability of ECAP processed pure copper[J]. Materials Science & Engineering A, 2007, 460-461(1): 204-213. DOI:10.1016/j.msea.2007.01.042 |
| [14] |
HOSEINI M, POURIAN M H, BRIDIER F, et al. Thermal stability and annealing behaviour of ultrafine grained commercially pure titanium[J]. Materials Science & Engineering A, 2012, 532(3): 58-63. DOI:10.1016/j.msea.2011.10.062 |
| [15] |
MIAO S, XIE Z M, ZHANG T, et al. Mechanical properties and thermal stability of rolled W-0.5 wt% TiC alloys[J]. Materials Science & Engineering A, 2016, 671: 87-95. DOI:10.1016/j.msea.2016.06.049 |
| [16] |
TOMELLINI M. Functional form of the Kolmogorov-Johnson-Mehl-Avrami kinetics for non-isothermal phase transformations at constant heating rate[J]. Thermochimica Acta, 2013, 566(16): 249-256. DOI:10.1016/j.tca.2013.06.002 |
| [17] |
SAUVAGE X, ENIKEEV N, VALIEV R, et al. Atomic-scale analysis of the segregation and precipitation mechanisms in a severely deformed Al-Mg alloy[J]. Acta Materialia, 2014, 72(72): 125-136. DOI:10.1016/j.actamat.2014.03.033 |
| [18] |
JÄGLE E A, MITTEMEIJER E J. The kinetics of and the microstructure induced by the recrystallization of copper[J]. Metallurgical & Materials Transactions A, 2012, 43(4): 1117-1131. DOI:10.1007/s11661-011-0959-6 |
| [19] |
ZHANG J L, TASAN C C, LAI M J, et al. Partial recrystallization of gum metal to achieve enhanced strength and ductility[J]. Acta Materialia, 2017, 135: 400-410. DOI:10.1016/j.actamat.2017.06.051 |
| [20] |
ABIB K, AZZEDDINE H, TIRSATINE K, et al. Thermal stability of Cu-Cr-Zr alloy processed by equal-channel angular pressing[J]. Materials Characterization, 2016, 118: 527-534. DOI:10.1016/j.matchar.2016.07.006 |
| [21] |
KUNZ L, LUKÁŠ P, PANTELEJEV L, et al. Stability of ultrafine-grained structure of copper under fatigue loading[J]. Procedia Engineering, 2011, 10(7): 201-206. DOI:10.1016/j.proeng.2011.04.036 |
| [22] |
ROODPOSHTI P S, FARAHBAKHSH N, Sarkar A, et al. Microstructural approach to equal channel angular processing of commercially pure titanium: A review[J]. Transactions of Nonferrous Metals Society of China, 2015, 25(5): 1353-1366. DOI:10.1016/s1003-6326(15)63734-7 |
 2019, Vol. 27
2019, Vol. 27


