2. 重庆工商大学 工程训练中心, 重庆 400069;
3. 制造装备机构设计与控制重庆市重点实验室(重庆工商大学), 重庆 400069
2. Engineering Training Center, Chongqing Technology and Business University, Chongqing 400069, China;
3. Design and Control Key Laboratory of Manufacturing Equipment Mechanism of Chongqing(Chongqing Technology and Business University), Chongqing 400069, China
近年来随着激光技术的不断发展和进步, 激光切割也成为切割行业的一匹黑马, 以其切割质量好、切割速度快、应用范围广等优势在现代制造业中占据了很大的市场.但是激光切割过程中, 工艺参数对被切割件的切缝宽度、切割面表面粗糙度、挂渣量等切割质量的影响非常大[1-2]。而随着市场竞争的不断激烈,需要产品的生产工艺过程越来越简单,为此,要求板料成型前的精确下料和成形后的精准切割,以减少切割后工件的再处理,保证直接使用,这必将对切口端面宏观形貌和端面质量提出更高的要求。因此,激光切割工艺参数对切割质量影响的研究显得尤为必要。
陈宇翔[3]、陈聪[4]、Scintica[5]、徐国建[6]和Madilla[7]等人分别以钢和铝合金为研究对象,研究了激光切割时辅助气体压力、离焦量、切割速度、激光功率等参数对切割后试样的挂渣厚度、切缝宽度、表面粗糙度等切割质量的影响。研究发现,针对激光切割工艺参数的优化研究主要集中在激光功率、切割速度、辅助气压、离焦量等参数,而切割质量的主要研究指标有切割后的挂渣厚度、切缝宽度、表面粗糙度等。为了准确研究激光功率、离焦量、辅助气体压力、切割速度等对切缝宽度、切割表面质量、挂渣量等切割质量因素的影响规律,确定最优的工艺参数,本试验采用响应面法以不同的激光功率、离焦量、辅助气体压力、切割速度作为设计变量,以最小切缝宽度、最小切割表面纹理、最小挂渣量为响应目标,建立了响应面模型,最终得到响应目标与各设计变量之间的数学模型。试验过程中,切缝宽度、切割表面纹理和挂渣量的测量及准确表达对研究结果具有至关重要的影响,本试验将采集大量的数据并运用合理的统计方法以保证试验结果的准确性。
1 试验 1.1 试验设备本试验采用ZT-J-55M连续光纤激光切割机(图 1),该设备发出的是一种高性能的连续激光,光电转换效率达到30%以上,最大激光功率500 W。

|
图 1 ZT-J-55M连续光纤激光切割机 Fig.1 ZT-J-55M continuous fiber laser cutting machine |
试验材料为3 mm厚的304不锈钢,切割过程采用氧气作为辅助气体。为了方便测量试样的切缝宽度、挂渣量以及表面纹理,将试样设计为如图 2所示的形状。
|
图 2 试样形状(单位:mm) Fig.2 Shape of sample |
本试验考察影响激光切割质量的主要因素包括:激光功率、离焦量、辅助气体压力、切割速度,因其对切割质量的影响不是独立的,本文采用响应面法进行试验设计。
响应面模型建立通过Design-Expert软件进行,采用中心组合设计(Central Composite Design,CCD)进行试验方案设计,试验选用激光功率、离焦量、辅助气体压力、切割速度4个因素,每个因素取5个水平,以(-2,-1,0,+1,+2)编码,选最窄切缝宽度、最小切割表面波纹度、最少挂渣量为响应目标, 设计因素及水平值见表 1,各因素的取值范围直接影响响应面模型的显著性,因此,所有因素的取值范围均基于前期单因素试验, 试验设计方案如表 2所示。
| 表 1 设计因素及水平值 Table 1 Variables and level values |
| 表 2 响应面试验设计 Table 2 Experiment design of response surface |
切割试样的切缝宽度、切割表面纹理和挂渣量均在Leica DVM6型超景深显微镜上进行测量,为保证测量结果的准确性,每组工艺参数切割两个试样,对目标参数均进行多次测量,然后进行数据处理,得到最终的测量结果。
2.1 切缝宽度的测量切缝宽度测量如图 3所示。在每个试样上等距选取9个位置进行切缝宽度的量取,共18组数据,并对数据进行格拉布斯异常值检验,见式(1)。剔除异常数据,将其他数据求平均,得到切缝宽度的最终数据d。
| $ \left| {{d_{\rm{p}}}} \right| = \left| {{x_{\rm{p}}} - \bar x} \right| > {G_{(\alpha , n)}}s. $ | (1) |

|
图 3 切缝宽度的测量 Fig.3 Measurementof kerfwidth |
式中:xp为测量数据;x为该组数据的算术平均值;G(α, n)为格拉布斯检验临界值,其与试验次数n和给定的显著水平α有关[8]。
| $ \bar d = \frac{{\sum\limits_{i = 1}^n {{d_i}} }}{n}, n \le 18. $ | (2) |
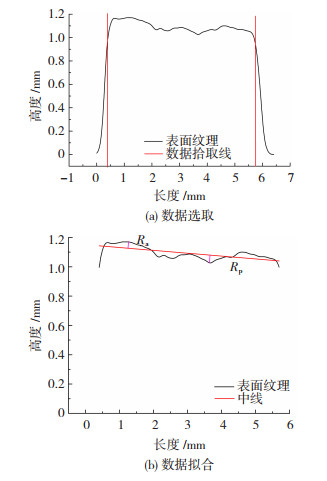
图 4所示为激光切割后试样切割表面的形貌,可以看出切割表面有明显的纹理,这是激光照射时金属受热熔化产生金属流动导致的,且纹理的分布有明显的分层,因此,在测量表面纹理时选用斜线取值,取值范围涵盖全部纹理分布区,最终得到斜线上各点的高度值,如图 5(a)所示,通过Matlab软件对已有数据编程处理,采用最小二乘法拟合出一条中线,中线以上的称为波峰,中线以下称为波谷,分别计算波峰和波谷的大小,即波峰到中线的距离Ra,波谷到中线的距离Rp, 选取最大波峰高度Ramax和最大波谷深度Rpmax之和RZ,用最大峰值RZ来表征切割表面纹理的大小,如图 5(b)所示。

|
图 4 表面纹理的测量 Fig.4 Measurement of surface texture |
|
图 5 表面纹理测量曲线 Fig.5 Measurement curve of surface texture:(a) data selection; (b) data fitting |
挂渣量用平均挂渣高度H0表征,采用多点测量求平均的方法获取H0,图 6(a)所示为切割试样测量挂渣量的位置分布,每个试样测量4次,即同一组工艺参数下获得试样挂渣量数据有8组。因超景深显微镜在测量不同表面的表面数据时很难确定一个统一的参考面,因此,单纯采用挂渣量的高度值无法精确表达挂渣量,需要测量挂渣量高度H1和非切割表面的高度H2两个数据,用挂渣量的相对高度H0来描述挂渣量的多少,见图 6(b)。
| $ {H_0} = {H_1} - {H_2}, $ | (3) |
| $ {\overline H _0} = \frac{{\sum\limits_{i = 1}^n {{H_{0i}}} }}{n}, n \le 8. $ | (4) |

|
图 6 挂渣量的测量位置分布(a)与测量方法(b) Fig.6 Measuring position of slag thickness and measurement |
采用以上测量方法,得到试验结果如表 3所示,表 3中Y1为切缝宽度,Y2为表面纹理,Y3为挂渣量。
| 表 3 响应面试验设计及结果 Table 3 Experiment design and result of response surface |
针对表 3结果通过拟合回归方程可以得到3个目标响应的预测函数,见式(5)、(6)、(7)。
| $ \begin{array}{l} {Y_1} = 0.15 + 0.0036{X_1} - 0.055{X_2} + 0.089{X_3} - \\ \;\;\;\;\;\;\;\;0.03{X_2}{X_3} + 0.04{X_3^2}, \end{array} $ | (5) |
| $ \begin{array}{l} {Y_2} = - 5.51 + 0.021{X_1} + 4.81{X_2} + 0.127{X_3} - \\ \;\;\;\;\;\;\;0.03{X_4} - 0.019{X_1}{X_2} - 0.005{X_1}{X_2} + \\ \;\;\;\;\;\;\;0.518{X_2}{X_3} - 0.00001{X_1}^2 - 0.543{X_2}^2 + \\ \;\;\;\;\;\;\;0.066{X_3^2} - 0.001{X_1}{X_2}{X_3} + 0.00001{X_1}^2{X_2} + \\ \;\;\;\;\;\;\;0.00001{X_1^2}{X_3} + 0.00001{X_1}{X_2}^2, \end{array} $ | (6) |
| $ \begin{array}{l} {Y_3} = 1.64 - 0.015{X_1} + 0.76584{X_2} + 0.0938{X_3} - \\ \;\;\;\;\;\;0.2209{X_4} - 0.0018{X_1}{X_2} - 0.005{X_1}{X_3} + \\ \;\;\;\;\;\;0.4887{X_2}{X_3} + 0.00004{X_1^2} - 0.00119{X_2}{X_3} + \\ \;\;\;\;\;\;0.00001{X_1^2}{X_3} - 2.5E - 008{X_1}{X_2^2}. \end{array} $ | (7) |
为了验证模型的可靠性,需对以上响应面模型进行显著性分析,表 4~6为应用方差分析得到的分析结果,结果显示3个模型的P值均小于0.000 1,远低于临界值0.05,说明模型非常显著。除了对模型的显著性分析,还要对模型的误差进行分析,误差分析结果见表 7,R2表示复相关系数,R2越大表示相关性越强,RAdj2表示校正复相关系数平方值,RPred2表示预测复相关系数平方值,RAdj2和RPred2可以表示模型拟合度的好坏,其值越接近1,且RAdj2-RPred2 < 0.2,说明模型拟合度高,误差小[9-11]。
| 表 4 切缝宽度方差分析 Table 4 Variance analysis of kerf width |
| 表 5 表面纹理方差分析 Table 5 Variance analysis of surface texture |
| 表 6 挂渣量方差分析 Table 6 Variance analysis of slag thickness |
| 表 7 模型误差分析 Table 7 Error analysis of model |
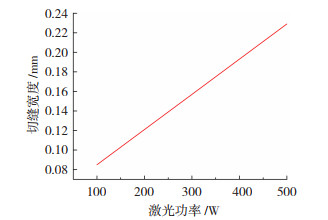
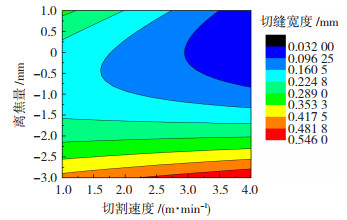
从表 4可以看出,激光功率和离焦量对切缝宽度的影响最为非常显著。图 7为X2=2.48 m/min, X3=-1.05 mm, X4=1 MPa时切缝宽度与激光功率之间的变化关系,可以看出随着激光功率的增加,切缝宽度不断增大,原因是金属在进行激光切割时,影响切缝宽度的因素主要取决于被熔化的金属量的多少,而被熔化金属的量则取决于施加在该处的激光能量的大小和能够吸收的激光能量的大小,对于同品种同厚度的材料,其激光吸收率、比热容以及熔化相变比焓确定不变,故单位时间内被熔化的金属质量取决于激光功率的大小[12]。图 8为X1=300 W, X4=1.2 MPa时切割速度和离焦量的相互作用对切缝宽度的影响,可以看出,随着切割速度的加快切缝宽度逐渐减小,随着离焦量的增大切缝宽度先减小后增大,原因是切割速度影响激光光束在同一切割位置停留的单位时间,切割速度越大,在切割处停留的时间则越小,该处熔化的金属越少,而离焦量对切缝宽度的大小影响更为直接,激光光束的焦点位置处能量最大,离焦点越远能量越小。图 9为离焦量对切缝宽度影响的示意图,以光束焦点在金属上表面认定为离焦量为零,在此之上为正,之下为负,那么离焦量从正到负变化,切缝宽度呈现由宽变窄又变宽的趋势。原因是在有效激光作用范围内,离焦点越远的地方光束越大,金属受热范围就越大,切缝宽度越宽。
|
图 7 激光功率对切缝宽度的影响 Fig.7 Influence of laser power for kerf width |
|
图 8 切割速度和离焦量的交互作用对切缝宽度的影响 Fig.8 Influence of cutting speed and focus positions for kerf width |
|
图 9 离焦量对切缝宽度的影响示意图 Fig.9 Sketch map of influence of focus positionson kerf width |
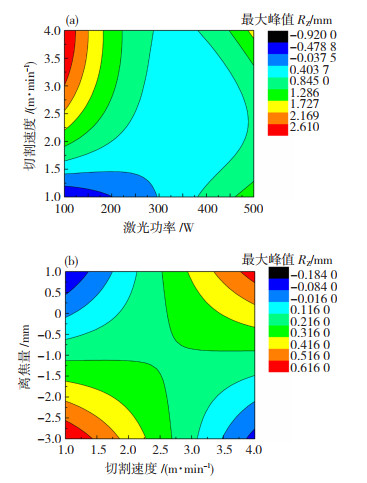
图 10为X1=300 W, X3=0 mm, X4=1.40 MPa时激光功率和切割速度,以及离焦量和切割速度对切割表面纹理的影响,可以看出表面纹理的最大波峰值RZ随着激光功率、离焦量以及切割速度的增大先减小后增大,原因是激光功率和离焦量的大小直接决定了某处金属受热量的大小[13],即决定了金属的熔化量,而金属的熔化、凝固势必会在切割表面形成纹理,因此,激光功率和离焦量对表面纹理的影响显著。
|
图 10 X1X3(a)、X2X3(b)的交互作用对表面纹理的影响 Fig.10 Influence of X1X3(a)、X2X3(b) on surface texture |
从表 5可以看出辅助气体压力对表面纹理的影响也显著,原因是:在激光切割过程中,由于辅助气体为氧气使得切割过程中氧化反应比较剧烈,氧化反应释放大量的热量加速了金属的熔化[14],如果切割速度比较慢,那么切割位置的氧化反应剧烈,容易造成过烧,表面纹理最大波峰值就大,相反,表面纹理则平缓。因此,在金属激光切割过程中,氧气对表面纹理的影响是起促进还是抑制作用,主要取决于氧化和冷却速度谁更快,因此,辅助气体压力和切割速度对表面纹理的影响是显著的。
3.3 工艺参数对挂渣量的影响从表 6挂渣量的方差分析中可以发现,激光功率和切割速度对挂渣量的影响非常显著,离焦量和辅助气体压力对挂渣量的影响也较显著,挂渣形成的主要原因是金属在受到激光光束照射时受热熔化,受到重力的作用向金属下表面流动,由于光束照射时间(取决于切割速度)比较短,因此熔化的金属部分来不及掉落而凝固在金属下表面。因此,激光功率的大小和切割速度的快慢直接影响挂渣量的大小[15]。而离焦量的大小决定了金属受热集中区离下表面的距离,辅助气体由于一定压力的存在可以有效地吹走熔化的金属,可以减少挂渣量,因此,挂渣量的大小与4个因素都相关。
3.4 工艺参数优化采用Design-Expert软件自带的优化功能Numerical对激光切割工艺参数进行优化,设计优化条件为切缝宽度、表面纹理的最大峰值RZ、挂渣量三者均最小,设置切缝宽度的上下限范围为0~0.426 844 mm,表面纹理的最大峰值RZ的范围为0~0.226 402 mm,挂渣量的范围为0~0.550 358 mm,得到最佳切割工艺参数为:X1=365.86 W, X2=2.75 m/min, X3=0 mm, X4=1.4 MPa,响应目标为Y1=0.127 183 mm, Y2=0.106 431 mm, Y3=0.094 022 1 mm,满意度为0.967.对优化参数进行切割验证,为了保证结果的正确性,采用3次切割验证并进行数据测量,得到表 8所示的数据,切缝宽度的预测误差控制在8.4%~12.7%,表面纹理最大峰值的预测误差在21%~24.9%,挂渣量的预测误差控制在16.7%~19.5%,验证了预测函数的正确性,图 11为验证试样的部分测量图。
| 表 8 验证试样的数据 Table 8 Verification of the sample data |

|
图 11 验证试样切割质量 Fig.11 Verification of the sample′s cutting quality |
1) 采用响应面中心组合设计法设计试验,建立了四因素五水平的响应面模型,得到了切缝宽度、表面纹理最大峰值、挂渣量的预测模型,结果表明:切割速度、离焦量、激光功率对切缝宽度的影响显著,激光功率、切割速度、离焦量、辅助气体压力对表面纹理的最大峰值、挂渣量的影响均显著。
2) 采用Design-Expert软件以切缝宽度、表面纹理最大峰值、挂渣量均最小为优化目标进行优化,得到了最佳切割工艺参数,X1=365.86 W, X2=2.75 m/min, X3=0 mm, X4=1.4 MPa,并通过试验验证,误差均控制在25%以内。
| [1] |
LIBRERA E, RIVA G, SAFARZADEH H, et al. On the use of areal roughness parameters to assess surface quality in laser cutting of stainless steel with CO2 and fiber sources[J]. Procedia CIRP, 2015, 33: 532-537. DOI:10.1016/j.procir.2015.06.069 |
| [2] |
CHOUBEY A, JAIN RK, ALI S, et al. Studies on pulsed Nd:YAG laser cutting of thick stainless steel in dry air and underwater environment for dismantling applications[J]. Optics & Laser Technology, 2015, 71: 6-15. DOI:10.1016/j.optlastec.2015.02.007 |
| [3] |
陈宇翔, 高亮. 正交法分析激光切割高温合金钢工艺参数[J]. 激光与光电子学进展, 2016(11): 210-218. CHEN Yuxiang, GAO Liang. Analysis of processing parameters for laser cutting high-temperature alloy steel by orthogonal method[J]. Laser& Optoelectronics Process, 2016(11): 210-218. |
| [4] |
陈聪, 高明, 顾云泽, 等. 光纤激光切割铝合金薄板工艺特性研究[J]. 中国激光, 2014(6): 79-85. CHEN Cong, GAO Ming, GU Yunze, et al. Study on fiber laser cutting of aluminum alloy sheet[J]. Chinese Journal of Lasers, 2014(6): 79-85. |
| [5] |
SCINTILLA L D. Continuous-wave fiber laser cutting of aluminum thin sheets: Effect of process parameters and optimization[J]. Optical Engineering, 2014, 53(6): 066113. DOI:10.1117/1.OE.53.6.066113 |
| [6] |
徐国建, 李宏利, 杭争翔, 等. 6 mm碳钢板的激光切割性能[J]. 激光与光电子学进展, 2014(4): 43-48. XU Guojian, LI Hongli, HANG Zhengxiang. Performance of 6 mm mild steel sheet laser cutting[J]. Laser & Optoelectronics Process, 2014(4): 43-48. |
| [7] |
MADIC M, RADOVANOVIC M, NEDICB B. Modeling and simulated annealing optimization of surface roughness in CO2 laser nitrogen cutting of stainless steel[J]. Tribology in Industry, 2013, 35(3): 167-176. |
| [8] |
李云雁, 胡传荣. 试验设计与数据处理[M]. 北京: 化工出版社, 2017. LI Yunyan, HU Chuanrong. Test design and data processing[M]. Beijing: Chemical Industry Press, 2017. |
| [9] |
李莉, 张赛, 何强, 等. 响应面法在试验设计与优化中的应用[J]. 实验室研究与探索, 2015(8): 41-45. LI Li, ZHANG Sai, HE Qiang, et al. Application of response surface methodology in experimental design and optimization[J]. Research and Exploration in Laboratory, 2015(8): 41-45. |
| [10] |
崔磊, 刘静, 李兰云. 基于响应面法的双层316L/Inconel625波纹管液压胀形工艺参数优化[J]. 兵器材料科学与工程, 2018(6): 19-26. CUI Lei, LIU Jing, LI Lanyun. Optimization of hydroforming process parameters of bi-layered 316L/Inconel625 bellows based on response surface method[J]. Ordnance Material Science and Engineering, 2018(6): 19-26. DOI:10.14024/j.cnki.1004-244x.20181101.001 |
| [11] |
王梦寒, 黄龙, 王瑞, 徐志敏. 基于响应面法的铝合金筋板锻件工艺参数多目标优化[J]. 材料科学与工艺, 2014, 22(1): 123-128. WANG Menghan, HUANG Long, WANG Rui, et al. Multi-objective optimization of process parameters by RSM for aluminium-alloy rib-web forgings[J]. Materials Science and Technology, 2014, 22(1): 123-128. |
| [12] |
冯巧波, 赵旺初, 李永兵. 工艺参数对不锈钢薄板激光切割质量的影响[J]. 机械设计与研究, 2017(6): 118-121. FENG Qiaobo, ZHAO Wangchu, LI Yongbing. Effect of technological parameters on laser cutting quality of stainless steel sheet[J]. Mechanical Design and Research, 2017(6): 118-121. DOI:10.13952/j.cnki.jofmdr.2017.0255 |
| [13] |
彭玉海, 赵晋平, 侯红玲, 等. 工艺参数对2A12铝合金激光切割质量的影响及分析[J]. 应用激光, 2016(1): 78-83. PENG Yuhai, ZHAO Jinping, HOU Hongling, et al. The influence and analysis to process parameter on the laser cutting quality of 2Al2 aluminum alloy[J]. Applied Laser, 2016(1): 78-83. |
| [14] |
ABDEL GHANY K, NEWISHY M. Cutting of 1.2mm thick austenitic stainless steel sheet using pulsed and CW Nd:YAG laser[J]. Journal of Materials Processing Technology, 2005, 168(3): 438-447. DOI:10.1016/j.jmatprotec.2005.02.251 |
| [15] |
王威.中厚钢板激光氧气切割特性与机理研究[D].北京: 机械科学研究总院, 2015. WANG Wei. The characteristics and mechanism of high-power solid state laser cutting of thick steel platewith oxygen[D]. Beijing: China Academy of Machinery Science and Technology, 2015. http://cdmd.cnki.com.cn/Article/CDMD-82701-1015408820.htm |
 2020, Vol. 28
2020, Vol. 28


