2. 燕山大学 机械工程学院,河北 秦皇岛 066004;
3. 秦皇岛市液压胀形工程技术研究中心,河北 秦皇岛 066000;
4. 中国重型汽车集团有限公司,济南 250101
2. School of Mechanical Engineering, Yanshan University, Qinhuangdao 066004, China;
3. Qinhuangdao Hydroforming Engineering Technology Research Center, Qinhuangdao 066004, China;
4. China National Heavy Duty Truck Group Co., LTD., Jinan 250101
液压胀形技术减轻了零件重量、提高了零件强度,已广泛应用于汽车、航空、航天等领域的零部件制造过程[1-2]。加载路径即轴向进给量与液体内压的关系,是影响液压胀形的重要因素,二者关系匹配不当会导致管坯发生开裂或失稳起皱[3]。Aydemir等人[4]运用了一种自适应的分析方法对T形管件进行了加载路径的优化,并用有限元软件模拟获得了符合要求的合格件。吴娜等人[5]提出了基于均匀增容的液压胀形加载路径的设计方法,并试制出大型汽车桥壳预成形管坯,样件成品率高、成形性好。
极限胀形系数(管坯胀形后的最大半径与胀形前半径的比值)对管材的液压胀形至关重要。Carleer等人[6]对管件的材料属性进行了深入研究,结果表明,材料各向异性系数和硬化指数的数值越大,其管材自由胀形高度越高,轴向缩进量越大。张庆等人[7]推导了薄壁管极限胀形系数,并提出通过模拟获得胀形成形极限应变及极限胀形系数的方法。王连东等人[8]通过对汽车桥壳样件的液压胀形胀裂试验,绘制出了不同加载路径下的胀形极限图,给出了胀裂判据。
现有的液压胀形研究,大部分将管坯设定为壁厚均匀,但由于轧制芯棒磨损、轧制芯棒与轧辊的位置偏差及变形过程中管材加热不均等原因,管坯内外圆不同心,导致壁厚存在一定偏差。Shirayori等人[9-10]在研究管材的初始壁厚偏差对自由液压胀形的影响时发现,自由胀形过程中壁厚偏差的增加与管材材料和管端边界条件有关。杨连发等人[11]将壁厚偏差为0~20%、规格为Φ32 mm×0.75 mm的A6063铝合金无缝管于400 ℃下退火3 h后,在专用设备上进行了两端自由液压胀接试验,胀形区长度为40 mm,结果表明胀形过程中管坯截面存在畸变,初始壁厚偏差越大,畸变越严重,内外轮廓偏心距越大。He等人[12]研究了具有不同初始壁厚偏差的薄壁管的液压胀形,发现薄壁管的变形行为和成形极限与初始壁厚偏差关系很大,初始壁厚偏差越大,变形截面轮廓差异越大。上述研究是小径薄壁管在特定条件下进行的自由液压胀形。
针对汽车桥壳这种截面复杂的大型管类件,燕山大学课题组提出了汽车桥壳胀压成形新工艺。选用一定规格的热轧无缝钢管作为初始管坯,对其两端进行缩径后,再对其中部进行大变形液压胀形,得到预成形管坯;最后对其内部充液(水)并用模具压制成形,得到带有球冠状后盖及前盖的桥壳管件[13-14]。作者在使用壁厚允许偏差为±10%的热轧无缝钢管(GB/T 8163-2018)进行汽车桥壳大变形液压胀形试验时,发现管坯存在开裂、褶皱现象,产品合格率较低,而关于壁厚偏差对液压胀形过程影响的研究尚未见文献报道。因此本文针对带壁厚偏差管坯液压胀形,揭示不同轴向应力状态下壁厚偏差对液压胀形的影响,并给出带壁厚偏差管坯液压胀形的设计标准;结合有限元模拟确定带壁厚偏差管坯液压胀形的加载方式,并在专用液压机上进行试验验证。
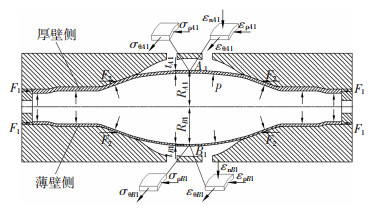
1 带壁厚偏差管坯液压胀形力学分析基于文献[15]建立带有壁厚偏差的热轧无缝钢管几何模型,建立带壁厚偏差管坯胀形初始时的力学模型,并沿周向对管坯中心截面进行剖切,如图 1所示。胀形区初始外径为d,厚壁侧壁厚为t1,薄壁侧壁厚为t2,胀形区中部与两侧锥面过渡处外圆角为r。胀形时在管坯端部施加轴向推力F1,在过渡锥面处施加轴向推力F2,内压为p。

|
图 1 带壁厚偏差管坯胀形初始时力学模型 Fig.1 Initial mechanical model of bulging tube with wall thickness deviation |
对管坯施加外力和内压后,胀形区各质点处于平面应力状态:轴向应力σρ和周向应力σθ,拉应力时取正值,压应力时取负值。在胀形区内截取单元体,将力沿曲面法线方向投影,则由平衡条件可得
| $ \frac{p}{t} - \frac{{{\sigma _{\rm{ \mathsf{ θ} }}}}}{{{R_{\rm{ \mathsf{ θ} }}}}} - \frac{{{\sigma _{\rm{ \mathsf{ ρ} }}}}}{{{R_{\rm{ \mathsf{ ρ} }}}}} = 0 $ | (1) |
式中:Rθ为周向剖面曲率半径,胀形初始时,Rθ为管坯外径的一半;Rρ为纵向剖面曲率半径,对于外凸曲线,Rρ取正值,对于内凹曲线,Rρ取负值;t为单元体处管坯壁厚。
变形时塑性变形条件按Mises准则,即应满足
| $ \sigma _{\rm{ \mathsf{ θ} }}^{\rm{2}} - {\sigma _{\rm{ \mathsf{ θ} }}}{\sigma _{\rm{ \mathsf{ ρ} }}} + \sigma _{\rm{ \mathsf{ ρ} }}^{\rm{2}} = \sigma _{\rm{s}}^{\rm{2}} $ | (2) |
其中,轴向应力σρ为
| $ {\sigma _{\rm{ \mathsf{ ρ} }}} = - \frac{{{F_1} + {F_2} - \frac{{\rm{ \mathsf{ π} }}}{4}{{(d - 2t)}^2}p}}{{{\rm{ \mathsf{ π} d}}t}} $ | (3) |
由式(1)和式(3)可知,σρ由模具施加给管坯的轴向推力和液体内压共同产生,σρ不同,胀形区各点发生塑性变形所需的内压不同,即变形顺序不同。
当轴向应力σρ=0时,胀形区两侧锥面过渡处与中部发生塑性变形所需的内压相同,两侧与中部同时胀形扩径。则厚壁侧、薄壁侧发生塑性变形所需的内压分别为
| $ {p_A} = \frac{{2{t_1}}}{d}{\sigma _{{\rm{ \mathsf{ θ} }}A}} $ | (4) |
| $ {p_B} = \frac{{2{t_2}}}{d}{\sigma _{{\rm{ \mathsf{ θ} }}B}} $ | (5) |
胀形初始时胀形区各点屈服极限相同,由式(2)可知各点周向应力也相同。因t1>t2,故A点变形所需的内压高于B点,而实际上在胀形过程中管坯内部各点受到相同的内压作用,故薄壁侧会早于厚壁侧先胀形,若变形量过大,将导致薄壁侧因减薄率过大而早于厚壁侧胀裂。
当轴向应力σρ>0,即轴向推力相对液体内压较小时,对于薄壁侧,胀形区两侧锥面过渡处C点发生塑性变形所需的内压为
| $ {p_C} = \frac{{2{t_2}}}{d}{\sigma _{{\rm{ \mathsf{ θ} }}C}} + \frac{{{t_2}}}{r}{\sigma _{{\rm{ \mathsf{ ρ} }}C}} $ | (6) |
因中部B点纵向曲率半径趋近于无穷大,故B点发生塑性变形所需的内压仍按式(5)确定。因胀形初始时胀形区各点的屈服极限、轴向应力及周向应力相同,比较式(6)与式(5)可知:由于胀形区两侧过渡处存在外凸圆角r,C点(D点)发生塑性变形所需的内压大于中部B点的内压,产生中部高于两侧的单鼓形(见图 2),而且r越小以及σρ拉应力数值越大,单鼓形越突出,厚壁侧变形与薄壁侧类似。对于中部,由于壁厚偏差,薄壁侧仍将早于厚壁侧胀形扩径,单鼓形更突出,轴向补料效果更差,会更早的胀裂,极限胀形系数更低。
|
图 2 单鼓胀形时力学模型 Fig.2 Mechanical model of single drum bulging |
当轴向应力σρ < 0,即轴向推力相对液体内压较大时,对于薄壁侧,胀形区两侧过渡处C点及中部B点发生变形所需的内压仍按式(6)和式(5)确定。因胀形初始时胀形区各点的屈服极限、轴向应力及周向应力相同,比较式(6)与式(5)可知:由于胀形区两侧过渡处存在外凸圆角r,C点(D点)发生塑性变形所需的内压小于中部B点的内压,产生中部低于两侧的双鼓形(见图 3),而且r越小以及压应力σρ数值越大,双鼓形越突出,两侧与中部之间落差Δ越大,当Δ达到某一值时,中部可能因补料过多发生失稳形成褶皱,厚壁侧变形与薄壁侧类似。由于壁厚偏差,薄壁侧也将早于厚壁侧胀形扩径,但厚壁侧双鼓形更突出,中部补料更多,更容易失稳形成褶皱。

|
图 3 双鼓胀形时力学模型 Fig.3 Mechanical model of double drum bulging |
由以上分析可知,在壁厚偏差管坯液压胀形过程中轴向应力为压应力时有助于金属向胀形区中部流动,弱化壁厚偏差的影响,但轴向压应力过大会使胀形区失稳形成褶皱,因此在轴向压应力增大至一定值后需同时增大液体内压,从而得到符合工艺要求的管坯。
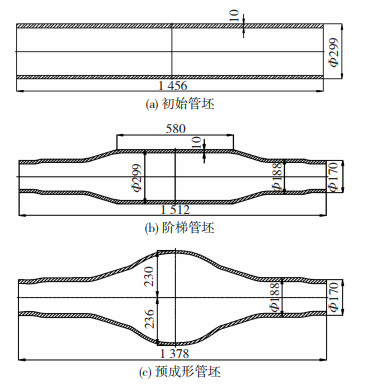
2 液压胀形有限元模拟 2.1 研究对象以某重型卡车桥壳预成形管坯的液压胀形工艺为研究对象,首先选用长度为1 456 mm,外径和壁厚为Φ299 mm×10 mm的热轧Q345B无缝钢管作为初始管坯(图 4(a));左右两端经过一定量的缩径后,得到长度为1 512 mm,中间胀形区长度为580 mm,直臂外径为Φ188 mm,端部外径为Φ170 mm的阶梯管坯(图 4(b))。再对其进行整体退火处理,然后在内压和轴力的共同作用下,通过液压胀形,使其中部胀起,得到长度为1 378 mm,上侧最高点距中心230 mm,下侧最高点距中心236 mm的预成形管坯(图 4(c)),最大胀形系数为
|
图 4 预成形工艺过程(单位: mm) Fig.4 Performed process: (a)initial tube; (b)stepped tube; (c)performed tube |
选取退火后的初始管坯样件进行拉伸试验,得到管坯屈服极限为315 MPa,强度极限为500 MPa,弹性模量E=2.1×105 MPa,泊松比υ=0.3,密度ρ=7.8×103 kg/m3,伸长率A=24%,硬化指数n=0.2,各向同性材料真实应力-应变关系为σ=900ε0.2。
基于桥壳产品前后对称,左右不对称,故在ABAQUS软件中使用1/2管坯和模具型腔对管坯进行缩径和液压胀形模拟,在管坯的纵向截面上设置对称约束,缩径模具及胀形模具都设定为刚体,管件与模具间建立刚-柔接触,采用缩减积分单元C3D8R沿管壁方向分两层对管坯进行网格单元划分。根据胀形前后等体积原则并结合实际经验,确定胀形过程单侧模具轴向推进量为S=67 mm。
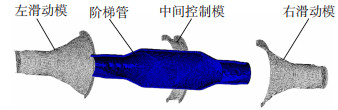
设定周向壁厚偏差ω分别为0.2、0.5和0.8 mm的3种初始管坯,按图 4所示的工艺过程,两端经过缩径后得到阶梯管坯,然后重新导入到ABAQUS中并赋予新的材料参数(相当于退火处理),建立半滑动式液压胀形有限元模型,如图 5所示。模拟时中间控制模设置为全约束,左、右滑动模沿轴线相对运动。
|
图 5 半滑动式液压胀形有限元模型 Fig.5 Finite element model of half-sliding hydroforming |
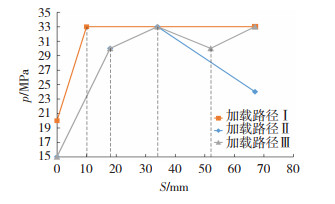
基于理论分析并结合大量的模拟给出3种典型的加载路径,如图 6所示。
|
图 6 内压-轴向推进量关系曲线 Fig.6 Pressure-shift curves under different loading paths |
加载路径Ⅰ:胀形过程中轴向应力σρ>0。具体过程如下:以较高内压20 MPa起胀,轴向推进10 mm时内压快速线性增加至33 MPa,并保持不变至合模,然后保压校形。
加载路径Ⅱ:胀形过程中轴向应力σρ < 0且不断增大。具体过程如下:以较低内压15 MPa起胀,轴向推进34 mm时内压分段阶梯线性增加至33 MPa,合模时再线性减小至24 MPa,然后保压校形。
加载路径Ⅲ:胀形过程中轴向压应σρ < 0且先增大后减小。具体过程如下:以较低内压15 MPa起胀,轴向推进34 mm时内压分段阶梯线性增加至33 MPa;轴向推进52 mm时内压线性减小至30 MPa;合模时再线性增加至33 MPa,然后保压校形。
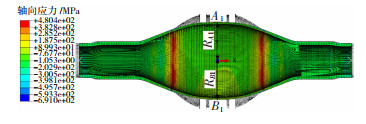
2.3.1 加载路径Ⅰ下模拟结果及分析壁厚偏差ω=0.5 mm的阶梯管参照加载路径Ⅰ在左、右滑动模推进至16 mm时,胀形区缓慢平直胀起;左、右滑动模推进至32 mm时,薄壁侧中部轴向应力已为拉应力,胀形快于两侧,呈单鼓形(见图 7);随着胀形的进行,厚壁侧也呈中部高于两侧的单鼓形;左、右滑模推进至49 mm时,A1点半径为218.2 mm,胀形系数kA1为1.46,壁厚为8.45 mm,减薄率ηA1为17.6%;B1点半径为222.8 mm,胀形系数kB1为1.49,壁厚为7.74 mm,减薄率ηB1为20.6%,即薄壁侧减薄率超过了开裂的近似判据值|εn|≤0.85 A[8]。该路径下不同ω管坯模拟结果见表 1。
|
图 7 加载路径Ⅰ下ω=0.5 mm时模拟结果 Fig.7 Simulation results of the tube blank with ω=0.5 mm at loading path Ⅰ |
| 表 1 加载路径Ⅰ下不同ω管坯破裂时模拟结果 Table 1 Simulation results of tube blanks with different ω ruptured at loading pathⅠ |
加载路径Ⅰ模拟结果表明:①壁厚偏差ω越大,薄壁侧单鼓形越突出,与厚壁侧变形差异越大。ω为0.2、0.5和0.8 mm的管坯破裂时,薄壁侧与厚壁侧最大半径差值分别为1.0、4.6和7.8 mm。②壁厚偏差ω越大,薄壁侧减薄越多,破裂越早,轴向补料越少,极限胀形系数越低。当ω由0.2 mm增至0.8 mm,模具工进量由54 mm减至45.5 mm,薄壁侧极限胀形系数由1.51减至1.47。
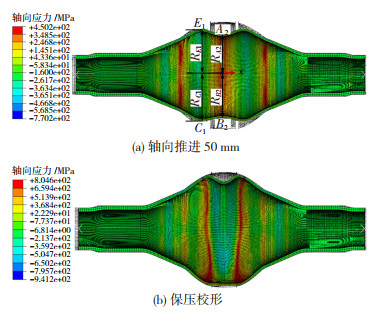
2.3.2 加载路径Ⅱ下模拟结果及分析壁厚偏差ω=0.5 mm的阶梯管参照加载路径Ⅱ在左、右滑动模推进至20 mm时,轴向应力为压应力,胀形区缓慢平直胀起;随着左、右滑动模的推进,压应力σρ数值逐渐增大,胀形区两侧先于中部胀形,呈双鼓形(见图 8(a)),中间储料增多;随着胀形的进行,由于内压过小,轴向压应力过大,中间储料过多,增压校形后,薄壁侧未贴模,厚壁侧形成褶皱,如图 8(b)所示。加载路径Ⅱ下不同ω管坯模拟结果见表 2。
|
图 8 加载路径Ⅱ下ω=0.5 mm时模拟结果 Fig.8 Simulation results of tube blanks with ω=0.5 mm at loading path Ⅱ: (a) axial propulsion 50 mm; (b) pressure maintaining sizing |
| 表 2 加载路径Ⅱ下不同ω管坯推进50 mm时模拟结果 Table 2 Simulation results of tube blanks with different ω when pushed 50 mm at loading path Ⅱ |
加载路径Ⅱ模拟结果表明:1)壁厚偏差ω越大,厚壁侧双鼓形越突出,与薄壁侧变形差异越小。当ω由0.2 mm增至0.8 mm,厚壁侧的半径RE1由199.6 mm减至198.5 mm,RA2由181.8 mm减至178.1 mm;薄壁侧的半径RC1由200.3 mm增至202.1 mm,RB2由185.5 mm增至193.4 mm;2) ω越大,厚壁侧两侧与中部之间落差Δ越大,中部储料越多,越容易形成褶皱。当ω由0.2 mm增至0.8 mm,厚壁侧Δ由17.8 mm增至20.4 mm。
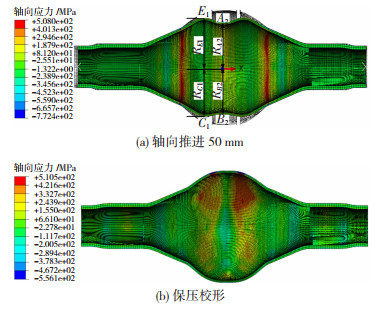
2.3.3 加载路径Ⅲ下模拟结果及分析与加载路径Ⅱ相比,壁厚偏差ω=0.5 mm的阶梯管参照加载路径Ⅲ在轴向推进34 mm后,胀形区轴向压应力σρ数值开始减小,两侧与中部的变形差异变小,中部变形逐渐赶上两侧;当滑动模具推进至50 mm时,薄壁侧轴向压应力σρ数值已趋近于0,并有向拉应力转化的趋势(见图 9(a)),随着胀形的进行,中部在拉应力作用下变形超过两侧;增压校形后,得到外形饱满、减薄率合适的的预成形管坯,如图 9(b)所示。加载路径Ⅲ下不同ω管坯模拟结果见表 3。
|
图 9 加载路径Ⅲ下ω=0.5 mm时模拟结果 Fig.9 Simulation results of tube blanks with ω=0.5 mm at loading path Ⅲ: (a) axial propulsion 50 mm; (b) pressure maintaining sizing |
| 表 3 加载路径Ⅲ下不同ω管坯推进50 mm时模拟结果 Table 3 Simulation results of tube blanks whe different ω when pushed 50 mm at loading path Ⅲ |
加载路径Ⅲ模拟结果表明:1)薄壁侧、厚壁侧变形差异增大,胀形区两侧胀形减慢,中部胀形加快,二者之间落差减小;壁厚偏差ω越大,薄壁侧、厚壁侧变形差异越大,胀形区两侧与中部之间落差越小。当ω由0.2 mm增至0.8 mm,厚壁侧的半径RE1由200.5 mm减至199.0 mm、RA2由184.9 mm减至180.7 mm,落差Δ由15.6 mm增至18.3 mm;薄壁侧的半径RC1由201.5 mm增至204.2 mm、RB2由190.2 mm增至201.0 mm; 2)校形保压后,壁厚偏差ω为0.2、0.5和0.8mm的管坯,薄壁侧最大减薄率分别为16.8%、17.0%、17.8%,厚壁侧最大减薄率分别为13.8%,13.2%,13.3%,均满足胀压成形工艺设计要求。
由以上所有模拟结果可知,对于壁厚偏差管坯的液压胀形,按照内压先升高后降低再升高(即轴向压应力先增大后减小)的路径进行加载,既可实现轴向补料,又能实现管坯胀形,从而得到符合工艺要求的管件。
3 液压胀形试验 3.1 胀形模具某重型卡车桥壳预成形管坯的液压胀形试验在THP63-800/1250×2型液压机上进行,液压胀形模具见图 10。

|
图 10 液压胀形模具 Fig.10 Hydroforming die 1—主滑块;2—上模座;3—左滑块;4—左滑动模;5—下模座;6—下固定模;7—上固定模;8—右滑动模;9—右滑块 1—upper slider; 2—upper die seat; 3—left slider; 4-left sliding die; 5—lower die seat; 6—lower clamping die; 7—upper clamping die; 8—right sliding die; 9—right slider. |
左滑动模4、右滑动模8分别固定于左滑块3、右滑块9上;上固定模7、下固定模6分别固定于上模座2、下模座5上,上模座与液压机主滑块1相连,下模座固定于液压机工作平台上。
3.2 阶梯管坯按图 4所示的工艺选取3根壁厚偏差相近但平均壁厚不同的初始管坯,编号分别为001、002、003,按相同方法取截面Ⅰ距左端448 mm、截面Ⅳ距右端438 mm的中间部分,从中间向外选取4个横截面分别按145 mm等间距的测量所选点的壁厚(见表 4),平均壁厚分别为9.80、9.88和9.84 mm,周向最大壁厚偏差依次为0.49、0.50和0.52 mm(最大壁厚偏差分别为平均壁厚的5.00%,5.06%,5.28%)。
| 表 4 初始管坯壁厚 Table 4 Thickness of initial tube blank |
首先对3根初始管坯进行缩径,再对其进行退火处理后得到图 11所示阶梯管坯,然后在如图 10所示的专用液压机上进行液压胀形试验。

|
图 11 阶梯管坯 Fig.11 Stepped tube blank |
编号001、002、003的管坯加载路径分别对应图 6中的Ⅰ、Ⅱ、Ⅲ。编号001管坯参照加载路径Ⅰ在左、右滑模推进至50 mm时,薄壁侧沿轴向发生开裂,如图 12(a)所示,薄壁侧呈中部高于两侧的单鼓形,厚壁侧呈两侧略高于中部的双鼓形,经测量裂口最高点至中心的距离为223.5 mm,胀形系数为1.49,裂口处最薄壁厚为7.35 mm,减薄率为平均壁厚的25%。

|
图 12 胀形管坯 Fig.12 Bulging tube blank: (a) 001; (b) 002; (c) 003 |
图 12(b)为编号002的管坯参照加载路径Ⅱ胀形后的管坯,由于后期型腔内充液较少,内压较低,保压校形后,胀形区中部低于两侧,未贴模,形成褶皱。经测量,薄壁侧两侧最大半径为206 mm,中部最小半径为198.9mm;厚壁侧两侧最大半径为203 mm,中部最小半径为191.1 mm。
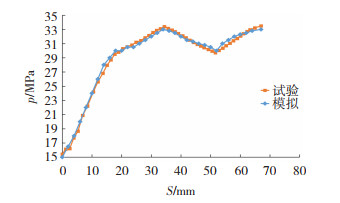
图 12(c)为编号003管坯参照加载路径Ⅲ进行胀形后的样件,图 13中可以看出试验与模拟的加载曲线基本一致,后期补液升压时试验值略微低于模拟值,结合加载路径Ⅱ胀形结果可以得知,在左、右滑动模具进给一半后缓慢降低内压,随后增大补液量(即增大内压)能够减少胀形区中部的储料,促动中部的变形,最终获得轮廓清晰、外形饱满、无缺陷的管件。
|
图 13 加载路径Ⅲ下内压-轴向推进量关系曲线 Fig.13 Simulated and experimental pressure-shift curves at loading mode Ⅲ |
利用超声波测厚仪测量胀形后管坯的壁厚,以管坯中间截面为作为起始点,沿轴线方向向两侧每隔15 mm测量一次壁厚,记录数据并与模拟值进行对比,如图 14所示。

|
图 14 003试验样件胀形区壁厚分布 Fig.14 Wall thickness distribution in bulging zone of 003 test sample: (a) the thin-wall side; (b) the thick-wall side |
从图 14(a)可以看出,试验与模拟壁厚分布大体趋势相同,仿真结果对应的薄壁侧最高点壁厚为8.09 mm,壁厚减薄率为16.96%;试验测量薄壁侧最高点壁厚为7.99 mm,减薄率为平均壁厚的18.80%,仿真值与试验值相差1.84%。
由图 14(b)可以看出,仿真结果对应的厚壁侧最高点壁厚为8.88 mm,减薄率为13.33%;试验测量厚壁侧最高点壁厚为8.67 mm,减薄率为平均壁厚的11.89%,仿真值与试验值相差1.44%。
经测量,胀形区中间截面最大外径为465.3 mm,比最大径向设计尺寸466 mm小了0.15%,满足工艺设计要求。
4 结论1) 建立了带壁厚偏差的管坯液压胀形的力学模型,揭示了不同轴向应力状态下壁厚偏差对管坯成形的影响规律,并给出了带壁厚偏差管坯液压胀形的加载路径设计标准:轴向应力为压应力时,有助于金属流动储料,但储料过多易失稳起皱,故在轴向压应力增大至一定值后需同时增大液体内压以减少轴向补料,从而得到符合要求的管坯。
2) 预成形管坯液压胀形有限元模拟结果表明:在加载路径Ⅰ下,3种管坯薄壁侧均在合模前发生开裂且壁厚偏差由0.2 mm增至0.8 mm,薄壁侧极限胀形系数由1.51减至1.47;加载路径Ⅱ下,3种管坯厚壁侧均失稳形成褶皱且壁厚偏差由0.2 mm增至0.8 mm,薄壁侧中部极限胀形系数由1.24增至1.29;加载路径Ⅲ下,3种管坯均成形良好,符合工艺要求。
3) 基于理论分析及有限元模拟,给出了适用于带壁厚偏差管坯液压胀形的最优加载路径:前期内压先升高后降低使管坯在胀形的同时轴向应力为压应力,以实现轴向补料,从而弱化壁厚偏差的影响;后期内压再升高,可避免胀形区因补料过多失稳形成褶皱,进而得到符合工艺要求的管坯。
4) 桥壳实际液压胀形结果表明:在加载路径Ⅰ下,管坯薄壁侧在模具工进50 mm时发生开裂;在加载路径Ⅱ下,管坯胀形区在保压校形后形成死皱;在加载路径Ⅲ下,管坯成形性好,符合工艺要求,验证了理论分析与有限元模拟的正确性。
| [1] |
HARTL C. Research and advances in fundamentals and industrial applications of hydroforming[J]. Journal of Material Processing Technology, 2005, 167(2-3): 382-392. DOI:10.1016/j.jmatprotec.2005.06.035 |
| [2] |
崔令江, 王刚, 王宏伟, 等. AZ80镁合金板材快速气压胀形工艺研究[J]. 材料科学与工艺, 2015, 23(3): 81-84. CUI Lingjiang, WANG Gang, WANG Hongwei, et al. Research on quick gas blow forming technology for AZ80 magnesium alloy sheet[J]. Materials Science and Technology, 2015, 23(3): 81-84. DOI:10.11951/j.issn.1005-0299.20150316 |
| [3] |
蔡宣明, 张伟, 范志强, 等. 汽车后桥壳胀形工艺加载路径研究[J]. 车辆与动力技术, 2018(4): 1-5. CAI Xuanming, Zhang Wei, FAN Zhiqiang, et al. Study on the loading path of automobile rear axle housing bulging technology[J]. Vehicle & Power Technology, 2018(4): 1-5. DOI:10.16599/j.cnki.1009-4687.2018.04.001 |
| [4] |
AYDEMIR A, VREE J H P D, BREKELMANS W A M, et al. An daptive simulation approach designed for tube hydroforming processes[J]. Journal of Materials Processing Technology, 2005, 159(3): 303-310. DOI:10.1016/j.jmatprotec.2004.05.018 |
| [5] |
吴娜, 王连东, 王晓迪, 等. 基于均匀增容的大变径比管件液压胀形加载路径研究[J]. 锻压技术, 2019(5): 86-92. WU Na, WANG Liandong, WANG Xiaodi, et al. Research on hydroforming loading path of tube with large diameter ratio based on uniform capacity change[J]. Forging & Stamping technology, 2019(5): 86-92. DOI:10.13330/j.issn.1000-3940.2019.05.015 |
| [6] |
CARLEER B, KEVIE G V D, WINTER L D, et al. Analysis of the effect of material properties on the hydroforming process of tubes[J]. Journal of Materials Processing Technology, 2000, 104(1-2): 158-166. DOI:10.1016/S0924-0136(00)00530-6 |
| [7] |
张庆, 周磊, 赵长财. 薄壁管胀形成形极限分析及其数值模拟[J]. 机械工程学报, 2004(03): 137-139. ZHANG Qing, ZHOU Lei, ZHANG Changcai. Limit analysis and numerical simulation of thin wall tube bulging[J]. Chinese Journal of Mechanical engineering, 2004(03): 137-139. DOI:10.3321/j.issn:0577-6686.2004.03.028 |
| [8] |
王连东, 程文冬, 梁辰, 等. 汽车桥壳液压胀形极限成形系数及胀裂判据[J]. 机械工程学报, 2007, 43(5): 210-213. WANG Liandong, CHENG Wen dong, LIANG Chen, et al. Forming limit coefficient and bursting criterion of hydroforming automobile axle housings[J]. Chinese Journal of Mechanical engineering, 2007, 43(5): 210-213. DOI:10.3321/j.issn:0577-6686.2007.05.036 |
| [9] |
SHIRAYORI A, FUCHIZAWA S, NARAZAKI M. Deformation behavior of tubes with thickness deviation in circumferential direction during hydraulic free bulging[J]. Journal of Materials Processing Technology, 2003, 139: 58-63. DOI:10.1016/S0924-0136(03)00182-1 |
| [10] |
SHIRAYORA A, FUCHIZAWA S, NARAZAKI M. Influence of initial thickness deviation on tube deformation during free hydraulic bulging[J]. Journal of the JSTP, 2003, 44: 378-381. |
| [11] |
YANG Lianfa, GUO Cheng, DENG Yang. Deformation behavior of A6063 tube with initial thickness deviation in free hydraulic bulging[J]. Transactions of Nonferrous Metals Society of China, 2006, 16(S3): 1392-1396. |
| [12] |
HE Zhubin, WANG Zhibiao, LIN Yanli, et al. A modified Marciniak-Kuczynski model for determining the forming limit of thin-walled tube extruded with initial eccentricity[J]. International Journal of Mechanical Sciences, 2018, 20: 715-723. DOI:10.1016/j.ijmecsci.2018.12.029 |
| [13] |
王连东, 梁晨, 马雷, 等. 汽车桥壳液压胀形工艺的研究及最新进展[J]. 燕山大学学报, 2012, 36(3): 206-209. WANG Liandong, LIANG Chen, MA Lei, et al. Research and latest development of hydroforming process for automobile axle housing[J]. Journal of Yanshan University, 2012, 36(3): 206-209. DOI:10.3969/j.issn.1007-791X.2012.03.004 |
| [14] |
王连东, 庞蒙, 周立凤, 等. 中型卡车胀压成形桥壳预成形管坯的设计及成形分析[J]. 中国机械工程, 2015, 12(26): 1684-1689. WANG LIandong, PANG Meng, ZHOU Lifeng, et al. Preforming tube's design and deformation analysis of medium-sized truck bulging-pressing axle housing[J]. China Mechanical Engineering, 2015, 12(26): 1684-1689. DOI:10.3969/j.issn.1004-132X.2015.12.022 |
| [15] |
刘超, 王连东, 刘恒, 等. 带壁厚偏差的无缝钢管推压-拉拔复合缩径[J]. 中国机械工程, 2018, 29(11): 1375-1379. LIU Chao, WANG Liandong, LIU Heng, et al. Seamless steel tube with wall thickness deviation in pushing-pulling necking[J]. China Mechanical Engineering, 2018, 29(11): 1375-1379. DOI:10.3969/j.issn.1004-132X.2018.11.019 |
 2021, Vol. 29
2021, Vol. 29


