2. 内蒙古自治区先进制造技术重点实验室,呼和浩特 010051
2. Inner Mongolia Key Laboratory of Advanced Manufacturing Technology, Hohhot 010051, China
12CrNi3合金钢具有良好的力学性能,被广泛应用在飞机、船舶、汽车等重要机械零部件的制造中,与15Cr、20Cr钢相比,其强度、塑性、淬透性较高,因而12CrNi3合金钢常用来制作表面耐磨、热处理变形小的轴、杆和有冲击载荷下工作的各种传动齿轮、凸轮轴等。为了提高12CrNi3合金钢的疲劳强度、耐磨性,以及延长使用寿命,通常采用调质[1-3]、氮化[4-5]、渗碳[6-9]等表面处理工艺,其中渗碳是比较实用和广泛的一种表面强化工艺。12CrNi3合金钢经过渗碳处理后,表面可以获得较高的硬度,使其具有“外强内韧”的特点,从而延长使用寿命。然而,高周次工况下渗碳12CrNi3合金钢失效问题频频发生,为了更好地把握渗碳12CrNi3合金钢疲劳失效规律,对渗碳12CrNi3合金钢在高周疲劳下的疲劳特性及疲劳强度预测方法进行研究具有重要意义。
随着现代工业的不断发展,一些高精尖领域对合金钢的强度、可靠性和力学性能要求越来越苛刻,因此对合金钢的寿命及疲劳强度的研究受到越来越多学者的关注,并由此提出了一系列疲劳强度预测模型。孙振铎等[10]基于极值分布函数,构建了一种考虑夹杂尺寸的疲劳强度预测模型;丁明超等[11]考虑微观划痕的影响,提出了一种具有精度优势的疲劳强度预测方法;段红燕等[12]考虑了真实应力应变曲线,提出了一种新型的疲劳强度预测模型;彭艳等[13]基于连续介质损伤力学,构建了一种考虑平均剪应力效应的纯扭疲劳强度预测模型;高婧等[14]基于STW模型,提出了服从威布尔分布的疲劳强度预测方法。然而基于威布尔分布[15],考虑应力和疲劳寿命关系的疲劳强度预测模型尚鲜有研究报道,同时许多疲劳强度预测模型的预测结果不够准确。因此,亟需建立一种安全可靠的高周疲劳强度预测方法。
本文在应力比为-1的条件下, 对渗碳12CrNi3合金钢开展高周疲劳实验。基于威布尔分布,建立了失效概率为1%时的渗碳12CrNi3合金钢高周疲劳强度预测模型。通过均方误差(MSE)对强度预测模型进行修正,将12CrNi3合金钢疲劳寿命P-S-N曲线与修正后疲劳强度模型99%MSE下界线进行对比分析,以期为以渗碳12CrNi3合金钢为材料进行构件的可靠性设计提供更为安全的下界。
1 实验 1.1 材料与试样本文中疲劳实验选用的材料为12CrNi3合金钢,其化学成分如表 1所示。首先将圆棒形原料加工成沙漏状,然后沿其轴线方向用360~2 000目砂纸打磨,最终试样长度为152 mm,最小横截面积的直径为4.5 mm,圆弧表面粗糙度为0.32,试样几何尺寸如图 1所示。为使12CrNi3合金钢具有较高的硬度、耐磨性和疲劳强度,首先对其进行渗碳处理。渗碳后,12CrNi3合金钢材料表面层的含碳量提高,而表面的强度和硬度等指标仍达不到技术要求,因此在渗碳处理后的12CrNi3合金钢需进行淬火和低温回火的工序。具体工艺为:将渗碳处理后的12CrNi3合金钢在840 ℃的真空下油淬45 min,然后在160 ℃的空气下进行90 min的低温回火热处理。
| 表 1 12CrNi3合金钢的化学成分(质量分数/%) Table 1 Chemical composition of 12CrNi3 alloy steel (wt. %) |

|
图 1 试样的类型和尺寸(单位:mm) Fig.1 Type and dimensions of specimen |
在试样的最小截面处截取部分组织镶嵌为金相试样,然后通过砂纸打磨和抛光,再用4%的乙醇硝酸溶液进行侵蚀,最后使用扫描电子显微镜(JSM-6610LV,瑞盛科技有限公司)观测,金相试样的渗碳层和基体的微观组织形貌如图 2所示。

|
图 2 渗碳12CrNi3合金钢的微观组织 Fig.2 Microstructure of carburized 12CrNi3 alloy steel: (a)Microstructure of carburized layer; (b)Microstructure of the matrix region |
由图 2可以看到,在渗碳12CrNi3合金钢的渗碳层微观组织中,主要存在的是奥氏体和针状马氏体,而基体中的微观组织主要为板条马氏体。此外,在渗碳层和基体中的微观组织均存在非金属夹杂。
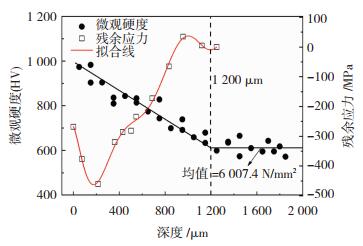
采用纳米压痕硬度测量仪(Nano-Indenter-G200,上海纳腾仪器有限公司),从试样的自由表面向内部每隔100 μm的距离进行硬度测量,最终测得试样的维氏硬度分布如图 3中黑色圆点所示。由图 3可知,随着测量深度的增加,试样的维氏硬度逐渐降低,当测量的深度超过1 200 μm时,试样的硬度达到稳定,约为6 007.4 N/mm2。导致该现象的原因主要是随着深度的加深,渗碳工艺的影响逐渐减小。当深度达到1 200 μm时影响消失,试样维氏硬度值趋于稳定。
|
图 3 微观硬度和残余应力与深度的关系 Fig.3 Relationship between micro-hardness, residual stress, and depth |
基于MTS 809材料测试系统(美特斯工业系统(中国)有限公司),分别对渗碳12CrNi3合金钢的5根相同疲劳试样进行单轴的力学拉伸性能测试,最终测得材料的弹性模量(Eh)为209 GPa,泊松比(νh)为0.3,屈服和抗拉强度分别为1 490和1 780 MPa。同时,基于TEC 4000 X射线衍射系统(美国TEC公司),可获得渗碳12CrNi3合金钢从表面到内部的残余应力值,如图 3中空心方块所示。由图 3可知,试样表面的残余应力为-268 MPa。当距离表面深度为214 μm时,残余压应力值最大,约为460 MPa。当距离表面深度达到1 100 μm时,残余应力大于零,最大残余应力为35 MPa。随着距离表面深度的继续增加,残余应力不断减小,当距离表面深度约为1 200 μm时,残余应力变为零,出现该现象的原因是:在试样渗碳层与心部基体的过渡区内,试样渗碳层内的残余应力与心部基体内的残余应力互为反作用力,从而使得试样径向内部的应力处于平衡。
1.3 实验方法在室温下,利用高频疲劳测试机(QBG-100,长春仟邦测试设备有限公司)对试样进行轴向加载的高周疲劳实验,实验频率为100 Hz,施加的应力比为-1,所施加的应力幅值为600~1 100 MPa。将试样分为6组,每组以100 MPa为间隔进行实验,当试样完全断裂或循环次数超过108次时终止实验,分别记录渗碳12CrNi3合金钢在不同应力幅值下的疲劳寿命数据。
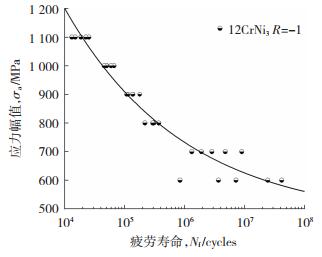
1.4 S-N曲线基于渗碳12CrNi3合金钢高周疲劳实验,结合Basquin公式,拟合得到其应力-寿命曲线如图 4所示。由图 4可知,在高应力区疲劳数据点分布较为集中,而在低应力区疲劳数据点分布较为分散。随着疲劳寿命的增加,渗碳12CrNi3合金钢的疲劳强度呈现递减的趋势。此外,所有的疲劳寿命都在108循环周次内结束,未出现传统的疲劳极限。
|
图 4 渗碳12CrNi3合金钢的S-N曲线 Fig.4 S-N curve of carburized 12CrNi3 alloy steel |
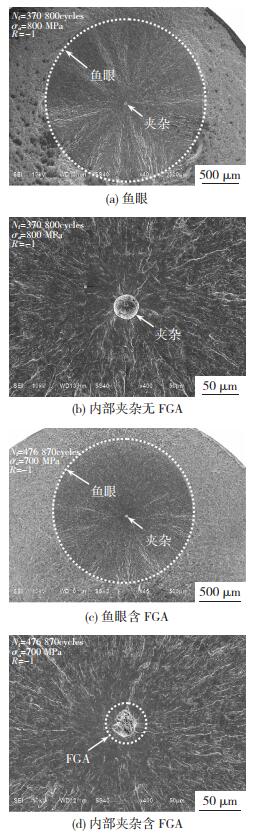
基于扫描电镜,可以观察到试样疲劳失效的典型断口,结果如图 5所示。在图 5(a)和(c)中,可以观测到疲劳破坏的典型特征——鱼眼,并发现所有试样的疲劳失效都源于内部夹杂。当疲劳寿命低于5×105循环周次时,夹杂周围不存在细晶粒区,如图 5(b)所示。而当疲劳寿命高于1×106循环周次时,在夹杂周围可以观测到细晶粒区,如图 5(d)所示。其中,细晶粒区(Fine Granular Area,FGA)为存在于夹杂周围的一个奇特的粗糙裂纹区。由于夹杂与基体材料的弹性模型不同,在循环交变载荷的作用下,夹杂会改变其周围基体局部应力分布,进而导致裂纹萌生,形成细晶粒区。此外,在应力比为-1时,所有的裂纹源均位于试样的心部基体中,即使试样的渗碳层内存在更大的夹杂,也不会诱发试样的疲劳失效。这是因为渗碳层中的高硬度和残余压应力对渗碳层中夹杂产生的裂纹起到了抑制作用。
|
图 5 典型断口表面观测 Fig.5 Observation of typical fracture surfaces: (a)fisheye; (b)internal inclusion without FGA; (c)fisheye with FGA; (d)internal inclusion with FGA |
根据诱发裂纹萌生位置和断口形貌观测,可以将疲劳失效模式分为表面失效、内部无细晶粒区失效(图 5(a)和(b))和内部有细晶粒区失效(图 5(c)和(d))3种。对于内部失效,内部夹杂诱发裂纹,裂纹由试样内部萌生并向外扩展,随着所受应力的不断增加,裂纹继续向外扩展直至试样断裂。而对于外部失效而言,在外加载荷和表面残余应力的共同作用下,由于表面夹杂产生应力集中,导致裂纹产生并由表面不断向内部扩展直至试样断裂。在应力比为-1时,观测试样断口形貌,发现试样心部基体中存在非金属夹杂,且所有的裂纹源均位于心部基体中。因此,可以认为在应力比为-1时,疲劳裂纹的萌生是由于心部基体中非金属夹杂诱发导致。
2 疲劳强度预测模型构建 2.1 渗碳12CrNi3钢疲劳数据的参数估计基于实验得到的数据,发现渗碳12CrNi3合金钢疲劳数据服从威布尔分布。其中威布尔累计分布函数为
| $ F(t)=1-\exp \left[-\left(\frac{t-\gamma}{\beta}\right)^\alpha\right] $ | (1) |
式中:α为形状参数,决定威布尔分布函数曲线的基本形状;γ为最小寿命;β为尺度参数。
灰色估计法[16]具有迭代次数少、求解速度快的优点,因此,采用灰色估计法对威布尔分布的参数进行估计,结合渗碳12CrNi3合金钢的疲劳数据,得到其威布尔三参数如表 2所示。
| 表 2 渗碳12CrNi3合金钢疲劳寿命的W(α, β, γ) 参数估计 Table 2 W(α, β, γ) parameter estimation of fatigue life of carburized 12CrNi3 alloy steel |
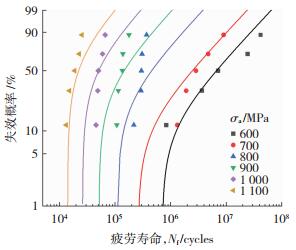
基于灰色估计法得到威布尔W(α, β, γ)三参数,将其带入式(1),得到渗碳12CrNi3合金钢在不同应力幅值下的失效概率曲线。如图 6所示,当应力幅值为600、700、900、1 000和1 100 MPa时,渗碳12CrNi3合金钢失效概率数据点均位于相对应的失效概率曲线附近;当应力幅值为800 MPa时,其失效概率曲线与失效概率数据点存在偏差。尽管有些失效概率曲线与失效概率数据点有所偏离,但总体上参数拟合效果很好。
|
图 6 渗碳12CrNi3合金钢的失效概率曲线 Fig.6 Failure probability curve of carburized 12CrNi3 alloy steel |
采用Coleman[17]阐述的模型基本函数形式,cdf基本函数为
| $ F(t \mid L)=1-\exp \left\{-\psi\left[\int_0^t \kappa(L(s)) \mathrm{d} s\right]\right\}\; t \geqslant 0 $ | (2) |
式中:ψ(x)为故障率函数;κ(x)为分解规则;L(t)为与时间有关的加载函数。
由于实验为恒幅载荷,所以用σa代替L(t)。使用威布尔故障率函数和幂律规则:
| $ \psi_W(x)=x^\alpha, x \geqslant 0 $ | (3) |
| $ \kappa_p(x)=\beta x^\rho $ | (4) |
将式(3)和式(4)代入公式(2)中,化简可得
| $ F\left(t \mid L_0\right)=1-\exp \left\{-\left[\beta\left(\sigma_{\mathrm{a}}\right)^\rho\left(t-t_0\right)\right]^\alpha\right\} \quad t \geqslant t_0 $ | (5) |
式(2)的积分下限由0变为t0时,重新整理为
| $ F\left(t \mid L_0\right)=1-\exp \left\{-\left[\frac{t-t_0}{\beta_*}\right]^\alpha\right\}\quad t \geqslant t_0 $ | (6) |
其中β*=β-1(σa)-ρ。
将式(6)中t0替代为γ(σa),此时式(6)中t0,β*成为与负载σa相关的参数,其值受应力幅值σa的影响。此时需要估计的参数为α、β、γ和ρ。
基于灰色估计法得到的W(α, β, γ)参数,取α的均值,即α=0.8。
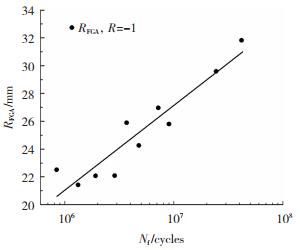
由于疲劳裂纹所形成的区域可近似为圆形,故使用扫描电子显微镜SEM及图形处理软件Image J可以测得疲劳断口处细晶粒区域面积的半径RFGA。在应力比R为-1时,疲劳断口处细晶粒区域面积的半径RFGA与疲劳寿命之间的关系如图 7所示。由图 7可以看到,RFGA尺寸随着疲劳寿命Nf的增加呈增长趋势,由此可知,疲劳寿命越长,细晶粒区的面积越大。此外,FGA的形成消耗了90%以上的疲劳寿命。因此,RFGA尺寸是预测疲劳强度的一个重要参数。基于本研究团队前期对疲劳累积损伤所造成的不同RFGA尺寸的研究,已构建的累积损伤理论的疲劳强度预测模型[18]为
|
图 7 RFGA与疲劳寿命Nf之间关系 Fig.7 Relationship between RFGA and fatigue life Nf |
| $ \sigma_{\mathrm{a}}=\frac{(1-R)}{2}\left(\frac{m \sigma_{\mathrm{b}}}{\log N_{\mathrm{f}}-m \log \log \frac{R_{\mathrm{FGA}}}{R_{\mathrm{inc}}}-n}-\sigma_{\mathrm{r}}\right) $ | (7) |
式中:σb为抗拉强度, 为1 780 MPa;σr为残余应力;m,n为拟合参数, 分别为1.95和3.1。
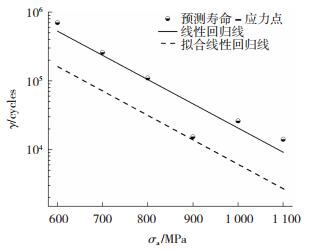
基于累积损伤理论的疲劳强度预测模型,可以得到不同疲劳寿命下渗碳12CrNi3合金钢的疲劳强度,如图 8黑色半圆点所示。根据预测所得寿命-应力拟合得到其线性回归线。由于γ为威布尔函数中最小寿命,其值必须小于所有疲劳寿命,因此拟合的γ(σa)函数如图 8虚线所示。使用Basquin公式来表示拟合的γ(σa)函数,
|
图 8 γ(σa)的拟合线性回归线 Fig.8 Fitting linear regression line of γ(σa) |
| $ \hat{\gamma}(x)=\frac{1}{2}\left(\frac{x}{a}\right)^{\frac{1}{b}} 600\; \mathrm{MPa} \leqslant x \leqslant 1\,100\; \mathrm{MPa} $ | (8) |
其中, a=5 383.8,b=-0.155。
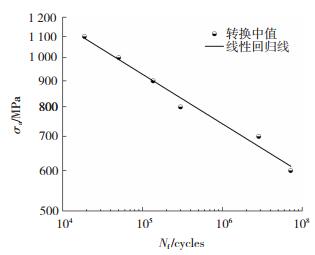
取每个应力幅值下寿命数据的中位数作为转换中值,其线性回归线如图 9所示。参数ρ由图中线性回归线进行估计,其斜率为-1/ρ,可得ρ的估计值为3.82。将σa=900 MPa时的转换中值带入式(6),求得剩余参数
|
图 9 12CrNi3合金钢疲劳数据的线性回归线 Fig.9 Linear regression line for fatigue data of 12CrNi3 alloy steel |
将上述的参数α、β、a、b和ρ代入式(6)可以得到渗碳12CrNi3合金钢的疲劳强度预测模型,即
| $ \begin{aligned} F\left(t / L_0\right)= & 1-\exp \left\{-\left[5.292 \times 10^{-17}\left(\sigma_{\mathrm{a}}\right)^{3.82}[t-\right.\right. \\ & \left.\left.\left.\frac{1}{2}\left(\frac{\sigma_{\mathrm{a}}}{5\,383.8}\right)^{-\frac{1}{0.155}}\right]\right]^{0.8}\right\} \end{aligned} $ | (9) |
式中:t为疲劳寿命;σa为应力幅值。
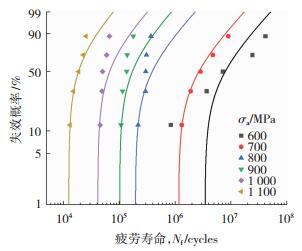
基于构建的疲劳强度预测模型,得到渗碳12CrNi3合金钢在不同应力下的失效概率曲线,如图 10所示,可以看到,在相同应力幅值下,渗碳12CrNi3合金钢的失效概率曲线与失效概率数据点基本相吻合。
|
图 10 基于疲劳强度模型的失效概率曲线 Fig.10 Failure probability curve based on fatigue strength model |
基于公式(9),当失效概率为1%时,可以得到渗碳12CrNi3合金钢的疲劳强度预测曲线,如图 11所示。其中,大部分疲劳寿命数据点位于疲劳强度预测曲线之上,但仍有少数疲劳寿命点位于疲劳强度预测曲线之下。

|
图 11 渗碳12CrNi3合金钢疲劳强度预测曲线 Fig.11 Prediction curve of fatigue strength of carburized 12CrNi3 alloy steel |
综上所述,构建的失效概率为1%时的疲劳强度预测模型可以用来预测渗碳12CrNi3合金钢的疲劳强度,但从预测疲劳强度安全可靠性角度,仍需对模型进一步讨论。因此需要对构建的疲劳强度预测模型进一步修正。
3 基于均方误差的疲劳强度修正模型 3.1 传统的P-S-N曲线在实际工程应用中,尤其在构件的可靠性设计时,常需要不同存活率下的S-N曲线,即P-S-N曲线。本文选择应力水平进行成组试验,得到每个应力水平的疲劳寿命分布的数字特征,然后将各应力幅值下疲劳寿命分布曲线上可靠度相等的点用曲线连接起来,得到给定可靠度的一组S-N曲线,即P-S-N曲线。P-S-N曲线试验数据处理如下。
(a) 将相同应力幅值下测得的疲劳寿命从大到小排列,并取相应对数列表。
(b) 计算其破坏率和存活率。计算公式如下:
| $ P_i=i /(N+1) $ | (10) |
| $ P_s=1-P_i $ | (11) |
式中:Pi为破坏率;Ps为存活率;N为寿命。
(c) 对x=lgN进行正态验证,对每组应力幅值下的对数疲劳寿命xp和正态偏量进行回归估计拟合,并求得存活率分别为1%、10%、50%、90%和99%的回归方程。
| $ x_{\mathrm{p}}=\mu+u_{\mathrm{p}} s $ | (12) |
式中:μ为均值;s为标准差;up为与破坏率Pi对应的标准正态偏量,查表可得[19]。
(d) 根据不同存活率下的回归方程,利用最小二乘法可以拟合得到不同存活率下的P-S-N曲线。
通过上述步骤,能够得到渗碳12CrNi3合金钢不同存活率下的P-S-N曲线。
3.2 99%MSE下界线疲劳强度模型构建从预测疲劳强度安全可靠性角度,仍需对模型进一步讨论。因而采用均方误差(MSE)[20-22]方法对模型进一步修正。均方误差是反映预测数据与真实值之间差异程度的一种度量,它可以评价数据的变化程度。MSE是预测值与实际值差值的平方和的平均数,如式(13)所示。
| $ \begin{aligned} \text { MSE }= & \frac{1}{n} \sum\limits_{i=1}^n e_i^2=\frac{1}{n} \sum\limits_{i=1}^n\left(y_i-\dot{y}\right)^2=\frac{1}{n}\left[\left(y_1-\dot{y}\right)^2+\right. \\ & \left.\left(y_2-\dot{y}\right)^2+\cdots+\left(y_n-\dot{y}\right)^2\right] \end{aligned} $ | (13) |
式中:误差ei为模型预测值和实验数据之间的差值;yi为相同应力下的实验寿命;
置信区间是一种常用的区间估计方法,分别以统计量的置信上限和置信下限为上下界构成的区间。疲劳寿命数据的显著水平α为0.01,则置信度为99%。置信区间的计算方法为
| $ \operatorname{Pr}\left(|Z|=\left|\frac{\dot{y}-y_i}{\sqrt{\omega^2 / n}}\right| \leqslant Z_{\frac{\alpha}{2}}\right)=1-\alpha=0.99 $ | (14) |
| $ \operatorname{Pr}\left(-Z_{\frac{\alpha}{2}} \leqslant \frac{\dot{y}-y_i}{\sqrt{\omega^2 / n}} \leqslant Z_{\frac{\alpha}{2}}\right)=99 \% $ | (15) |
化简得
| $ \operatorname{Pr}\left(\dot{y}-\frac{\omega}{\sqrt{n}} Z_{\frac{\alpha}{2}} \leqslant y_i \leqslant \dot{y}+\frac{\omega}{\sqrt{n}} Z_{\frac{\alpha}{2}}\right)=99 \% $ | (16) |
式中:ω为寿命的均方误差,即ω=MSE;查表得[23]随机变量Z0.005=2.58。
因此,置信度99%的置信区间为[
当置信度为99%时,将同一应力下的5个实验寿命和模型预测寿命代入式(16)可求得其置信区间。不同应力幅值下置信区间的下限,构成了模型99%MSE下界线。
3.3 疲劳强度预测结果比较渗碳12CrNi3合金钢的P-S-N曲线和99%MSE下界线如图 12所示。由图 12可以看到,疲劳寿命数据基本都位于1%存活率和99%存活率的P-S-N曲线之间,但在应力幅值为600 MPa时,有一个数据点位于1%存活率的P-S-N曲线之外。因此,在构件的可靠性设计时,当以其1%存活率的P-S-N曲线作为下界参考是不够安全的。而当应力幅值为600和700 MPa时,尽管实验所得疲劳数据存在较大的分散性,但99%MSE下界线仍能将所有的疲劳数据包含其中,因此,在加载方式为拉压条件下的构件可靠性设计时,以99%MSE下界线作为12CrNi3合金钢疲劳数据的下界是安全的。

|
图 12 疲劳寿命数据的P-S-N曲线和99%MSE下界线 Fig.12 P-S-N curve and 99%MSE lower boundary of fatigue life data |
综上所述,渗碳12CrNi3合金钢的部分疲劳寿命数据点位于1%存活率的P-S-N曲线之外,而模型的99%MSE下界线将全部疲劳寿命数据点包含其中。对比渗碳12CrNi3合金钢1%存活率的P-S-N曲线,模型的99%MSE下界线可以更安全地作为渗碳12CrNi3合金钢疲劳数据的下界,且曲线具有较安全的预测精度。
4 结论基于本文渗碳12CrNi3合金钢的疲劳实验数据及相关分析,得到的主要结论如下。
1) 在应力比为-1下,对渗碳12CrNi3合金钢开展高周疲劳实验,构建了渗碳12CrNi3合金钢疲劳寿命的S-N曲线。
2) 基于威布尔分布,结合应力和疲劳寿命关系,建立了失效概率为1%下的渗碳12CrNi3合金钢高周疲劳强度预测模型。结果表明,大部分疲劳寿命数据点位于疲劳强度预测曲线之上,只有少数疲劳寿命点位于疲劳强度预测曲线之下。因此,构建的失效概率为1%时的疲劳强度预测模型具有较安全的预测精度。
3) 基于均方误差(MSE)方法,修正疲劳强度预测模型。将得到的99% MSE下界线与P-S-N曲线中P=1%的S-N曲线对比,发现12CrNi3合金钢疲劳寿命数据点均位于模型99% MSE下界线内,表明在以渗碳12CrNi3合金钢为材料,加载方式为拉压条件下的实际工程中,修正后模型99% MSE下界线可以更安全地作为构件可靠性设计的下界。
需要注意的是,本文研究内容是针对于加载方式为拉压条件下,对于其是否适用于其他加载方式仍需进一步研究。
| [1] |
王进, 褚忠, 李君飞, 等. F35MnVN非调质钢高温本构模型对比研究[J]. 材料科学与工艺, 2012, 20(5): 143-148. WANG Jin, CHU Zhong, LI Junfei, et al. Comparative study on high temperature constitutive models of F35MnVN non-quenched steel[J]. Materials Science and Technology, 2012, 20(5): 143-148. |
| [2] |
余伟, 徐立善, 陈银莉, 等. 回火方式对调质高强度钢组织和性能的影响[J]. 材料科学与工艺, 2012, 20(1): 103-107. YU Wei, XU Lishan, CHEN Yinli, et al. Effect of tempering method on microstructure and properties of quenched and tempered high strength steel[J]. Materials Science and Technology, 2012, 20(1): 103-107. |
| [3] |
SOADY K A, MELLORB G, WESTG D, et al. Evaluating surface deformation and near surface strain hardening resulting from shot peening a tempered martensitic steel and application to low cycle fatigue[J]. International Journal of Fatigue, 2013, 54: 1-12. DOI:10.1016/j.ijfatigue.2013.03.019 |
| [4] |
张向峰, 龚代涛, 王均, 等. 不锈钢低温盐浴表面氮化技术发展与现状[J]. 材料科学与工艺, 2017, 25(6): 75-81. ZAHNG Xiangfeng, GONG Daitao, WANG Jun, et al. Development and status of nitriding technology on stainless steel surface in low temperature salt bath[J]. Materials Science and Technology, 2017, 25(6): 75-81. DOI:10.11951/j.issn.1005-0299.20160468 |
| [5] |
SHOICHI Kikuchi, SHO Yoshida, AKIRA Ueno. Improvement of fatigue properties of Ti-6Al-4V alloy under four-point bending by low temperature nitriding[J]. International Journal of Fatigue, 2019, 120: 1-7. DOI:10.1016/j.ijfatigue.2018.11.005 |
| [6] |
闫永明, 刘雅政, 周乐育, 等. 钎具钢23CrNi3Mo渗碳规律及显微组织研究[J]. 材料科学与工艺, 2013, 21(5): 102-108. YAN Yongming, LIU Yazheng, ZHOU Leyu, et al. Study on carburizing law and microstructure of 23CrNi3Mo brazing steel[J]. Materials Science and Technology, 2013, 21(5): 102-108. DOI: CNKI:SUN:CLKG.0.2013-05-017 |
| [7] |
龚敏, 黄健, 沈玉洁, 等. 预奥氏体化对中Mn TRIP钢组织及力学性能的影响[J]. 材料科学与工艺, 2014, 22(4): 6-11. GONG Min, HUANG Jian, SHEN Yujie, et al. Effect of preaustenitizing on microstructure and mechanical properties of Medium Mn TRIP steel[J]. Materials Science and Technology, 2014, 22(4): 6-11. DOI:10.11951/j.issn.1005-0299.20140402 |
| [8] |
NEHILA Abdelhak, LI Wei, GAO Ning, et al. Very high cycle fatigue of surface carburized CrNi steel at variable stress ratio: Failure analysis and life prediction[J]. International Journal of Fatigue, 2018, 111: 2-12. DOI:10.1016/j.ijfatigue.2018.02.006 |
| [9] |
SHIMAMURA Yoshinobu, NARITA Koichiro, ISHⅡ Hitoshi, et al. Fatigue properties of carburized alloy steel in very high cycle regime under torsional loading[J]. International Journal of Fatigue, 2014, 60: 4-6. DOI:10.1016/j.ijfatigue.2013.06.016 |
| [10] |
孙振铎, 侯东勃, 李志远. 渗碳Cr-Mn钢的夹杂分布特性及疲劳强度预测[J]. 兵器材料科学与工程, 2021, 44(1): 98-103. SUN Zhenduo, HOU Dongbo, LI Zhiyuan. Inclusion distribution characteristics and fatigue strength prediction of carburized Cr-Mn steel[J]. Ordnance Material Science and Engineering, 2021, 44(1): 98-103. DOI:10.14024/j.cnki.1004-244x.20201203.001 |
| [11] |
丁明超, 张元良, 咸宏伟, 等. 基于微观划痕的疲劳强度预测[J]. 东北大学学报, 2020, 41(5): 693-699. DING Mingchao, ZHANG Yuanliang, XIAN Hongwei, et al. Fatigue strength prediction based on micro scratches[J]. Journal of Northeastern University, 2020, 41(5): 693-699. DOI: CNKI:SUN:DBDX.0.2020-05-014 |
| [12] |
段红燕, 唐国鑫, 盛捷, 等. 一种新型的疲劳强度预测模型[J]. 上海交通大学学报, 2021, 51: 801-808. DUAN Hongyan, TANG Guoxin, SHEN Jie, et al. A new fatigue strength prediction model[J]. Journal of Shanghai Jiaotong University, 2021, 51: 801-808. DOI:10.16183/j.cnki.jsjtu.2021.051 |
| [13] |
彭艳, 李浩然, 刘洋. 考虑平均剪应力效应的纯扭疲劳强度预测[J]. 中国机械工程, 2020, 31(4): 396-402. PENG Yan, LI Haoran, LIU Yang. Prediction of pure torsional fatigue strength considering average shear stress effect[J]. China Mechanical Engineering, 2020, 31(4): 396-402. DOI:10.3969/j.issn.1004-132X.2020.04.00 |
| [14] |
高婧, 罗城. 基于SWT模型和威布尔分布的CFRP环带微动疲劳寿命预测[J]. 材料导报, 2021, 35(16): 16015. GAO Jing, LUO Cheng. Fretting fatigue life prediction of CFRP bands based on SWT model and Weibull distribution[J]. Material Review, 2021, 35(16): 16015. DOI: CNKI:SUN:CLDB.0.2021-16-003 |
| [15] |
BRUNO Pedrosa, MILAN Veljkovic, CARLOS A S, et al. Reliability of fatigue strength curves for riveted connections using normal and weibull distribution functions[J]. ASCE-ASME Journal of Risk and Uncertainty in Engineering Systems, Part A: Civil Engineering, 2020, 6(3): 25-39. DOI:10.3390/ma10091084 |
| [16] |
马契. 适用于风速的三参数威布尔分布的参数估计[D]. 北京: 华北电力大学, 2017. MA Qi. Parameter estimation of three-parameter Weibull distribution for wind speed[D]. Beijng: North China Electric Power University, 2017. |
| [17] |
COLEMAN B D. Time dependence of mechanical breakdown phenomena[J]. Journal of Applied Physics, 1957, 27(8): 862. DOI:10.1016/0043-1648(59)90025-0 |
| [18] |
郭扬, 邓海龙, 刘兵, 等. 渗碳12CrNi3合金钢疲劳寿命预测及变应力水平下残余寿命可靠性研究[J]. 制造技术与机床, 2021(12): 120-126. GUO Yang, DENG Hailong, LIU Bing, et al. Study on fatigue life prediction and residual life reliability of carburized 12CrNi3 alloy steel under variable stress level[J]. Manufacturing Technology and Machine Tools, 2021(12): 120-126. DOI:10.19287/j.cnki.1005-2402.2021.12.024 |
| [19] |
高镇同. 疲劳应用统计学[M]. 北京: 国防工业出版社, 1986.
|
| [20] |
HAN Ming. E-Bayesian estimations of parameter and its evaluation standard: E-MSE (expected mean square error) under different loss functions[J]. Communications in Statistics-Simulation and Computation, 2021, 50(7): 1971. DOI:10.1080/03610918.2019.1589510 |
| [21] |
YANG S, REN J, LI Z. Learning of neural networks based on weighted mean squares error function[C]// Second International Symposium on Computational Intelligence & Design. IEEE Computer Society, 2009: 241. DOI: 10.1109/iscid.2009.67
|
| [22] |
BEHESHTI S, HASHEMI M, SEJDIC E, et al. Mean square error estimation in thresholding[J]. IEEE Signal Processing Letters, 2010, 18(2): 103-106. DOI:10.1109/lsp.2010.2097590 |
| [23] |
李琼琳, 冉庆鹏. 正态总体方差最优置信区间的估计[J]. 佳木斯职业学院学报, 2017(4): 244-245, 247. LI Qionglin, RAN Qingpeng. Estimation of optimal confidence interval for variance of normal population[J]. Journal of Jiamusi Vocational College, 2017(4): 244-245, 247. DOI:10.3969/j.issn.1000-9795.2017.04.162 |
 2023, Vol. 31
2023, Vol. 31


