2. 辽宁工程技术大学 电气与控制工程学院,辽宁 葫芦岛 125000
2. Faculty of Electrical and Control Engineering, Liaoning Technical University, Huludao 125000, China
无损检测技术作为工业发展中不可缺少的有效工具,在一定程度上反映了一个国家工业的发展水平[1-2]。铝合金材料具有强度高、密度低、耐腐蚀性强等特性,广泛应用于航天设备、军工设备及高铁列车,这些应用场景为铝合金材料缺陷无损检测提供了良好的机遇。然而,高温环境下铝合金材料容易变软,粘性增大,易粘模,导致各种缺陷存在于材料中,对铝合金材料应用场景的安全运行构成严重威胁。因此,亟需研究新的缺陷无损检测方法,避免由于缺陷的存在而引发事故。
目前,针对铝合金材料缺陷的检测方法有:超声检测[3]、射线检测技术[4]、红外热成像[5]、电磁超声技术等[6]。这些无损检测方法都取得了良好的效果,但每一种检测方法仍存在一定的局限性,因此继续研究新的物理效应,探索新的检测方法仍是未来一段时间内的研究热点。
磁声电效应最早出现在生物医学成像领域,用于获取生物组织的电阻抗特性,在提高成像的分辨率及提高图像对比度方面取得了较好的效果[7-8]。20世纪90年代,Wen等[9]首先提出了磁声电成像,并建立了磁声电电阻抗成像理论基础。随后,Xu、Sun等[10-11]为了更好地重构电导率参数,对磁声电成像理论分析和实验设计进行的研究,促进了磁声电成像的进一步发展。Kunyansky[12]对低信噪比信号的反演重建算法进行了详尽研究,提出一整套磁声电成像电导率重建方法,并针对成像区域为立方体时构建了快速的电导率重建方法。Gong等[13]研究了线圈检测式磁声电成像的互易定理,建立了线圈感应式互易定理模型,推导了线圈感应电压信号与电导率之间的关系,并通过仿真和实验证明了该方法的正确性。Li等[14]对平面探头磁声电生物组织电导率成像进行了数值模拟和实验研究,获得了较好的轴线分辨率。本课题组前期开展了磁声电在生物组织中成像问题的研究[15-16],相关研究结果表明,在生物组织中磁声电成像最大的困难是重构异常组织中内部电导率分布,而对正常组织与异常组织之间的电导率边界成像效果较好,为此,本文考虑将生物组织中边界检测效果良好的磁声电成像方法用于非铁磁材料缺陷的无损检测。
本文首先建立声场正问题、电磁场正问题理论及基于互易定理条件下的理论模型;其次利用COMSOL仿真软件开展了仿真研究,从理论方面证明了该方法可行性,并求解了不同缺陷时对应的磁声电信号;最后搭建了实验平台,开展了相关实验,证明了该方法的有效性。
1 理论与方法与现有的检测方法相比,磁声电非铁磁材料缺陷无损检测具有如下优势。
1) 常规超声回波检测方法是通过接收反射的声波判断缺陷的有无及大小,由于声波的方向性强,当探头放置不当时会存在缺陷漏检现象。本研究仍用超声进行激励,保留了超声检测高的空间分辨率,但采用线圈接收感应电压信号能够有效克服因探头位置不当造成的漏检现象,同时也方便信号处理。
2) 涡流检测是利用电磁感应原理对导电材料缺陷进行检测的一种方法,然而受到涡流趋肤效应的影响,难以对深度的缺陷进行检测。本文所提出的磁声电缺陷检测法是利用超声波对待测构件进行激励,超声波能够有指向性地到达试件内部任何部位。同时,该方法不需要大的电流脉冲源,可降低检测成本、减小设备体积。
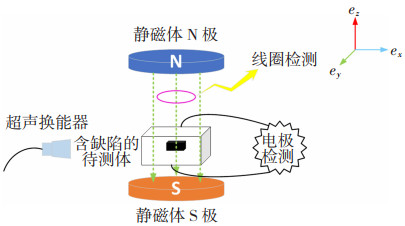
磁声电缺陷检测的主要原理如图 1所示。将待测构件置于磁感应强度为B0,方向为ez的静磁场中,在其周围的超声探头发射超声波(力源f0),方向为ex,超声在待测构件中传播引起带电粒子振动,假设其振动速度为v,在静磁场作用下产生动生电源Es=v×B0,进而在待测构件内产生随超声传播而变化的电流场分布J=σv×B0,利用电极或线圈可检测到相应的缺陷磁声电信号。将磁声电用于高电导率固体材料缺陷检测,与生物组织中电阻抗成像具有明显的区别,为此本文将对固体高电导率材料中磁声电缺陷检测进行理论建模。
|
图 1 磁声电缺陷检测原理图 Fig.1 Principle diagram of magneto-acousto-electrical defect detection |
根据所描述的磁声电缺陷检测原理,可知该方法属于声、电、磁多物理场耦合,涉及到声场正问题和电磁场正问题。本文首先针对声场正问题建立相应的数学物理模型,获得超声振动速度后,再建立电磁场数学物理模型。在高电导率材料中,磁声效应难以忽略,为此建立存在磁声效应条件下声场的数学模型。
假设被测构件满足各向同性条件,考虑洛伦兹力产生声波的情况下,铝合金材料中声波满足Navier方程[17]
| $ (\lambda+\mu) \nabla \nabla \cdot \boldsymbol{u}+\mu \nabla^2 \boldsymbol{u}+\boldsymbol{f}=\rho \frac{\partial^2 \boldsymbol{u}}{\partial t^2} $ | (1) |
式中:u为位移矢量;f=J×B为单位体积洛伦兹力;ρ为媒质质量密度;λ和μ分别为Lame第一和第二参数。由于多物理场通过声场的振动速度耦合,为此,对式(1)求导可得声波振动速度,
| $ (\lambda+\mu) \nabla \nabla \cdot \boldsymbol{v}+\mu \nabla^2 \boldsymbol{v}+\frac{\partial \boldsymbol{f}}{\partial t}=\rho \frac{\partial^2 \boldsymbol{v}}{\partial t^2} $ | (2) |
对式(2)进行赫姆霍兹分解,声波的振动速度可分解为任意标量的梯度与任意矢量的旋度,即v=▽φ+▽ ×ψ, ▽ ·ψ=0。本文采用纵波垂直入射的方式进行声激励,当纵波垂直入射到固体检测材料中,此时,不发生波型转换,在检测材料中仅出现纵波,声波振动速度可简化为
| $ \boldsymbol{v}=\nabla \varphi $ | (3) |
类似地,单位体积体力f可分解为式(4)
| $ \boldsymbol{f}=\nabla F $ | (4) |
将式(3),(4)代入到(2)得式(5)。
| $ \begin{aligned} & (\lambda+\mu) \nabla \nabla \cdot(\nabla \varphi)+\mu \nabla^2(\nabla \varphi)+(\nabla \dot{F})= \\ & \quad \rho(\nabla \ddot{\varphi}) \end{aligned} $ | (5) |
对式(5)进行化简后得式(6)
| $ \nabla\left[(\lambda+2 \mu) \nabla^2 \varphi+\dot{F}-\rho \ddot{\varphi}\right]=0 $ | (6) |
式(6)在整个空域和时域均成立,因此
| $ v_{\mathrm{p}}^2 \nabla^2 \varphi+\frac{1}{\rho} \frac{\partial F}{\partial t}=\frac{\partial^2 \varphi}{\partial t^2} $ | (7) |
式中:
| $ \frac{\partial \boldsymbol{v}_1}{\partial t} \cdot \boldsymbol{n}=\frac{\partial \boldsymbol{v}_2}{\partial t} \cdot \boldsymbol{n} $ | (8) |
式中:v1和v2分别为边界两边材料中的粒子振动速度:n为边界法向分量。利用边界条件,可以求解式(7)得到速度势φ,再根据式(3)可求得声波的振动速度。
1.2 电磁场正问题假定待测样品区域用Ω表示,相应边界为∂Ω,样品电导率为σ,待测样品放置在磁感应强度为B0的静止磁场中,超声在待测样品中的振动速度为v。振动的粒子在磁场的作用下受到大小为F=qv×B0的洛伦兹力,由此产生局部电流源Js =σv×B0。与生物组织中磁声电成像不同,在高电导率材料中,磁声电效应产生的磁场不能忽略,此时,总磁感应强度BT =B0 +B,满足B=▽ ×A,A为磁声电效应产生的矢量磁位。
在局部电流源作用下测试样品中总的电流密度,表示为JT =σv×BT +σE0,其中E0 =-▽u- ∂A/∂t。将BT,E0代入到JT中,得待测样品中总电流密度为
| $ \boldsymbol{J}_{\mathbf{T}}=\sigma \boldsymbol{v} \times \boldsymbol{B}_0+\sigma \boldsymbol{v} \times \boldsymbol{B}-\sigma(\nabla u+\partial \boldsymbol{A} / \partial t) $ | (9) |
式中u为测试样品中分布电势。
由电流连续性定理有▽ ·JT =-∂ρ/∂t,又因▽ ·D=ρ,则
| $ \nabla \cdot \boldsymbol{J}_{\mathbf{T}}=-\nabla \cdot \partial \boldsymbol{D} / \partial t $ | (10) |
忽略位移电流,将式(9)代入式(10)并整理后可得
| $ \nabla \cdot\left[\boldsymbol{\sigma} \boldsymbol{v} \times\left(\boldsymbol{B}_0+\nabla \times \boldsymbol{A}\right)\right]=\nabla \cdot\left(\boldsymbol{\sigma} u+\frac{\partial \boldsymbol{A}}{\partial t}\right) $ | (11) |
由于本文建立的仿真模型周围是水媒质,近似认为没有电流流过边界,总电流法向分量为零,故
| $ \left.\left(\sigma \boldsymbol{v} \times \boldsymbol{B}_0+\sigma \boldsymbol{v} \times \nabla \times \boldsymbol{A}-\nabla u-\partial \boldsymbol{A} / \partial t\right) \cdot \boldsymbol{n}\right|_{\partial \mathit{\varOmega}}=0 $ | (12) |
由全电流定律▽ ×B=μJT +∂D/∂t,在忽略位移电流的情况下可得
| $ \nabla \times \mu^{-1}(\nabla \times \boldsymbol{A})=\boldsymbol{J}_{\boldsymbol{T}} $ | (13) |
将式(9)代入式(13)可得
| $ \begin{aligned} &\begin{aligned} \nabla \times \mu^{-1}(\nabla \times \boldsymbol{A})= & \sigma \boldsymbol{v} \times \boldsymbol{B}_0+\sigma \boldsymbol{v} \times(\nabla \times \boldsymbol{A})- \\ & \sigma(\nabla u+\partial \boldsymbol{A} / \partial t) \end{aligned} \end{aligned} $ | (14) |
根据声场正问题求得声波振速,联立方程及边界条件可得方程组:
| $ \left\{\begin{array}{l} \nabla \cdot\left[\sigma \boldsymbol{v} \times\left(\boldsymbol{B}_0+\nabla \times \boldsymbol{A}\right)\right]= \\ \nabla \cdot\left(\sigma \nabla u+\frac{\partial \boldsymbol{A}}{\partial t}\right) \\ \nabla \times \mu^{-1}(\nabla \times \boldsymbol{A})=\sigma \boldsymbol{v} \times \boldsymbol{B}_0+\sigma \boldsymbol{v} \times \\ (\nabla \times \boldsymbol{A})-\sigma(\nabla u+\partial \boldsymbol{A} / \partial t) \\ \left(\sigma \boldsymbol{v} \times \boldsymbol{B}_0+\sigma \boldsymbol{v} \times \nabla \times \boldsymbol{A}-\nabla u-\right. \\ \partial \boldsymbol{A} / \partial t)\left.\cdot \boldsymbol{n}\right|_{\partial \mathit{\varOmega}}=0 \end{array}\right. $ | (15) |
通过式(15)可以求得相应的A及检测构件中电势u的时空分布。
1.3 缺陷信号检测方法目前,针对缺陷信号检测可采用电场检测(电极检测)和磁场检测(线圈检测)及互易定理3种方法。电场检测中,首先,通过式(15)求得检测构件中电势的时空分布,然后,假设电极a和b放置在检测构件表面的位置为ra和rb两点,则检测到磁声电缺陷信号为
| $ u_{\mathrm{ab}}=u\left(r_{\mathrm{a}}, t\right)-u\left(r_{\mathrm{b}}, t\right) $ | (16) |
式中:u(ra, t)表示电极在位置ra处t时刻的电势;u(rb, t)表示电极在位置rb处t时刻的电势。
磁场检测法中,根据法拉第电磁感应定律及高斯定理,线圈中的感应电压可表示为
| $ u_{\mathrm{ab}}(t)=-\int_{\text {coil }} \frac{\partial \boldsymbol{B}}{\partial t} \cdot \mathrm{d} \boldsymbol{s}=\int_l \boldsymbol{E}_0 \cdot \mathrm{d} \boldsymbol{l} $ | (17) |
式中ds表示线圈所围表面的微分面积,磁感应强度B中包含电导率信息,因此,接收电压信号中含有缺陷信息。
互易定理检测法基本原理如图 2所示。包含两个过程:1)磁声电缺陷检测过程(正向过程),以超声换能器为激励源,在静磁场的作用下产生洛伦兹力从而产生局部电场源,设其电场强度为E′ 1,在待检测构件中产生电场强度及电流密度分别为E1和J1;2)利用磁声电缺陷检测过程的测量电极向检测构件内注入单位电流(逆向过程),对应的电场强度为E′ 2,在检测构件内部产生的电流密度J2。由互易定理有
| $ \int\limits_{\mathit{\varOmega}} \boldsymbol{J}_1 \cdot \boldsymbol{E}_2^{\prime}-\boldsymbol{J}_2 \cdot \boldsymbol{E}_1^{\prime} \mathrm{d} \mathit{\varOmega}=0 $ | (18) |

|
图 2 互易定理原理图 Fig.2 Principle diagram of reciprocity theorem: (a) positive process; (b) inverse process |
将E′ 1 =v×B,E′ 2 =-▽ϕ′ 2代入式(18), 可得
| $ \int\limits_{\mathit{\varOmega}} \boldsymbol{J}_1 \cdot \nabla \boldsymbol{\phi}_2^{\prime}+\boldsymbol{J}_2 \cdot(\boldsymbol{v} \times \boldsymbol{B}) \mathrm{d} \mathit{\varOmega}=0 $ | (19) |
根据矢量恒等式
| $ \nabla \cdot(u \boldsymbol{A})=u \nabla \cdot \boldsymbol{A}+\boldsymbol{A} \cdot \nabla u $ |
式(19)中第一项可变为
| $ \int\limits_{\mathit{\varOmega}} \boldsymbol{J}_1 \cdot \nabla \phi_2^{\prime}=\int\limits_{\mathit{\varOmega}} \nabla \cdot\left(\phi_2^{\prime} \boldsymbol{J}_1\right)-\phi_2^{\prime} \nabla \cdot \boldsymbol{J}_1 \mathrm{~d} \mathit{\varOmega} $ | (20) |
高电导率铝合金材料中, 在MHz频段满足,σ≥jωε, 忽略介电常数产生的效应,由散度定理及边界条件J1·n=0,式(20)可简化为
| $ \int\limits_{\mathit{\varOmega}}-\phi_2^{\prime} \nabla \cdot \boldsymbol{J}_1+\boldsymbol{J}_2 \cdot(\boldsymbol{v} \times \boldsymbol{B}) \mathrm{d} \mathit{\varOmega}=0 $ | (21) |
采用点电极在待测构件表面a和b注入电流I,此时▽ · J1=I[δ(r-ra)-δ(r-rb)],假设电流I为单位电流,故
| $ \int\limits_{\mathit{\varOmega}} \boldsymbol{J}_2 \cdot(\boldsymbol{v} \times \boldsymbol{B}) \mathrm{d} \mathit{\varOmega}=\phi_{2 \mathrm{a}}^{\prime}-\phi_{2 \mathrm{~b}}^{\prime}=u $ | (22) |
式(22)建立了电极检测磁声电缺陷信号u与注入电流对应的电流场J2之间的关系,其中的B=BT。
2 有限元模型与仿真由构建的理论模型可知,通过解析法难以满足求解的需求,且不同的求解对象,模型也不同。为此,研究数值求解方法,利用有限元方法(Finite Element Method, FEM)中的COMSOL仿真软件对磁声电缺陷无损检测所满足的方程进行数值模拟。
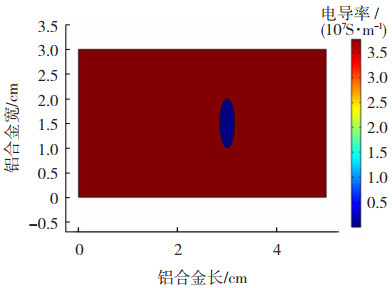
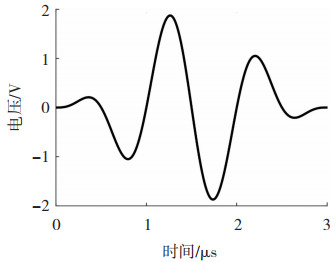
2.1 电极检测式铝合金磁声电缺陷检测仿真为了简化运算,在COMSOL Multiphysics软件中建立了内含缺陷的铝合金二维几何模型。其中铝合金试样尺寸为5 cm×3 cm,内部存在一个椭圆形缺陷,缺陷尺寸为:a半轴1.5 mm,b半轴5 mm,对应的电导率分布如图 3所示。采用如图 4所示波形作为超声激励源。
|
图 3 几何模型及对应电导率分布 Fig.3 Geometric model and corresponding conductivity distribution |
|
图 4 超声激励波形 Fig.4 Ultrasonic excitation waveform |
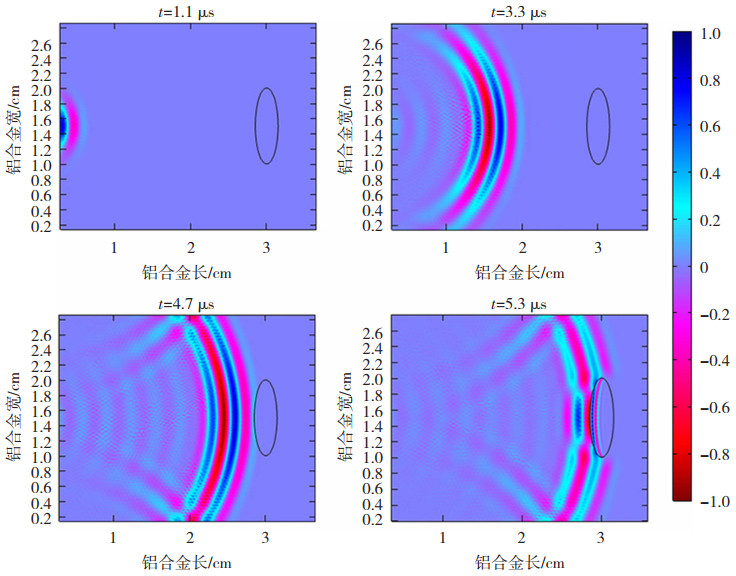
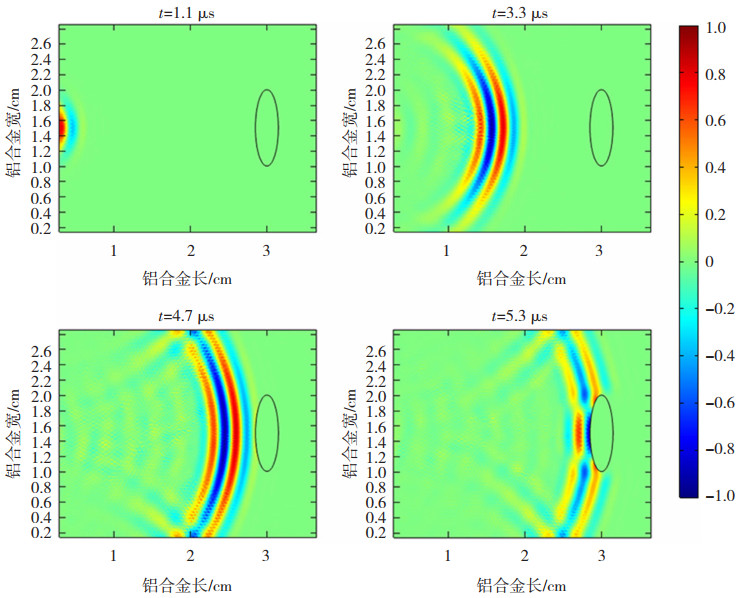
为了得到缺陷的磁声电信号,首先必须获得缺陷构件中粒子的振动速度,为此对声场正问题进行数值求解。图 5选取了缺陷构件中4个不同时刻t=1.1 μs,t=3.3 μs,t=4.7 μs,t=5.3 μs的粒子振动速度分布进行表征。t=1.1 μs为声波刚开始传播时构件中粒子振动速度分布;t=3.3 μs为声波传播一段时间后构件中粒子振动速度分布;t=4.7 μs为声波到达缺陷处时构件中粒子振动速度的分布情况;t=5.3 μs为声波进入缺陷后构件中粒子的振动速度分布。根据声波的传播速度与距离关系,可以验证所求振动速度的正确性。
|
图 5 不同时刻归一化粒子振动速度分布 Fig.5 Distribution of particle vibration velocity at different moments |
由声场正问题得到粒子振动速度后,对电磁场正问题进行数值求解,得出对应的电流密度分布情况如图 6所示。
|
图 6 不同时刻归一化外部电流密度分布 Fig.6 External current distribution at different moments |
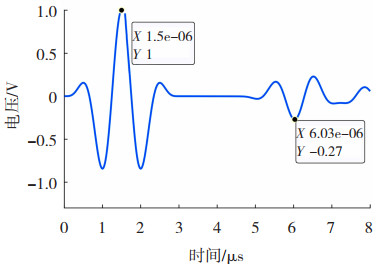
图 7为电极检测式所得到的归一化磁声电信号,可以看出,当声波传播到有电导率突变的界面处,才能够检测出明显的磁声电信号,且该信号与超声激励波形信号保持一致。第一信号为左边界信号,第二个信号为缺陷处磁声电缺陷信号,由于缺陷存在两个边界,因此信号产生一定程度的延伸。
|
图 7 电极检测式磁声电信号 Fig.7 Electrode-detected magneto-acousto-electrical signal |
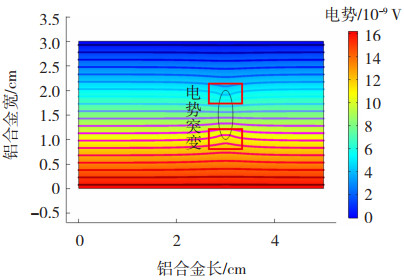
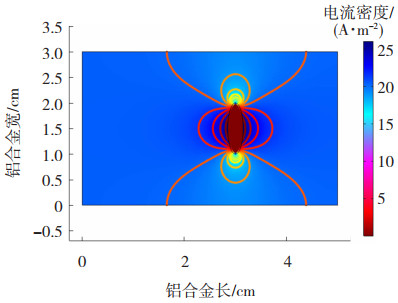
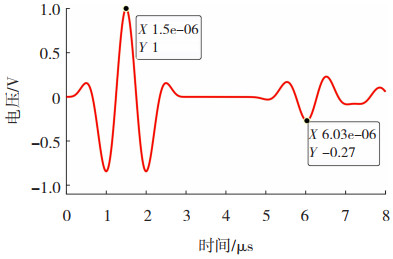
仍采用图 3所示的电极检测式仿真的几何模型,将缺陷构件上边界接地,使用电极在下边界中间位置施加1 V电压,可以得出如图 8所示的电势分布,从图 8可以看出在缺陷处存在电势突变。在此基础上,可以获得互易定理的Y方向电流密度分布,如图 9所示。根据公式(22)求出磁声电缺陷电压信号,如图 10所示,可以看出,通过互易定理能够检测出较好的磁声电电压信号。
|
图 8 互易定理的电势分布 Fig.8 Potential distribution of reciprocity theorem |
|
图 9 互易定理的Y方向电流密度分布 Fig.9 Distribution of current density in Y-direction for reciprocity theorem |
|
图 10 互易定理磁声电信号 Fig.10 Magneto-acousto-electrical signal for reciprocal theorem |
上述研究均是在缺陷内声波波长λ小于缺陷宽度L的情况下展开的。此时,超声波穿过缺陷左壁后,还未到达其右壁,即缺陷信号仅发生于左壁。当λ>L时,在透射作用下,超声波到达缺陷的右边界,此时,缺陷右壁对应的脉冲信号将与左壁对应的电信号发生混叠。本节将对缺陷宽度L与缺陷信号振幅绝对大小Y的关系进行分析。
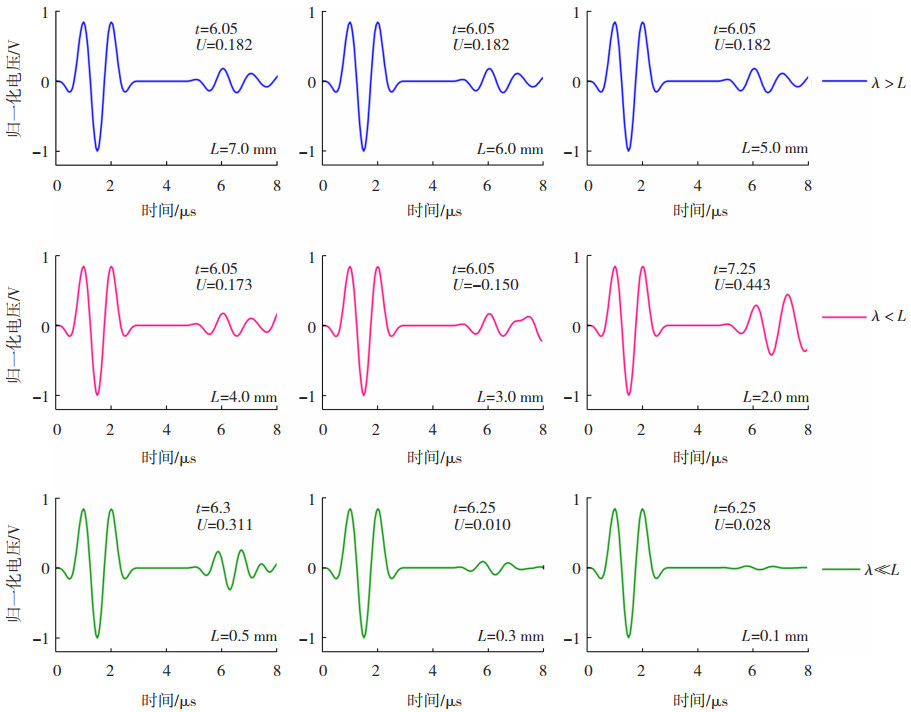
采用波长λ=4.5 mm信号对测试构件进行超声激励,缺陷处为空气媒质,改变缺陷宽度为7.0、6.0、5.0、4.0、3.0、2.0、0.5、0.3及0.1 mm,同时固定缺陷左壁与待测体左边界之间距离为2.9 cm,进行流-固-声-电磁场多物理场耦合求解,并绘制出电压信号随时间变化的一维曲线。由于在激励信号相同的条件下,待测体左边界产生的电信号相同,因此,以其振幅的绝对大小为1,对所得电压信号进行归一化处理,结果如图 11所示,结果表明:当缺陷宽度L大于波长λ时,缺陷电信号峰值时间t及幅值U均相同,其中t反应了缺陷的位置;当L小于λ时,缺陷左、右壁产生的电信号相互叠加,导致时间轴上也表现出一定的延拓,感应线圈采集到的缺陷脉冲振幅的绝对大小U与缺陷宽度L相关,这是因为边界信号叠加值与缺陷宽度有关所致。此时时间t也难以精确地定位缺陷;当L继续减小,即L≪λ时,缺陷左右壁对应的电信号近乎完全叠加且极性相反,因此,U将随着L的减小而单调递减。
|
图 11 缺陷宽度不同时对应的电信号 Fig.11 Electrical signals corresponding to different defect widths |
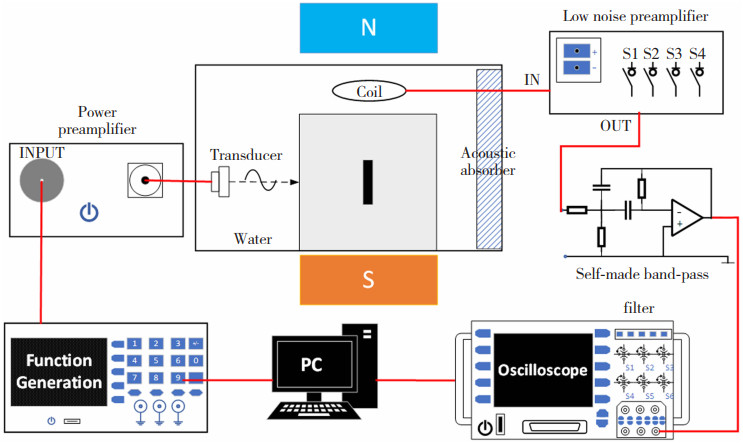
为了进一步验证本文所提出的磁声电缺陷检测方法的有效性,利用实际铝合金进行了以下实验,测试构件和实验原理分别如图 12,图 13所示。加工了一系列不同尺寸的缺陷测试材料,本文以尺寸为4 cm×4 cm×2 cm的长方体作为测试构件,其内部存在一个长方体缺陷,其尺寸为1 cm×0.5 mm×2 cm,此时,缺陷左壁距离铝合金左边界为2 cm。整个缺陷垂直穿过长方体构建的上下表面,水浸式超声换能器的频率为1 MHz,将其放置于铝合金构件的左侧,0.5TB的永磁体摆放于铝块底部。导线绕制的线圈陈列在铝块的正上方,作为该系统的数据采集装置。另外,该试验系统包括以下设备:数字示波器、功率放大器、前置放大器、函数发生器、自制滤波器(中心频率为1 MHz,带宽为300 kHz)以及计算机。

|
图 12 测试铝合金 Fig.12 Aluminum alloy tested |
|
图 13 实验原理图 Fig.13 Experimental schematic diagram |
考虑到空气与铝块的声阻抗差异过大,为了更为了更好地耦合超声波,将水浸式换能器、待测体一同置于装满水的水箱中。同时,为了防止声波在水箱边界发生反射,将声吸收橡胶贴附于水箱边界。任意函数发生器生成一束脉冲电压峰值达1 V、中心频率f=1 MHz、重复频率为100 Hz的脉冲,通过前置功率放大器放大后送入换能器中,换能器在脉冲的激励下产生超声波。一段时间后,利用低噪前置放大器及带通滤波器对线圈中采集到的电信号进行处理。
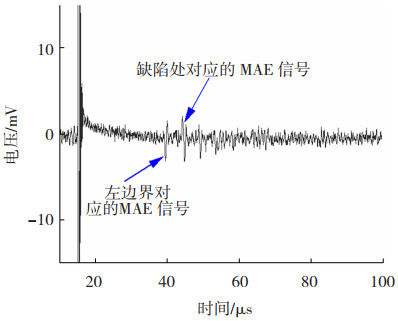
线圈所检测到的磁声电缺陷信号如图 14所示,结果表明,实验与仿真具有一致性,磁声电缺陷检测法能较好地呈现缺陷信号。
|
图 14 实验信号 Fig.14 Experimental signal |
本文提出了一种基于磁声电的铝合金材料缺陷检测新方法。
1) 基于固体力学与电磁场理论,建立了高电导率铝合金材料中的磁声电缺陷检测的固体声场及电磁场数学模型。后续仿真及实验验证了所建立的模型的正确性
2) 利用COMSOL Multiphysics软件分别对电极检测法及基于互易定理的检测法进行了数值模拟,并得到了粒子振动速度分布图、电流密度分布图、磁声电缺陷信号一维结果图等。模拟结果表明,电极检测法及基于互易定理的检测法方法得到的一维磁声电信号图具有一致性,证明了两种方法的正确性。
3) 通过搭建的实验平台,对不同缺陷尺寸的铝合金材料开展了实验研究。研究结果表明,缺陷位置误差约为0.05 cm,具有良好的检测精度。同时,实验与仿真结果具有一致性,证实了磁声电缺陷检测新方法的可行性。
| [1] |
陈新波, 何忠祥, 李小丽, 等. 基于数理统计的缺陷涡流检测定量方法[J]. 无损检测, 2020, 42(3): 50-54. CHEN Xinbo, HE Zhongxiang, LI Xiaoli, et al. Quantitative method of defect eddy current testing based on mathematical statistics[J]. NDT, 2020, 42(3): 50-54. |
| [2] |
涂彦昕, 刘立帅, 郭晨鋆, 等. 基于电磁感应热成像技术的复合绝缘子内部导通性缺陷检测方法[J]. 中国电机工程学报, 2021, 41(7): 2565-2576. TU Yanxin, LIU Lishuai, GUO Chenyun, et al. Detection method of internal conductivity defects of composite insulators based on electromagnetic induction thermal imaging technology[J]. Chinese Journal of Electrical Engineering, 2021, 41(7): 2565-2576. DOI:10.13334/j.0258-8013.pcsee.20178 |
| [3] |
ZHANG P, ZHANG X, CAO X, et al. Analysis on the tool wear behavior of 7050-T7451 aluminum alloy under ultrasonic elliptical vibration cutting[J]. Wear, 2021, 466: 203538. DOI:10.1016/j.wear.2020.203538 |
| [4] |
CHEN H, YANG Y, CAO S, et al. Fatigue life prediction of aluminum alloy 6061 based on defects analysis[J]. International Journal of Fatigue, 2021, 147: 106189. DOI:10.1016/j.ijfatigue.2021.106189 |
| [5] |
王博正, 董丽虹, 康嘉杰, 等. 激光红外热成像铝合金表面裂纹检测表面处理的研究[J]. 激光与红外, 2020, 50(11): 1358-1364. WANG Bozheng, DONG Lihong, KANG Jiajie, et al. Research on surface treatment of laser infrared thermal imaging aluminum alloy surface crack detection[J]. Laser and Infrared, 2020, 50(11): 1358-1364. |
| [6] |
THRING C B, FAN Y, EDWARDS R S. Multi-coil focused EMAT for characterisation of surface-breaking defects of arbitrary orientation[J]. NDT & E International, 2017, 88: 1-7. DOI:10.1016/j.ndteint.2017.02.005 |
| [7] |
LI Y, SONG J, XIA H, et al. Three-dimensional model of conductivity imaging for magneto-acousto-electrical tomography[J]. Journal of Applied Physics, 2020, 127(10): 104701. DOI:10.1063/1.5139600 |
| [8] |
DAI M, SUN T, CHEN X, et al. A b-scan imaging method of conductivity variation detection for magneto-acousto-electrical tomography[J]. IEEE Access, 2019, 7: 26881-26891. DOI:10.1109/ACCESS.2019.2899164 |
| [9] |
WEN H, SHAH J, BALABAN R S. Hall effect imaging[J]. IEEE Transactions on Biomedical Engineering, 1998, 45(1): 119-124. DOI:10.1109/10.650364 |
| [10] |
XU Y, HAIDER S, HRBEK A. Magneto-acousto-electrical tomography: A new imaging modality for electrical impedance[C]//13th International Conference on Electrical Bioimpedance and the 8th Conference on Electrical Impedance Tomography: ICEBI 2007, August 29th-September 2nd 2007, Graz, Austria. Springer Berlin Heidelberg, 2007: 292-295. DOI: 10.1007/978-3-540-73841-1_77
|
| [11] |
SUN T, HAO P, CHIN C T, et al. Rapid rotational magneto-acousto-electrical tomography with filtered back-projection algorithm based on plane waves[J]. Physics in Medicine & Biology, 2021, 66(9): 095002. |
| [12] |
KUNYANSKY L. A mathematical model and inversion procedure for magneto-acousto-electric tomography[J]. Inverse Problems, 2012, 28(3): 035002. DOI:10.1088/0266-5611/28/3/035002 |
| [13] |
GONG L, YANG L, YANG S, et al. Study on reciprocal models for magneto-acousto-electrical tomography with coil detection[J]. IEEE Access, 2019, 7: 154076-154083. DOI:10.1109/access.2019.2948731 |
| [14] |
LI Y, LIU G, XIA H, et al. Numerical simulations and experimental study of magneto-acousto-electrical tomography with plane transducer[J]. IEEE Transactions on Magnetics, 2017, 54(3): 1-4. DOI:10.1109/TMAG.2017.2771564 |
| [15] |
LV J, LIU G, WANG X, et al. A method of the forward problem for magneto-acousto-electrical tomography[J]. Technology and Health Care, 2016, 24(S2): 733-738. DOI:10.3233/thc-161202 |
| [16] |
刘国强. 磁声成像技术.下册, 电磁检测式磁声成像[M]. 北京: 科学出版社, 2016. LIU Guoqiang. Magneto-acoustic imaging technology. Volume Ⅱ, Magneto-acoustic imaging with electromagnetic detection[M]. Beijing: Science Press, 2016. |
| [17] |
沈建国. 应用声学基础——实轴积分法及二维谱技术[M]. 天津: 天津大学出版社, 2004: 101-125. SHEN Jianguo. Fundamentals of applied acoustics-real axis integration and two-dimensional spectral technique[M]. Tianjin: Tianjin University Press, 2004: 101-125. |
 2024, Vol. 32
2024, Vol. 32


