2. 中铁第一勘察设计院集团有限公司 建筑与规划设计研究院/TOD研发中心,西安 710043;
3. 西安建筑科技大学 土木工程学院,西安 710055
2. Research Institute of Architectural & Planning Design/Research Center of Transit Oriented Development, China Railway First Survey and Design Institute Group Co., LTD., Xi'an 710043, China;
3. School of Civil Engineering, Xi'an University of Architecture & Technology, Xi'an 710055, China
强烈地震作用所产生的大应变循环载荷,易使钢结构构件发生损伤和断裂。从材料层面而言,其属于高应力幅的低周疲劳(又称应变疲劳)。上世纪90年代中期发生在美国的北岭地震和日本的阪神地震是两次陆域型强震[1-2]。震后调查表明,多幢钢框架出现不同程度的损坏,大量梁柱节点因焊缝开裂致使结构倒塌[3-4]。因此,地震这种突发性、随机性和破坏性极强的地面运动,对高层钢结构建筑及大跨度钢桥梁将产生不可估量的损害。低周疲劳作用下钢材塑性损伤的不断累积,致使裂纹的萌生及扩展,且伴随着构件性能的显著退化,最终可能导致无明显预兆的脆性断裂破坏发生。因此,从结构健康监测的角度出发,对受疲劳载荷作用的钢结构进行损伤的识别与评估,才能保证服役期建筑物的安全运营。
基于无损检测技术识别服役期钢结构的损伤情况是健康监测系统中的重要一环。要实现对既有结构健康状况的检测与评估,必须完成由定性向定量的发展需求。为满足这一需求,国内外兴起了一系列基于不同物理、力学原理的无损检测技术,并在实际应用过程中不断提升和完善。其中,金属磁记忆检测技术,自20世纪90年末由俄罗斯学者Doubov[5-6]提出后,因其独特的优越性,曾受到国内外专家的广泛关注。该方法利用铁磁材料在地磁场和机械载荷作用下的自发漏磁信号来评估其早期损伤和缺陷发展情况[7-8]。其基本原理是,在地磁场及外荷载作用下,材料内部磁畴组织的定向及不可逆重新取向将导致应力集中及缺陷区域漏磁场发生改变,并在外部机械载荷撤去后仍然保留。磁场的不可逆变化“记忆”了构件表面的缺陷及应力集中位置,即称为磁记忆效应[9]。相比传统无损检测技术,金属磁记忆技术在检测过程中无需涂抹耦合剂、彻底清洗试件表面以及施加强的外磁场。更重要的是,其可在综合分析最大应力集中位置和损伤源的基础上,实现对可能损伤位置的预测,进而对铁磁元件进行早期诊断。
金属磁记忆检测技术对材料应力(应变)变化及其内部的微观裂纹萌生都具有一定的表征能力。国内外学者针对各类带预制缺陷的铁磁性钢构件,通过理论分析及试验验证的方法,研究了不同疲劳形式下(如拉-拉、拉-压、扭转、弯曲等)磁信号随疲劳损伤累积的变化情况。冷建成等[10]检测了扭转疲劳载荷下结构钢表面的漏磁场,结果表明法向磁场变化可间接反映材料的不同损伤状态。Huang等[11]分析了弯曲疲劳载荷下带缺陷试件表面的磁记忆信号,研究表明法向磁信号梯度最大值具有表征构件疲劳裂纹扩展的潜在可能。Liu等[12]研究指出,利用磁信号分量可较好地评判材料的早期疲劳损伤。Zhang等[13]对高周疲劳下钢筋的力-磁变化关系进行了试验及理论研究,并从机理上对结果进行了解释。
上述研究为金属磁记忆检测技术在铁磁性钢构件疲劳损伤表征方面的应用提供了参考。但现有研究仍缺乏针对低周疲劳问题的分析,而基于力-磁耦合机理,建立累积塑性损伤与磁信号变化关系的研究更是鲜有报道。究其原因:首先是有关低周疲劳下结构钢的力-磁耦合理论研究尚不成熟;其次,焊接试件的几何截面变化使得其内部应力场分布不均,造成了非均匀磁化的问题。
为此,本文针对焊接件非均匀磁化问题,结合既有理论,改进模拟方法,实现了低周疲劳下V型坡口焊接试件的力-磁耦合有限元模拟方法。同时,通过低周疲劳实验和磁信号检测实验,采集并分析了Q345qC焊接试件表面的法向磁记忆信号HSF(z)及其特征参数的变化规律,并将有限元分析结果与实验结果进行比较,提出损伤与磁信号特征值之间的量化关系。
1 有元模拟 1.1 本构模型模拟过程涉及3个分析模块,即力学模块、疲劳模块及力-磁耦合本构关系,三者构成了磁-机械耦合的理论框架。结构力学模块采用线弹性模型及混合强化模型,目的在于得到疲劳稳定循环下各节点上的塑性应变。混合强化模型考虑了随动强化部分及各向同性强化部分的共同作用,可以更好地描述钢材加载过程中所产生的包辛格效应和快速应力应变强化现象。疲劳模块采用Coffin-Manson应变寿命疲劳模型,旨在计算材料在低周疲劳状态下的疲劳寿命。在力-磁耦合本构关系中,采用基于应变的J-A(Jiles-Atherton)磁滞回模型作为桥梁来描述累积塑性应变引起的磁化强度的改变。最后,在磁场模块中通过不同的磁化本构,计算了试件表面的磁场强度。
1.1.1 线弹性模型及混合强化模型对于一般钢材,弹性变形时可采用线弹性本构模型,如式(1)所示。
| $ \varepsilon_{i j}=\frac{1+v}{E} \sigma_{i j}-\frac{v}{E} \sigma_{k k} \delta_{i j} $ | (1) |
式中:εij为应变张量;σij为应力张量;σkk为x、y、z 3个方向主应力之和;δij为增量函数;E为弹性模量;υ为泊松比。
塑性阶段,使用与塑性势关联的Von Mises屈服面准则,并定义初始屈服强度以描述塑性变形开始时的应力水平。对于钢材的低周疲劳问题,采用混合强化模型作为循环本构模型进行分析[14],其包括等向强化模型和随动强化模型两个部分,如式(2)和(3)所示。
| $ \sigma_{\mathrm{ys}}=\sigma_{\mathrm{y} \mathbf{s} 0}+\sigma_{\mathrm{sat}}\left(1-\mathrm{e}^{-\beta \varepsilon_{\mathrm{pe}}}\right) $ | (2) |
式中:σys为屈服面;σys0为等效塑性应变为零时的应力,本文取初始屈服强度;σsat为饱和流动应力,其反应了屈服面尺寸的最大变化值;β为饱和指数,其反映了屈服面随塑性应变发展的变化规律;εpe为有效塑性应变。
| $ \left\{\begin{array}{l} \dot{\sigma}_{\mathrm{b}, i}=\frac{2}{3} C_i \dot{\varepsilon}_{\mathrm{p}}-\gamma_i \dot{\varepsilon}_{\mathrm{pe}} \sigma_{\mathrm{b}, i} \\ \sigma_{\mathrm{b}}=\frac{2}{3} C_0 \varepsilon_{\mathrm{p}}+\sum\limits_{i=1}^{N_{\mathrm{f}}} \sigma_{\mathrm{b}, i} \end{array}\right. $ | (3) |
式中:
低周疲劳载荷下,构件大部分已进入塑性阶段,但由于焊接试件截面的不均匀变化,局部的非弹性变形会造成明显的应力集中现象。针对此类疲劳问题,常在疲劳分析模块中使用应变寿命的疲劳模型(Coffin-Manson模型)(式(4))来计算并获取材料在低周疲劳模式下的疲劳寿命[15]。
| $ \left\{\begin{array}{l} \varepsilon_{\mathrm{a}}=\varepsilon_{\mathrm{f}}^{\prime} \cdot\left(2 N_{\mathrm{f}}\right)^c \\ \varepsilon_{\mathrm{a}}=\Delta \varepsilon_i / 2 \end{array}\right. $ | (4) |
式中:εa为塑性应变幅;ε′f为疲劳延性系数;c为疲劳延性指数;Nf为疲劳寿命;Δεi为一次循环加载下的累积塑性应变。
1.1.3 基于应变的磁滞回本构模型本文采用马小平、苏三庆等[16-17]提出的基于应变的磁滞回本构模型,作为低周疲劳下对接焊缝的力-磁耦合模型。基于J-A磁-机械理论与磁滞回理论所构建的基于应变的磁滞回本构模型,可合理表征塑性循环载荷下磁化强度与累积塑性应变的量化关系。其中,磁化强度的计算表达式为
| $ M=M_{\mathrm{an}}-\frac{\left(G_1+G_2 / d\right)\left[A_{\mathrm{e}} \varepsilon_{\mathrm{tr}}^{1 / 2} /\left(\alpha_{\mathrm{k}} G b\right)+\rho_0^{1 / 2}\right]}{\mu_0 /\left(k_0 \delta \mathrm{~d} M / \mathrm{d} H_{\mathrm{eff}}\right)} $ | (5) |
式中:M为磁化强度;Man为非滞后磁化强度;k0为未成形状态下的初始钉扎系数,其描述了初始状态下材料内部固有缺陷对于磁畴运动的阻碍程度;参数δ的目的是确保钉扎总是阻碍磁化强度的变化。当场强H在正方向,dH/dt>0增加时,δ取+1;当场强H在负方向,dH/dt < 0增加时,δ取-1。μ0为真空磁导率;G1、G2和d为常数;Ae是与应力有相同量纲的参数;αk为常数,其大小为0.76;G为剪切模量;b为伯格斯矢量的值;ρ0为未成形状态的初始位错密度;Heff为有效场;εtr为累积残余塑性应变。
非滞后磁化强度Man的表达式为
| $ \begin{aligned} M_{\mathrm{an}} / M_{\mathrm{s}}=\operatorname{coth}\left[\frac{H_{\mathrm{eff}} /\left(a_0 G_1+a_0 G_2 / d\right)}{A_{\mathrm{e}} \varepsilon_{\mathrm{tr}}^{1 / 2} /\left(a_{\mathrm{k}} G b+\rho_0^{1 / 2}\right)}\right]- \frac{A_{\mathrm{e}} \varepsilon_{\mathrm{tr}}^{1 / 2} /\left(a_{\mathrm{k}} G b+\rho_0^{1 / 2}\right)}{H_{\mathrm{eff}} /\left(a_0 G_1+a_0 G_2 / d\right)} \end{aligned} $ | (6) |
式中:Ms为饱和磁化强度;a0为未成形状态下的初始比例系数。
有效场Heff的表达式为
| $ \begin{aligned} H_{\text {eff }} & =H+\alpha M- \frac{\left(\gamma_1-\gamma_1^{\prime} A_{\mathrm{e}} \varepsilon_{\mathrm{tr}}^{1 / 2}\right) M+2\left(\gamma_2-\gamma_2^{\prime} A_{\mathrm{e}} \varepsilon_{\mathrm{tr}}^{1 / 2}\right) M^3}{\mu_0 /\left(3 \nu^{\prime} A_{\mathrm{e}} \varepsilon_{\mathrm{tr}}^{1 / 2}\right)} \end{aligned} $ | (7) |
其中:H为环境磁场;α为耦合系数;γ1、γ′1、γ2、γ′2为磁致伸缩应变关于磁化强度的拟合系数;ν′为应变相关系数。
累积残余塑性应变εtr的表达式为
| $ \varepsilon_{\mathrm{tr}}=\sum\limits_{i=0}^{N_{\mathrm{f}}} \varepsilon_i^{\mathrm{r}}=\sum\limits_{i=0}^{N_{\mathrm{f}}}\left(\varepsilon_i^{\mathrm{p}}-\frac{\sigma_i^{\mathrm{F}}}{E}\right) $ | (8) |
其中,
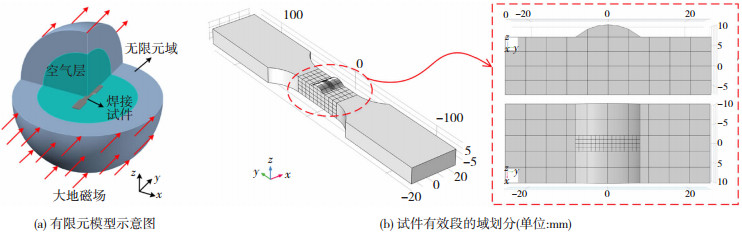
焊接试件的力-磁耦合有限元模型由试件、空气层及无限元域3部分组成。图 1(a)为模型示意图。焊接试件因截面形状不均匀变化会有应力集中产生,地磁场环境下应力集中区塑性应变的不均匀分布将导致试件内部非均匀磁化的产生。为此,本文提出了用多个域的应力代表值来计算相应的磁化强度,以更准确地描述循环载荷作用下焊接区磁化的非均匀变化。将试件有效拉-压段的域进行划分,划分后的模型如图 1(b)所示。为确保数据采集的准确性,对焊接区数据采集点处的域进行加密。
|
图 1 焊接试件有限元模型的构建 Fig.1 Construction of finite element model for welded specimen: (a) schematic diagram of FEA model; (b) domain division of effective segment |
通过布尔运算及模型组装后,对其进行网格划分,如图 2(a)和(b)所示。考虑到计算结果的准确性及求解效率,对各部分区域均采用自由四面体单元。如图 2(c)所示,力场模块中,在试样两端的夹持段分别施加固定约束和三角波的周期性位移载荷。磁场模块中,对试件有效段内的各个域,采用磁化本构(式(9)),将计算的磁化强度进行赋值和计算。对试件加持段及过渡段、外包空气层及无限元域采用磁导率本构方程(式(10)),以满足静磁场分析的需要。
| $ \boldsymbol{B}=\mu_0\left(\boldsymbol{H}+\boldsymbol{M}+\boldsymbol{M}_0\right) $ | (9) |
| $ \boldsymbol{B}=\mu_0 \mu_{\mathrm{r}} \boldsymbol{H} $ | (10) |
式中:μr为材料相对磁导率;H为环境磁场的矢量;M为外荷载引起的磁化;M0为试样初始磁化强度。

|
图 2 焊接试件有限元模型的网格和边界条件(单位:mm) Fig.2 Mesh and boundary conditions for finite element model for welded specimens: (a) meshed model; (b) mesh refinement of effective segment; (c) boundary conditions and magnetization constitutive |
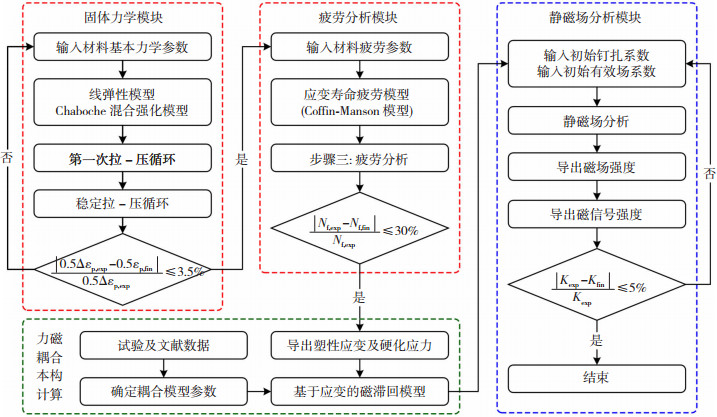
有限元模拟过程如图 3所示。首先,在固体力学模块中,计算得到稳定循环下所有域的半周期有效塑性应变及半周期应变硬化应力。然后,根据静力分析结果,进一步在疲劳模块中计算得到材料的疲劳寿命。
|
图 3 低周疲劳作用下焊接试件的力-磁耦合模拟流程 Fig.3 Mechanical-magneto coupling simulation flow of butt welding specimen under low cycle fatigue |
通过力学模块及疲劳模块计算得到累积塑性应变,并将其带入磁-机械本构模型中,求得对应域的磁化强度。最后,通过静磁场分析,得到焊接试件在不同疲劳载荷下的磁场变化。其中,0.5Δεp, exp为实验得到的稳定循环下的名义塑性应变幅值;0.5Δεp, fin为有限元计算获得的稳定循环下的名义塑性应变幅值;Nf, exp为实验获得的疲劳寿命;Nf, fin为有限元计算获得的疲劳寿命;Kexp为实验分析得到的磁信号曲线峰-谷梯度值;Kfin为通过有限元计算获得的磁信号曲线峰-谷梯度值。图 3中所示的相对误差(3.5%、30%、5%)是先根据分析变量拟定初始值,而后以实验值与模拟值相互契合为目标,通过迭代试算而确定的。
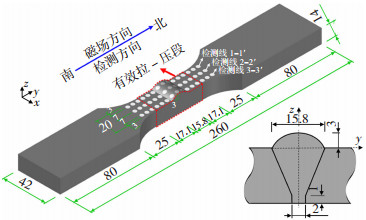
2 实 验 2.1 试件制备选取14 mm厚Q345qC钢板制备试件,其化学成分列于表 1。按照国标(GB/T 8110—2008)[18],采用CO2气体保护焊制备单面V形坡口焊接试件。根据国标(GB/T 15248—2008)[19],设计加工11个Q345qC试件用于低周疲劳实验及磁信号检测,试件几何尺寸如图 4所示。S-1至S-2试件用以确定焊接试件的基本力学性能(见表 2),其中,E为弹性模量,εy为屈服应变,σy为屈服强度,εu为极限应变,σu为极限强度,A为伸长率。试件S-3至S-5用于确定试件的低周疲劳寿命、采集磁信号所需的合理加载圈数;S-6至S-11用于采集不同循环载荷下的磁信号。
| 表 1 Q345qC钢的化学组成(质量分数/%) Table 1 Chemical composition of Q345qC steel (wt.%) |
|
图 4 V形坡口焊接试件的尺寸及检测点布置(单位:mm) Fig.4 Geometric dimension and measuring points of butt welding specimens with V-groove |
| 表 2 Q345qC焊接试件的力学性能参数 Table 2 Mechanical properties parameters of Q345qC welded specimens |
所有试件在加载前均使用国产CFW-2000退磁机进行退磁处理,以消除试件在制备过程中所产生的残余磁化。按不同应变幅值对Q345qC焊接试件进行低周疲劳实验。在试样的测量截面上安装一个轴向45 mm夹式引伸计,以控制总应变并获取应力应变数据。以载荷下降15%、且出现明显裂纹时判定试件失效。首先,按照应变幅0.4%、0.6%、0.8%,分别对S-4、S-5、S-6试件进行低周疲劳实验,直至断裂失效,获得不同应变幅下构件的疲劳寿命,并确定采集磁信号所需的合理停机圈数。根据不同实验的疲劳寿命,确定试件S-7、S-8、S-9、S-10、S-11试件的加载圈数分别为70、140、280、350、564 cycle,各试件加载应变幅为0.6%。将每个试件加载至所需的循环圈数后,停机将试件从夹具上取下,沿地磁场方向(即南北方向)将其放置在非铁磁性平台上进行测量,提离值高度为1 mm。采集试件表面3条检测线上的磁信号法向分量HSF(z),检测点布置如图 4所示。每个测点测量3次,计算平均值。
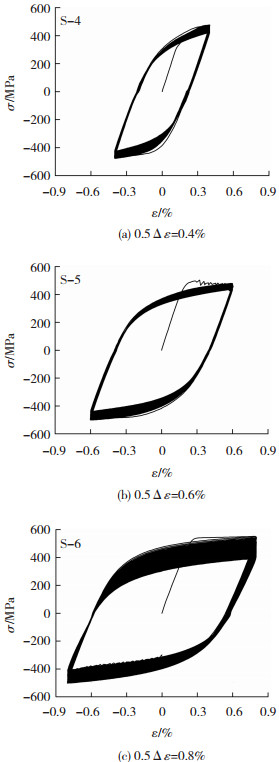
2.3 实验结果 2.3.1 低周疲劳实验结果低周疲劳下焊接试件的名义应力-应变滞回曲线如图 5所示,可以看出,曲线基本呈梭形。在第1次循环中,滞回曲线与单轴拉伸状态类似。随着循环载荷的增加,试件进入稳定循环阶段,此时曲线的形状基本保持不变。在加载后期,滞回曲线的峰值应力逐渐下降,材料刚度明显退化,在荷载下降15%时,其表面出现明显裂缝,试件失效。
|
图 5 不同应变幅下的名义应力(σ)-应变(ε)曲线 Fig.5 Nominal stress-strain curves under different strain amplitudes |
低周疲劳实验结果如表 3所示。其中,0.5Δε、0.5Δεe、0.5Δεp、0.5Δσ、0.5ΔσF和Nf分别为总应变幅、弹性应变幅、塑性应变幅、应力幅、应变硬化应力幅和失效循环次数。根据表 3的实验结果及文献[20],结合弹、塑性应变幅与疲劳寿命之间的关系(式(11)),可拟合得到Q345qC焊接试件的应变-寿命曲线,如图 6所示。其中,σ′f、ε′f、b及c分别为疲劳强度系数、疲劳延性系数、疲劳强度指数和疲劳延续指数,见表 4。
| $ \left\{\begin{array}{l} 0.5 \Delta \varepsilon_{\mathrm{e}}=\frac{\sigma_{\mathrm{f}}^{\prime}}{E}\left(2 N_{\mathrm{f}}\right)^b \\ 0.5 \Delta \varepsilon_{\mathrm{p}}=\varepsilon_{\mathrm{f}}^{\prime}\left(2 N_{\mathrm{f}}\right)^c \end{array}\right. $ | (11) |
| 表 3 Q345qC焊接试件的低周疲劳实验结果 Table 3 Low cycle fatigue test results of Q345qC weldments |

|
图 6 Q345qC焊接试件的应变-寿命曲线 Fig.6 Strain-life curve of Q345qC welding specimen: (a) elastic strain amplitude; (b) plastic strain amplitude |
| 表 4 Q345qC焊接试件应变-寿命拟合曲线参数 Table 4 Parameters of strain-life fitting curve for Q345qC welding specimen |
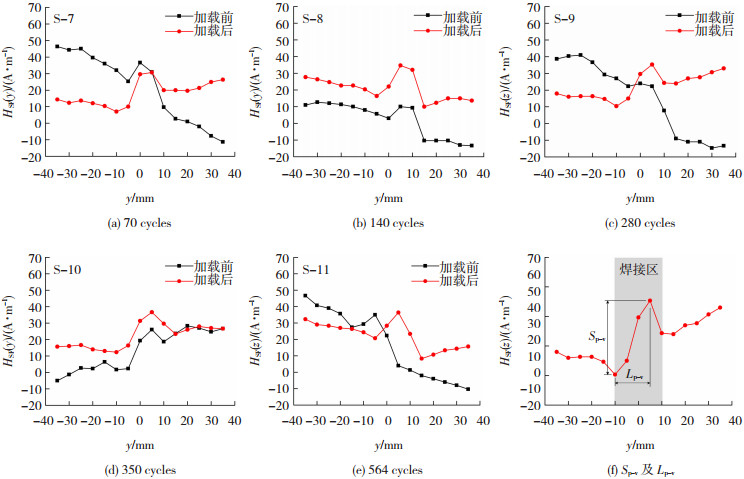
提取应变幅为0.6%时不同循环载荷下焊接试件表面检测线2-2′上的磁信号曲线,结果如图 7(a)~(e)所示,可以看出,磁信号曲线在焊接区域出现了明显的突变现象,且相比初始未加载阶段,加载后磁信号曲线的突变程度有所减小。同时,加载后磁信号曲线相对于初始状态整体发生转动,磁信号曲线的整体斜率显著变化。不同循环载荷下磁信号曲线均在左侧出现波谷、右侧出现波峰。
|
图 7 不同循环载荷下的磁信号曲线及特征变化 Fig.7 HSF(z)in different cyclic loads and characteristic variation |
在焊接区域几何形状不变的情况下,磁信号突变主要受外载荷与地磁场耦合作用的影响。该影响一方面包括焊缝余高处累积塑性应变的不断增加,另一方面包括整体磁化强度改变而引起的磁信号曲线整体斜率的变化。鉴于此,本文提取磁信号曲线上波峰-波谷差值Sp-v和波峰-波谷距离Lp-v,如图 7(f)所示,并以波峰-波谷梯度Kp-v=Sp-v/Lp-v作为磁特征判别量进行分析。不同循环载荷的磁特征判别量见表 5,其中,N为循环载荷次数。磁信号曲线上的峰-谷梯度值Kp-v随着循环载荷的增加呈现出一定的变化规律。
| 表 5 不同循环载荷下焊接区磁信号特征值 Table 5 Magnetic characteristic parameters in welding region under different cyclic loads |
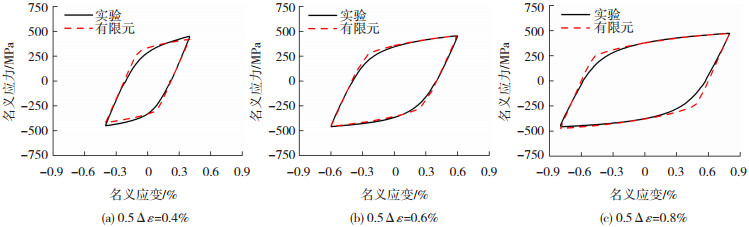
根据低周疲劳实验结果及文献[21]的数据,确定混合强化模型材料参数,计算得到稳定循环下的名义应力-应变曲线,并与实验结果进行比较,如图 8所示,可以看出,在稳定循环下,有限元得到的名义应力-应变滞回曲线与实验结果基本一致,表明本文所采用的混合强化模型是准确的。
|
图 8 稳定循环下应力-应变滞回曲线对比 Fig.8 Comparison of stress-strain hysteresis curves under stable cycle |
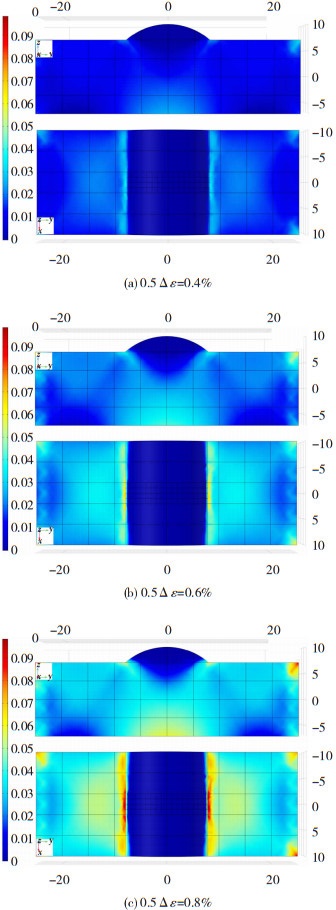
图 9为稳定循环下不同试件达到应变幅值时的累积塑性应变云图。
|
图 9 稳定循环下各焊接试件的塑性应变云图(单位:mm) Fig.9 Nephogram of plastic strain for weldment under stable cycle |
由图 9可见,随着应变幅的增加,试件表面焊趾位置处由于应力集中的存在会使有效塑性应变明显增大。疲劳过程中材料内部塑性应变的不断累积,不仅直接影响疲劳寿命,而且会导致磁化强度的改变。在有限元分析中应密切关注稳态循环下塑性应变幅值的准确性。因此,本文进一步提取了有限元计算的名义塑性应变幅与实验结果进行比较,结果见表 6,可以看到有限元计算结果与实验结果的平均误差为2.20%,模拟结果较为精确。
| 表 6 塑性应变幅的对比 Table 6 Comparison of plastic strain amplitudes |
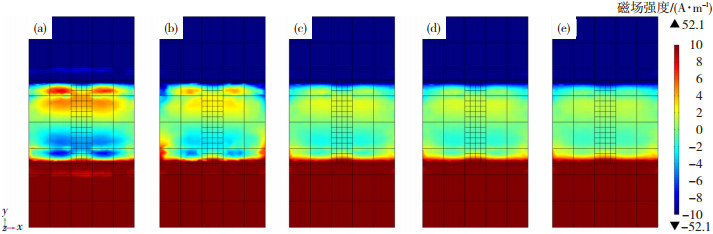
根据文献[22-24]确定磁滞回模型中的相关参数,G1=0.5×10-6 m,G2=10×10-12 m2,d=20×10-6 m,αk=0.76,b=2.5×10-10 m,ρ0=1×1012 m-2,Ae=1.369 9×109 Pa。根据文献[25]确定磁-机械本构模型中的相关参数,α=0.001,Ms=1.7×106 A/m,H=40 A/m,μ0=4π×10-7 H/m,γ1=7×10-18 A-2 ·m2,γ′1=7×10-18 A-2 ·m2,γ2=-3.3×10-30 A-4 ·m4,γ′2=2.1×10-38 A-4 ·m4 ·Pa-1,a0=688 0 A/m,k0=3.197 2π×10-7 A/m。弹性模量E及剪切模量G通过拉伸实验数据确定。基于此,按照所述模拟流程即可计算得到循环载荷下焊接试件的磁场变化,如图 10所示。由图 10可以看出,法向磁场强度在焊趾位置及弹塑性域交界处出现了较为明显的突变,并且随循环载荷增加,磁场强度逐渐减小。
|
图 10 不同循环载荷下焊接试件表面的法向磁场强度云图 Fig.10 Nephogram of normal magnetic field intensity for weldment: (a) 70 cycles; (b) 140 cycles; (c) 280 cycles; (d) 350 cycles; (e) 564 cycles |
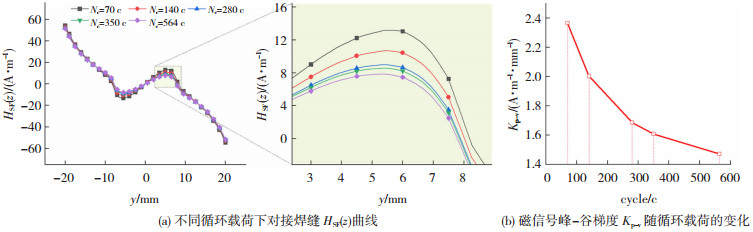
不同循环载荷下试件表面的HSF(z)信号曲线如图 11(a)所示,可以看出,试件表面的磁信号曲线沿检测线方向发生了由正向负的转变,且在焊缝区域出现了明显的波峰、波谷突变。磁信号曲线上波峰、波谷的幅值随着循环圈数的增加有逐渐减小的趋势。进一步提取磁信号峰-谷梯度值作为磁特征判别量,并与循环载荷建立联系,如图 11(b)所示,可以看出,随着循环圈数的增加,磁信号曲线上的峰谷梯度值Kp-v呈非线性减小。
|
图 11 低周疲劳下焊接试件的力-磁耦合有限元模拟结果 Fig.11 Magneto-mechanical coupling simulation results for weldment under LCF: (a) HSF(z) curves under cyclic loads; (b) variation of peak-valley gradient Kp-v with cyclic load |
恒定塑性应变幅的低周疲劳中,材料的疲劳累积损伤D可表示为[26]
| $ D=\frac{1}{C^{1 / m}} \sum\limits_{i=1}^{N_{\mathrm{f}}}\left(\varepsilon_i^{\mathrm{p}}\right)^{1 / m} $ | (12) |
式中,C和m是基于Coffin-Manson定律并通过拟合低周疲劳实验数据(图 6(b))获得的。
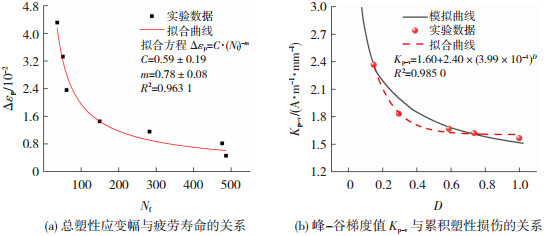
根据低周疲劳的实验结果,可得Q345qC焊接试件总塑性应变幅Δεp随疲劳寿命Nf的变化曲线,如图 12(a)所示。由于焊接试件的疲劳寿命在焊接质量的影响下存在较大的离散性,因此,为了更好地与本实验得到的数据进行对比分析,确定C=0.776 1,m=0.737 9。基于此,可得磁信号峰-谷梯度随累积塑性损伤的变化曲线,并与实验结果进行对比,如图 12(b)所示。结果表明,有限元模拟得到的Kp-v-D关系与实验数据基本一致,随着损伤的增加,Kp-v均呈非线性的减小。对比结果证明了本文提出的有限元模拟方法的可行性。
|
图 12 低周疲劳下焊接试件损伤与磁信号特征参量的关系 Fig.12 Relationship between weldment damage and magnetic signal characteristic parameters under LCF: (a) relationship between total plastic strain amplitude and fatigue life; (b) relationship between peak-valley gradient Kp-v and cumulative plastic damage |
本文进一步对比不同损伤程度下模拟和实验得到的峰-谷梯度值,结果如表 7所示,可以看出,实验和模拟之间的相对误差最大为9.243 1%。这可能是实验中实际焊接节点与有限元模型之间焊接形貌差异所致。同时,在检测过程中实验环境对磁信号存在一定干扰,因而导致实验所得的磁信号特征值有所浮动。整体上看,二者相对误差的平均值为3.542 4%,在可接受的范围内。因此,可采用这种模拟方法对低周疲劳载荷下对接焊缝的累积塑性损伤进行仿真分析。
| 表 7 不同损伤程度下实验与模拟中磁信号峰-谷梯度值Kp-v的对比 Table 7 Comparison of peak-valley gradient in experiment and simulation under different damage levels |
综上分析,峰- 谷梯度值Kp-v和损伤D之间的关系可通过非线性拟合得到,如式(13)所示。
| $ K_{\mathrm{p}-\mathrm{v}}=A-B \cdot C^D $ | (13) |
其中,参数A、B、C分别是与荷载的类型和大小、材料类型、试件的几何形状及尺寸、初始磁化强度、提离值等有关的参数。
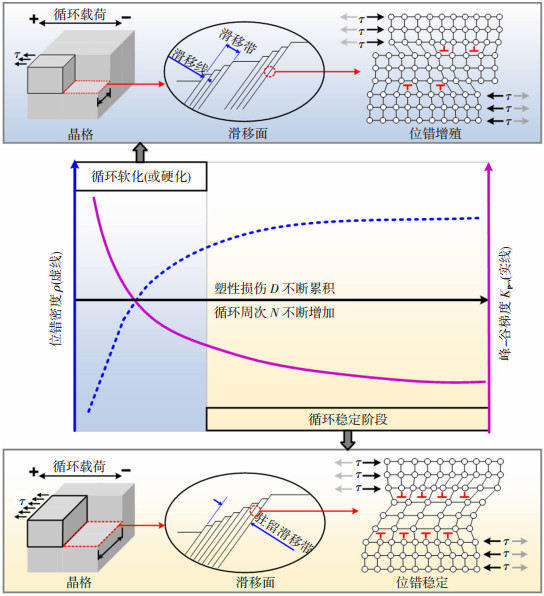
模拟结果与实验数据的对比表明,磁信号峰-谷梯度值Kp-v和累积延性损伤D表现出一致的指数递减趋势,该变化可从位错活性和增殖的微观机理角度来解释,如图 13所示。
|
图 13 位错密度和峰-谷梯度随累积塑性损伤的变化机理 Fig.13 Mechanism of dislocation density and peak-valley gradient with cumulative plastic damage |
常应变幅的低周疲劳载荷作用下,铁磁体内部晶粒急剧产生大量的位错滑移线,形成滑移带,位错密度较初始状态显著增加。随着循环圈数的不断累加,位错滑移带逐渐变宽,滑移带上的滑移线密度不断增大,但循环载荷下滑移带始终停留在原始位置,表现为空间层状位错结构,形成驻留滑移带,位错密度趋于稳定。根据疲劳累积损伤关系可知,累积延性损伤D随着循环次数N的增加呈单调递增。综上所述,随着循环圈数的增加,延性损伤不断累积,材料内部的位错密度呈非线性递增,磁化强度M呈非线性递减,二者变化率均先急剧变化,而后趋于平缓。磁信号峰-谷梯度Kp-v与磁化强度M呈正相关,故也呈现出指数递减的变化趋势[27-28]。因此,通过理论与实验之间的比较以及微观机理层面的分析,论证了磁信号峰-谷梯度Kp-v作为磁特征参量,具有表征低周疲劳下焊接钢构件累积延性损伤的潜在可能。
4 结论本文针对焊接试件因应力集中所致的非均匀磁化问题,在既有理论模型的基础上,改进了模拟方法,实现了低周疲劳下V形坡口焊接试件的力-磁耦合有限元仿真。同时,对Q345qC钢焊接试件进行低周疲劳实验,提取不同加载周期下试件表面的金属磁记忆信号。对比实验及模拟结果,研究了磁特征参量与疲劳损伤的相关性,分析得到如下结论。
1) 磁信号峰-谷梯度Kp-v随累积塑性损伤D的增大呈指数递减,验证了Kp-v具有反映低周疲劳下钢材的累积塑性损伤程度的潜在可能。
2) 不同损伤程度下磁信号峰-谷梯度值Kp-v的模拟值与理论值吻合较好,表明所提出的有限元模拟方法可较为准确地描述V形坡口焊接试件HSF(z)信号随塑性循环载荷的变化关系,其可为提高金属磁记忆检测的量化程度提供理论依据。
3) 建立并验证了磁信号峰-谷梯度Kp-v与累积塑性损伤D之间的量化关系,其为低周疲劳下焊接试件塑性损伤的直接评估提供了可能。然而,材料属性、几何尺寸、荷载类型等因素对Kp-v-D关系曲线的影响仍不可忽略,需要进一步的理论和实验研究以完善量化模型。
| [1] |
MUIN S, ASTANEH-ASL A, TOPKAYA C. The response of tall buildings to far-field earthquakes and the case of a 49-story steel building[J]. International Journal of Earthquake and Impact Engineering, 2020, 3(1): 15-39. DOI:10.1504/IJEIE.2020.105378 |
| [2] |
ZENG Qingpei, WANG Xiangchao, WANG Jianting. Influence of the quality factor on simulated seismic waves: A case study of the 1994 Northridge earthquake[J]. Earthquake Science, 2022, 35(5): 329-342. DOI:10.1016/j.eqs.2022.10.008 |
| [3] |
刘洪波, 谢礼立, 邵永松. 钢框架结构的震害及其原因[J]. 世界地震工程, 2006, 22(4): 47-51. LIU Hongbo, XIE Lili, SHAO Yongsong. The earthquake damage of steel frame buildings and the causes of brittle fracture[J]. World Earthquake Engineering, 2006, 22(4): 47-51. DOI:10.3969/j.issn.1007-6069.2006.04.009 |
| [4] |
孙楚津, 陆新征, 程庆乐, 等. 多层钢框架结构的区域震害模拟多自由度模型[J]. 防灾减灾工程学报, 2020, 40(5): 749-756. SUN Chujin, LU Xinzheng, CHENG Qingle, et al. A multi-degree-of-freedom model for regional seismic damage simulation of multi-story steel frame structures[J]. Journal of Disaster Prevention and Mitigation Engineering, 2020, 40(5): 749-756. DOI:10.13409/j.cnki.jdpme.2020.05.009 |
| [5] |
DUBOV A A. A study of metal properties using the method of magnetic memory[J]. Metal Science and Heat Treatment, 1997, 39(9): 401-405. DOI:10.1007/BF02469065 |
| [6] |
DUBOV A A. Development of a metal magnetic memory method[J]. Chemical and Petroleum Engineering, 2012, 47(11-12): 837-839. DOI:10.1007/s10556-012-9559-6 |
| [7] |
WANG Huipeng, DONG Lihong, WANG Haidou, et al. Effect of tensile stress on metal magnetic memory signals during on-line measurement in ferromagnetic steel[J]. NDT & E International, 2021, 117: 102378. DOI:10.1016/j.ndteint.2020.102378 |
| [8] |
XU Kunshan, YANG Ke, LIU Jie, et al. Investigation of magnetic memory signal of propagation of buried crack under applied load[J]. Research in Nondestructive Evaluation, 2021, 32(1): 1-9. DOI:10.1080/09349847.2020.1817640 |
| [9] |
SU Sanqing, YANG Yiyi, WANG Wei, et al. Crack propagation characterization and statistical evaluation of fatigue life for locally corroded bridge steel based on metal magnetic memory method[J]. Journal of Magnetism and Magnetic Materials, 2021, 536: 168136. DOI:10.1016/j.jmmm.2021.168136 |
| [10] |
LENG Jiancheng, XU Minqing, XU Mingxiu, et al. Magnetic field variation induced by cyclic bending stress[J]. NDT & E International, 2009, 42(5): 410-414. DOI:10.1016/j.ndteint.2009.01.008 |
| [11] |
HUANG Haihong, JIANG Shilin, LIU Rujun, et al. Investigation of magnetic memory signals induced by dynamic bending load in fatigue crack propagation process of structural steel[J]. Journal of Nondestructive Evaluation, 2014, 33(3): 407-412. DOI:10.1007/s10921-014-0235-y |
| [12] |
LIU Bin, ZENG Zhihao, WANG Huipeng. Study on the early fatigue damage evaluation of high strength steel by using three components of metal magnetic memory signal[J]. NDT & E International, 2021, 117: 102380. DOI:10.1016/j.ndteint.2020.102380 |
| [13] |
ZHANG Dawei, HUANG Wenqiang, ZHANG Jun, et al. Theoretical and experimental investigation on the magnetomechanical effect of steel bars subjected to cyclic load[J]. Journal of Magnetism and Magnetic Materials, 2020, 514: 167129. DOI:10.1016/j.jmmm.2020.167129 |
| [14] |
SUCHOCKI C, KOWALEWSKI Z. A new method for identification of cyclic plasticity model parameters[J]. Archives of Civil and Mechanical Engineering, 2022, 22: 69. DOI:10.1007/s43452-022-00388-7 |
| [15] |
LIU Qipeng, JIANG Guanglong, GAO Yuehua, et al. Development of improved Manson-Coffin model considering the effect of yield stress under asymmetrical cyclic loading[J]. Journal of Mechanical Science and Technology, 2021, 35(12): 5415-5424. DOI:10.1007/s12206-021-1112-0 |
| [16] |
MA Xiaoping, SU Sanqing, WANG Wei, et al. Experimental and theoretical analysis of the correlation between cumulative plastic damage and SMFL of structural steel under low cycle fatigue[J]. Journal of Magnetism and Magnetic Materials, 2021, 538: 168292. DOI:10.1016/j.jmmm.2021.168292 |
| [17] |
SU Sanqing, MA Xiaoping, WANG Wei, et al. Quantitative evaluation of cumulative plastic damage for ferromagnetic steel under low cycle fatigue based on magnetic memory method[J]. Strain, 2021, 57(3): e12379. DOI:10.1111/str.12379 |
| [18] |
中国国家标准化管理委员会. 气体保护电弧焊用碳钢、低合金钢焊丝: GB/T 8110—2008[S]. 北京: 中国标准出版社, 2008.
|
| [19] |
中国国家标准化管理委员会. 金属材料轴向等幅低循环疲劳试验方法: GB/T 15248—2008[S]. 北京: 中国标准出版社, 2008.
|
| [20] |
廖燕华, 谢旭, 唐站站. Q345qC钢及焊接接头低周疲劳性能与断裂机理[J]. 浙江大学学报(工学版), 2018, 52(1): 73-81. LIAO Yanhua, XIE Xu, TANG Zhanzhan. Low cycle fatigue properties and fracture mechanism of Q345qC steel and its welded joint[J]. Journal of Zhejiang University (Engineering Science), 2018, 52(1): 73-81. DOI:10.3785/j.issn.1008-973X.2018.01.011 |
| [21] |
石永久, 王萌, 王元清. 循环荷载作用下结构钢材本构关系试验研究[J]. 建筑材料学报, 2012, 15(3): 293-300. SHI Yongjiu, WANG Meng, WANG Yuanqing. Experimental study of structural steel constitutive relationship under cyclic loading[J]. Journal of Building Materials, 2012, 15(3): 293-300. DOI:10.3969/j.issn.1007-9629.2012.03.001 |
| [22] |
LENG Jiancheng, LIU Yang, ZHOU Guoqiang, et al. Metal magnetic memory signal response to plastic deformation of low carbon steel[J]. NDT & E International, 2013, 55: 42-46. DOI:10.1016/j.ndteint.2013.01.005 |
| [23] |
SABLIK M J, YONAMINE T, LANDGRAF F J G. Modeling plastic deformation effects in steel on hysteresis loops with the same maximum flux density[J]. IEEE Transactions on Magnetics, 2004, 40(5): 3219-3226. DOI:10.1109/TMAG.2004.832763 |
| [24] |
WANG Zhengdao, DENG Bo, YAO Kai. Physical model of plastic deformation on magnetization in ferromagnetic materials[J]. Journal of Applied Physics, 2011, 109(8): 83928. DOI:10.1063/1.3574923 |
| [25] |
LENG Jiancheng, XU Minqing, ZHOU Guoqiang, et al. Effect of initial remanent states on the variation of magnetic memory signals[J]. NDT & E International, 2012, 52: 23-27. DOI:10.1016/j.ndteint.2012.08.009 |
| [26] |
XUE Liang. A unified expression for low cycle fatigue and extremely low cycle fatigue and its implication for monotonic loading[J]. International Journal of Fatigue, 2008, 30(10-11): 1691-1698. DOI:10.1016/j.ijfatigue.2008.03.004 |
| [27] |
HUANG H L. A study of dislocation evolution in polycrystalline copper during low cycle fatigue at low strain amplitudes[J]. Materials Science and Engineering: A, 2003, 342(1-2): 38-43. DOI:10.1016/S0921-5093(02)00312-X |
| [28] |
SORNETTE D, MAGNIN T, BRECHET Y. The physical origin of the Coffin-Manson law in low-cycle fatigue[J]. Europhysics Letters, 2007, 20(5): 433-438. DOI:10.1209/0295-5075/20/5/009 |
 2024, Vol. 32
2024, Vol. 32


