- ScholarOne
- 登录
Please submit manuscripts in either of the following two submission systems
ScholarOne Manuscripts
勤云稿件系统
Search by Issue
Search by Keywords
News & AnnouncementMORE
- 【03-29】2015 Outstanding Reviewers
- 【03-27】2014 Outstanding Reviewers
- 【02-18】2013 Outstanding Reviewers
- 【12-29】The First Outstanding Reviewers
- 【05-04】Copyright Transfer Agreement
- 【04-04】To authors
Supervised by Ministry of Industry and Information Technology of The People's Republic of China Sponsored by Harbin Institute of Technology Editor-in-chief Yu Zhou ISSNISSN 1005-9113 CNCN 23-1378/T


|
||||||||||||||||||||||||||||||


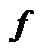 (
( 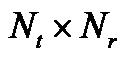 ),
), 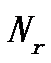 是检波器坐标样本数,
是检波器坐标样本数, 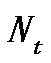 是时间轴坐标样本数,设
是时间轴坐标样本数,设 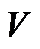 是向量化算子,
是向量化算子, 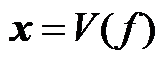 ,
, 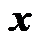 为(
为( 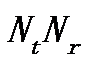 )向量。欠采样地震资料设为
)向量。欠采样地震资料设为 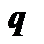 (
( 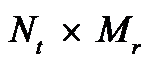 ),
), 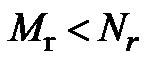 ,向量化后
,向量化后 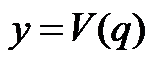 ,
,  为(
为( 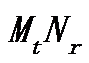 )维向量,则欠采样地震数据可以表示为式(1):
)维向量,则欠采样地震数据可以表示为式(1):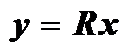 (1)
(1)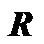 是一个二元采样矩阵,从
是一个二元采样矩阵,从 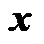 采样得到
采样得到 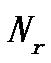 道抽取
道抽取 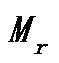 道数据。因为
道数据。因为 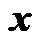 ,设地震资料
,设地震资料  在变换域
在变换域 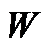 下系数为
下系数为 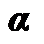 ,有
,有  ,
, 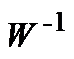 是
是 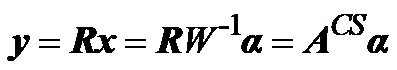 (2)
(2)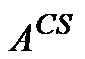 满足有限等距性质的前提下,为通过
满足有限等距性质的前提下,为通过  范数优化问题如式(3)。
范数优化问题如式(3)。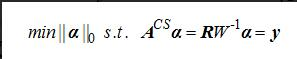 (3)
(3)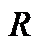 和
和 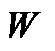 不相关的条件下,可以转为求解一个等价的、更加简单的
不相关的条件下,可以转为求解一个等价的、更加简单的 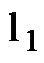 范数优化问题如式(4)。
范数优化问题如式(4)。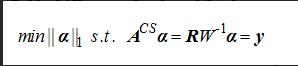 (4)
(4)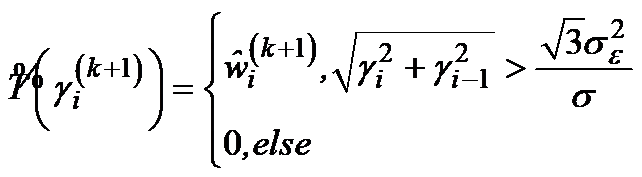 (5)
(5)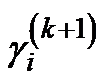 表示第
表示第 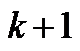 次迭代,地震缺失数据在Curvelet域尺度为
次迭代,地震缺失数据在Curvelet域尺度为 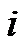 的系数,
的系数, 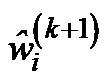 表示地震完整数据在Curvelet域尺度为
表示地震完整数据在Curvelet域尺度为 