欢迎访问《材料科学与工艺》编辑部网站！

基于微观形貌的逆偏析形成机理的数值模拟分析

doi: 10.11951/j.issn.1005-0299.20230075

张宇，朱宝丰，张士杰，张冰，张思雨，李日

河北工业大学材料科学与工程学院，天津市 300401

基金项目: 国家自然科学基金资助项目(51975182)

详细信息

作者简介

张宇(1997—)，男，硕士研究生.

通讯作者

李日，E-mail: sdzllr@163.com

中图分类号: TG111.4

文献标识码: A

文章编号: 1005-0299(2025)01-0031-10

Numerical simulation study on the formation mechanism of reverse segregation based on microscopic morphology

ZHANG Yu ， ZHU Baofeng ， ZHANG Shijie ， ZHANG Bing ， ZHANG Siyu ， LI Ri

School of Materials Science and Engineering, Hebei University of Technology, Tianjin 300401 , China

摘要

铸件中逆偏析的存在会显著降低铸件的力学性能和切削加工性能，因此研究逆偏析的形成机理具有重要意义。采用微观尺度的元胞自动机(CA)耦合格子玻尔兹曼方法(LBM)的模型，以Al-4.7wt.%Cu合金为例，分别模拟了计算域的全域柱状晶凝固、柱状晶向等轴晶转变(CET)的凝固和全域等轴晶凝固，并且分析了逆偏析的形成机理。研究发现，计算域边界较低的温度以及柱状晶发达的二次枝晶对含有溶质的熔体的分割阻碍是逆偏析形成的主要原因。计算域边界降温速度越快，逆偏析程度就越大；柱状晶对含有溶质的熔体的分割阻碍作用比中心等轴晶要大，凝固组织全部为柱状晶时，逆偏析最为严重，凝固组织同时含有柱状晶和等轴晶时，逆偏析次之，凝固组织全部为等轴晶时逆偏析最轻。计算域中心溶液受重力影响沿流场流向计算域底部的枝晶间隙，使计算域底部逆偏析程度大于其他部分。在铸锭凝固过程中可以考虑增加机械或者电磁搅拌、增大等轴晶区面积或者降低散热速率来降低逆偏析对铸锭的不利影响。

关键词

逆偏析 / 元胞自动机 / 格子玻尔兹曼 / 微观形貌 / 数值模拟 / Al-Cu合金

Abstract

The existence of inverse segregation in castings tends to significantly reduce the mechanical properties and machinability of castings and heightens the importance of investigating the formation mechanism of inverse segregation. A microscale cellular automata (CA)-coupled lattice Boltzmann method (LBM) model is established. The global columnar solidification, columnar to equiaxed transition (CET) solidification and global equiaxed solidification are simulated to analyze the formation mechanism of inverse segregation. The main reasons for the formation of inverse segregation are the lower temperature at the computational domain boundary and the separation of the solute-containing melt by secondary dendrites with the formed columnar crystals. A faster cooling rate at the computational domain boundary correlates to a greater degree of inversion. The inverse segregation of the computational domain with global columnar solidification is the most severe, followed with columnar to equiaxed transformation solidification, and the inverse segregation with global equiaxed solidification is the least severe. The reverse segregation at the bottom of the computational domain caused by gravity is greater than that of the rest.

Keywords

inverse segregation / cellular automata / Lattice Boltzmann / micromorphology / numerical simulation / Al-Cu alloy

1 计算模型 1.1 元胞自动机（CA）模型 1.1.1 形核模型 1.1.2 生长模型 1.1.3 捕获模型 1.2 格子玻尔兹曼（LBM）模型 2 模型验证 3 逆偏析的计算结果讨论 3.1 计算模型及模拟条件 3.2 全域柱状晶凝固的逆偏析计算分析 3.3 凝固组织为柱状晶和等轴晶的逆偏析计算分析 3.4 全域等轴晶凝固的逆偏析分析 4 讨论 5 结论

逆偏析是宏观偏析的一种，与正偏析相反，逆偏析表现为铸件表面层的溶质浓度比内部溶质浓度高。逆偏析的存在会对铸件的力学性能及后续加工产生不利影响，因此研究其形成机制对防止或削弱逆偏析的出现有重要意义。在对逆偏析的实验研究中，余辉辉等^[1]发现电磁搅拌可将粗大的树枝晶转变为等轴晶，改善高锡青铜的逆偏析。El-bealy^[2]发现Al-4.5wt.%Cu合金柱状晶之间的宽度对逆偏析有重要影响，并且发现Cu受重力影响在铸锭底部溶质浓度较高。

由于一般合金铸锭或铸件的凝固过程是不透明的，实验研究难以展现宏观偏析的动态形成过程^[3-6]，因此数值模拟就成为一种研究宏观偏析动态形成过程的重要方法。逆偏析的早期研究始于解析模型，最近，Vynnycky^[7]对传统的溶质再分配方程进行了扩展，可用于固相中溶质扩散不可忽略的情况下以及凝固模式为等轴树枝晶时。但是解析模型只适合于定性的模拟计算，不能模拟逆偏析形成过程中的组织形貌。

为了克服解析模型存在的问题，随着模拟技术的发展，又出现了数值模型。近期，Chen等^[8]建立了任意拉格朗日-欧拉（ALE）模型，该模型考虑了溶质对流和凝固收缩，成功地预测逆偏析。Yu等^[9]用相场法模拟了双辊铸轧过程中的逆偏析现象，并且发现逆偏析影响了材料的伸长率和抗拉强度。Sabatini等^[10]在非稳态条件下，分别模拟计算了合金的冷却曲线和二次枝晶臂间距，并且讨论了逆偏析现象及与冷却速度和溶质浓度的关系。

前文介绍的数值模型均未涉及到微观形貌，而从偏析形成的机制来说，微观组织形貌对逆偏析有重要影响^[11-12]。为此，本文拟采用元胞自动机耦合格子玻尔兹曼方法（CA-LBM）来研究逆偏析。与其他模拟计算方法相比，元胞自动机（Cellular Automata，CA）方法可以更好地模拟微观组织的形貌^[13-15]，格子玻尔兹曼（Lattice Boltzmann Method，LBM）方法在处理枝晶间的流动时更具有优势^[16-18]，因此该模型可以更加准确地预测宏观偏析。

本文建立了CA耦合 LBM 模型，基于微观组织尺度，同时考虑温度场、溶质场以及流场的耦合传输，以 Al-4.7wt.%Cu合金为例研究逆偏析的动态形成机制。

1 计算模型

采用CA-LBM耦合模型来进行逆偏析数值模拟，其中，用 CA 方法计算微观组织的形核、生长和捕获过程，用 LBM 计算凝固过程中的流场、溶质场和温度场。

1.1 元胞自动机（CA）模型

1.1.1 形核模型

本文使用的形核模型是基于Rappaz^[19]提出的连续形核模型。

1.1.2 生长模型

CA方法中，对计算域进行网格剖分，一个网格就是一个元胞，每个元胞可能的状态有3种：液态、界面和固态。以元胞中的固相率f_s作为划分标准，当 f_s=0时，为液态；当f_s=1.0 时，为固态；当0＜ f_s＜1.0时，为界面元胞。对每个元胞同时赋予如下参数：温度、浓度、速度、固相率。初始时，计算域中的所有元胞均为液态，当达到形核条件时随即转变为界面元胞，当固相率生长为1.0 时，元胞转变为固态元胞。采用朱鸣芳等^[20]提出的溶质扩散模型计算枝晶的生长，枝晶生长的驱动力为固/液界面的平衡溶质浓度与液相实际溶质浓度之差。

根据界面处的热力学平衡条件，界面平衡温度T^*为

T^{*} = T_{1}^{e q} + (C_{1}^{*} - C_{0}) m_{1} - Γ K f (φ, θ_{0})

(1)

式中：T^eq₁为初始溶质浓度C₀处的液相线温度；C^*₁为界面平衡溶质浓度；m₁为液相线斜率；Γ为吉布斯-汤普森系数；K为固液界面处曲率^[21]；f（φ，θ₀）为考虑界面张力的各向异性函数。其中K的表达式为

\begin{matrix} K = {[\frac{\partial f_{s}^{2}}{\partial x} + \frac{\partial f_{s}^{2}}{\partial y}]}^{- \frac{3}{2}} \times [2 \frac{\partial f_{s}}{\partial x} \frac{\partial f_{s}}{\partial y} \frac{\partial^{2} f_{s}}{\partial y^{2}} - \\ {(\frac{\partial f_{s}}{\partial x})}^{2} \frac{\partial^{2} f_{s}}{\partial y^{2}} - {(\frac{\partial f_{s}}{\partial y})}^{2} \frac{\partial^{2} f_{s}}{\partial x^{2}}] \end{matrix}

(2)

其中f_s为元胞的固相率。

f（φ，θ₀）的表达式为^[22]

f (φ, θ_{0}) = 1 - δ c o s [4 (θ, θ_{0})]

(3)

式中：θ₀为择优生长方向与x轴的夹角；φ为界面法线方向与 x 轴的生长夹角；δ为各向异性系数。

由此可得界面平衡溶质浓度C^*₁为

C_{1}^{*} = C_{0} + (T_{1}^{*} - T_{1}^{e q}) / m

(4)

式中：C₀为初始溶质浓度；T^*₁为界面温度；T^eq₁为初始溶质浓度的平衡液相线温度；m为相图的液相线斜率。界面元胞的固相率增加量为

Δ f_{s} = (C_{1}^{*} - C_{1}) / [C_{1}^{*} (1 - k)]

(5)

式中：C₁为液相溶质浓度；k为平衡分配系数。

1.1.3 捕获模型

界面元胞完全凝固成为固相元胞随即捕获周围的液相元胞，使之变为界面元胞。通常采用的捕获方式有两种类型，如图1所示，分别为 Von-Neumann（四邻居捕获）类型和 Moore（八邻居捕获）。本文采用八邻居捕获方式。

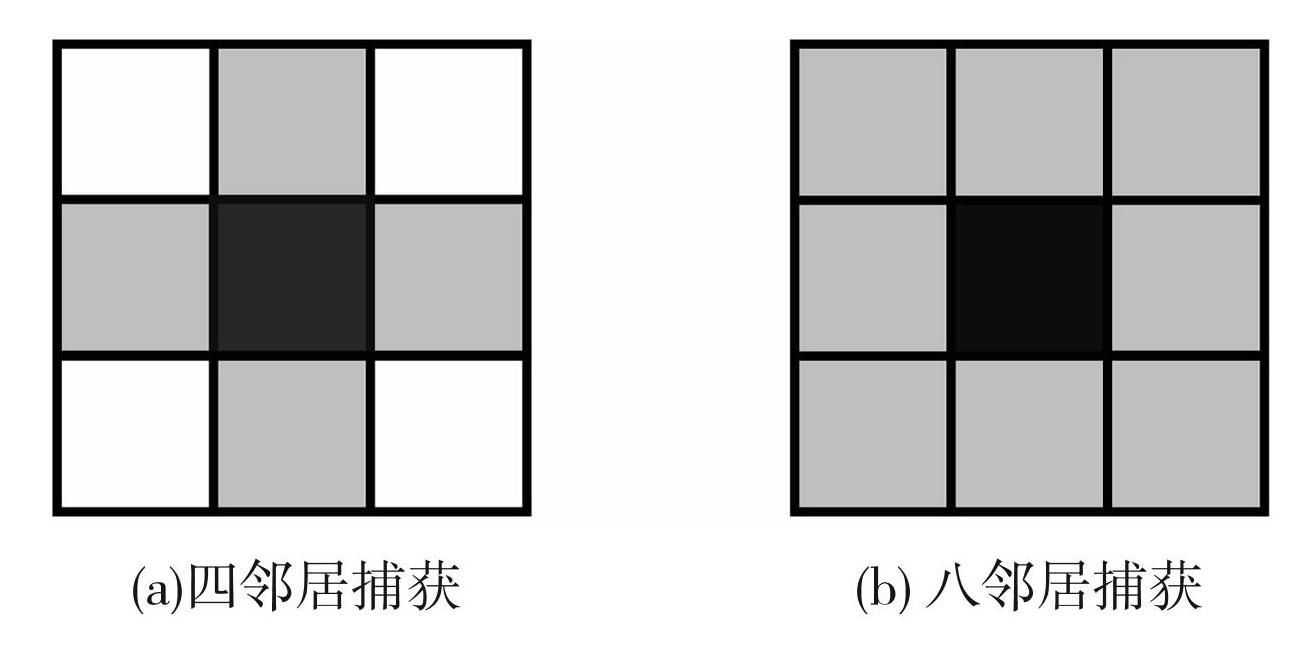
图1捕获方式

Fig.1Capture rule: (a) Von-Neumann; (b) Moore

1.2 格子玻尔兹曼（LBM）模型

LBM方法不考虑单个粒子的运动，而是将所有粒子的运动视为一个整体，用分布函数表示，然后利用方程的离散解来描述虚拟粒子分布函数的演化，通过分布函数计算宏观变量。本文采用单松弛时间的D2Q9双分布函数模型，流场、温度场和浓度场的玻尔兹曼方程为：

\begin{matrix} f_{i} (x + e_{i} Δ t, t + Δ t) - f_{i} (x, t) = \\ \frac{1}{τ_{f}} [f_{i}^{e q} (x, t) - f (x, t)] + F_{i} (x, t) \end{matrix}

(6)

\begin{matrix} g_{i} (x + e_{i} Δ t, t + Δ t) - g_{i} (x, t) = \\ \frac{1}{τ_{t}} [g_{i}^{e q} (x, t) - g_{i} (x, t)] + G_{i} (x, t) \end{matrix}

(7)

\begin{matrix} m_{i} (x + e_{i} Δ t, t + Δ t) - m_{i} (x, t) = \\ \frac{1}{τ_{c}} [m_{i}^{e q} (x, t) - m_{i} (x, t)] + M_{i} (x, t) \end{matrix}

(8)

式中：x为粒子的位置；t为粒子的时间；Δt为时间步长；F_i（x，t）为外力项；G_i（x，t）为潜热引起的潜热源项；M_i（x，t）为溶质再分布溶质源项；τ_f、τ_t、τ_c分别为流场、温度场和浓度场的松弛时间；f_i（x，t）、g_i（x，t）、m_i（x，t）分别为流场、温度场、溶质场分布函数，分别表示在i方向上，一个粒子在时间t出现在位置x的概率，粒子在i方向的离散速度可以表示为

e_{i} = \{\begin{matrix} (0,0), i = 0 \\ c (c o s \frac{(i - 1) π}{2}, s i n \frac{(i - 1) π}{2}), \\ i = 1,2, 3,4 \\ \sqrt{2} c (c o s \frac{(2 i - 1) π}{2}, s i n \frac{(2 i - 1) π}{2}), \\ i = 5,6, 7,8 \end{matrix}

(9)

其中格子速度c=Δx/Δt，Δx为网格边长，Δt为计算时间步长，本文中Δt = 10^-6 s。弛豫时间与宏观扩散系数的关系为：

τ_{f} = 3 \frac{Δ t}{Δ x^{2}} v + 0.5

(10)

τ_{t} = 3 \frac{Δ t}{Δ x^{2}} α + 0.5

(11)

τ_{c} = 3 \frac{Δ t}{Δ x^{2}} D + 0.5

(12)

式中：υ为流体动力粘度；α为热扩散系数；D为溶质扩散系数。其中α表达为

α = \frac{λ}{ρ C_{p}}

(13)

式中：λ为热导率；ρ为密度；C_p为比热容。

流场、温度场和溶质场的平衡分布函数可表示为：

\begin{matrix} f_{i}^{e q} (x, t) = ω_{i} ρ [1 + 3 e_{i} \cdot u / c^{2} + 9 {(e_{i} \cdot u)}^{2} / 2 c^{4} - \\ 3 (u \cdot u) / 2 c^{2}] \end{matrix}

(14)

\begin{matrix} g_{i}^{e q} (x, t) = ω_{i} T [1 + 3 e_{i} \cdot u / c^{2} + 9 {(e_{i} \cdot u)}^{2} / 2 c^{4} - \\ 3 (u \cdot u) / 2 c^{2}] \end{matrix}

(15)

\begin{matrix} m_{i}^{e q} (x, t) = ω_{i} C [1 + 3 e_{i} \cdot u / c^{2} + 9 {(e_{i} \cdot u)}^{2} / 2 c^{4} - \\ 3 (u \cdot u) / 2 c^{2}] \end{matrix}

(16)

式中：ω_i为每个方向的加权系数，即ω₀=4/9，ω_1-4=1/9，ω_5-8=1/36；c为格子速度。

流场中的外力项为^[23]

F_{i} (x, t) = (1 - \frac{1}{2 τ_{f}}) ω_{i} (3 \frac{e_{i} - u}{c^{2}} + 9 \frac{e_{i} \cdot u}{c^{4}}) F Δ t

(17)

其中F是由温度和溶质变化引起的体积力，由下式计算得出^[24]

F = g ρ_{0} β_{T} (T - T_{0}) + g ρ_{0} β_{C} (C - C_{0})

(18)

式中：g为重力加速度；β_T和β_C分别为温度膨胀系数和溶质膨胀系数。

由枝晶生长释放的潜热引起的潜热源项和溶质再分布溶质源项分别为：

G_{i} (x, t) = ω_{i} Δ f_{s} L / C_{p}

(19)

M_{i} (x, t) = ω_{i} C_{l} (1 - k) Δ f_{s}

(20)

式中：L为潜热；C_p为比热容。

流体宏观密度ρ、速度u、温度T、溶质浓度C分别为：

ρ = \sum_{i = 0}^{8} f_{i}

(21)

ρ u = \sum_{i = 0}^{8} e_{i} f_{i}

(22)

T = \sum_{i = 0}^{8} g_{i}

(23)

C = \sum_{i = 0}^{8} m_{i}

(24)

本文的LBM边界条件为：流场的物理边界条件为充分发展边界条件；温度场边界条件为非平衡外推格式；浓度场边界条件为充分发展边界条件；固液边界采用纯反弹格式。

2 模型验证

本文所采用的模型与Zhang^[13]和Liu^[25]的模型相同，已经过验证，属于成熟的模型。以下采用该模型对Al-4.7wt.%Cu合金的定向凝固过程进行模拟计算，凝固方向为从计算域底面向上凝固，以判断该模型在计算逆偏析方面的可靠性，其中Al-4.7wt.%Cu合金的热物性参数^[26-27]如表1所示。

本文选取的定向凝固计算域大小为300×600，每个网格的大小为1 μm×1 μm，初始温度为918 K，底部散热，其它边界绝热。图2为计算结果的溶质分布图，图2中（a）、（b）、（c）对应计算步数分别为5 000、18 000和32 000步。

表1Al-4.7wt.%Cu合金的热物性参数

Table1Physical properties of Al-4.7wt.%Cu alloy

当计算到5 000步（图2（a））时，计算域底部柱状晶竞争生长，18 000步（图2（b））时计算域顶部开始出现中心等轴晶，之后等轴晶沿各自的生长方向生长。由图2（c）可以看到柱状晶向等轴晶转变的过程，也可以看到接近底部附近的明显的逆偏析区域。图3为图2（c）的左右对称轴处（即图2（c）中的黑色虚线）的偏析度分布图，偏析度R为

R = (C - C_{0}) / C_{0}

(25)

式中：C₀为凝固前的初始溶质浓度；C为计算域中实际溶质浓度。当R＞0 时，说明实际溶质浓度比初始溶质浓度高，为正偏析；R＜0 时，说明实际溶质浓度比初始溶质浓度低，为负偏析。R的绝对值越大，说明其偏析程度越大。

图2定向凝固溶质分布图

Fig.2Distribution of solute in directional solidification: (a) 5 000 step； (b) 18 000 step； (c) 32 000 step

图3中忽略了C＜C₀的元胞，因为C＜C₀时为先生长的树枝晶部分，而逆偏析主要出现在树枝晶间隙部分即C＞C₀的部分。本文中之后的研究中同样也忽略了C＜C₀的元胞，后文不再赘述。图3中可以看到明显的逆偏析，下边界部分偏析程度高，远离下边界的区域偏析程度越低。这与Gao等^[28]根据Mehrabian偏析模型计算得到的铝铜合金定向凝固偏析分布图相似，说明用本文模型计算的逆偏析是合理的。

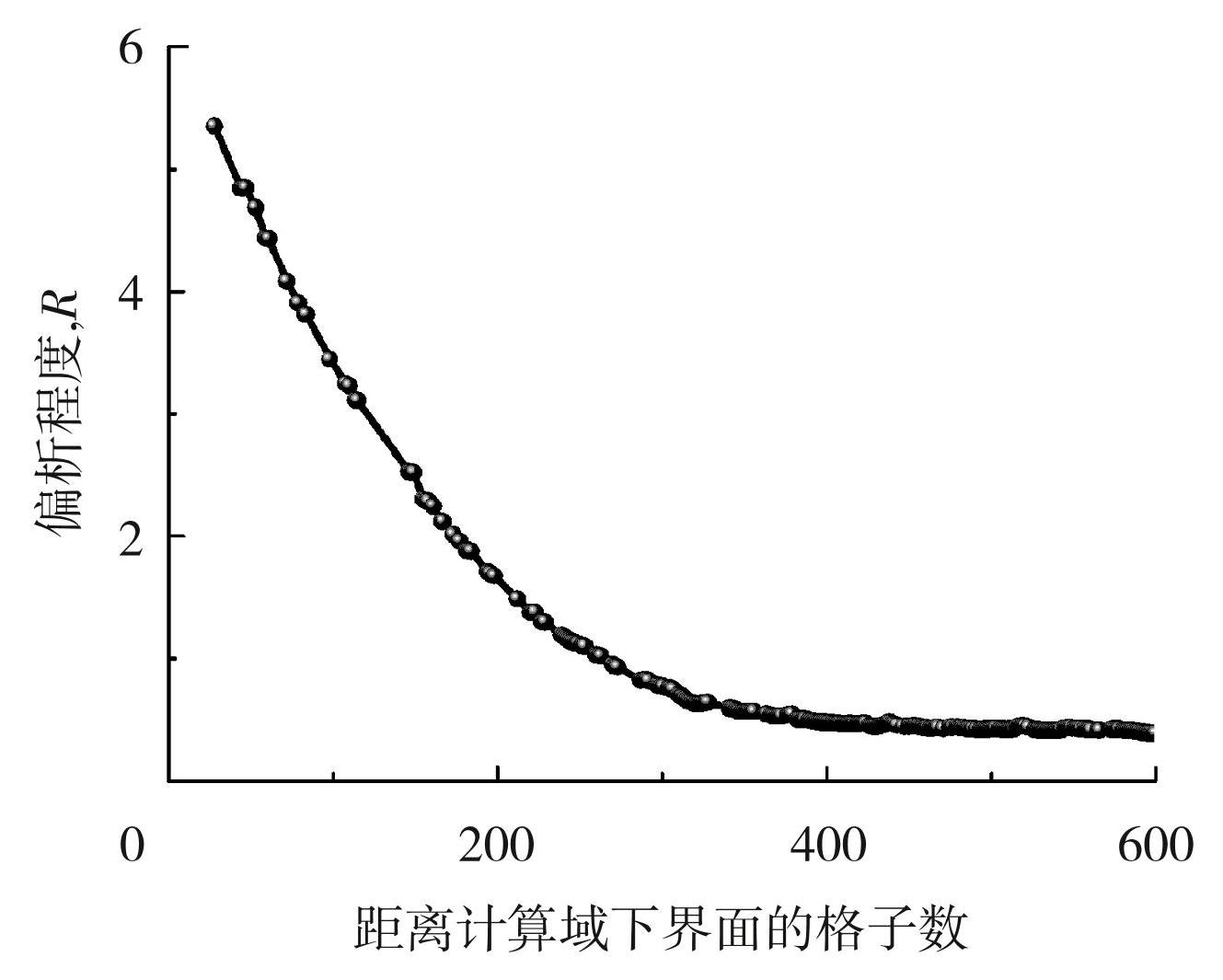
图3计算域左右对称轴处偏析程度分布图

Fig.3The distribution diagram of the degree of segregation at the left and right symmetry axes of the computational domain

3 逆偏析的计算结果讨论

目前普遍认为在以柱状枝晶为主的铸锭中，高溶质浓度的液相沿着柱状枝晶通道反向流动是逆偏析形成的原因，而以等轴晶为主的合金的逆偏析机理仍不清楚^[29]。为了从数值模拟的角度对此问题做出回答，本文拟从如下3个方面展开研究：

1）计算域除表面细晶区外，其余部分均为柱状晶，即计算在全域柱状晶凝固的条件下是否会发生逆偏析的现象，并分析其成因。

2）计算域存在柱状晶向等轴晶转变（CET），即计算既有柱状晶又有等轴晶的情况下是否会发生逆偏析的现象，并分析其成因。

3）计算域内部组织全部为等轴晶，计算是否会发生逆偏析的现象，并分析其成因。

综合上述研究结果，分析总结逆偏析形成机制。

3.1 计算模型及模拟条件

图4为本文选取的计算域模型图，材料为Al-4.7wt.%Cu 合金，其它计算条件如下：

1）划分计算域网格数为400×800，在计算域y=100，y=400以及y=700时3条水平线处根据模拟结果分别分析其偏析程度。

2）熔体初始温度为920 K，顶部边界绝热，下部及左右两侧的传热系数q_w均为700 W/（m²·K），重力加速度g为9.81 m/s²。

3）假定溶质扩散只存在于液相中，忽略溶质在固相中的扩散。

4）不考虑凝固过程中枝晶和熔体的收缩，仅考虑因溶质浓度和温度引起的Boussinesq近似。

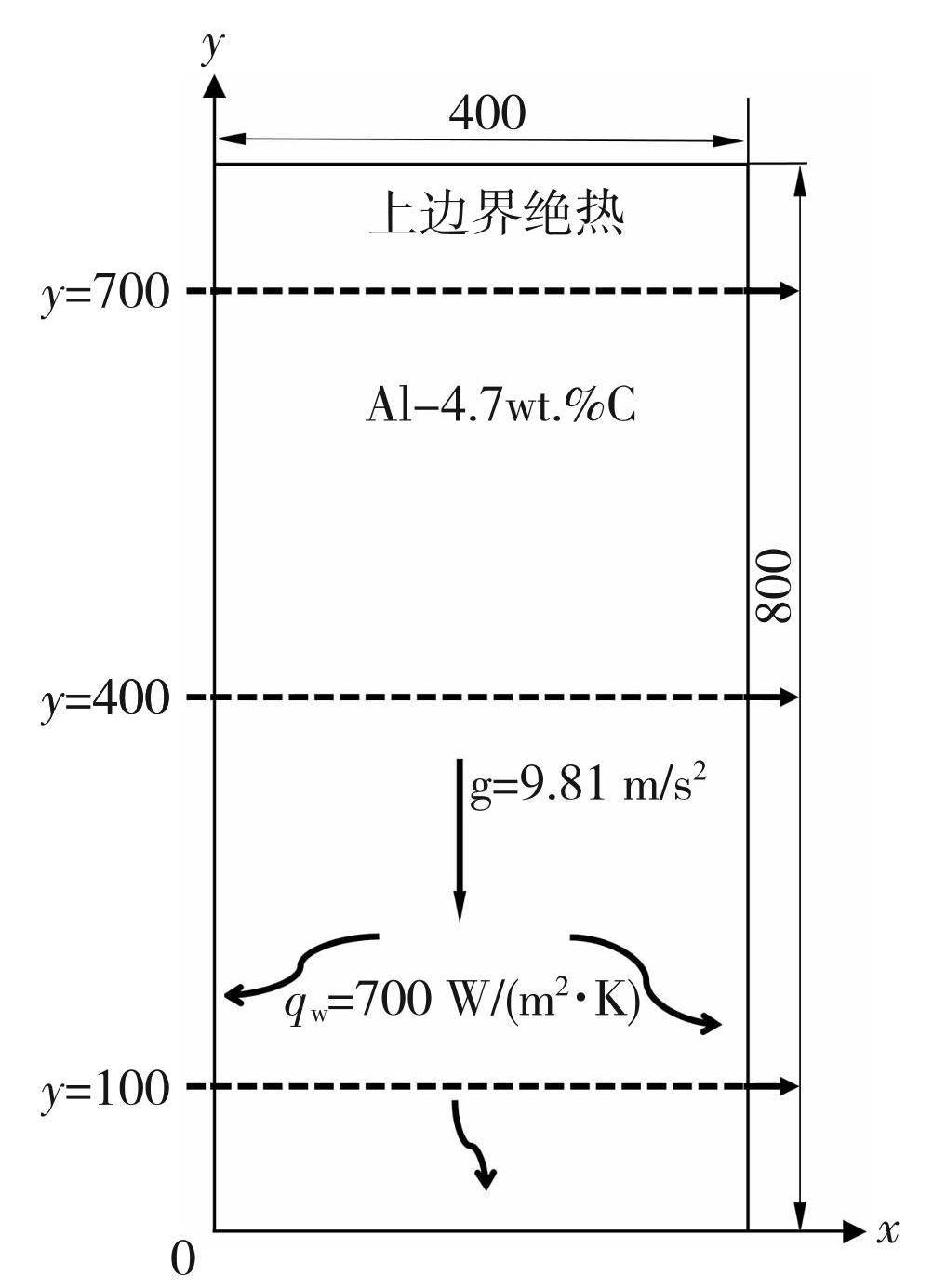
图4凝固初始条件示意图

Fig.4Initial conditions of solidification

3.2 全域柱状晶凝固的逆偏析计算分析

图5为计算域全域柱状晶凝固的微观组织分布，图6为相应的溶质分布图，凝固时的计算步数分别为10 000、13 000和17 000步。

图5全域柱状晶凝固微观组织

Fig.5Microstructure of global columnar solidification: (a) 10 000 step; (b) 13 000 step; (c) 17 000 step

图6全域柱状晶凝固溶质分布图

Fig.6Distribution of solute in global columnar solidification: (a) 10 000 step; (b) 13 000 step; (c) 17 000 step

从形貌图可以看到表面等轴晶区和柱状晶区的竞争生长。由于散热方向为下、左、右3个界面，柱状晶基本沿散热方向的反向生长，柱状晶均有二次枝晶，会对流场的流动和溶质扩散产生阻碍作用。从图6也可以看出典型的逆偏析溶质分布特点：计算域表面部分溶质浓度高，中间部分溶质浓度低。并且，越靠近底部的部分溶质浓度越高，逆偏析程度越明显。

逆偏析形成的原因如下：首先，枝晶在生长过程中会释放溶质到液相中，使溶质在枝晶前沿聚集，而所排出的溶质元素为Cu，使得生长枝晶前沿的熔体密度大于初始熔体密度，这种熔体下沉的倾向要大于横向对流，而且由于柱状晶一次枝晶臂较长，二次枝晶把这些溶质浓度较高的熔体阻隔在柱状枝晶尖端后部，因此难于通过横向对流与中心区域的熔体混合，这就将这些高浓度的熔体阻滞在了柱状晶的后部；其次，如图7（a）所示，凝固时枝晶的生长会把熔体推向中心方向，但是由于二次枝晶的存在，严重阻碍了熔体的流动，使得趋向中心的流动速度非常小。因为本文的模型没有考虑枝晶收缩引起的趋向计算域壁面的流动，如果考虑了这种流动，则趋向中心的流动速度会更小，甚至会发生趋向壁面的流动，但即便是如此，也出现了明显的逆偏析。此外，计算域接近壁面处的温度较低，根据Al-Cu相图（图8），温度越低，溶质Cu的浓度就越高，这是过去关于逆偏析形成原因的分析时没有注意到的。图9为合金在不同冷却速率下的偏析程度对比图，可以看到，冷却速率越快，偏析程度越大，这与本文的分析相符合。计算域边界处温度低，根据Al-Cu相图（图8），温度越低，溶质Cu的浓度就越高。最后，如图7（c）所示，在凝固的枝晶尖端前沿的涡流也会对从枝晶后部流过来的熔体产生阻碍作用，使溶质在枝晶后部的二次枝晶间滞留，这也是逆偏析形成的原因。

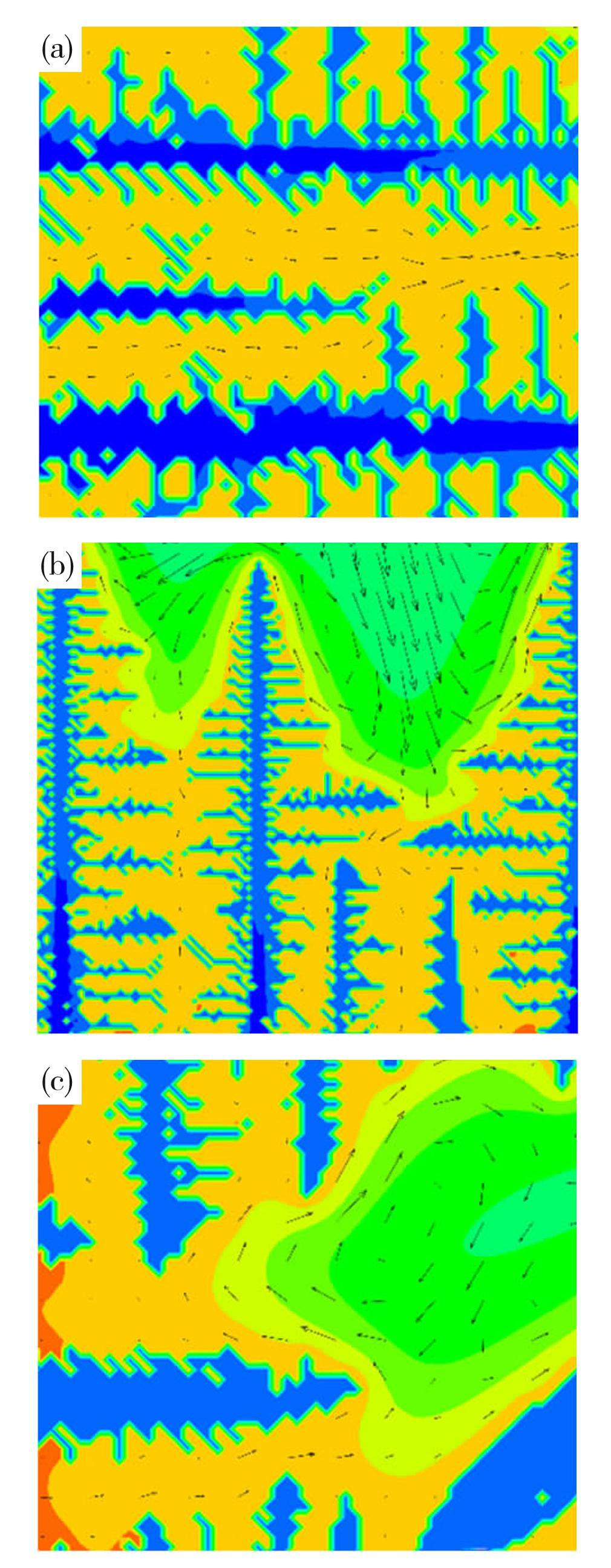
图7Zone-1（a），Zone-2（b），Zone-3（c）的放大图

Fig.7Enlarged view of Zone-1 (a) , Zone-2 (b) and Zone-3 (c)

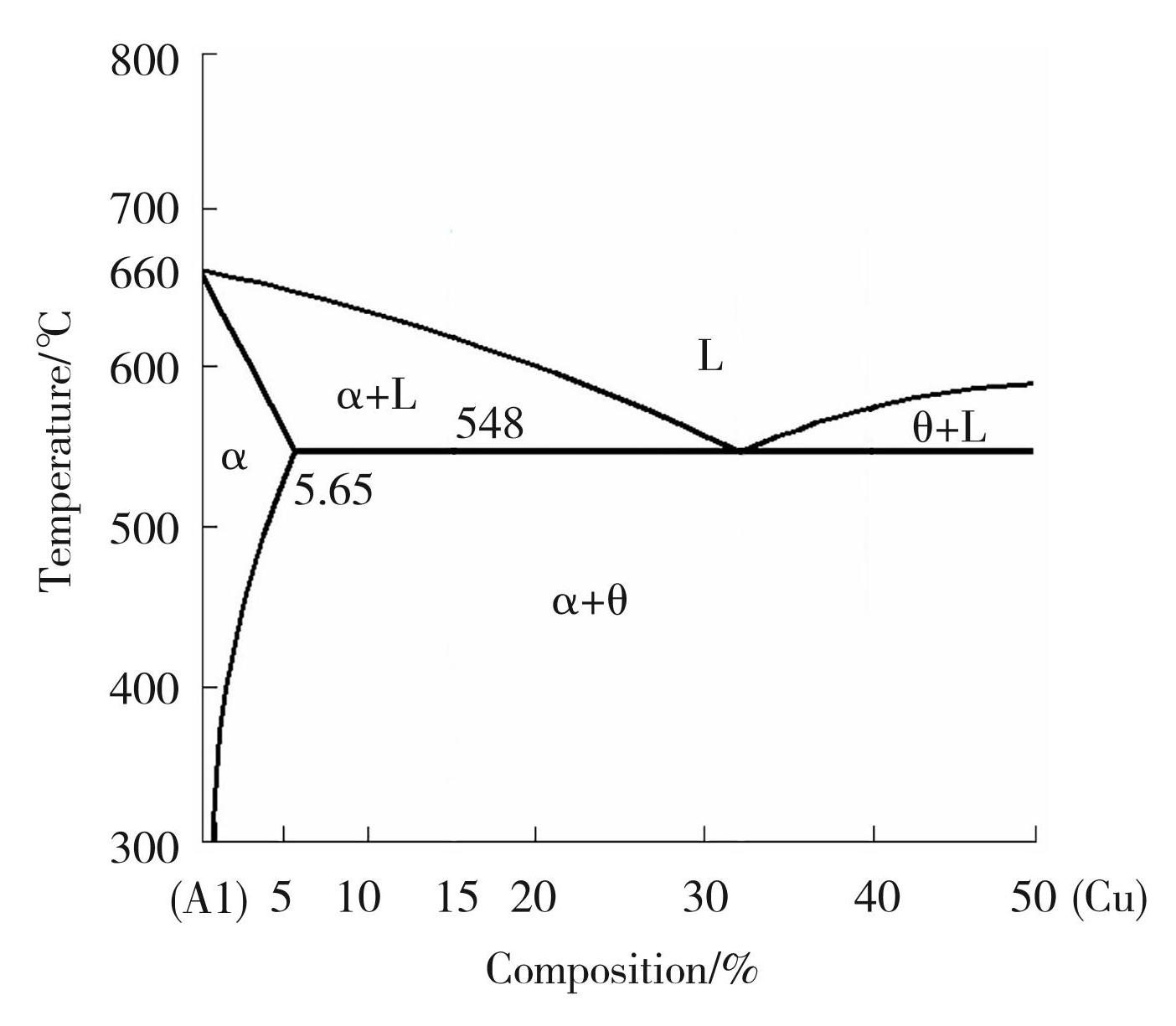
图8Al-Cu相图

Fig.8Aluminum-copper phase diagram

随着柱状枝晶及其二次枝晶的生长，溶质扩散和流场流动的通道越来越长也越来越窄，溶质越来越难以扩散，而且靠近边界的枝晶生长时，继续排出溶质，使枝晶间的溶质浓度不断升高，这就导致了先凝固的表层部分溶质浓度高，从而形成逆偏析。可见，在靠近壁面的凝固区域温度较低，所以更容易形成高浓度的熔体，而越是靠近中心区域的熔体，温度梯度越低，高溶质浓度的熔体形成得越慢，在形成过程中还会发生溶质扩散，并且与其他熔体混合，所以靠近中心区域的熔体浓度反而更低。在计算域下方，在重力作用下，凝固前沿上方的溶质浓度较低的熔体会流向下部枝晶之间，如图7（b）所示，铜的密度比铝大，溶质随流场作用在计算域下方的枝晶间隙积聚。这种现象导致了底部的溶质浓度大，逆偏析程度高，如图10中y=100偏析线所示，即越靠近计算域底部偏析程度越大，3条水平线中，在y = 100的水平线处偏析程度最高。

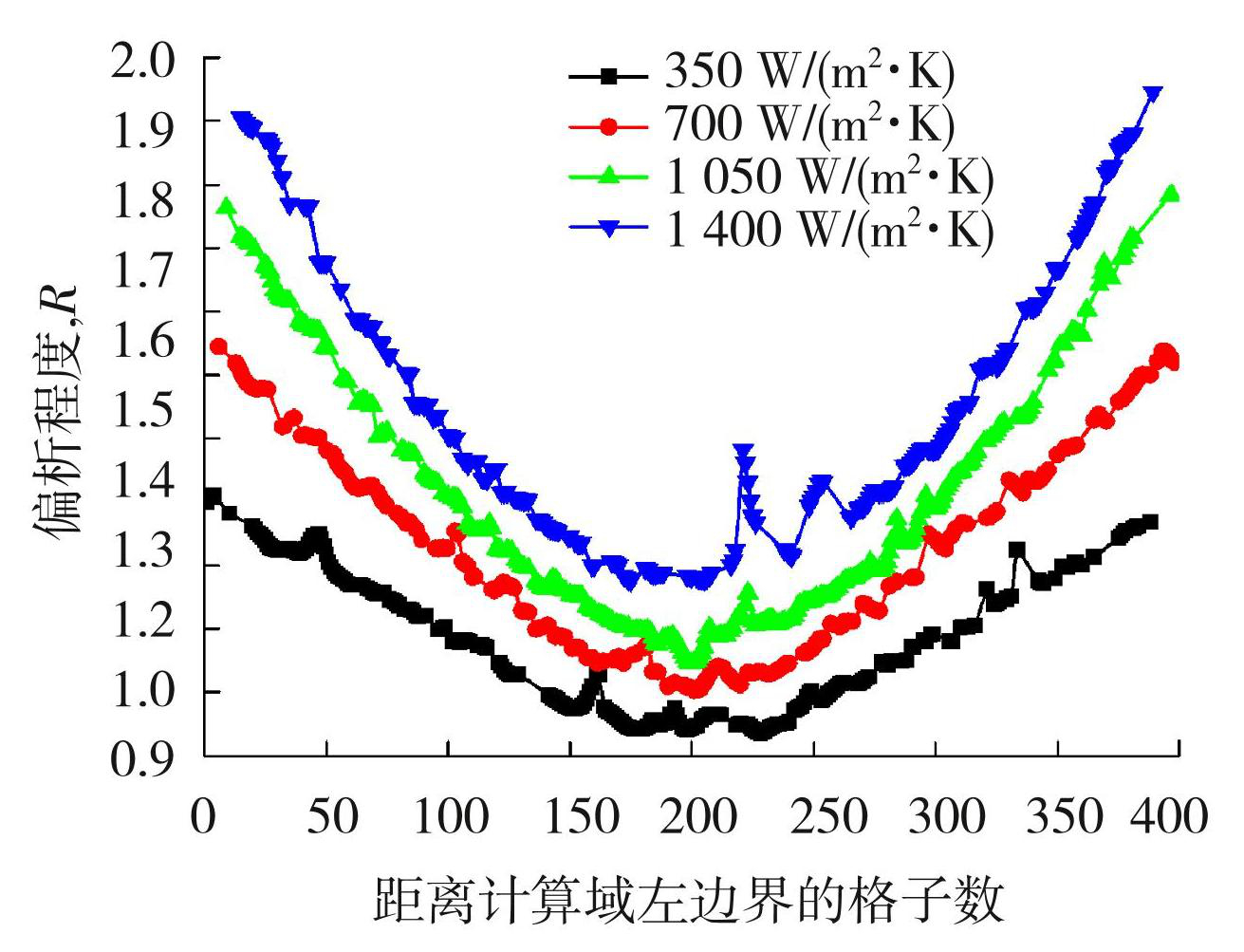
图9在不同冷却速率下凝固的偏析程度对比图

Fig.9Comparison diagram of segregation degree of solidification at different cooling rates

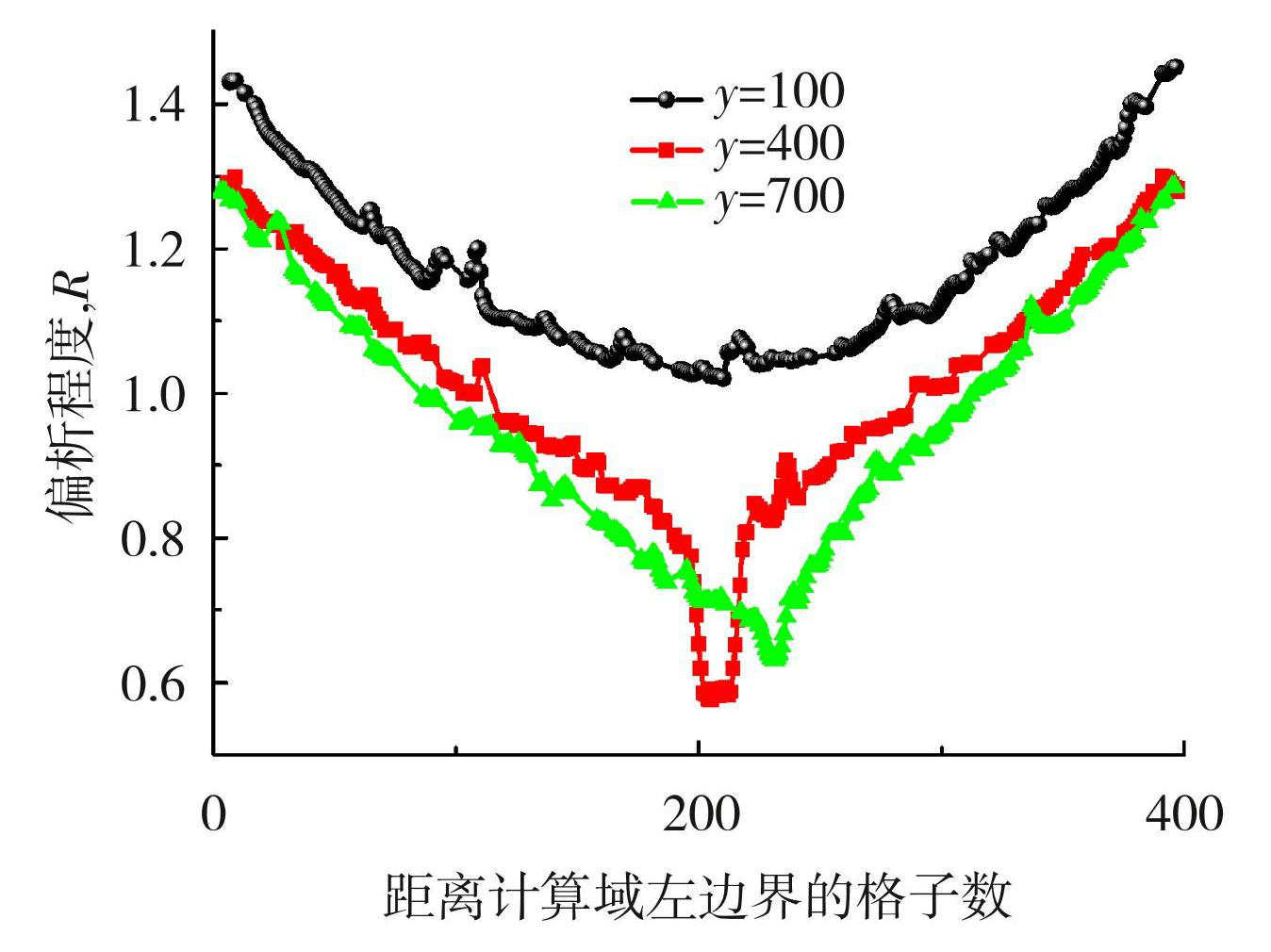
图10全域柱状晶凝固不同水平高度的水平偏析度分布

Fig.10Distribution of horizontal segregation at different levels of global columnar solidification

3.3 凝固组织为柱状晶和等轴晶的逆偏析计算分析

图11和图12给出了溶液以柱状晶向等轴晶转变（CET）的形式凝固时的形貌图和溶质分布图，对应的计算时间步长分别为9 000、11 300和14 000步。图13为计算域不同水平高度的偏析度分布图。可见，当凝固到9 000步时，计算域只有柱状晶，这时的生长情况与全域柱状晶凝固初始相似，此时形成逆偏析的原因与柱状晶相同。

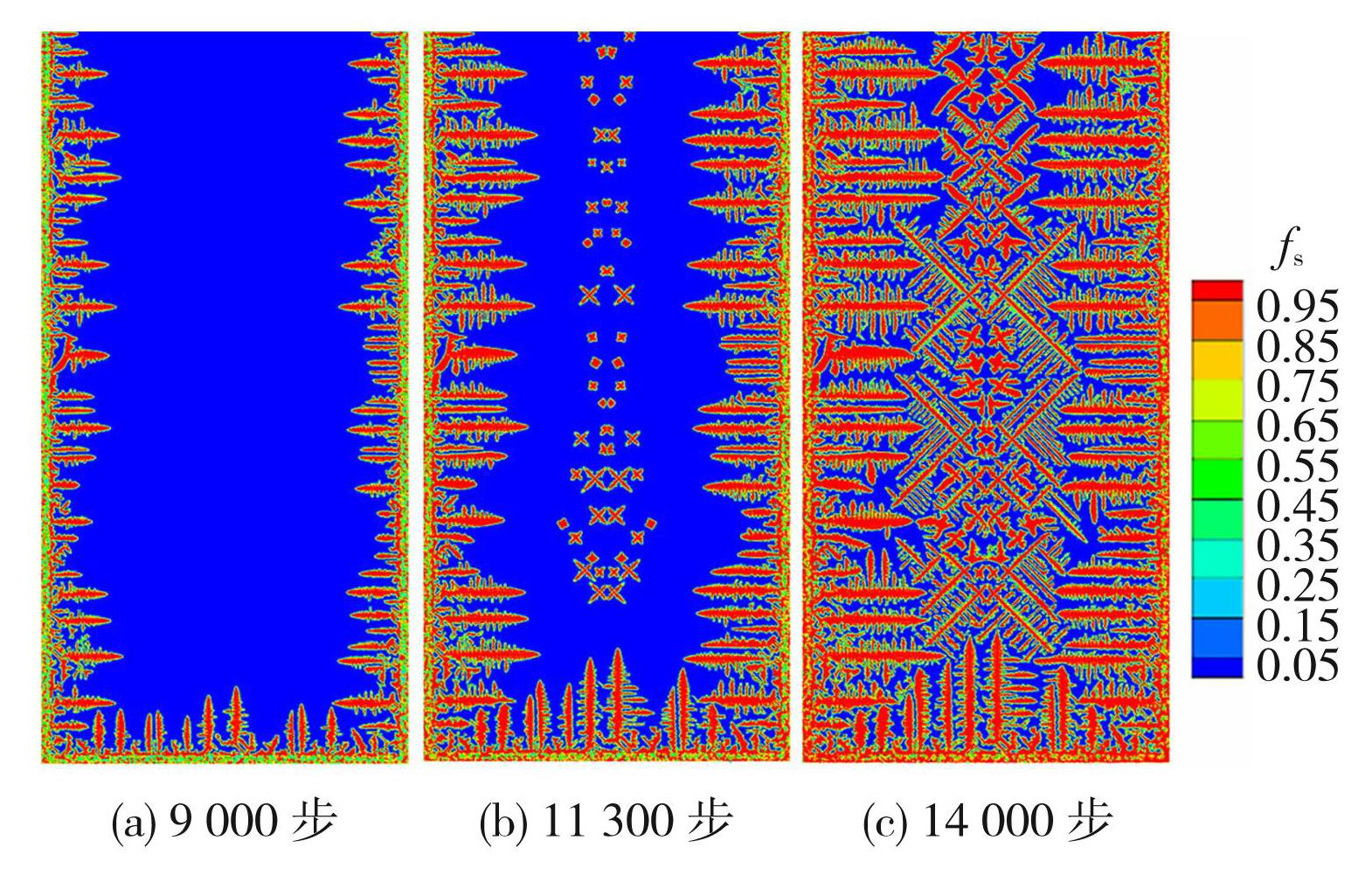
图11CET凝固形貌图

Fig.11Morphology diagram of CET solidification: (a) 9 000 step; (b) 11 300 step; (c) 14 000 step

图12CET凝固溶质分布图

Fig.12Distribution of solute in CET solidification: (a) 9 000 step; (b) 11 300 step; (c) 14 000 step

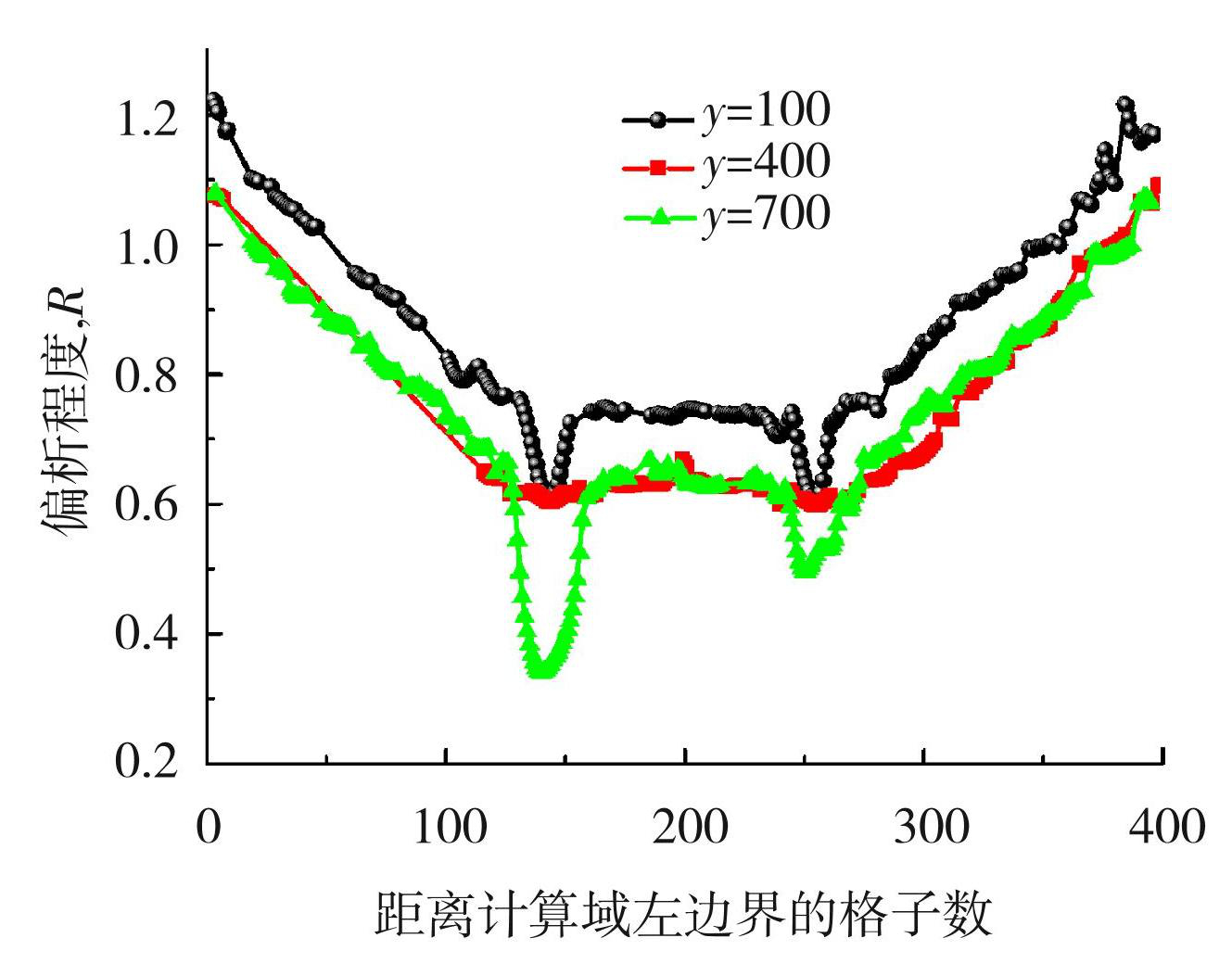
图13CET凝固不同水平高度的偏析程度分布

Fig.13Distribution of segregation degree in CET solidification at different levels

当凝固到11 300步时，计算域开始出现中心等轴晶，等轴晶的择优生长方向各不相同。凝固到14 000步时，中心等轴晶长大。中心等轴晶的出现会导致枝晶间通道变窄，使枝晶前沿溶质扩散变得困难，同时也会阻碍流场流动，使溶质由计算域上方流向下方变得困难。对比图9和图13可以发现，全域柱状晶凝固逆偏析度最大处大于1.4，而以柱状晶向等轴晶转变的形式凝固时逆偏析程度最大为1.2左右，且计算域顶部和底部的偏析程度差要小于全域柱状晶凝固时的偏析程度差。这是因为中心等轴晶的生长过程中也会向其前沿释放溶质，使计算域中间部分溶质浓度增加，等轴晶生长过程中会释放溶质，使溶质浓度升高，此时等轴晶区与柱状晶区前沿（即柱状晶向等轴晶转变部分）溶质浓度相差不大，但是，相对于全域柱状晶凝固的情况，CET凝固时计算域的偏析程度要小一些。

3.4 全域等轴晶凝固的逆偏析分析

图14为计算域全域等轴晶凝固时的形貌图，图15为带有流场的的溶质分布图，图中计算步数分别为8 000、9 100和10 500步。

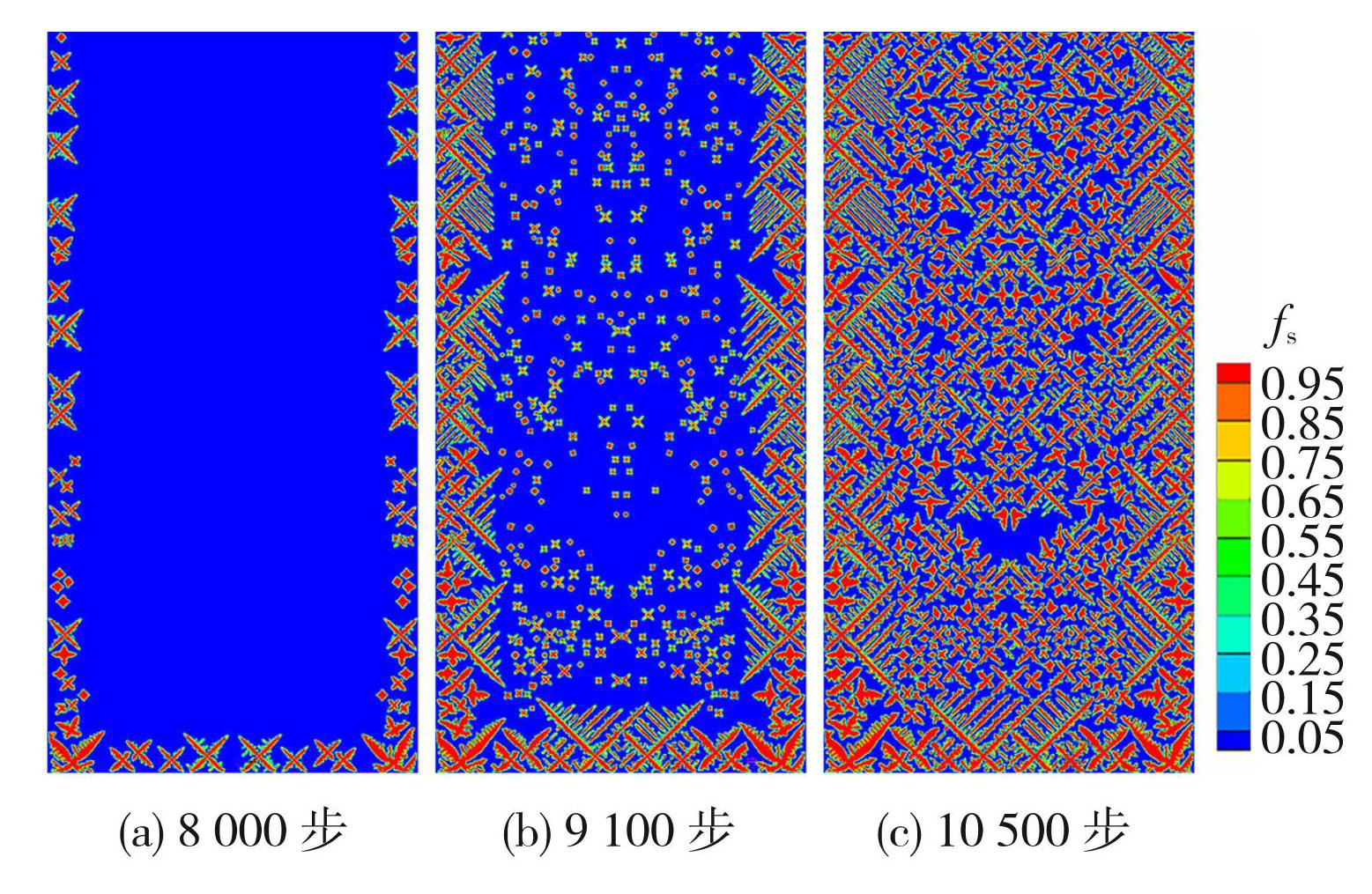
图14全域等轴晶凝固形貌图

Fig.14Morphology diagram of global equiaxed crystal solidification: (a) 8 000 step; (b) 9 100 step; (c) 10 500 step

图15全域等轴晶凝固溶质分布图

Fig.15Distribution of solute in global equiaxed crystal solidification: (a) 8 000 step; (b) 9 100 step; (c) 10 500 step

图16为全域等轴晶凝固时，计算域不同高度的水平偏析度分布图。可见，当计算域凝固到8 000步时，壁面开始出现等轴晶，各等轴晶在其择优角下竞争生长；9 100步时，计算域中心区域的过冷度也达到了等轴晶形核过冷度，出现新的等轴晶生长，同时边界的等轴晶继续生长；10 500步时，等轴晶继续长大，阻碍了流场的流动。

从图15的溶质分布图可以看出全域等轴晶凝固也是会出现逆偏析，特别是在计算域底部左右两侧的角部逆偏析很明显，但是总体来看，逆偏析的程度要远远低于前两种情况。这是因为在全域等轴晶的情况下，当壁面附近区域首先形成等轴晶时，由于等轴晶4个一次枝晶方向（2D）臂长较短，且每个等轴晶的主生长方向各异，不能像柱状晶那样具有方向性的生长优势，排出的溶质浓度高于初始溶质浓度C₀的熔体，相较于前两种情况凝固时，更容易通过自然对流和扩散与中心区域的熔体混合，因而会显著降低偏析程度，即在全域等轴晶的情况下，由于熔体在凝固进程中能够较为充分地混合，所以逆偏析程度大为降低。如图16所示，与前两种凝固形式一样，由于重力作用，溶质也会在计算域底部积聚，导致底部偏析程度要大一些。

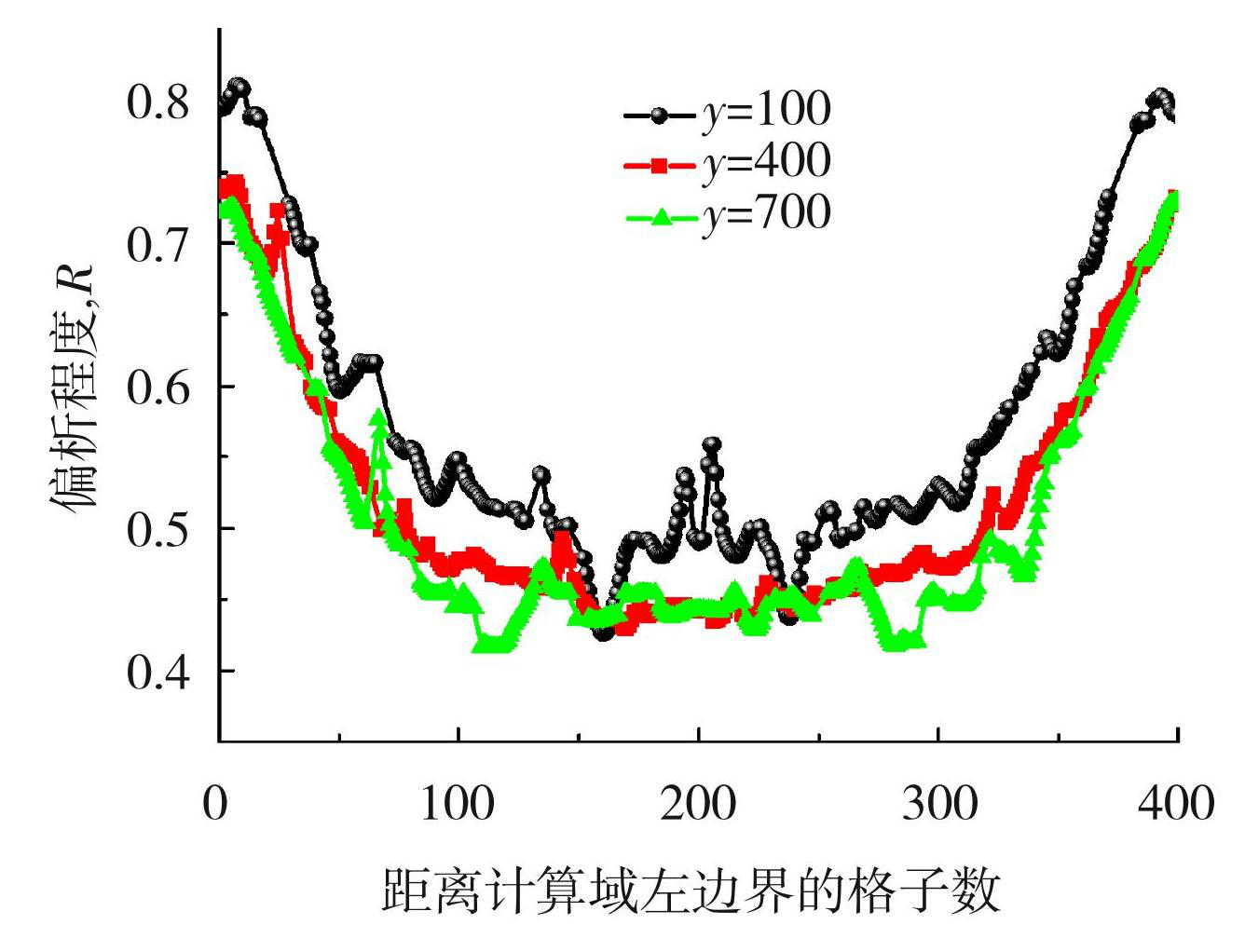
图16全域等轴晶凝固不同水平高度的偏析程度对比

Fig.16Comparison of segregation degree at different levels of global equiaxed crystal solidification

4 讨论

在3种不同的凝固方式中，都出现了逆偏析的现象，如图10、图13、图16所示。凝固组织全为柱状晶时，其偏析度最高达到了1.4左右；凝固组织为柱状晶和等轴晶时，偏析度最高为1.2；以全域等轴晶形式凝固时，其偏析度最高处仅为0.8。随着柱状晶区域的减少，逆偏析程度也逐渐降低，说明柱状晶对枝晶前沿溶质扩散的阻碍作用大于等轴晶。因此在工业生产中要减少逆偏析的影响，可以考虑添加细化剂和孕育剂，尽可能多地获得细化的等轴晶，等轴晶越细小，逆偏析也越小。

由于Cu的密度比Al大，在自然对流的作用下，溶质流向计算域底部，导致计算域底部比上部逆偏析程度更加严重，图10、图13和图16都表现出了这样的情况。在凝固过程中可以通过机械振动或者电磁搅拌，使流场运动无序，使铸锭成分更加均匀。

在不考虑凝固收缩的情况下，仍然出现了逆偏析的现象，分析表明，靠近壁面的冷却速度快导致的凝固温度低，是造成逆偏析的重要原因，而这一点在以往的逆偏析的成因分析中，是未考虑到的。因此要减少逆偏析对铸锭的影响，可以在铸锭凝固过程中适当的降低冷却速率。

5 结论

建立了微观尺度的CA-LBM模型，模拟了凝固组织全为柱状晶、既有柱状晶又有等轴晶以及全为等轴晶3种情况下的组织偏析情况，结果表明均出现了逆偏析的现象。通过对凝固过程的分析研究，得出以下结论。

1）传统的理论认为凝固收缩是形成逆偏析的重要原因，但是本文的研究发现，即使不考虑凝固收缩，也会形成逆偏析。这是发达的二次枝晶对溶质含量较高的熔体流动的分割阻碍，以及壁面处较快的冷却速度和较低的温度所造成的。这是对传统的逆偏析形成机制的重要补充。

2）柱状晶对含有溶质的熔体的分割阻碍作用大于等轴晶。凝固组织全部为柱状晶时，逆偏析最为严重，凝固组织为柱状晶和等轴晶时的逆偏析次之，凝固组织全部为等轴晶的逆偏析最轻。

3）计算域中心区域的熔体在重力作用下沿枝晶间隙流向底部，使得计算域底部的偏析程度大于其他部分。计算域边界冷却速度越快，逆偏析程度就越大。

图1捕获方式

Fig.1Capture rule: (a) Von-Neumann; (b) Moore

下载: 全尺寸图片

图2定向凝固溶质分布图

Fig.2Distribution of solute in directional solidification: (a) 5 000 step； (b) 18 000 step； (c) 32 000 step

下载: 全尺寸图片

图3计算域左右对称轴处偏析程度分布图

Fig.3The distribution diagram of the degree of segregation at the left and right symmetry axes of the computational domain

下载: 全尺寸图片

图4凝固初始条件示意图

Fig.4Initial conditions of solidification

下载: 全尺寸图片

图5全域柱状晶凝固微观组织

Fig.5Microstructure of global columnar solidification: (a) 10 000 step; (b) 13 000 step; (c) 17 000 step

下载: 全尺寸图片

图6全域柱状晶凝固溶质分布图

Fig.6Distribution of solute in global columnar solidification: (a) 10 000 step; (b) 13 000 step; (c) 17 000 step

下载: 全尺寸图片

图7Zone-1（a），Zone-2（b），Zone-3（c）的放大图

Fig.7Enlarged view of Zone-1 (a) , Zone-2 (b) and Zone-3 (c)

下载: 全尺寸图片

图8Al-Cu相图

Fig.8Aluminum-copper phase diagram

下载: 全尺寸图片

图9在不同冷却速率下凝固的偏析程度对比图

Fig.9Comparison diagram of segregation degree of solidification at different cooling rates

下载: 全尺寸图片

图10全域柱状晶凝固不同水平高度的水平偏析度分布

Fig.10Distribution of horizontal segregation at different levels of global columnar solidification

下载: 全尺寸图片

图11CET凝固形貌图

Fig.11Morphology diagram of CET solidification: (a) 9 000 step; (b) 11 300 step; (c) 14 000 step

下载: 全尺寸图片

图12CET凝固溶质分布图

Fig.12Distribution of solute in CET solidification: (a) 9 000 step; (b) 11 300 step; (c) 14 000 step

下载: 全尺寸图片

图13CET凝固不同水平高度的偏析程度分布

Fig.13Distribution of segregation degree in CET solidification at different levels

下载: 全尺寸图片

图14全域等轴晶凝固形貌图

Fig.14Morphology diagram of global equiaxed crystal solidification: (a) 8 000 step; (b) 9 100 step; (c) 10 500 step

下载: 全尺寸图片

图15全域等轴晶凝固溶质分布图

Fig.15Distribution of solute in global equiaxed crystal solidification: (a) 8 000 step; (b) 9 100 step; (c) 10 500 step

下载: 全尺寸图片

图16全域等轴晶凝固不同水平高度的偏析程度对比

Fig.16Comparison of segregation degree at different levels of global equiaxed crystal solidification

下载: 全尺寸图片

表1Al-4.7wt.%Cu合金的热物性参数

Table1Physical properties of Al-4.7wt.%Cu alloy

下载: 全尺寸图片

图1捕获方式

Fig.1Capture rule: (a) Von-Neumann; (b) Moore

图2定向凝固溶质分布图

Fig.2Distribution of solute in directional solidification: (a) 5 000 step； (b) 18 000 step； (c) 32 000 step

图3计算域左右对称轴处偏析程度分布图

Fig.3The distribution diagram of the degree of segregation at the left and right symmetry axes of the computational domain

图4凝固初始条件示意图

Fig.4Initial conditions of solidification

图5全域柱状晶凝固微观组织

Fig.5Microstructure of global columnar solidification: (a) 10 000 step; (b) 13 000 step; (c) 17 000 step

图6全域柱状晶凝固溶质分布图

Fig.6Distribution of solute in global columnar solidification: (a) 10 000 step; (b) 13 000 step; (c) 17 000 step

图7Zone-1（a），Zone-2（b），Zone-3（c）的放大图

Fig.7Enlarged view of Zone-1 (a) , Zone-2 (b) and Zone-3 (c)

图8Al-Cu相图

Fig.8Aluminum-copper phase diagram

图9在不同冷却速率下凝固的偏析程度对比图

Fig.9Comparison diagram of segregation degree of solidification at different cooling rates

图10全域柱状晶凝固不同水平高度的水平偏析度分布

Fig.10Distribution of horizontal segregation at different levels of global columnar solidification

图11CET凝固形貌图

Fig.11Morphology diagram of CET solidification: (a) 9 000 step; (b) 11 300 step; (c) 14 000 step

图12CET凝固溶质分布图

Fig.12Distribution of solute in CET solidification: (a) 9 000 step; (b) 11 300 step; (c) 14 000 step

图13CET凝固不同水平高度的偏析程度分布

Fig.13Distribution of segregation degree in CET solidification at different levels

图14全域等轴晶凝固形貌图

Fig.14Morphology diagram of global equiaxed crystal solidification: (a) 8 000 step; (b) 9 100 step; (c) 10 500 step

图15全域等轴晶凝固溶质分布图

Fig.15Distribution of solute in global equiaxed crystal solidification: (a) 8 000 step; (b) 9 100 step; (c) 10 500 step

图16全域等轴晶凝固不同水平高度的偏析程度对比

Fig.16Comparison of segregation degree at different levels of global equiaxed crystal solidification

表1Al-4.7wt.%Cu合金的热物性参数

Table1Physical properties of Al-4.7wt.%Cu alloy

图(16) / 表(1)

引用本文

张宇,朱宝丰,张士杰,等.基于微观形貌的逆偏析形成机理的数值模拟分析[J].材料科学与工艺，2025，33（1）：31-40.DOI:10.11951/j.issn.1005-0299.20230075

复制

ZHANG Yu，ZHU Baofeng，ZHANG Shijie，et al. Numerical simulation study on the formation mechanism of reverse segregation based on microscopic morphology[J].Materials Science and Technology,2025，33（1）：31-40.DOI:10.11951/j.issn.1005-0299.20230075

Copy

计量

图1捕获方式

Fig.1Capture rule: (a) Von-Neumann; (b) Moore

图2定向凝固溶质分布图

Fig.2Distribution of solute in directional solidification: (a) 5 000 step； (b) 18 000 step； (c) 32 000 step

图3计算域左右对称轴处偏析程度分布图

Fig.3The distribution diagram of the degree of segregation at the left and right symmetry axes of the computational domain

图4凝固初始条件示意图

Fig.4Initial conditions of solidification

图5全域柱状晶凝固微观组织

Fig.5Microstructure of global columnar solidification: (a) 10 000 step; (b) 13 000 step; (c) 17 000 step

图6全域柱状晶凝固溶质分布图

Fig.6Distribution of solute in global columnar solidification: (a) 10 000 step; (b) 13 000 step; (c) 17 000 step

图7Zone-1（a），Zone-2（b），Zone-3（c）的放大图

Fig.7Enlarged view of Zone-1 (a) , Zone-2 (b) and Zone-3 (c)

图8Al-Cu相图

Fig.8Aluminum-copper phase diagram

图9在不同冷却速率下凝固的偏析程度对比图

Fig.9Comparison diagram of segregation degree of solidification at different cooling rates

图10全域柱状晶凝固不同水平高度的水平偏析度分布

Fig.10Distribution of horizontal segregation at different levels of global columnar solidification

图11CET凝固形貌图

Fig.11Morphology diagram of CET solidification: (a) 9 000 step; (b) 11 300 step; (c) 14 000 step

图12CET凝固溶质分布图

Fig.12Distribution of solute in CET solidification: (a) 9 000 step; (b) 11 300 step; (c) 14 000 step

图13CET凝固不同水平高度的偏析程度分布

Fig.13Distribution of segregation degree in CET solidification at different levels

图14全域等轴晶凝固形貌图

Fig.14Morphology diagram of global equiaxed crystal solidification: (a) 8 000 step; (b) 9 100 step; (c) 10 500 step

图15全域等轴晶凝固溶质分布图

Fig.15Distribution of solute in global equiaxed crystal solidification: (a) 8 000 step; (b) 9 100 step; (c) 10 500 step

图16全域等轴晶凝固不同水平高度的偏析程度对比

Fig.16Comparison of segregation degree at different levels of global equiaxed crystal solidification

表1Al-4.7wt.%Cu合金的热物性参数

Table1Physical properties of Al-4.7wt.%Cu alloy

余辉辉, 刘昆, 曾延琦, 等. 电磁搅拌对高锡青铜C5240反偏析和组织的影响[J]. 热加工工艺,2021,50(19):15-7,22.YU Huihui, LIU Kun, ZENG Yanqi,et al. Influence of electromagnetic stirring on inverse segregation and microstructure of C5240 high tin bronze[J]. Hot Working Technology,2021,50(19):15-7,22. DOI:10.14158/j.cnki.1001-3814.20210089

EL-BEALY M O. Advanced solute conservation equations for dendritic solidification processes part I: Experiments and theory[J]. Steel Research International,2013,84(6):565-583. DOI:10.1002/srin.201200228

DONG Q P, CHEN X M, NAGAUMI H,et al. Formation mechanism of macrosegregation in dissimilar-filler welding of aluminum alloys[J]. Journal of Materials Research and Technology,2022,20:26-34. DOI:10.1016/j.jmrt.2022.07.074

ZHAO H D, ZHANG Z F, LI B,et al. Grain size and macrosegregation control of large-sized AA2219 billets by internal electromagnetic stirring in DC casting[J]. Frontiers in Materials,2022,9:892765. DOI:10.3389/fmats.2022.892765

SANTOS J, ZHU B, ZANELLA C,et al. Fatigue crack initiation on semi-solid Al-7Si-Mg castings[J]. Metals,2022,12(7):1061. DOI:10.3390/met12071061

WANG Y D, ZHANG L F. Study on the positive segregation in columnar-to-equiaxed transition zone[J]. Metallurgical Research & Technology,2023,120(1):104. DOI:10.1051/metal/2022108

VYNNYCKY M. On the local solute redistribution equation of macrosegregation,remelting and the formation of channel segregates[J]. International Journal Of Heat And Mass Transfer,2022,190:122737. DOI:10.1016/j.ijheatmasstransfer.2022.122737

CHEN K X, SHEN H F. Numerical simulation of macrosegregation caused by thermal-solutal convection and solidification shrinkage using ALE model[J]. Acta Metallurgica Sinica(English Letters),2019,32(11):1396-1406. DOI:10.1007/s40195-019-00897-0

YU W, LI Y, JIANG T,et al. Solute inverse segregation behavior in twin roll casting of an Al-Cu alloy[J]. Scripta Mater,2022,213:114592. DOI:10.1016/j.scriptamat.2022.114592

SABATINI B J, CZIEGLER A, MODLINGER M. Casting simulations of arsenical copper: New insights into prehistoric metal production and materials[J]. Jom-Us,2020,72(9):3269-3278. DOI:10.1007/s11837-020-04210-8

HUANG S H, LI G Q, ZHANG Z,et al. Effect of cooling rate on the grain morphology and element segregation behavior of Fe-Mn-Al-C low-density steel during solidification[J]. Processes,2022,10(6):1101. DOI:10.3390/pr10061101

PENG P, ZHANG A Q, YUE J M,et al. Macrosegregation and thermosolutal convection-induced freckle formation in dendritic mushy zone of directionally solidified Sn-Ni peritectic alloy[J]. Journal of Materials Science & Technology,2021,75:21-26. DOI:10.1016/j.jmst.2020.08.067

ZHANG Z, BAO Y C, LIU L,et al. Study of the formation mechanism of a-segregation based on microstructural morphology[J]. Metallurgical and Materials Transactions A,2018,49(7):2750-2765. DOI:10.1007/s11661-018-4609-0

ELAHI S M, TAVAKOLI R, ROMERO I,et al. Grain growth competition during melt pool solidification—comparing phase-field and cellular automaton models[J]. Computational Materials Science,2023,216:111882. DOI:10.1016/j.commatsci.2022.111882

ZHANG Y, ZHOU W, TANG J,et al. Understanding effects of ultrasonic vibration on microstructure evolution in hot forming process via cellular automata method[J]. Materials(Basel),2022,15(20):7359. DOI:10.3390/ma15207359

CHEN D L, CHEN W, LIU Y F,et al. A two-relaxation-time lattice boltzmann model for electron beam selective melting additive manufacturing[J]. Frontiers in Materials,2022,9:885481. DOI:10.3389/fmats.2022.885481

ŁACH Ł, SVYETLICHNYY D. New platforms based on frontal cellular automata and lattice boltzmann method for modeling the forming and additive manufacturing[J]. Materials,2022,15(21):7844. DOI:10.3390/ma15217844

HE Y, LIU S. Simulation of the nucleation and crystal growth process in the laser-induced deposition in solution by a lattice boltzmann method[J]. Nanomaterials,2022,12(18):3213. DOI:10.3390/nano12183213

RAPPAZ M, GANDIN C A. Probabilistic modelling of microstructure formation in solidification processes[J]. Acta Metallurgica et Materialia,1993,41(2):345-60. DOI:10.1016/0956-7151(93)90065-Z

ZHU M, STEFANESCU D. Virtual front tracking model for the quantitative modeling of dendritic growth in solidification of alloys[J]. Acta Materialia,2007,55(5):1741-1755. DOI:10.1016/j.actamat.2006.10.037

ZHANG Q Y, SUN D K, PAN S Y,et al. Microporosity formation and dendrite growth during solidification of aluminum alloys: Modeling and experiment[J]. International Journal of Heat And Mass Transfer,2020,146:118838. DOI:10.1016/j.ijheatmasstransfer.2019.118838

FANG H, TANG Q, ZHANG Q,et al. Modeling of microstructure and microsegregation formation during solidification of Al-Si-Mg alloys[J]. International Journal of Heat and Mass Transfer,2019,133:371-381. DOI:10.1016/j.ijheatmasstransfer.2018.12.124

GUO Z, ZHENG C, SHI B. Discrete lattice effects on the forcing term in the lattice Boltzmann method[J]. Physical Review E,2002,65(4):046308. DOI:10.1103/PhysRevE.65.046308

YANG C, XU Q Y, LIU B C. Phase-field-lattice Boltzmann simulation of dendrite growth under natural convection in multicomponent superalloy solidification[J]. Rare Metals,2020,39(2):147-155. DOI:10.1007/s12598-019-01292-5

LIU L, PIAN S, ZHANG Z,et al. A cellular automaton-lattice Boltzmann method for modeling growth and settlement of the dendrites for Al-4.7%Cu solidification[J]. Computational Materials Science,2018,146:9-17. DOI:10.1016/j.commatsci.2018.01.015

WU M, FJELD A, LUDWIG A. Modelling mixed columnar-equiaxed solidification with melt convection and grain sedimentation-Part I: Model description[J]. Computational Materials Science,2010,50(1):32-42. DOI:10.1016/j.commatsci.2010.07.005

WU M, LUDWIG A, FJELD A. Modelling mixed columnar-equiaxed solidification with melt convection and grain sedimentation-Part II: Illustrative modelling results and parameter studies[J]. Computational Materials Science,2010,50(1):43-58. DOI:10.1016/j.commatsci.2010.07.006

高志明, 介万奇, 刘永勤, 等. 微观孔洞和逆偏析缺陷的形成机理与耦合预测研究进展[J]. 金属学报,2018,54(5):717-726.GAO Zhiming, JIE Wanqi, LIU Yongqin,et al. Formation mechanism and coupling prediction of microporosity and inverse segregation: A review[J]. Acta Metallurgica Sinica,2018,54(5):717-726. DOI:10.11900/0412.1961.2017.00501

甘耀强, 张大童, 张卫文, 等. 基于田口方法的挤压铸造Al5Cu0.4Mn合金宏观偏析[J]. 中国有色金属学报,2012,22(12):3386-3394.GAN Yaoqiang, ZHANG Datong, ZHANG Weiwen,et al. Macrosegregation in squeeze-cast Al5Cu0.4Mn alloy based on Taguchi method[J]. The Chinese Journal of Nonferrous Metals,2012,22(12):3386-3394. DOI:10.19476/j.ysxb.1004.0609.2012.12.014

1 计算模型

2 模型验证

3 逆偏析的计算结果讨论

4 讨论

5 结论

友情链接LINKS