运载火箭载荷计算用于获取全箭在气动力、发动机操纵力、晃动力、跨音速脉动压力和阵风作用下的箭体各部段的截面载荷,是结构系统的设计依据。随着运载火箭智能化水平的逐步提高,要求火箭系统在部分故障状态下依然能完成飞行任务[1-8],需要具备一定的故障诊断和处置能力,因此对火箭飞行状态进行载荷监测,这对于箭体结构的安全性评估以及故障的诊断和处置具有重要意义。根据实时载荷计算需求,载荷计算时间需要缩减至毫秒级,同时,根据监测需求,不同于结构设计阶段需要计算箭体全部截面的载荷,只需计算危险或者选定截面载荷即可。目前载荷计算有解析法和有限元法两种方法。解析法采用达朗贝尔原理进行分析[9-14],计算方法为递推计算,即第n个截面载荷计算需要第n-1个截面载荷值,严重影响计算效率,同时,气动力和站点质量加载至载荷站点,若通过减少站点数目方式缩减截面数量,将大幅降低计算精度,因而在不缩减站点数量的基础上计算若干选定截面载荷,需要重新推导载荷计算公式;有限元法是一种通用的计算方法,由于其算法特性导致计算规模往往较大,因而完成解算需要大量的内存空间和计算时间,难以满足飞行载荷打靶仿真和箭上飞行实时计算需求。
本文采用理论公式与代理模型相结合的方式,提出一种载荷的轻量化计算方法,在保证计算精度的同时提高计算效率。首先按照计算量大小对受力分析流程进行了重新规划,并对箭体截面进行分类。然后对于气动、操纵载荷,基于达朗贝尔原理,推导了载荷计算公式,通过预先计算构型相关常值参数降低计算量。最后对于晃动载荷,利用打靶仿真数据构建了多项式代理模型,通过代理模型对晃动载荷进行预测,以进一步降低计算量。
1 载荷计算算法 1.1 受力分析流程由于横向力分析时需要用到轴向力分析结果,首先进行轴向力分析,选取全箭为分析对象,获取全箭轴向加速度ax,以助推为分离体,获取主捆绑位置轴向力Tz,然后进行横向力分析。
在横向力分析中,对于某一计算截面n,截取分离体进行计算,截面载荷轴力T、弯矩M、剪力Q与外力平衡,截面所处位置不同,分离体上所受外力种类不同。根据计算量和流程不同,将全箭截面分为3类(见图 1):第1类为芯级截面,位于理论尖点至前捆绑点之间;第2类为助推截面,位于前、后捆绑点之间;第3类为芯级截面,位于前、后捆绑点之间。

|
图 1 截面分类 Fig. 1 Section classification |
对于第1类截面,首先整体分析获取全箭转动和平动加速度,然后截取分离体,根据气动力、惯性力和截面载荷平衡,获取截面载荷,计算量最小;对于第2类截面,整体分析后,需要取助推为分离体进行计算,获取前捆绑处支反力,然后截取分离体,受力平衡得到截面载荷;对于第3类截面,在整体分析和所有助推前捆绑处支反力计算完成后,才能截取分离体得到截面载荷,具体流程见图 2。

|
图 2 横向力分析计算流程 Fig. 2 Calculation flow of lateral force analysis |
首先进行轴向力分析,获取全箭轴向加速度ax和主捆绑位置轴向力Tz,这一过程比较简单,不详细叙述。
全箭(图 3)在气动力、操纵力、惯性力下受力平衡,以偏航方向为例,考虑故障工况,可以得到全箭转动加速度和平动加速度分别为:
| $ \begin{aligned} a_z= & \left\{F_{\mathrm{q}}\left(C_{\mathrm{P}}-C_{\mathrm{M}}\right)-F_{\mathrm{c}}\left(x_{\mathrm{fk}}-C_{\mathrm{M}}\right)+\right. \\ & {\left.\left[\left(T_{\mathrm{ZX} 2}-a_x m_{\mathrm{Z} 2}\right)-\left(T_{\mathrm{ZX} 4}-a_{\mathrm{x}} m_{\mathrm{Z4}}\right)\right] l_{\mathrm{XZ}}\right\} / J } \end{aligned} $ | (1) |
| $ a_{\mathrm{p}}=\left(F_{\mathrm{q}}+F_{\mathrm{c}}\right) / m $ | (2) |

|
图 3 全箭受力分析 Fig. 3 Force analysis of launch vehicle |
式中:Fq为全箭气动力合力,Fc为全箭操纵力合力,CP为全箭压心位置到理论尖点距离,CM为全箭质心位置到理论尖点距离,xfk为操纵力作用位置到理论尖点距离,TZX2为Ⅱ象限助推总推力,TZX4为Ⅳ象限助推总推力,mZ2为Ⅱ象限助推总质量,mZ4为Ⅳ象限助推总质量,lXZ为芯级轴线到助推轴线的距离,J为全箭转动惯量,m为全箭总质量,ax为全箭轴向加速度,az为全箭转动角加速度,ap为全箭横向平动加速度。
由于推进剂质量随飞行时间逐渐减小,而结构质量为常值(同一飞行阶段),在计算时将在飞行中不发生变化的质量和发生变化的推进剂质量分开,对于助推飞行段,有
| $ \left\{\begin{aligned} M= & \sum\limits_{i=1}^N m_i+m_{\mathrm{r1}}+m_{\mathrm{y} 1}+\sum\limits_{k=1}^{n_{\mathrm{zt}}} m_{\mathrm{zky}}+\sum\limits_{k=1}^{n_{\mathrm{zt}}} m_{\mathrm{zkr}} \\ J= & \sum\limits_{i=1}^N m_i\left(l_i-C_{\mathrm{M}}\right)^2+m_{\mathrm{r1}}\left(l_{\mathrm{r} 1}-C_{\mathrm{M}}\right)^2+m_{\mathrm{y} 1}\left(l_{\mathrm{y} 1}-C_{\mathrm{M}}\right)^2+ \\ & \sum\limits_{k=1}^{n_{\mathrm{zt}}} m_{\mathrm{zky}}\left(l_{\mathrm{zky}}-C_{\mathrm{M}}\right)^2+\sum\limits_{k=1}^{n_{\mathrm{zt}}} m_{\mathrm{zkr}}\left(l_{\mathrm{zkr}}-C_{\mathrm{M}}\right)^2 \end{aligned}\right. $ | (3) |
式中:N为全箭站点个数,mi为站点结构质量和二、三级贮箱推进剂质量分站之和(在飞行过程中常值);nzt为助推器个数, li为第i个质量分站到理论尖点距离,ly1为一级氧箱推进剂质心位置到理论尖点距离,lr1为一级燃箱推进剂质心位置到理论尖点距离,lzky为助推氧箱推进剂质心位置到理论尖点距离,lzkr为助推燃箱推进剂质心位置到理论尖点距离。
转动惯量J中:
| $ \sum\limits_{i=1}^N m_i\left(l_i-C_{\mathrm{M}}\right)^2=C_{\mathrm{M}}^2 \sum\limits_{i=1}^N m_i-2 C_{\mathrm{M}} \sum\limits_{i=1}^N m_i l_i+\sum\limits_{i=1}^N m_i l_i^2 $ | (4) |
式中:
| $ \left\{\begin{array}{l} M= & M_{\mathrm{cz}}+m_{\mathrm{r} 1}+m_{\mathrm{y} 1}+\sum\limits_{k=1}^{n_{\mathrm{zt}}} m_{\mathrm{zky}}+\sum\limits_{k=1}^{n_{\mathrm{zt}}} m_{\mathrm{zkr}}\\ J= & C_{\mathrm{M}}^2 M_{\mathrm{cz}}-2 C_{\mathrm{M}} M_{\mathrm{cz} \_1 \mathrm{m}}+M_{\mathrm{cz} \_\mathrm{2m}}+m_{\mathrm{r} 1}\left(l_{\mathrm{r} 1}-C_{\mathrm{M}}\right)^2+\\ & m_{\mathrm{y} 1}\left(l_{y 1}-C_{\mathrm{M}}\right)^2+\sum\limits_{k=1}^{n_{\mathrm{zt}}} m_{\mathrm{zky}}\left(l_{\mathrm{zky}}-C_{\mathrm{M}}\right)^2+\\ & \sum\limits_{k=1}^{n_{\mathrm{zt}}} m_{\mathrm{zkr}}\left(l_{\mathrm{zkr}}-C_{\mathrm{M}}\right)^2 \end{array}\right. $ | (5) |
式中ly1、lr1为推进剂质心位置可以通过推进剂质量进行插值,两者基本为线性关系,为减小计算量,对推进剂质心随质量变化曲线用多项式进行拟合。
这样,可以通过提前计算Mcz、Mcz_1m、Mcz_2m以及多项式拟合系数,减小计算量。
1.2.2 助推受力分析选取助推为分析对象,在气动力Fq_zt、惯性力Fg_zt、操纵力Fc_zt以及捆绑支反力下受力平衡,由于惯性力已知,可以求得捆绑支反力R1和R2(见图 4)。

|
图 4 助推受力分析 Fig. 4 Force analysis of booster |
惯性力和对前捆绑点力矩分别为:
| $ F_{\mathrm{g}\_\mathrm{zt}}=-\left(\sum\limits_{i=1}^{N_{\mathrm{zt}}} m_i a_z\left(C_{\mathrm{M}}-l_i\right)+\sum\limits_{i=1}^{N_{\mathrm{zt}}} m_i a_{\mathrm{p}}\right) $ | (6) |
| $ M_{\mathrm{g\_zt}}=-\left(\sum\limits_{i=1}^{N_{\mathrm{zt}}} m_i a_z\left(C_{\mathrm{M}}-l_i\right)\left(l_i-x_{\mathrm{BZ1}}\right)+\sum\limits_{i=1}^{N_{\mathrm{zt}}} m_i a_{\mathrm{p}}\left(l_i-x_{\mathrm{BZ1}}\right)\right) $ | (7) |
令
| $ F_{\mathrm{g} \_\mathrm{zt}}=M_{\mathrm{cz} \_\mathrm{zt} \_\mathrm{1m}} \cdot a_z-M_{\mathrm{cz} \_\mathrm{zt}} \cdot\left(C_{\mathrm{M}} a_z+a_{\mathrm{p}}\right) $ | (8) |
| $ \begin{array}{l} M_{{\mathrm{g} \_\mathrm{zt}}}= & M_{\mathrm{cz} \_\mathrm{zt} \_\mathrm{2m}} \cdot a_z- M_{\mathrm{cz} \_\mathrm{zt} \_\mathrm{1m}} \cdot\left[\left(C_{\mathrm{M}}+x_{\mathrm{BZ1}}\right) a_z+a_{\mathrm{p}}\right]+\\ & M_{\mathrm{cz} \_\mathrm{zt}} \cdot\left(x_{\mathrm{BZ} 1} C_{\mathrm{M}} a_z+x_{\mathrm{BZ} 1} a_{\mathrm{p}}\right) \end{array} $ | (9) |
根据平衡方程:
| $ F_{\mathrm{g} \_\mathrm{zt}}=R_{1 \mathrm{~g}}+R_{2 \mathrm{~g}} $ | (10) |
| $ M_{\mathrm{g}\_ \mathrm{zt}}=R_{2 \mathrm{~g}}\left(x_{\mathrm{BZ2}}-x_{\mathrm{BZ1}}\right) $ | (11) |
可以求得惯性力引起的前捆绑支反力R1g,同理可以求得操纵力、气动力、主捆绑轴向力引起的支反力,相加得到前捆绑总支反力R1,详细过程不再赘述。和全箭受力分析相同,可以提前计算常值参数以减小计算量。
1.2.3 截面载荷 1.2.3.1 第1类截面对于第1类截面,截取分离体进行分析(见图 5),截面站点号为n,在气动力Fqn、惯性力Fgn、截面载荷下平衡。

|
图 5 第1类截面受力分析 Fig. 5 Force analysis of the first type of section |
气动力和气动力矩分别为:
| $ F_{\mathrm{q} n}=\sum\limits_{i=1}^n C_{\mathrm{ipm}} \Delta l_i \cdot q \cdot S_{\mathrm{M}} $ | (12) |
| $ M_{\mathrm{q} n}=\sum\limits_{i=1}^n C_{\mathrm{ipm}} \Delta l_i \cdot q \cdot S_{\mathrm{M}} \cdot\left(l_n-l_i\right) $ | (13) |
式中:Cipm为气动载荷分布,Δli为Cipm作用长度。
惯性力和惯性力矩分别为:
| $ F_{\mathrm{g} n}=\sum\limits_{i=1}^n m_i \cdot\left[\left(C_{\mathrm{M}}-l_i\right) a_z+a_{\mathrm{p}}\right] $ | (14) |
| $ M_{\mathrm{g}n}=\sum\limits_{i=1}^n m_i \cdot\left[\left(C_{\mathrm{M}}-l_i\right) a_z+a_{\mathrm{p}}\right] \cdot\left(l_n-l_i\right) $ | (15) |
定义
| $ F_{\mathrm{q} n}=C_{\mathrm{ncz}} \cdot q \cdot S_{\mathrm{M}} $ | (16) |
| $ M_{\mathrm{q} n}=C_{\mathrm{ncz}} \cdot q \cdot S_{\mathrm{M}} \cdot l_n-C_{\mathrm{ncz} \_1 \mathrm{m}} \cdot q \cdot S_{\mathrm{M}} $ | (17) |
惯性力和惯性力矩分别为:
| $ F_{\mathrm{g} n}=M_{\mathrm{ncz}} \cdot\left(C_{\mathrm{M}} a_z+a_{\mathrm{p}}\right)+M_{\mathrm{ncz} \_1 \mathrm{m}} \cdot a_z $ | (18) |
| $ \begin{aligned} M_{\mathrm{g}n}= & M_{\mathrm{ncz}} \cdot\left(C_{\mathrm{M}} a_z+a_{\mathrm{p}}\right) \cdot l_n-M_{\mathrm{ncz} \_1 \mathrm{m}} \cdot \\ & {\left[\left(l_n+C_{\mathrm{M}}\right) a_z+a_{\mathrm{p}}\right]+M_{\mathrm{ncz}\_ 2 \mathrm{m}} \cdot a_z } \end{aligned} $ | (19) |
然后根据平衡关系可以得到截面载荷分别为:
| $ Q_n=F_{\mathrm{q} n}-F_{\mathrm{g}n} $ | (20) |
| $ M_n=M_{\mathrm{q} n}-M_{\mathrm{g} n} $ | (21) |
对于常值Cncz、Cncz_1m、Mncz、Mncz_1m、Mncz_2m,可以提前计算,减小计算量。由于气动载荷分布包含不同攻角,需要计算不同攻角下的Cncz、Cncz_1m,然后根据实际攻角进行插值。
1.2.3.2 第2类截面对于第2类截面,取分离体,在气动力、惯性力、支反力、截面载荷下受力平衡,见图 6。图 6中气动力和惯性力计算方法与第1类截面相同,根据平衡方程可以得到截面载荷为
| $ \left\{\begin{aligned} Q_n= & F_{\mathrm{q} n}-F_{\mathrm{g} n}-R_1 \\ M_n= & M_{\mathrm{q} n}-M_{\mathrm{g} n}-R_1 \cdot\left(l_n-x_{\mathrm{BZ} 1}\right)+ \\ & T_z \cdot\left(l_{\mathrm{XZ}}-l_{\mathrm{KB}}\right) \end{aligned}\right. $ | (22) |

|
图 6 第2类截面受力分析 Fig. 6 Force analysis of the second type of section |
对于第3类截面,取分离体,在气动力、惯性力、支反力、截面载荷下受力平衡,见图 7。图 7中气动力和惯性力计算方法与第1类截面相同,以偏航方向为例,根据平衡方程可以得到截面载荷为
| $ \left\{\begin{aligned} Q_n= & F_{\mathrm{q} n}-F_{\mathrm{g}n}+R_{1\mathrm{z}2}-R_{1\mathrm{z}4} \\ M_n= & M_{\mathrm{q} n}-M_{\mathrm{g} n}-\left(R_{1\mathrm{z}4}-R_{1\mathrm{z}2}\right) \cdot\left(l_n-x_{\mathrm{BZ} 1}\right)+ \\ & \left(T_{\mathrm{z} 4}-T_{\mathrm{z} 2}\right) \cdot\left(l_{\mathrm{XZ}}-l_{\mathrm{KB}}\right) \end{aligned}\right. $ | (23) |

|
图 7 第3类截面受力分析 Fig. 7 Force analysis of the third type of section |
横向载荷计算中需考虑不同晃动力方向组合,计算次数为2(n-1)次(n为贮箱个数,考虑每个贮箱推进剂晃动力为正、负两种情况),对计算效率影响较大。由于晃动载荷相比气动、操纵等载荷在全箭载荷中占比较小,可以尝试采用系数拟合的方式进行计算。
横向总载荷计算时,将气动载荷、操纵载荷作为主项,将晃动载荷、气动载荷偏差、操纵载荷偏差和弹性载荷的均方和作为偏差项,绝对值相加得到总载荷为
| $ H=H_{\mathrm{q}}+H_{\mathrm{c}}+\sqrt{\Delta H_{\mathrm{q}}^2+\Delta H_{\mathrm{c}}^2+H_{\mathrm{h}}^2+H_{\mathrm{t}}^2} $ | (24) |
式中:H为横向总载荷,包括弯矩与横向力;Hq为气动载荷,Hc为操纵载荷,Ht为弹性载荷,Hh为晃动载荷,ΔHq为气动载荷偏差,ΔHc为操纵载荷偏差。
若不考虑偏差,则总载荷为
| $ H=H_{\mathrm{q}}+H_{\mathrm{c}}+\sqrt{H_{\mathrm{h}}^2+H_{\mathrm{t}}^2} $ | (25) |
无晃动载荷为
| $ \tilde{H}=H_{\mathrm{q}}+H_{\mathrm{c}}+H_{\mathrm{t}} $ | (26) |
对于晃动载荷Hh,晃动力Fh=m1ω12Yk,其中一阶晃动频率[15]为
| $ \omega_1=\sqrt{\frac{n_x g_0 \xi_1}{R} \tanh \left(\frac{\xi_1 h_{\mathrm{e}}}{R}\right)} $ | (27) |
式中:nx为飞行轴向过载,g0为重力加速度,R为贮箱半径,he为等效液位高度,ξ1为第1类贝塞尔函数的一阶根。式中参数除nx外只与贮箱内剩余推进剂质量相关,因此定义对于过载归一化的晃动频率
定义量纲一的晃动拟合系数为
| $ k_{\mathrm{h}}=\frac{H_{\mathrm{n}}-\tilde{H}_{\mathrm{n}}}{\bar{F}_{\mathrm{h}} \cdot n_x \cdot l_{\mathrm{hd}}} $ | (28) |
式中: lhd为等效晃动力臂,即晃动力作用位置到质心的距离。晃动力作用位置与贮箱内推进剂质量相关,可以通过预先计算晃动特性得到。kh可以部分去除飞行过载、晃动力大小对晃动载荷的影响,但晃动方向组合等因素对晃动载荷影响较为复杂,其反映在kh的散差中。
通过打靶仿真计算,可以得到kh与飞行马赫数的关系,采用多项式代理模型对kh进行拟合,因此,可以通过
| $ \hat{H}=\tilde{H}+k_{\mathrm{h}} \cdot \bar{F}_{\mathrm{h}} \cdot n_x \cdot l_{\mathrm{hd}} $ | (29) |
计算流程见图 8。首先选定计算截面,然后计算常值参数,常值参数反映了构型相关参数,包含气动相关、质量相关以及弹性载荷等参数,通过预先计算常值参数,可以避免复杂的累加求和计算,大幅降低计算量。飞行参数可以根据TGNC仿真或者飞行实时获取,然后根据公式计算截面载荷。最后利用晃动代理模型修正载荷,得到最终载荷结果。

|
图 8 计算流程 Fig. 8 Calculation process |
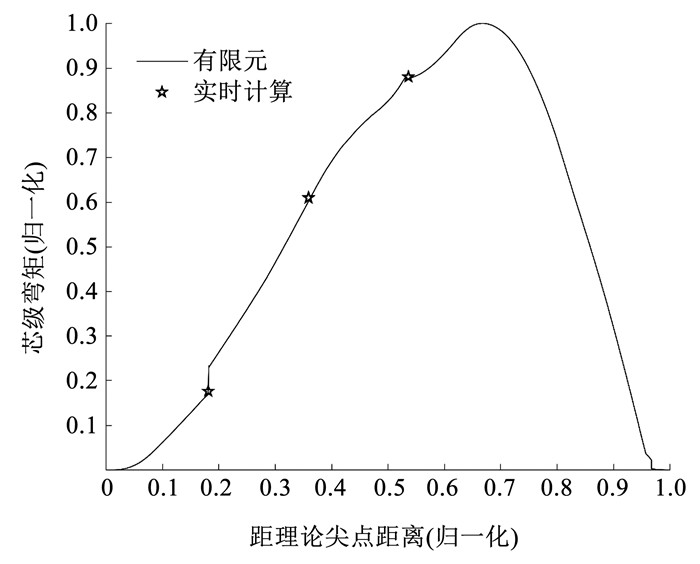
为验证计算公式的正确性,以某型两助推运载火箭跨音速飞行工况为例,建立有限元模型,箭体捆绑连接方式为前捆绑传力,采用梁单元进行建模,如图 9所示,共选取了5个截面进行计算,见表 1。表 1中包含第1类和第2类截面各2个,第3类截面1个,与有限元计算结果进行对比,芯级截面、助推截面对比结果如图 10、11所示,偏差均小于5%,满足工程应用需求。
|
图 9 有限元模型 Fig. 9 Finite element model |
| 表 1 计算截面 Tab. 1 Calculation section |
|
图 10 芯级弯矩 Fig. 10 Bending moment of core |

|
图 11 助推弯矩 Fig. 11 Bending moment of booster |
截面选取的原则主要结合箭体设计的承载能力,选取飞行载荷接近承载能力的危险截面。同时对于一些飞行中可能出现的故障工况,选取影响较大的箭体截面,例如在助推发动机故障情况下,两侧助推轴向力产生差异,箭体主捆绑传力点附近会产生附加弯矩。
4 计算效率采用Windows7系统,运行软件为Matlab2017a,电脑配置CPU为i7-6700,内存大小为16 G,共运行3次,平均计算时间见表 2。运行总平均时间为7.7 ms,达到毫秒级,满足计算速度要求。相同运行环境下,原方法[9]计算时间为秒级,计算效率大幅调高,为评估计算效率提升的效果大小,设气动、操纵、晃动载荷的单个截面计算一次的时间为t0,则可估计原方法总计算时间t_old=(2+2n-1)×N×t0, 本文方法的计算时间为t_new=3×N_new×t0。对于本文中算例,贮箱个数n=8, 截面数量N=120, N_new=5, 可以得到t_old/t_new=1 040倍,与实际情况相当,由于估算公式中没有详细考虑不同类型载荷计算量之间差异以及数据插值等过程,估算计算效率与实际情况有些差异,能粗略反映实际情况。
| 表 2 计算效率 Tab. 2 Computing efficiency |
在实际应用中,考虑到运行环境的差异,可以通过缩减截面的方式适应运行时间要求,进一步提高运行速度。同时,由于不同飞行时间下箭体载荷的变化规律不同,关注截面位置不同,因而可以根据不同飞行时段,切换计算截面,满足计算时间需求。
5 结论1) 在计算效率方面,通过预先计算结构相关常值项,提高气动和操纵载荷计算效率,对于占比较小的晃动载荷,构建多项式代理模型进行预测,进一步提高计算效率。利用某两助推构型火箭进行算例测试,通过合理选择截面数量,单秒态计算时间由秒级大幅提升至毫秒级,达到实时计算水平,满足飞行载荷实际计算需求。
2) 在计算精度方面,由于气动和操纵载荷采用理论公式进行计算,可以保证计算精度,对于占比较小的晃动载荷采用多项式代理模型进行预测,对总载荷计算精度影响较小。研究结果表明,与有限元结果进行对比,箭体不同类型截面计算偏差均小于5%,满足工程应用精度要求。
| [1] |
李爽, 刘旭, 叶松, 等. 运载火箭动力系统故障下制导控制技术研究进展[J]. 上海航天(中英文), 2022, 39(4): 76. LI Shuang, LIU Xu, YE Song, et al. Overview of guidance and control technologies for launch vehicles under propulsion system faults[J]. Aerospace Shanghai(Chinese & English), 2022, 39(4): 76. DOI:10.19328/j.cnki.2096-8655.2022.04.008 |
| [2] |
常武权, 张志国. 运载火箭故障模式及制导自适应技术应用分析[J]. 宇航学报, 2019, 40(3): 302. CHANG Wuquan, ZHANG Zhiguo. Analysis of fault modes and applications of self-adaptive guidance technology for launch vehicle[J]. Journal of Astronautics, 2019, 40(3): 302. DOI:10.3873/j.issn.1000-1328.2019.03.007 |
| [3] |
曲晶, 张绿云. 国外火箭发射及故障情况统计分析[J]. 中国航天, 2016(2): 13. QU Jing, ZHANG Luyun. Statistical analysis of rocket launch and failure in foreign countries[J]. Aerospace China, 2016(2): 13. |
| [4] |
朱海洋, 吴燕生, 陈宇, 等. 适应运载火箭推力下降故障的神经网络容错控制方法[J]. 航天控制, 2019, 37(4): 3. ZHU Haiyang, WU Yansheng, CHEN Yu, et al. A neural network fault-tolerant control method for launch vehicles with thrust decline[J]. Aerospace Control, 2019, 37(4): 3. DOI:10.16804/j.cnki.issn1006-3242.2019.04.001 |
| [5] |
孙成志, 闫晓东. 基于神经网络和证据理论的火箭发动机故障诊断[J]. 宇航总体技术, 2020, 4(4): 20. SUN Chengzhi, YAN Xiaodong. Fault diagnosis of rocket engine based on neural network and evidence theory[J]. Astronautical Systems Engineering Technology, 2020, 4(4): 20. |
| [6] |
HABERKORN T, MARTINON P, GERGAUD J. Low-thrust minimum-fuel orbital transfer: a homotopic approach[J]. Journal of Guidance, Control, and Dynamics, 2004, 27(6): 1046. DOI:10.2514/1.4022 |
| [7] |
LIAO Yuxin, LI Huifeng, BAO Weimin. Indirect Radau pseudospectral method for the receding horizon control problem[J]. Chinese Journal of Aeronautics, 2016, 29(1): 215. DOI:10.1016/j.cja.2015.12.023 |
| [8] |
SONG Zhengyu, WANG Cong, GONG Qinghai. Joint dynamic optimization of the target orbit and flight trajectory of a launch vehicle based on state-triggered indices[J]. Acta Astronautica, 2020, 174: 82. DOI:10.1016/j.actaastro.2020.04.017 |
| [9] |
国防科学技术工业委员会. 地地弹道式导弹和运载火箭载荷设计: QJ 2619—1994[S]. 北京: 中国航天工业总公司, 1994
|
| [10] |
邹经湘, 于开平. 结构动力学[M]. 2版. 哈尔滨: 哈尔滨工业大学出版社, 2009. Zou Jingxiang, YU Kaiping. Dynamics of Structures[M]. 2nd ed. Harbin: Harbin Institute of Technology Press, 2009. |
| [11] |
张静, 戴婷婷, 闫奕含, 等. 固体火箭飞行静载荷计算的偏差使用方法优化[J]. 宇航总体技术, 2022, 6(6): 9. ZHANG Jing, DAI Tingting, YAN Yihan, et al. Using method optimization of deviation for static flight load calculation of solid rocket[J]. Astronautical Systems Engineering Technology, 2022, 6(6): 9. |
| [12] |
袁赫, 李静琳, 宋征宇, 等. 运载火箭飞行载荷联合优化控制技术[J]. 宇航学报, 2022, 43(10): 1291. YUAN He, LI Jinglin, SONG Zhengyu, et al. Joint optimal control technology of launch vehicle flight load[J]. Journal of Astronautics, 2022, 43(10): 1291. DOI:10.3873/j.issn.1000-1328.2022.10.002 |
| [13] |
王锋. 运载火箭载荷计算及通用软件实现[D]. 长沙: 国防科学技术大学, 2001 WANG Feng. Load calculation and general software implementation of launch vehicle[D]. Changsha: National University of Defense Technology, 2001 |
| [14] |
王亮, 张妍, 蔡毅鹏, 等. 基于概率浮动的战术导弹载荷设计方法研究[J]. 强度与环境, 2019, 46(2): 31. WANG Liang, ZHANG Yan, CAI Yipeng, et al. Study on the load design of tactical missile base on the probability exchange[J]. Structure & Environment Engineering, 2019, 46(2): 31. DOI:10.19447/j.cnki.11-1773/v.2019.02.006 |
| [15] |
国防科学技术工业委员会. 地—地导弹、运载火箭液体推进剂晃动设计规范: QJ 2117—1991[S]. 北京: 中国航天工业总公司, 1991
|
 2024, Vol. 56
2024, Vol. 56


