2. 江南大学 物联网技术应用教育部工程研究中心,江苏 无锡 214122
2. Engineering Research Center of Internet of Things Technology Applications Ministry of Education, Jiangnan University, Wuxi 214122, Jiangsu, China
信息物理系统(cyber-physical systems, CPS)由深度集成、紧密耦合的计算和物理组件组成,CPS中的执行器和传感器通过无线通信网络进行数据传输、监控、管理和感知,广泛应用于工业环境中,形成工业信息物理系统(industrial cyber-physical systems, ICPS)。ICPS中的数据反映了系统动态特征的演变[1],但是由于无线通信网络的脆弱性,极易遭受拒绝服务(denial of service, DoS)攻击、虚假数据注入(false data injection, FDI)攻击、重放攻击等网络攻击的入侵[2]。
目前的研究主要针对仅包含单个被控对象ICPS的攻击以及防御策略的研究。文献[3]采用3层攻击模型(模型知识、攻击策略和破坏矩阵)构建DoS攻击、FDI攻击和重放攻击的攻击模型。文献[4]采用弹性预测控制策略,保证系统在DoS攻击下的指数稳定性。文献[5]采用有限时域控制器,确保遭受包含DoS攻击和FDI攻击的闭环系统的性能。文献[6]设计极大极小控制器, 保证系统在攻击和干扰下的鲁棒性。文献[7]设计了事件触发弹性控制策略, 降低攻击对系统的影响。文献[8]基于弹性观测器设计控制器,提高系统在DoS攻击下的弹性。当前ICPS中大多存在多个被控对象,攻击者不断发掘系统漏洞并提升攻击手段, 可以瘫痪控制系统, 造成级联事故[9-11],而由多个被控对象组成的ICPS的研究还比较匮乏,因此对于由多个被控对象组成的ICPS在攻击下的控制问题值得深入研究。
当前对于由多个被控对象组成的系统模型研究中,文献[12]利用多智能体系统的自组织能力和智能协调能力,设计了基于多智能体系统的CPS端。文献[13]将CPS传感网络中的物理节点与多智能体系统的智能体结合,设计智能需求侧管理系统,并将其应用于光伏供电。上述文献[12-13]结合多智能体系统,为多个被控对象组成的系统模型研究提供了思路。
对于多智能体和ICPS的融合系统,保证多智能体在遭受攻击和外界干扰时的一致性具有重大意义。文献[14]设计DoS攻击下基于边缘事件触发机制的多智能体系统一致性控制协议。文献[15]对具有外部干扰和DoS攻击下的多智能体系统设计分布式无模型自适应控制算法。文献[16]研究在DoS攻击和干扰下的多智能体系统的弹性分布式一致性控制问题。文献[17-19]采用鲁棒控制方法,分别实现了在攻击和干扰下的鲁棒输出一致。上述文献[14-19]在攻击和干扰下设计一致性控制协议时,采用系统原始状态信息,未考虑攻击或干扰存在时,系统通信信道被堵塞、信息缺失的情况,因此考虑攻击干扰下系统状态信息变化的情况具有现实意义。另外,对于线性矩阵不等式(linear matrix inequality, LMI)中参数约束、最优设计问题也值得深入研究。
基于上述讨论, 本文旨在研究ICPS在遭受DoS攻击和不确定外界扰动时的最优一致性控制问题。首先,考虑由多个被控对象构成的ICPS,根据多智能体中单个智能体能够感知环境、执行动作影响环境的特点,将ICPS中执行器、传感器、被控对象描述为智能体,构建固定拓扑的多智能体ICPS模型。其次,考虑更具一般性的双通道DoS攻击,采用状态观测器重构攻击时被堵塞的状态信息, 将多智能体中拓扑结构、受攻击后的系统变化,利用Kronecker乘积进行整体建模,给出了包括系统误差、状态变量、受控输出在内的更为完整的系统模型,解决一类DoS攻击建模问题,并解决攻击下未考虑系统通信信道堵塞、信息缺失的问题。最后,针对干扰抑制水平的约束问题,引入零和博弈理论,将系统输入和外部干扰视为博弈中参与者,通过博弈中的优化问题,结合系统的H∞一致性条件,构建基于零和博弈的最优H∞一致性设计框架,达到最优H∞一致性设计,解决LMI中的参数约束问题。
1 模型构建 1.1 多智能体ICPS模型考虑由N个智能体组成的多智能体ICPS,其中第i个智能体εi由第i组执行器、被控对象和传感器组成,见图 1。

|
图 1 多智能体ICPS框图 Fig. 1 Multi-agent ICPS block diagram |
智能体i可建模为
| $ \left\{\begin{array}{l} \boldsymbol{x}_{i, k+1}=\boldsymbol{A} \boldsymbol{x}_{i, k}+\boldsymbol{B}_1 \boldsymbol{u}_{i, k}+\boldsymbol{B}_2 \boldsymbol{\varpi}_{i, k} \\ \boldsymbol{z}_{i, k}=\boldsymbol{C}_1 \boldsymbol{x}_{i, k}+\boldsymbol{D}_1 \boldsymbol{\varpi}_{i, k} \\ \boldsymbol{y}_{i, k}=\boldsymbol{C}_2 \boldsymbol{x}_{i, k}+\boldsymbol{D}_2 \boldsymbol{\varpi}_{i, k} \end{array}\right. $ | (1) |
式中:k=1, 2, …, T为有限时域时刻,xi, k∈ Rn为系统状态变量,ui, k∈Rm为控制变量,zi, k∈Rr为受控输出,yi, k∈Rp为传感器测量输出,ϖi, k∈ Rq为不确定外界干扰。A、B1、B2、C1、C2、D1、D2为已知的实系统参数矩阵。
考虑N个多智能体的通信拓扑结构为无向图G{ ε,
无向图G的Laplacian矩阵为M =[lij]∈ RN×N,矩阵中的元素lij取值为
| $ l_{i j}= \begin{cases}-a_{i j}, & i \neq j \\ \sum\limits_{j=1, j \neq i}^N a_{i j}, & i=j\end{cases} $ | (2) |
注1 对于固定通信拓扑结构为G{ ε,
在DoS攻击下,无线通信网络中传输的数据包丢失,会破坏整个系统的一致性能。
DoS攻击对ICPS无线通信网络发起进攻:1)测量输出在通过无线通信网络传输到控制器时会遭受攻击; 2)控制输出通过无线通信网络与执行器传输数据时会遭受攻击。假设系统遭受DoS攻击后的测量输出和控制输出变为
系统的测量输出为
| $ \tilde{\boldsymbol{y}}_{i, k}=\alpha_k \boldsymbol{C}_2 \boldsymbol{x}_{i, k}+\boldsymbol{D}_2 \boldsymbol{\varpi}_{i, k} $ | (3) |
式中αk∈{0, 1}为服从Bernoulli分布的白色序列。当DoS攻击发生时,αk=0,传感器测量数据丢失,可定义传感器通道丢包率表示为
| $ \left\{\begin{array}{l} \operatorname{Pr}\left\{\alpha_k=1\right\}=\mathrm{E}\left\{\alpha_k\right\}=\bar{\alpha} \\ \operatorname{Pr}\left\{\alpha_k=0\right\}=1-\mathrm{E}\left\{\alpha_k\right\}=1-\bar{\alpha} \end{array}\right. $ | (4) |
DoS攻击下基于状态观测器的系统状态方程为
| $ \hat{\boldsymbol{x}}_{i, k+1}=\boldsymbol{A} \hat{\boldsymbol{x}}_{i, k}+\boldsymbol{B}_1 \tilde{\boldsymbol{u}}_{i, k}+\boldsymbol{L}\left(\tilde{\boldsymbol{y}}_{i, k}-\bar{\alpha} \boldsymbol{C}_2 \hat{\boldsymbol{x}}_{i, k}\right) $ | (5) |
控制协议为
| $ \left\{\begin{array}{l} \tilde{\boldsymbol{u}}_{i, k}=\beta_k \hat{\boldsymbol{u}}_{i, k} \\ \hat{\boldsymbol{u}}_{i, k}=\boldsymbol{K} \sum\limits_j^N a_{i j}\left(\hat{\boldsymbol{x}}_{j, k}-\hat{\boldsymbol{x}}_{i, k}\right) \end{array}\right. $ | (6) |
式中:
| $ \left\{\begin{array}{l} \operatorname{Pr}\left\{\boldsymbol{\beta}_k=1\right\}=\mathrm{E}\left\{\boldsymbol{\beta}_k\right\}=\overline{\boldsymbol{\beta}} \\ \operatorname{Pr}\left\{\boldsymbol{\beta}_k=0\right\}=1-\mathrm{E}\left\{\boldsymbol{\beta}_k\right\}=1-\overline{\boldsymbol{\beta}} \end{array}\right. $ | (7) |
由状态估计方程可得系统估计误差为
| $ \boldsymbol{e}_{i, k}=\boldsymbol{x}_{i, k}-\hat{\boldsymbol{x}}_{i, k} $ | (8) |
对于N个智能体,引入以下描述:
| $ \left\{\begin{array}{l} \boldsymbol{x}_k=\left(\boldsymbol{x}_{1, k}, \boldsymbol{x}_{2, k}, \cdots, \boldsymbol{x}_{N, k}\right)^{\mathrm{T}} \\ \boldsymbol{e}_k=\left(\boldsymbol{e}_{1, k}, \boldsymbol{e}_{2, k}, \cdots, \boldsymbol{e}_{N, k}\right)^{\mathrm{T}} \\ \boldsymbol{\varpi}_k=\left(\boldsymbol{\varpi}_{1, k}, \boldsymbol{\varpi}_{2, k}, \cdots, \boldsymbol{\varpi}_{N, k}\right)^{\mathrm{T}} \\ \boldsymbol{z}_k=\left(\boldsymbol{z}_{1, k}, \boldsymbol{z}_{2, k}, \cdots, \boldsymbol{z}_{N, k}\right)^{\mathrm{T}} \end{array}\right. $ | (9) |
结合式(1)、(3)、(5)、(6)、(8)、(9),并通过应用Kronecker乘积得到DoS攻击下基于状态观测器的多智能体ICPS方程为
| $ \left\{\begin{aligned} \boldsymbol{x}_{k+1}= & \left(\boldsymbol{A}_1-\boldsymbol{S}_1\right) \boldsymbol{x}_k+\boldsymbol{S}_1 \boldsymbol{e}_k-\left(\boldsymbol{\beta}_k-\overline{\boldsymbol{\beta}}\right) \boldsymbol{S}_2 \boldsymbol{x}_k+ \\ & \left(\boldsymbol{\beta}_k-\overline{\boldsymbol{\beta}}\right) S_2 e_k+S_3 \boldsymbol{\varpi}_k \\ \boldsymbol{z}_k= & \left(\boldsymbol{I}_N \otimes \boldsymbol{C}_1\right) \boldsymbol{x}_k+\left(I_N \otimes \boldsymbol{D}_1\right) \boldsymbol{\varpi}_k \\ \boldsymbol{e}_{k+1}= & \boldsymbol{S}_4 \boldsymbol{e}_k-\left(\alpha_k-\bar{\alpha}\right) \boldsymbol{S}_5 x_k+\boldsymbol{S}_6 \boldsymbol{\varpi}_k \end{aligned}\right. $ | (10) |
式中:A1=IN⊗A,S1=M⊗(βB1K),S2=M⊗(B1K),S3=IN⊗B2,S4=IN⊗(A-α-LC2),S5=IN⊗(LC2),S6=IN⊗(B2-LD2)。
2 优化指标及博弈框架定义1 系统(10)是均方指数稳定的,如果存在φ>0,τ∈(0, 1)满足:
| $ \mathrm{E}\left\{\left\|\boldsymbol{\varphi}_k\right\|^2\right\} \leqslant \boldsymbol{\varphi} \tau^k \mathrm{E}\left\{\left\|\boldsymbol{\varphi}_0\right\|^2\right\} $ | (11) |
式中,
为抑制干扰对系统的影响,对干扰的增长率加以约束,即引入干扰抑制水平γ,则对于干扰抑制水平γ>0,系统满足H∞一致性有如下定义。
定义2 如果多智能体下ICPS的被控输出和干扰满足式(12),则系统在满足H∞性能约束条件下达到一致性,即满足H∞一致性约束:
| $ \sum\limits_{k=0}^T \mathrm{E}\left\{\sum\limits_{i=1}^N\left\|z_{i, k}\right\|^2\right\}<\gamma^2 \sum\limits_{k=0}^T \mathrm{E}\left\{\sum\limits_{i=1}^N\left\|\boldsymbol{\varpi}_{i, k}\right\|^2\right\} $ | (12) |
式中: T为有限域长度,对于干扰抑制水平γ,定义系统稳定的裕度为γΔ1=γmax-γ,表示距离系统不稳定时干扰抑制水平允许变化的宽裕程度; γmax为系统稳定时允许的最大干扰抑制水平。从相对稳定性的角度分析,稳定裕度越大,则说明系统在面对环境变化时容错率越高,系统相对稳定性越强。
对于存在干扰的多智能体下ICPS,系统输入和外部干扰可看作是冲突双方,而博弈论主要研究冲突模式下的最优策略。因此为设计更具鲁棒性能的H∞一致性最优控制器,可将外部干扰和系统输入建立为两人零和博弈模型,则对于优化性能函数为
| $ \begin{aligned} \boldsymbol{J}_\gamma(\boldsymbol{\mu}, \boldsymbol{\omega})= & \sum\limits_{k=0}^{T-1}\left(\boldsymbol{x}_{i, k}^{\mathrm{T}} \boldsymbol{Q}_k \boldsymbol{x}_{i, k}+\boldsymbol{u}_{i, k}^{\mathrm{T}} \boldsymbol{R}_k \boldsymbol{u}_{i, k}-\right. \\ & \left.\gamma^2 \boldsymbol{\varpi}_{i, k}^{\mathrm{T}} \boldsymbol{\varpi}_{i, k}\right)+\boldsymbol{x}_{i, T}^{\mathrm{T}} \boldsymbol{Q}_{\mathrm{f}} \boldsymbol{x}_{i, T} \end{aligned} $ | (13) |
式中:γ>0为干扰抑制水平,Qk、Rk为适当维度的正定权重矩阵,控制器(最小化玩家)期望性能函数最小,而干扰(最大化玩家)则希望这个函数最大。对于智能体i,控制策略μ ∈ Ω,μ=(μ0, μ1, …, μT-1),干扰策略ω∈W,ω=(ω0, ω1, …, ωT-1),则{Jγ: Ω, W}表示零和博弈空间。
考虑式(13)下的零和博弈问题有解,则需满足式(14)有解。
| $ \inf \limits_{\boldsymbol{\mu} \in \boldsymbol{\varOmega}} \sup \limits_{\boldsymbol{\omega} \in \boldsymbol{W}} \boldsymbol{J}_\gamma(\boldsymbol{\mu}, \boldsymbol{\omega})=\sup \limits_{\boldsymbol{\omega} \in \boldsymbol{W}} \inf \limits_{\boldsymbol{\mu} \in \boldsymbol{\Omega}} \boldsymbol{J}_\gamma(\boldsymbol{\mu}, \boldsymbol{\omega}) $ | (14) |
则博弈问题等同于求解干扰抑制水平γ的最小值,使得零和博弈问题有相等的上确界和下确界,这意味着零和博弈的鞍点解适用于最坏情况的控制器设计。对于策略对(μ, ω),有Jγ(μ*, ω)≤Jγ(μ*, ω*)≤Jγ(μ, ω*),则策略对(μ*, ω*)构成鞍点解。零和博弈值为Jγ(μ*, ω*)。
为使得γ在满足H∞一致性的条件下取得最小,利用上述零和博弈模型研究干扰抑制水平γ的凸优化问题:min γ。使γ最小化意味着系统不仅在满足式(12)的条件下达到H∞一致性,且为最坏情况下的最优H∞控制。结合系统H∞一致性约束条件和零和博弈理论对干扰抑制水平的约束目标,可概括为基于零和博弈的最优H∞一致性设计框架为
| $ \left\{\begin{array}{l} \sum\limits_{k=0}^T \mathrm{E}\left\{\sum\limits_{i=1}^N\left\|z_{i, k}\right\|^2\right\}<\gamma^2 \sum\limits_{k=0}^T \mathrm{E}\left\{\sum\limits_{i=1}^N\left\|\boldsymbol{\varpi}_{i, k}\right\|^2\right\} \\ \min \gamma \end{array}\right. $ | (15) |
当DoS攻击发生时,系统需综合考虑攻击造成的数据包丢失、一致性遭到破坏等问题,本文利用LMI给出系统在DoS攻击下达到指数均方稳定和H∞一致性需满足的条件。
3.1 稳定性分析引理1[20] 定义Lyapunov函数为V(φk),如果存在实标量λ≥0,η>0,ξ>0和0 < χ < 1满足:
| $ \eta\left\|\boldsymbol{\varphi}_k\right\|^2 \leqslant V\left(\boldsymbol{\varphi}_k\right) \leqslant \xi\left\|\boldsymbol{\varphi}_k\right\|^2 $ | (16) |
| $ \mathrm{E}\left\{V\left(\boldsymbol{\varphi}_{k+1}\right) \mid \boldsymbol{\varphi}_k\right\}-V\left(\boldsymbol{\varphi}_k\right) \leqslant \lambda-\chi V\left(\boldsymbol{\varphi}_k\right) $ | (17) |
则φk满足:
| $ \mathrm{E}\left\{\left\|\boldsymbol{\varphi}_k\right\|^2\right\} \leqslant \frac{\xi}{\eta}\left\|\boldsymbol{\varphi}_0\right\|^2(1-\chi)^k+\frac{\lambda}{\eta \chi} $ | (18) |
由引理1,本文给出系统满足均方指数稳定的充分条件。
定理1 对于控制增益K和观测器增益L,在干扰为0时,系统(10)是均方指数稳定的,如果存在正定矩阵 P1、P2需满足:
| $ \mathit{\pmb{\Theta}}_1^{\mathrm{T}} \mathit{\pmb{\Psi}}_1 \boldsymbol{\Theta}_1+\mathit{\pmb{\Theta}}_2^{\mathrm{T}}\mathit{\pmb{\Psi}}_2 \mathit{\pmb{\Theta}}_2-\mathit{\pmb{\Psi}}_1<0 $ | (19) |
式中:
证明 定义Lyapunov泛函为
| $ V_k=\boldsymbol{x}_k^{\mathrm{T}} \boldsymbol{P}_1 \boldsymbol{x}_k+\boldsymbol{e}_k^{\mathrm{T}} \boldsymbol{P}_2 \boldsymbol{e}_k $ | (20) |
由系统(10)可知:
| $ \begin{aligned} & \left.\mathrm{E}\left\{V_{k+1} \mid \boldsymbol{\varphi}_k\right\}-V_k=\mathrm{E}\right\}\left[\left(\boldsymbol{A}_1-\boldsymbol{S}_1\right) x_k+\boldsymbol{S}_1 \boldsymbol{e}_k-\right. \\ & \left.\left(\boldsymbol{\beta}_k-\overline{\boldsymbol{\beta}}\right) \boldsymbol{S}_2 \boldsymbol{x}_k+\left(\boldsymbol{\beta}_k-\overline{\boldsymbol{\beta}}\right) \boldsymbol{S}_2 \boldsymbol{e}_k\right]^{\mathrm{T}} \boldsymbol{P}_1\left[\left(\boldsymbol{A}_1-\boldsymbol{S}_1\right) \boldsymbol{x}_k+\right. \\ & \left.\boldsymbol{S}_1 \boldsymbol{e}_k-\left(\boldsymbol{\beta}_k-\overline{\boldsymbol{\beta}}\right) \boldsymbol{S}_2 \boldsymbol{x}_k+\left(\boldsymbol{\beta}_k-\overline{\boldsymbol{\beta}}\right) \boldsymbol{S}_2 \boldsymbol{e}_k\right]+\left[\boldsymbol{S}_4 \boldsymbol{e}_k-\right. \\ & \left.\left.\left(\alpha_k-\bar{\alpha}\right) \boldsymbol{S}_5 \boldsymbol{x}_k\right]^{\mathrm{T}} \boldsymbol{P}_2\left[\boldsymbol{S}_4 \boldsymbol{e}_k-\left(\alpha_k-\bar{\alpha}\right) \boldsymbol{S}_5 \boldsymbol{x}_k\right]\right\}- \\ & \boldsymbol{x}_k^{\mathrm{T}} \boldsymbol{P}_1 \boldsymbol{x}_k-\boldsymbol{e}_k^{\mathrm{T}} \boldsymbol{P}_2 \boldsymbol{e}_k \end{aligned} $ | (21) |
注意到
| $ \begin{aligned} & \mathrm{E}\left\{V_{k+1} \mid \boldsymbol{\varphi}_k\right\}-V_k= \\ & {\left[\left(\boldsymbol{A}_1-\boldsymbol{S}_1\right) \boldsymbol{x}_k+\boldsymbol{S}_1 \boldsymbol{e}_k\right]^{\mathrm{T}} \boldsymbol{P}_1\left[\left(\boldsymbol{A}_1-\boldsymbol{S}_1\right) \boldsymbol{x}_k+\boldsymbol{S}_1 \boldsymbol{e}_k\right]+} \\ & {\left[\boldsymbol{S}_4 \boldsymbol{e}_k\right]^{\mathrm{T}} \boldsymbol{P}_2\left[\boldsymbol{S}_4 \boldsymbol{e}_k\right]+(1-\bar{\alpha}) \bar{\alpha}\left[\left(\boldsymbol{S}_5 \boldsymbol{x}_k\right)^{\mathrm{T}} \boldsymbol{P}_2\left(\boldsymbol{S}_5 \boldsymbol{x}_k\right)\right]+} \\ & (1-\overline{\boldsymbol{\beta}}) \overline{\boldsymbol{\beta}}\left[\boldsymbol{S}_2 \boldsymbol{x}_k+\boldsymbol{S}_2 \boldsymbol{e}_k\right]^{\mathrm{T}} \boldsymbol{P}_1\left[\boldsymbol{S}_2 \boldsymbol{x}_k+\boldsymbol{S}_2 \boldsymbol{e}_k\right]- \\ & \boldsymbol{x}_k^{\mathrm{T}} \boldsymbol{P}_1 \boldsymbol{x}_k-\boldsymbol{e}_k^{\mathrm{T}} \boldsymbol{P}_2 \boldsymbol{e}_k=\boldsymbol{\varphi}_k^{\mathrm{T}} \mathit{\pmb{\Pi}} \boldsymbol{\varphi}_k \end{aligned} $ | (22) |
其中
| $ \begin{gathered} \mathit{\pmb{\Pi}}=\mathit{\pmb{\Gamma}}_1^{\mathrm{T}} \boldsymbol{P}_1 \mathit{\pmb{\Gamma}}_1+\mathit{\pmb{\Gamma}}_2^{\mathrm{T}} \boldsymbol{P}_2 \mathit{\pmb{\Gamma}}_2+ \\ {\left[\begin{array}{cc} \boldsymbol{S}_2 & \boldsymbol{S}_2 \\ \boldsymbol{S}_5 & \mathit{\pmb{0}} \end{array}\right]^{\mathrm{T}}\left[\begin{array}{cc} \zeta^2 \boldsymbol{P}_1 & \mathit{\pmb{0}} \\ \boldsymbol{0} & \boldsymbol{\vartheta}^2 \boldsymbol{P}_2 \end{array}\right]\left[\begin{array}{cc} \boldsymbol{S}_2 & \boldsymbol{S}_2 \\ \boldsymbol{S}_5 & \mathit{\pmb{0}} \end{array}\right]-\left[\begin{array}{cc} \boldsymbol{P}_1 & \mathit{\pmb{0}} \\ \mathit{\pmb{0}} & \boldsymbol{P}_2 \end{array}\right]} \end{gathered} $ |
式中:
则对比式(19)可知Π < 0,从而得到:
| $ \mathit{\pmb{\Pi}}_k^{\mathrm{T}} \mathit{\pmb{\Pi}} \mathit{\pmb{\Pi}}_k \leqslant \lambda_{\min }(-\mathit{\pmb{\Pi}}) \mathit{\pmb{\Pi}}_k^{\mathrm{T}} \mathit{\pmb{\Pi}}_k<-h \boldsymbol{\varphi}_k^{\mathrm{T}} \boldsymbol{\varphi}_k $ | (23) |
式中:
则由式(23)可知:
| $ \mathrm{E}\left\{V_{k+1} \mid \boldsymbol{\varphi}_k\right\}-V_k<-h \boldsymbol{\varphi}_k^{\mathrm{T}} \boldsymbol{\varphi}_k<-\frac{h}{\delta} V_k $ | (24) |
令
下面由定理1的结论给出系统达到H∞一致性时控制增益和观测器增益满足的条件。
3.2 DoS攻击下H∞一致性分析定理2 对于多智能体ICPS的H∞一致性性能约束问题,在干扰抑制水平γ>0的前提下, 如果存在正定矩阵 P1、P2和任意非零的
| $\left[\begin{array}{cc} \mathit{\pmb{\Phi}}_{11} & * \\ \mathit{\pmb{\Phi}}_{21} & \mathit{\pmb{\Phi}}_{22} \end{array}\right]<0 $ | (25) |
式中:
| $ \begin{aligned} \mathit{\boldsymbol{\Phi}}_{11} & =\left[\begin{array}{ccc} -\boldsymbol{P}_1 & * & * \\ \mathit{\pmb{0}} & -\boldsymbol{P}_2 & * \\ \mathit{\pmb{0}} & \mathit{\pmb{0}} & -\gamma^2 \boldsymbol{I} \end{array}\right] \\ \mathit{\boldsymbol{\Phi}}_{21} & =\left[\begin{array}{ccc} \boldsymbol{A}_1-\boldsymbol{S}_1 & \boldsymbol{S}_1 & \boldsymbol{S}_3 \\ \mathit{\pmb{0}} & \boldsymbol{S}_4 & \boldsymbol{S}_6 \\ \boldsymbol{I}_N \otimes \boldsymbol{C}_1 & \mathit{\pmb{0}} & \boldsymbol{I}_N \otimes \boldsymbol{D}_1 \\ \zeta \boldsymbol{S}_2 & \zeta \boldsymbol{S}_2 & \mathit{\pmb{0}} \\ \boldsymbol{\vartheta} \boldsymbol{S}_5 & \mathit{\pmb{0}} & \mathit{\pmb{0}} \end{array}\right] \\ \mathit{\boldsymbol{\Phi}}_{22} & =\left[\begin{array}{ccccc} -\boldsymbol{P}_1^{-1} & * & * & * & * \\ \mathit{\pmb{0}} & -\boldsymbol{P}_2^{-1} & * & * & * \\ \mathit{\pmb{0}} & \mathit{\pmb{0}} & -\boldsymbol{I} & * & * \\ \mathit{\pmb{0}} & \mathit{\pmb{0}} & \mathit{\pmb{0}} & -\boldsymbol{P}_1^{-1} & * \\ \mathit{\pmb{0}} & \mathit{\pmb{0}} & \mathit{\pmb{0}} &\mathit{\pmb{0}} & -\boldsymbol{P}_2^{-1} \end{array}\right] \end{aligned} $ |
证明 由定理1中Lyapunov泛函和式(10)可知:
| $ $$ \begin{aligned} & \mathrm{E}\left\{V_{k+1}\right\}-\mathrm{E}\left\{V_k\right\}+\mathrm{E}\left\{\boldsymbol{z}_k^{\mathrm{T}} \boldsymbol{z}_k\right\}-\gamma^2 \mathrm{E}\left\{\boldsymbol{\varpi}_k^{\mathrm{T}} \boldsymbol{\varpi}_k\right\}= \\ & \mathrm{E}\left\{\boldsymbol{x}_{k+1}^{\mathrm{T}} \boldsymbol{P}_1 \boldsymbol{x}_{k+1}+\boldsymbol{e}_{k+1}^{\mathrm{T}} \boldsymbol{P}_2 \boldsymbol{e}_{k+1}\right\}-\mathrm{E}\left\{\boldsymbol{x}_k^{\mathrm{T}} \boldsymbol{P}_1 \boldsymbol{x}_k+\boldsymbol{e}_k^{\mathrm{T}} \boldsymbol{P}_2 \boldsymbol{e}_k\right\}+ \\ & \mathrm{E}\left\{\boldsymbol{z}_k^{\mathrm{T}} \boldsymbol{z}_k\right\}-\gamma^2 \mathrm{E}\left\{\mathit{\pmb{\varpi}}_k^{\mathrm{T}} \mathit{\pmb{\varpi}}_k\right\}= \\ & \mathrm{E}\left\{\left[\left(\mathit{\pmb{A}}_1-\mathit{\pmb{S}}_1\right) \mathit{\pmb{x}}_k+\mathit{\pmb{S}}_1 \mathit{\pmb{e}}_k-\left(\mathit{\pmb{\beta}}_k-\bar{\mathit{\pmb{\beta}}}\right) \mathit{\pmb{\beta}}_k-\bar{\mathit{\pmb{\beta}}}_2 \mathit{\pmb{x}}_k+\right.\right. \\ & \left.\left(\mathit{\pmb{\beta}}_k-\bar{\mathit{\pmb{\beta}}}\right) \boldsymbol{S}_2 \boldsymbol{e}_k+\boldsymbol{S}_3 \boldsymbol{\varpi}_k\right]^{\mathrm{T}} \boldsymbol{P}_1\left[\left(\boldsymbol{A}_1-S_1\right) \boldsymbol{x}_k+\boldsymbol{S}_1 \boldsymbol{e}_k-\right. \\ & \left.\left(\mathit{\pmb{\beta}}_k-\bar{\mathit{\pmb{\beta}}}\right) \boldsymbol{S}_2 \boldsymbol{x}_k+\left(\mathit{\pmb{\beta}}_k-\bar{\mathit{\pmb{\beta}}}\right) \boldsymbol{S}_2 \boldsymbol{e}_k+\boldsymbol{S}_3 \boldsymbol{\varpi}_k\right]+\left[\boldsymbol{S}_4 \boldsymbol{e}_k-\right. \\ & \left.\left(\mathit{\pmb{\alpha}}_k-\bar{\mathit{\pmb{\alpha}}}\right) \boldsymbol{S}_5 \boldsymbol{x}_k+\boldsymbol{S}_6 \boldsymbol{\varpi}_k\right]^{\mathrm{T}} \boldsymbol{P}_2\left[\boldsymbol{S}_4 \boldsymbol{e}_k-\right. \\ & \left.\left(\mathit{\pmb{\alpha}}_k-\bar{\mathit{\pmb{\alpha}}}\right) \boldsymbol{S}_5 \boldsymbol{x}_k+\boldsymbol{S}_6 \boldsymbol{\varpi}_k\right]-\boldsymbol{x}_k^{\mathrm{T}} \boldsymbol{P}_1 \boldsymbol{x}_k-\boldsymbol{e}_k^{\mathrm{T}} \boldsymbol{P}_2 \boldsymbol{e}_k+ \\ & {\left[\left(\boldsymbol{I}_N \otimes \boldsymbol{C}_1\right) \boldsymbol{x}_k+\left(\boldsymbol{I}_N \otimes \boldsymbol{D}_1\right) \boldsymbol{\varpi}_k\right]^{\mathrm{T}}\left[\left(\boldsymbol{I}_N \otimes \boldsymbol{C}_1\right) \boldsymbol{x}_k+\right.} \\ & \left.\left.\left(\boldsymbol{I}_N \otimes \boldsymbol{D}_1\right) \boldsymbol{\varpi}_k\right]-\gamma^2 \mathit{\pmb{\varpi}}_k^{\mathrm{T}} \mathit{\pmb{\varpi}}_k\right\}= \\ & \mathrm{E}\left\{\left[\begin{array}{c} \boldsymbol{\varphi}_k \\ \boldsymbol{\varpi}_k \end{array}\right]^{\mathrm{T}}\left[\begin{array}{cc} \mathit{\pmb{\Pi}}+\mathit{\pmb{\Pi}}_1 & \mathit{\pmb{\Pi}}_2 \\ \mathit{\pmb{\Pi}}_2^{\mathrm{T}} & \boldsymbol{\Pi}_3 \end{array}\right]\left[\begin{array}{l} \boldsymbol{\varphi}_k \\ \boldsymbol{\varpi}_k \end{array}\right]\right\} \end{aligned} $$ $ | (26) |
式中:
| $ \begin{aligned} & \boldsymbol{\varphi}_k=\left[\begin{array}{l} \boldsymbol{x}_k \\ \boldsymbol{e}_k \end{array}\right] \\ &\mathit{\pmb{\Pi}}_1=\left[\begin{array}{ll} \boldsymbol{I}_N \otimes \boldsymbol{C}_1 & \boldsymbol{0} \end{array}\right]^{\mathrm{T}}\left[\begin{array}{ll} \boldsymbol{I}_N \otimes \boldsymbol{C}_1 & \boldsymbol{0} \end{array}\right] \\ &\mathit{\pmb{\Pi}}_2=\mathit{\pmb{\Gamma}}_1^{\mathrm{T}} \boldsymbol{P}_1 \boldsymbol{S}_3+\mathit{\pmb{\Gamma}}_2^{\mathrm{T}} \boldsymbol{P}_2 \boldsymbol{S}_6+\left[\begin{array}{l} \boldsymbol{I}_N \otimes \boldsymbol{C}_1 \\ \boldsymbol{0} \end{array}\right]^{\mathrm{T}}\left(\boldsymbol{I}_N \otimes \boldsymbol{D}_1\right) \\ & \mathit{\pmb{\Pi}}_3=\boldsymbol{S}_3^{\mathrm{T}} \boldsymbol{P}_1 \boldsymbol{S}_3+\boldsymbol{S}_6^{\mathrm{T}} \boldsymbol{P}_2 \boldsymbol{S}_6+\left(\boldsymbol{I}_N \otimes \boldsymbol{D}_1\right)^{\mathrm{T}}\left(\boldsymbol{I}_N \otimes \boldsymbol{D}_1\right)-\gamma^2 \boldsymbol{I} \end{aligned} $ |
根据Schur引理及式(25)可得
| $ \left[\begin{array}{cc} \mathit{\pmb{\Pi}}+\mathit{\pmb{\Pi}}_1 & \mathit{\pmb{\Pi}}_2 \\ \mathit{\pmb{\Pi}}_2^{\mathrm{T}} & \mathit{\pmb{\Pi}}_3 \end{array}\right]<0 $ | (27) |
进而可从式(26)得到:
| $ \mathrm{E}\left\{V_{k+1}\right\}-\mathrm{E}\left\{V_k\right\}+\mathrm{E}\left\{\boldsymbol{z}_k^{\mathrm{T}} \boldsymbol{z}_k\right\}-\gamma^2 \mathrm{E}\left\{\boldsymbol{\varpi}_k^{\mathrm{T}} \boldsymbol{\varpi}_k\right\}<0 $ | (28) |
上述式子对k从0到T作求和运算并进行移项,可得
| $ \begin{array}{r}\sum\limits_{k=0}^T \mathrm{E}\left\{\left\|\boldsymbol{z}_k\right\|^2\right\}< \gamma^2 \sum\limits_{k=0}^T \mathrm{E}\left\{\left\|\boldsymbol{\varpi}_k\right\|^2\right\}+ \\ \mathrm{E}\left\{V_0\right\}-\mathrm{E}\left\{V_{T+1}\right\}\end{array} $ | (29) |
由于初始状态φ0= 0,且VT+1=
| $ \sum\limits_{k=0}^T \mathrm{E}\left\{\left\|z_k\right\|^2\right\}<\gamma^2 \sum\limits_{k=0}^T \mathrm{E}\left\{\left\|\boldsymbol{\varpi}_k\right\|^2\right\} $ | (30) |
对比式(12)即系统满足H∞一致性约束,定理得证。
3.3 最优一致性设计对于干扰抑制水平的约束,有如下引理:
引理2[6] 对于性能函数Jγ(μ, ω)和系统方程(10),则控制策略ui, k是严格凸的,当且仅当
| $ \gamma^2 \boldsymbol{I}-\boldsymbol{B}_2^{\mathrm{T}} \boldsymbol{Y}_{k+1} \boldsymbol{B}_2>0 $ | (31) |
式中: Yk+1,k∈[1, T]为满足下列黎卡提方程的解:
| $ $\begin{aligned} \boldsymbol{Y}_k= & \boldsymbol{A}^{\mathrm{T}} \boldsymbol{Y}_{k+1} \boldsymbol{B}_2\left[\gamma^2 \boldsymbol{I}-\boldsymbol{B}_2^{\mathrm{T}} \boldsymbol{Y}_{k+1} \boldsymbol{B}_2\right]^{-1} \boldsymbol{B}_2^{\mathrm{T}} \boldsymbol{Y}_{k+1} \boldsymbol{A}+ \\ & \boldsymbol{A}^{\mathrm{T}} \boldsymbol{Y}_{k+1} \boldsymbol{A}+\boldsymbol{Q}_k\end{aligned}$ $ | (32) |
| $ \boldsymbol{Y}_{T+1}=\boldsymbol{Q}_{\mathrm{f}} $ | (33) |
注意到定理2中LMI式(25)中参数是非耦合的,则可通过反向递推黎卡提方程式(32)求解最小干扰抑制水平,联合求解LMI式(25),从而求得控制策略,达到最优H∞一致性控制的设计目的, 见算法1。
算法1 最优H∞一致性控制器设计
给定:α、β、T、Qk、Qf、M
输出:Υk、γ、K、L
算法步骤:
① 设置迭代次数为T,初始化k=T,ΥT+1=Qf;
② 如果式(19)成立,则进入步骤③,若不满足,则跳转至步骤⑦;
③ 如果条件(25)满足,则说明通过LMI式(25)求解控制增益和观测器增益是合理的,进行下一步对γ的约束计算,否则跳转至步骤⑦;
④ 求解反向递归黎卡提方程(33),得到 Υk、γ;
⑤ 如果γ满足式(31),则进行下一步,否则,令k=k-1,返回步骤④,继续循环迭代;
⑥ 由γ,通过求解LMI式(25)获得最优H∞一致性控制器,该算法可行。
⑦ 该算法不可行。
4 结果与分析对于不同的ICPS控制对象,若系统参数可有效辨识,即可采用本文控制算法求解最优一致性策略。
4.1 仿真对象本文采用不间断电源(uninterruptible power supply, UPS)作为被控对象,UPS的主要作用是为负载提供持续稳定的电力,目前UPS已广泛应用于医疗/生命支持、计算机、通讯设备和工厂生产的供电中。因此,保证UPS的鲁棒性和稳定性至关重要。
而在大型工厂中,往往存在多条工业生产线需要控制,如何保持多个UPS在供电时的一致性和稳定性成为关键问题。故在本文中,将研究由4个UPS控制工厂生产线的一致性控制问题,验证所设计的基于状态观测器下的H∞一致性最优控制策略能够使得系统在存在干扰和DoS攻击导致信号丢失的情况下,具有较强的H∞一致性。
对于由4个UPS组成的多智能体ICPS,N=4,考虑两种不同的通信拓扑结构分别见图 2、3。

|
图 2 Laplacian矩阵为M1的无向通信图 Fig. 2 Undirected communication graph with Laplacian matrix M1 |

|
图 3 Laplacian矩阵为M2的无向通信图 Fig. 3 Undirected communication graph with Laplacian matrix M2 |
无向图对应的Laplacian矩阵分别为:
| $ \boldsymbol{M}_1=\left[\begin{array}{cccc}3 & -1 & -1 & -1 \\ -1 & 2 & -1 & 0 \\ -1 & -1 & 3 & -1 \\ -1 & 0 & -1 & 2\end{array}\right] $ | (34) |
| $ \boldsymbol{M}_2=\left[\begin{array}{cccc}2 & 0 & -1 & -1 \\ 0 & 2 & -1 & -1 \\ -1 & -1 & 3 & -1 \\ -1 & -1 & -1 & 3\end{array}\right] $ | (35) |
单一UPS内部的信息物理融合过程如图 4所示,其他UPS将发生的状态信息传输给受控对象,受控对象将接收到的状态信息连同自身状态信息进行采集、传输、处理后产生决策信息,并将此决策信息传输给控制端,执行器接受决策指令并改变受控对象状态,并将信息返回其他UPS,如此循环交互。

|
图 4 内部信息物理融合过程 Fig. 4 Internal cyber-physical fusion process |
离散时间模型参数矩阵如下[21]:
| $ A=\left[\begin{array}{ccc}0.9226 & -0.6330 & 0 \\ 1.0 & 0 & 0 \\ 0 & 1.0 & 0\end{array}\right] $ | (36) |
| $ \boldsymbol{B}_1=\left[\begin{array}{l}1 \\ 0 \\ 0\end{array}\right] $ | (37) |
| $ \boldsymbol{B}_2=\left[\begin{array}{c}0.5 \\ 0 \\ 0.2\end{array}\right] $ | (38) |
| $ \boldsymbol{C}_1=\left[\begin{array}{lll}0.1 & 0 & 0\end{array}\right] $ | (39) |
| $ \boldsymbol{C}_2=\left[\begin{array}{lll}23.738 & 20.287 & 0\end{array}\right] $ | (40) |
| $ \boldsymbol{D}_1=0.1 $ | (41) |
| $ \boldsymbol{D}_2=0.2 $ | (42) |
对于最优H∞一致性控制的设计,首先选择矩阵Q = Qk= Qf=0.1 I, 采用粒子群搜索算法,求得γ*=2.317,之后分别对不同拓扑结构的情况下进行仿真,考虑不同DoS攻击强度对系统的影响,并采用文献[18]中基于事件触发的一致性控制方法作为对比试验。
假设采用本文算法求得的控制器增益和观测器增益分别记为K和L,采用文献[18]中算法,取干扰抑制水平γd=2.508,求得控制器增益记为 K ′,分别计算当Laplacian矩阵为M1、M2,系统遭受不同的DoS攻击强度时的控制器增益和观测器增益。表 1给出了攻击强度较小,即α =β=0.9时和攻击强度增大,即α=β=0.7时,在不同Laplacian矩阵下的控制器增益和观测器增益。
| 表 1 控制增益和观测器增益 Tab. 1 Controller gain and observer gain |
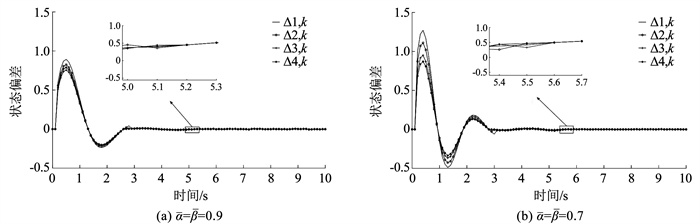
验证所设计的一致性协议在不同拓扑结构和不同攻击强度下的有效性,仿真结果见图 5、6。由图 5、6可知,在Laplacian矩阵为M1和M2时,系统状态在波动后达到一致,满足一致性。随着攻击强度增大,系统状态波动变大,且达到一致的时间更长,但仍能达到一致性。由此可见,本文设计的算法,使得系统在不同拓扑结构下遭受DoS攻击时,均满足一致性,且随着攻击强度增大,系统仍能保持一致性。

|
图 5 Laplacian矩阵为M1时在不同丢包率下采用本文算法的一致性仿真图 Fig. 5 Consensus simulation diagram of proposed algorithm under different packet loss rates when Laplacian matrix is M1 |
|
图 6 Laplacian矩阵为M2时在不同丢包率下采用本文算法的一致性仿真图 Fig. 6 Consensus simulation diagram of proposed algorithm under different packet loss rates when Laplacian matrix is M2 |
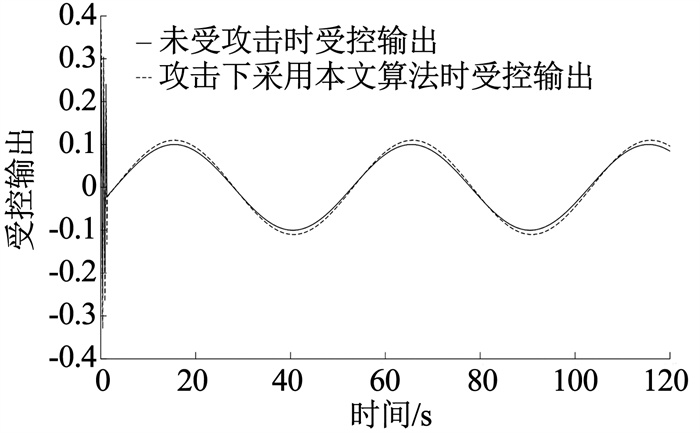
为验证状态与估计状态的误差有界性,在Laplacian矩阵为M1、α =β =0.7时,取平均估计误差为

|
图 7 平均估计误差仿真曲线 Fig. 7 Average estimation error simulation curve |
|
图 8 受控输出曲线 Fig. 8 Controlled output curve |
从一致性角度。在DoS攻击下,采用文献[18]算法的一致性仿真曲线如图 9、10所示,当攻击强度较小时,系统仍能满足一致性,随着攻击强度增大,系统不再满足一致性,表 2给出了采用两种算法下的定量比较,假设在同一Laplacian矩阵M1和相同攻击强度α =β=0.9下,本文控制算法下和文献[18]算法下系统状态达到一致的时间分别为4.6、7.1 s,在攻击下不同状态波动的最大误差值分别为0.132 6、0.705 9, 相较于文献[18]设计的控制方法,本文设计的控制算法使得系统各个状态变化幅度更小,达到一致的时间也更短。
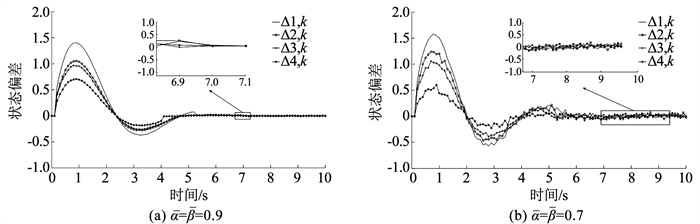
|
图 9 Laplacian矩阵为M1时在不同丢包率下采用文献[18]算法的一致性仿真图 Fig. 9 Consensus simulation diagram of Ref.[18] algorithm under different packet loss rates when Laplacian matrix isM1 |

|
图 10 Laplacian矩阵为M2时在不同丢包率下采用文献[18]算法的一致性仿真图 Fig. 10 Consensus simulation diagram of Ref. [18] algorithm under different packet loss rates when Laplacian matrix is M2 |
| 表 2 采用不同算法时的性能指标对比 Tab. 2 Comparison of performance metrics when different algorithms are used |
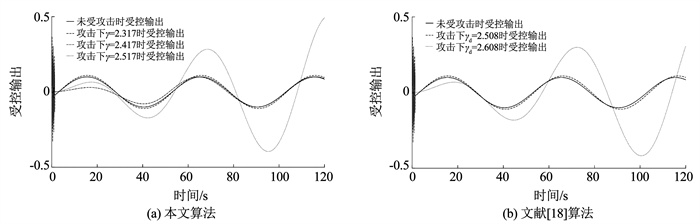
从相对稳定性角度。γΔ1=γmax-γ*,文献[18]算法下稳定裕度为γΔ2=
|
图 11 不同γ下受控输出曲线 Fig. 11 Controlled output curve under different γ |
1) 根据多智能体中单个智能体能够感知环境、执行动作影响环境的特点,将ICPS中执行器、传感器、被控对象描述为智能体,构建固定拓扑的多智能体ICPS模型,解决多个被控对象组成的ICPS的模型构建问题。
2) 考虑双通道DoS攻击下系统通信信道堵塞等因素的影响,基于状态观测器对估计后的状态进行一致性控制协议的设计,提高设计的准确度,并构建包括系统误差、状态变量、受控输出在内的更具一般性的整体系统模型,解决一类DoS攻击建模问题。
3) 利用零和博弈方法,将控制器和外部扰动视为博弈中的参与者,解决干扰抑制水平的优化问题,并通过求解反向递归黎卡提方程和线性矩阵不等式,设计最优H∞一致性控制方案,提高一致性控制设计的精度。
4) 以4个不间断电源的控制问题作为仿真对象,通过Matlab软件进行仿真验证。结果表明,在不同拓扑结构和不同攻击强度的DoS攻击下,本文设计的最优H∞一致性控制能使系统状态满足一致性,并且系统受控输出有较好的相对稳定性。
| [1] |
LIU Bin, CHEN Jingzhao, HU Yong. Mode division-based anomaly detection against integrity and availability attacks in industrial cyber-physical systems[J]. Computers in Industry, 2022, 137: 103609. DOI:10.1016/j.compind.2022.103609 |
| [2] |
DING Derui, HAN Qinglong, XIANG Yang, et al. A survey on security control and attack detection for industrial cyber-physical systems[J]. Neurocomputing, 2018, 275: 1674. DOI:10.1016/j.neucom.2017.10.009 |
| [3] |
孙子文, 张炎棋. 工业信息物理系统的攻击建模研究[J]. 控制与决策, 2019, 34(11): 2323. SUN Ziwen, ZHANG Yanqi. Research on attack modeling of industrial cyber physical systems[J]. Control and Decision, 2019, 34(11): 2323. DOI:10.13195/j.kzyjc.2018.1796 |
| [4] |
SUN Qi, ZHANG Kunwu, SHI Yang. Resilient model predictive control of cyber-Physical systems under DoS attacks[J]. IEEE Transactions on Industrial Informatics, 2020, 16(7): 4920. DOI:10.1109/TⅡ.2019.2963294 |
| [5] |
刘珊, 黎善斌, 胥布工. 混合攻击下时变信息物理系统的有限时域H∞控制[J]. 控制理论与应用, 2020, 37(2): 331. LIU Shan, LI Shanbin, XU Bugong. Finite horizon H∞ control for time-varying cyber-physical system under hybrid attacks[J]. Control Theory & Applications, 2020, 37(2): 331. DOI:10.7641/CTA.2019.80703 |
| [6] |
庞岩, 王娜, 夏浩. 基于博弈论的信息物理融合系统安全控制[J]. 自动化学报, 2019, 45(1): 185. PANG Yan, WANG Na, XIA Hao. A game theory approach for secure control of cyber-physical systems[J]. Acta Automatica Sinica, 2019, 45(1): 185. DOI:10.16383/j.aas.2018.c180365 |
| [7] |
薛威峰, 孙子文. 数据注入攻击下ICPS的自适应事件触发弹性控制[J]. 控制理论与应用, 2024, 41(5): 866. XUE Weifeng, SUN Ziwen. Adaptive event triggered resilient control of ICPS under data injection attack[J]. Control Theory & Applications, 2024, 41(5): 866. DOI:10.7641/CTA.2023.20774 |
| [8] |
ZHANG Chunlei, YANG Guanghong, LU Anyang. Resilient observer-based control for cyber-physical systems under denial-of-service attacks[J]. Information Sciences, 2021, 545: 102. DOI:10.1016/j.ins.2020.07.070 |
| [9] |
ZHANG Dan, WANG Qingguo, FENG Gang, et al. A survey on attack detection, estimation and control of industrial cyber-physical systems[J]. ISA Transactions, 2021, 116: 1. DOI:10.1016/j.isatra.2021.01.036 |
| [10] |
MAHMOUD M S, HAMDAN M M, BAROUDI U A. Modeling and control of cyber-physical systems subject to cyber attacks: a survey of recent advances and challenges[J]. Neurocomputing, 2019, 338: 101. DOI:10.1016/j.neucom.2019.01.099 |
| [11] |
TAYLOR J M, SHARIF H R. Security challenges and methods for protecting critical infrastructure cyber-physical systems[C]//2017 International Conference on Selected Topics in Mobile and Wireless Networking (MoWNeT). Avignon: IEEE, 2017: 1. DOI: 10.1109/MoWNet.2017.8045959
|
| [12] |
赵红专, 孙棣华, 程森林, 等. 一种离散连续混成的时空事件驱动的CPS体系架构[J]. 哈尔滨工业大学学报, 2016, 48(9): 170. ZHAO Hongzhuan, SUN Dihua, CHENG Senlin, et al. A hybrid discrete and continuous CPS architecture driven by spatial-temporal event[J]. Journal of Harbin Institute of Technology, 2016, 48(9): 170. DOI:10.11918/j.issn.0367-6234.2016.09.029 |
| [13] |
AMATO A, QUARTO A, DI LECCE V. An application of cyber-physical system and multi-agent technology to demand-side management systems[J]. Pattern Recognition Letters, 2021, 141: 23. DOI:10.1016/j.patrec.2020.09.004 |
| [14] |
XUE Shuangsi, LI Huan, CAO Hui, et al. Distributed edge-event-triggered consensus of multi-agent system under DoS attack[J]. Pattern Recognition Letters, 2023, 174: 118. DOI:10.1016/j.patrec.2023.08.015 |
| [15] |
CHEN Runze, LI Yuanxin, HOU Zhongsheng. Distributed model-free adaptive control for multi-agent systems with external disturbances and DoS attacks[J]. Information Sciences, 2022, 613: 309. DOI:10.1016/j.ins.2022.09.035 |
| [16] |
LI Yongming, TONG Shaocheng. Bumpless transfer distributed adaptive backstepping control of nonlinear multi-agent systems with circular filtering under DoS attacks[J]. Automatica, 2023, 157: 111250. DOI:10.1016/j.automatica.2023.111250 |
| [17] |
ZHANG Dan, LIU Lu, FENG Gang. Consensus of heterogeneous linear multiagent systems subject to aperiodic sampled-data and DoS attack[J]. IEEE Transactions on Cybernetics, 2019, 49(4): 1501. DOI:10.1109/TCYB.2018.2806387 |
| [18] |
WANG Shenquan, ZHAO Changbei, ZHANG Bangcheng, et al. Event-triggered based security consensus control for multi-agent systems with DoS attacks[J]. Neurocomputing, 2022, 505: 214. DOI:10.1016/j.neucom.2022.07.033 |
| [19] |
LI Xiaomeng, ZHOU Qi, LI Panshuo, et al. Event-triggered consensus control for multi-agent systems against false data-injection attacks[J]. IEEE Transactions on Cybernetics, 2020, 50(5): 1856. DOI:10.1109/TCYB.2019.2937951 |
| [20] |
WANG Zidong, YANG Fuwen, HO D W C, et al. Robust H∞ control for networked systems with random packet losses[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2007, 37(4): 916. DOI:10.1109/TSMCB.2007.896412 |
| [21] |
YUAN Yuan, ZHU Quanyan, SUN Fuchun, et al. Resilient control of cyber-physical systems against Denial-of-Service attacks[C]//2013 6th International Symposium on Resilient Control Systems (ISRCS). San Francisco: IEEE, 2013: 54. DOI: 10.1109/ISRCS.2013.6623750
|
 2024, Vol. 56
2024, Vol. 56


