2. 上海市动力工程多相流动与传热重点实验室(上海理工大学),上海 200093
2. Shanghai Key Laboratory of Multiphase Flow and Heat Transfer in Power Engineering (University of Shanghai for Science and Technology), Shanghai 200093, China
随着全球能源安全和气候问题加剧,世界范围内各国亟需推动能源转型。与传统能源相比,新能源资源丰富、再生可持续、环境友好,具有较大的发展潜力。风电作为一种清洁的新型能源,具有很高的环保价值。海上风力机多分布在近海区域,海上风电布置日益密集的同时,船舶与其碰撞的风险也逐渐提高,因此,研究海上风力机碰撞的动态响应对降低风力机受损和事故损失具有重要意义。据Global offshore Wind Health and Safety Organization统计数据显示2020年全年共发生743起近海风电事故,其中178起为船舶事故,高风险潜在事故占比高达37.5%[1]。Christensen等[2]综合考虑风电场分布区域、航线位置分布以及船舶航向等因素对船舶-海上风力机碰撞概率的影响,指出在5年周期内,风力机受船舶碰撞频率达0.21。因此研究海上风力机防护装置对海上风力机安全稳定运行具有重要意义。
国内外学者先后对船舶-风力机碰撞问题进行研究。Ding等[3]利用ABAQUS模拟不同船速下重力式基础风力机与船舶碰撞,得出结论:撞击能量耗散主要以过渡段塑性变形为主,且大面积损伤会出现于该区域。Biehl等[4]使用LS-DYNA软件分别模拟单桩、导管架及单立柱三桩基础风力机与不同类船舶碰撞,结果表明导管架结构具有最佳抗撞击性能,并指出单立柱三桩基础风力机碰撞研究需进行进一步开展。刘宇航等[5]利用3种不同类型风力机进行碰撞模拟,并对塔架动力响应与损伤进行分析,指出对风力机增设防护装置的必要性。Moulas等[6]通过ABAQUS对导管架风力机进行碰撞模拟,得到的结果显示碰撞过程中在基础X型焊接节点处最容易出现变形。
上述研究主要针对风力机基础损伤分析,但缺乏相应的防护措施,基于此诸多学者提出了不同类型的防护装置,旨在改善风力机的安全性和可靠性。赵鑫磊等[7]提出一种设孔海上风力机防护装置,并模拟对比不同布孔策略下防护性能差异,结果显示采用边与内壁切向平行策略布置孔可有效降低最大接触力。Han等[8]等用不同材料设计4种类型防护装置,LS-DYNA模拟结果显示泡沫铝材料应用于防护装置能显著其防护性能,泡沫铝和橡胶组成的双层防护装置能更有效地抑制碰撞过程中塔顶动态响应。Ren等[9]等模拟3 MW海上风力机单桩基础受2×106 kg船舶碰撞的动力过程,提出了一种钢球壳的防撞装置,研究其抗撞性能,球型防护装置可以平滑接触面,通过自身结构塑性变形,降低塔顶结构的动力响应,减少风力机损伤,且球型设计可有效使船舶在非正面碰撞发生后改变方向远离基础,正向、侧向撞击下均有较好表现。
现有对风力机防护装置研究主要集中分布于不同材料类型和简单结构变换,少见关于防护装置结构深入的研究。Yue等[10]基于相切圆定理提出了一种开有分形孔洞结构的橡胶防护装置,模拟船舶撞击三桩基础风力机,与传统实心防护装置相比,分形防护装置具有更好的防撞吸能特性,并指出一阶分形结构有利于防护装置吸收更多能量。本文基于分形仿生理论设计一种新型防护装置,并探究其防护性能,以期为海上风力机防护研究提供设计参考。
1 基础理论 1.1 控制方程船舶与风力机碰撞为一个瞬态过程,其控制方程可表示如下:
| $ \boldsymbol{M a}(t)+\boldsymbol{C} \boldsymbol{v}(t)+\boldsymbol{K} x(t)=\boldsymbol{F}(t)+\boldsymbol{H}(t) $ | (1) |
式中: M为质量矩阵,C为阻尼矩阵,K为刚度矩阵,F(t)为结构承受的碰撞力,H(t)为沙漏力,a(t)、v(t)、x(t)分别为t时刻的加速度、速度和位移。
1.2 钢本构模型Q235具有良好的抗海水冲刷腐蚀特性,故常被用于作为海上风力机与出船舶材料[11-12];风力机塔架材料依据文献[13]选用Q345钢。采用Cowper-Symonds模型[14-15]对Q235、Q345进行描述, 能较好地反映出应变率效应,材料名义屈服强度与抗拉强度和应变率成正相关。为更好地模拟冲击载荷下材料的特性,在LS-DYNA中基于该模型关系式建立了非线性弹塑性材料模型,表达式为[16]
| $ \sigma_y=\left[1+(\dot{\varepsilon} / C)^{1 / p}\right]\left(\sigma_0+\beta E_P \varepsilon_{\text {eff }}^p\right) $ | (2) |
式中: σy为最大屈服应力,σ0为初始屈服应力,EP为塑性强化模量,
Q235钢和Q345钢材料参数见表 1。表中:ρ为材料密度,υ为泊松比,E为弹性模量,Et为切线模量,ε为失效应变。
| 表 1 材料Q235和Q345参数 Tab. 1 Material parameters of Q235 and Q345 |
本文选用Ogden橡胶本构模型作为防护主体材料,模型表达式为[17]
| $ W=\sum\limits_i^N\left(2 \mu_i / \alpha_i^2\right)\left(\lambda_1^{\alpha_i}+\lambda_2^{\alpha_i}-2\right) $ | (3) |
式中: W为应变能函数, αi、μi为材料常数,其取值见表 2;λ1、λ2为主伸长率。
| 表 2 Ogden模型材料参数 Tab. 2 Material parameters of Ogden |
分形是一门新兴的学科,它由前人观察大自然中的许多景观以及分子和原子的无规则运动而发展而来。分形学科跨越多个领域,推动人类对自然规律和物理本质的理解。分形即在简单的空间中由复杂点集合组成的结构,这些结构具有以下两个主要特性[18]:
1) 空间填充性。整体上呈现出不规则但具有精细结构的特点。从数学角度来定义,分形的维度大于拓扑维度。
2) 自相似性。即整体与部分之间存在一定的相似比例关系。
这些特性使得分形独具魅力,并广泛应用于多个学科领域,包括物理学、数学、生物学、化学等。通过研究分形,人们能够更深入地理解自然界中的复杂性,并探索其中隐藏的规律和原理。图 1为几种传统分形结构。
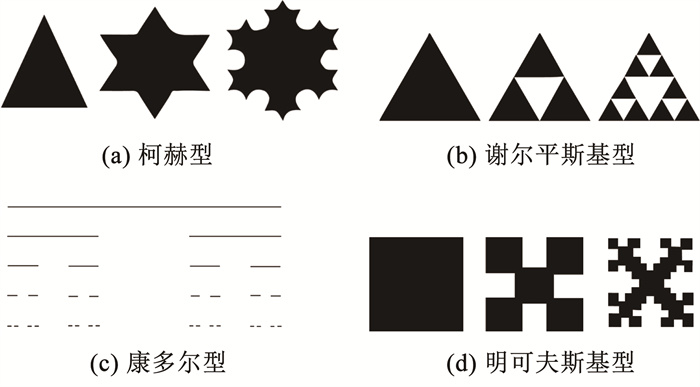
|
图 1 传统分形结构 Fig. 1 Traditional fractal structure |
由于分形结构的特性,诸多学者将分形理论用于结构设计,以及对大自然中存在的分形结构进行仿生应用。Zhang等[19]通过迭代构造2种阶数分形自相似正六边形层次蜂巢,基于该结构所开展飞机外壁耐撞性研究表明:分形结构可显著提高吸能能力。Wang等[20]基于柯赫型分形提出一种分形抗压薄壁,通过试验和仿真,研究不同柯赫型分形阶数和壁厚的单壁和双壁混合柯赫型分形设计的碰撞性能,结果表明:混合柯赫型结构中存在显著的协同效应,基于柯赫型分形截面的薄壁结构可显著提升抗撞性。Zhang等[21]基于蛛网等结构,提出了一种分形的分层六边形结构吸能装置,通过试验和仿真,研究了分形阶数及形状对抗撞性的影响,结果表明:分层及分形结构均能显著改善原结构的吸能效果,分形阶数、几何参数显著影响结构的能量耗散率,在给定质量下,二维阶数设计最优。Wu等[22]提出了一种树状分形防护结构,通过试验和仿真方法对三角形、方形和五角形的树状分形抗撞性能进行研究,与单壁结构相比,树状分形结构在提高比能吸收和碰撞力效率方面具有较大潜力,其中三阶树状分形结构承载能力最佳。
2.2 防护装置结构设计诸多学者对于叶脉仿生结构进行研究,发现其具有优秀的吸能特性。Xing等[23]研究了叶脉的分布规律,并通过仿生树叶的设计最大化表面体积比来改进板状结构,设计了基于叶脉调控的工作台结构,并通过有限元模拟和试验进行了验证。结果显示,与常规工作台相比,仿生设计工作台的平均位移降低了33.9%。Gao等[24]根据叶脉结构重新排列了机床立柱的内部加劲筋,并设计了一种仿生立柱。通过仿真和试验与常规柱进行对比,发现仿生柱的最大变形显著降低,前六阶固有频率也有显著提升。He等[25]借鉴了荷叶叶脉分枝结构,提出了一种新型的能量吸收结构。通过有限元仿真和试验对比验证,结果表明新型结构可以更有效地吸收冲击能量,其吸能特性与几何参数密切相关。本文采取的仿生对象为王莲,王莲叶片呈圆形或卵形,尺寸宽大,具有极大承载能力,可较大程度抵抗外部载荷,此外王莲叶脉具有明显分形特征,基于此提出一种王莲叶脉仿生风力机防护桩,并建立简化仿生分形模型(见图 2)。

|
图 2 王莲叶脉分形结构简化设计 Fig. 2 Simplified design of victoria vein fractal structure |
结构从具有分形点的1阶分支开始,由分形点形成两个分支,得到2阶结构,从每个新分支取一个新的分形点,在每个分形点上生成两个新分支,得到3阶分形结构,随后可以通过同样的方法对树状分形设计进行无限扩展。使用分形系数来描述分形点位置:
| $ \delta_N=\frac{l_2^1}{l_1^1}=\frac{l_2^2}{l_1^1}=\cdots=\frac{l_2^N}{l_1^N} $ | (4) |
式中:l1N、l2N分别为分形点前、后分支长度。
考虑实际应用及工艺需求,选定3阶分形阶数,建立分形结构如图 3所示,通过阵列得到仿生王莲形式分形结构,分支长度均为1.5 m,夹角大小为30°,将草图展平与成型至防护装置钢壳,防护装置高度为7.5 m,内层主体防护材料内、外径分别为5.0、7.7 m;外层钢壳厚度为0.1 m,分形叶脉结构厚度为0.05 m,结构模型见图 4。

|
图 3 分形结构的建立 Fig. 3 Establishment of fractal structure |
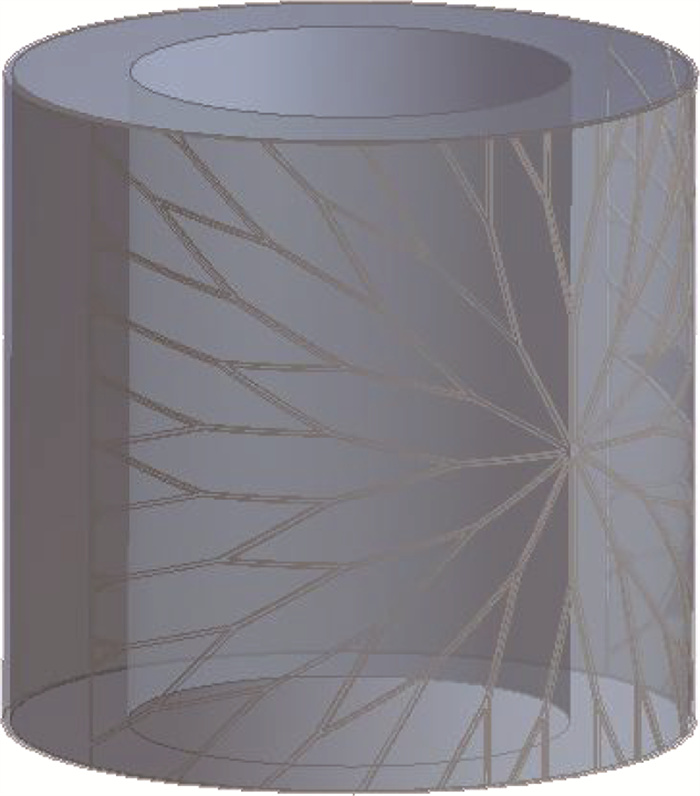
|
图 4 仿生防护装置示意 Fig. 4 Schematic diagram of biomimetic protective device |
风力机由叶片、机舱、轮毂、电机系统以及基础塔架组成,其中塔架包括横撑、筒体、钢管桩和斜撑组成。本文采用国内某4 MW单立柱三桩海上风力机为研究对象,结构尺寸参数详见表 3[26]。
| 表 3 单立柱三桩基础尺寸参数 Tab. 3 Geometry of tripod support structure |
单立柱三桩基础与土层耦合情况采取p-y曲线法[27]来描述,采用地下16 m土层特性可较好地模拟桩柱周围土层本构特性,p-y曲线见图 5。轮毂、电气系统及叶片远离碰撞区域,故采取集中质量法集中在塔顶机舱处[28]。风力机有限元模型如图 6所示,碰撞接触受力区域网格加密,网格尺寸大小为0.2 m;塔架立柱上下部分的尺寸为0.4 m,桩柱、横斜及斜撑等远离碰撞区域网格尺寸均为0.6 m。

|
图 5 16 m土层的p-y曲线 Fig. 5 Soil p-y curve of 16 m depth |
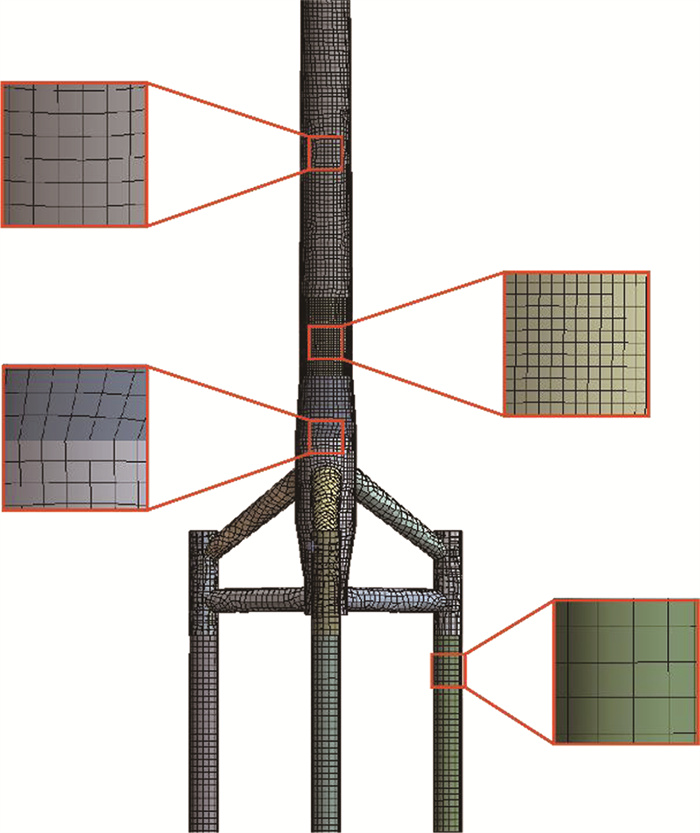
|
图 6 有限元模型 Fig. 6 FEM of tripod |
撞击船舶选用常见的前倾型艏船舶模型,船艏为碰撞区域,对其网格进行加密,其网格尺寸为0.2 m,船身船尾区域网格尺寸为0.6 m,船舶具体参数见表 4,图 7为其有限元模型。船舶与海水之间的相互作用不可忽视,通过附加质量法对其进行简化,不仅可以节省计算资源、提高计算效率,亦可保证模拟结果的精确性,基于船舶碰撞方向为正向碰撞,碰撞船舶附加质量系数取5%[29]。
| 表 4 船舶主要参数 Tab. 4 Main parameters of vessel |

|
图 7 船舶有限元模型 Fig. 7 FEM of ship |
对于复杂的仿生分形结构,需要对防护装置网格进行局部细化,仿生王莲叶脉分形部分网格尺寸细化为0.05 m,其他部分网格尺寸为0.20 m,有限元模型见图 8。

|
图 8 仿生防护装置有限元模型 Fig. 8 Finite element model of biomimetic protective device |
防护装置主体防护材料选用Ogden橡胶,在LS-DYNA中分别建立防护装置主体材料与风力机基础、主体材料及仿生叶脉钢壳、船舶与外层钢壳的接触模型,均使用AUTOMATIC_SURFACE_ TO_SURFACE模型。保证其他外界条件相同,建立同等尺寸但不含仿生分形叶脉结构防护装置仿真与之进行对比。
4 结果及分析 4.1 沙漏能验证LS-DYNA模拟碰撞过程中单元通常会由于集中载荷产生沙漏,沙漏易导致网格变形为锯齿状,结构响应周期大幅缩短,干扰计算过程。为避免沙漏作用影响结果准确性,要求沙漏能占比低于总能5%。图 9为模拟仿生分形防护装置及对比模型沙漏能占比,最大值均低于5%,计算结果均满足要求[30-31]。
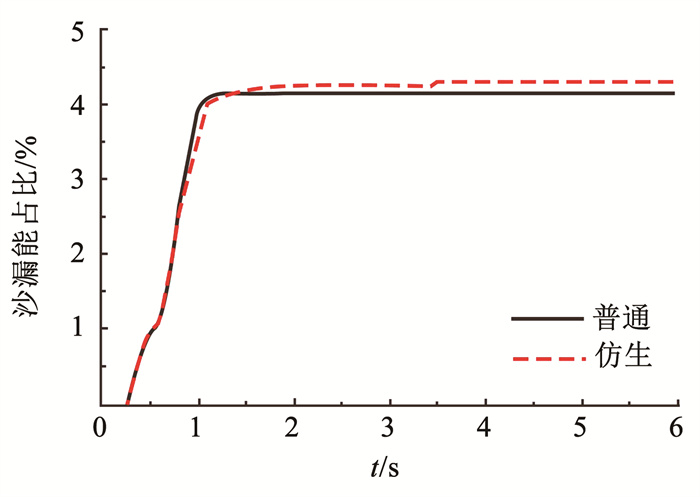
|
图 9 沙漏能占比 Fig. 9 Proportion of hourglass energy |
图 10为两种防护装置保护下风力机受撞后接触力曲线,二者曲线变化存在明显差异,对于普通防护装置,碰撞发生前接触力为0,接触发生后曲线迅速上升,随后主体防护材料发挥防护作用,接触力增速明显减慢,缓慢升至最高值23.94 MN后,船舶进入离开防护装置的过程,接触力迅速下降至0。对于仿生分形防护装置,碰撞发生后接触力增速稍慢,升至第1个峰值22.87 MN后,钢壳外层材料部分失效,接触力先下降至19.53 MN,随后在仿生叶脉部分及主体防护材料的共同主要防护作用下,接触力逐渐升至最大值22.97 MN,最后较缓慢下降至0。较普通防护装置,仿生叶脉防护装置可起到降低最大接触力的作用。

|
图 10 接触力对比 Fig. 10 Comparison of contact forces |
图 11分别为普通防护装置及仿生分形防护装置保护下风力机基础在0.3、0.6、0.9、1.2 s的应力云图。与普通防护装置相比,仿生防护装置接触区域高应力区域范围更小,仅有立柱与基础连接处应力较大。0.6 s时即仿生防护装置保护下接触力第1次达峰值时应力比普通防护装置大,但整体最大应力更低。

|
图 11 风力机塔架应力云图 Fig. 11 Stress contour map of wind turbine tower |
单独提取立柱与基础连接高应力区域单元应力曲线如图 12所示,两种防护装置保护下,连接处单元应力曲线均出现大幅度震荡现象,应力在接触发生后,迅速升至最大值,随后防护装置产生作用,应力曲线逐渐降低,在碰撞结束后,风力机塔架产生晃动,应力随之升高后继续波动。对比两种防护装置,普通防护装置及仿生分形防护装置连接处最大应力分别为440.5、363.7 MPa,且平均应力明显降低,仿生结构可提升防护装置对立柱与基础连接处的防护能力。

|
图 12 连接处应力曲线图 Fig. 12 Stress curve diagram of joint |
船舶撞击单立柱三桩基础模拟中,存在能量的转化过程。船舶的初始动能会转化为船舶与风力机之间的内能、阻尼能、接触中的滑移能以及由于变形而积累的沙漏能。图 13展示了在普通防护装置和仿生分形防护装置下的系统能量曲线。

|
图 13 系统总能量曲线图 Fig. 13 Total energy curve of system |
船舶与风力机基础接触前,总动能稳定不变。船舶与风力机接触后动能迅速降低,而内能则呈现相反的趋势迅速增加。船舶与防护装置的面对面接触会产生滑移能和阻尼能,而沙漏形变则会产生沙漏能。当船舶与风力机开始分离时,即系统动能达到最低点之后,动能曲线会反弹,而内能曲线则下降。完全分离后,由于惯性作用,风力机往往会产生往复运动和轻微振荡,动能和内能相互转化。在阻尼作用下,风力机会经历自由衰减运动,而沙漏形变也会逐渐累积,导致系统阻尼能和沙漏能的增加。整个过程中,系统的总能量保持不变,符合能量守恒定律。
仿生分形防护装置保护下系统内能吸收最高值较普通防护装置提升6.2%,为9.43 MJ,吸能速度较快。此外仿生分形防护0装置保护下系统动能曲线回弹后最高点为5.01 MJ,内能曲线下降最低点为4.36 MJ,而普通防护装置分别为5.50、3.20 MJ,仿生结构使回弹最大动能下降10.0%、内能耗散率提升10.2%。
为探究仿生结构对防护装置内能转化的影响,防护装置主体材料及钢壳内能变化曲线见图 14。随碰撞发生,普通防护装置的钢壳及主体材料内能曲线呈较稳定的上升趋势至峰值,随后下降至一稳定数值,该稳定数值即材料耗散内能,吸收内能峰值分别为0.30、2.90 MJ,耗散内能分别为0.10、0.31 MJ。仿生防护装置内能曲线存在明显波动,外部钢壳内能曲线上升速度较普通防护装置更快,于0.6 s达第1次峰值0.90 MJ,经一小段下降后再次上升至第2个峰值0.98 MJ,随后下降至耗散内能0.63 MJ;主体橡胶材料内能曲线在上述相同时间亦存在波动,吸收内能峰值为2.56 MJ,耗散内能为0.21 MJ。
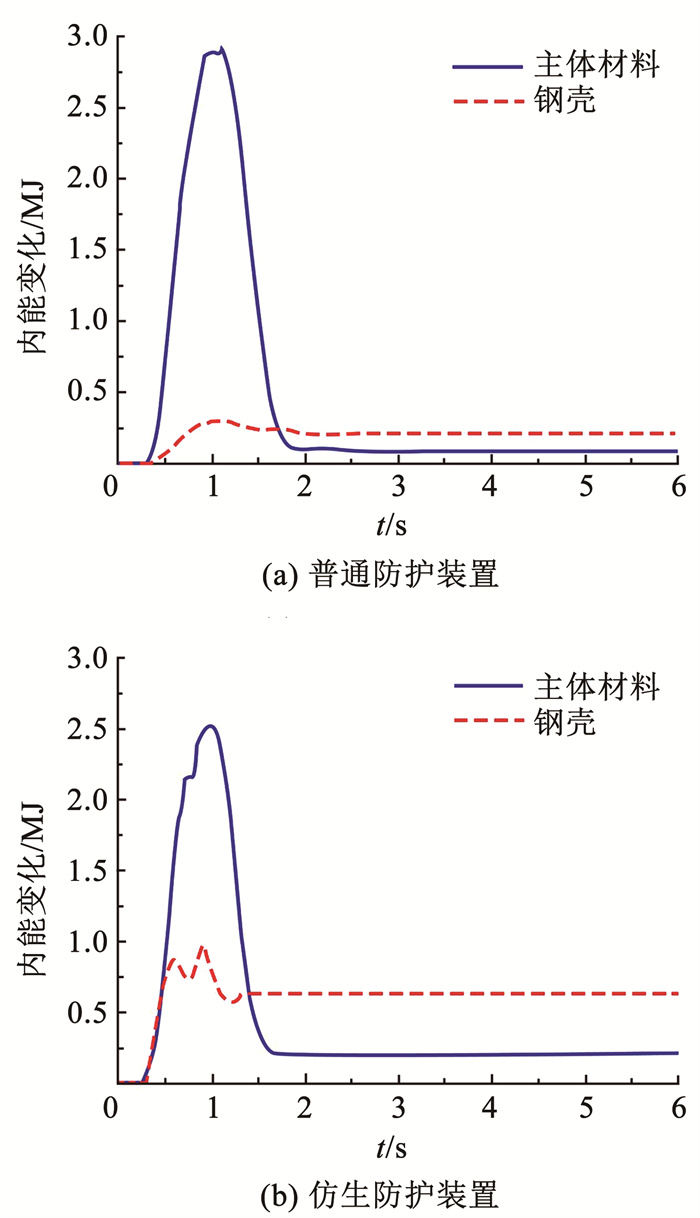
|
图 14 防护装置内能曲线 Fig. 14 Internal energy curve of protective device |
较普通防护装置,仿生分形防护装置主体防护材料内能最大值下降,但能量耗散数值提升,钢壳吸能效果显著提升,且能量耗散率提升31.29%,表 5为内能曲线峰值及耗散统计表。
| 表 5 内能曲线峰值及耗散统计表 Tab. 5 Peak value and dissipation statistics table of internal energy curve |
内能曲线波动与接触力曲线波动存在相似趋势,这是由于在变形过程中外部钢壳首先出现损伤,叶脉结构同时提升主体材料及钢壳钢护面积导致主体材料能量耗散值提升,钢壳材料能量耗散率提升。
5 结论1) 普通防护装置及仿生分形防护装置最大接触力分别为23.94、22.97 MN,仿生叶脉结构可起到降低最大接触力的作用。
2) 较普通防护装置,仿生防护装置接触区域高应力区域范围更小,且整体最大应力更低。
3) 仿生叶脉结构可以提升防护装置对立柱与基础连接处的防护能力,普通防护装置及仿生分形防护装置连接处最大应力分别为440.5、363.7 MPa,且平均应力明显降低。
4) 仿生分形防护使系统内能吸收最高值提升6.2%,吸能速度较快。此外仿生分形防护装置保护下系统动能曲线回弹后最高点为5.01 MJ,内能曲线下降最低点为4.36 MJ,而普通防护装置分别为5.50、3.20 MJ,仿生结构使回弹最大动能下降10.0%、内能耗散率提升10.2%。
5) 较普通防护装置,仿生分形防护装置主体防护材料内能最大值下降,但能量耗散数值提升,钢壳吸能效果显著提升,且能量耗散率提升31.29%。
| [1] |
Global Offshore Wind Health and Safety Organization. 2020 Incident Data Report[R/OL]. (2021-06-23). https://www.gplusoff-shorewind.com/work-programme/workstreams/statistics
|
| [2] |
CHRISTENSEN C, ANDERSEN L W, PEDERSEN P H. Ship collision risk for an offshore wind farm[J]. Structural Safety, 2001, 1. |
| [3] |
DING Hongyan, ZHU Qi, ZHANG Puyang. Dynamic simulation on collision between ship and offshore wind turbine[J]. Transactions of Tianjin University, 2014, 20(1): 1. DOI:10.1007/s12209-014-2133-x |
| [4] |
BIEHL F, LEHMANN E. Collisions of ships with offshore wind turbines: calculation and risk evaluation[M]//Offshore Wind Energy. Berlin: Springer, 2006: 281. DOI: 10.1007/978-3-540-34677-7_17
|
| [5] |
刘宇航, 李春, 周红杰, 等. 三种海上风力机支撑基础与船舶碰撞的动力响应分析[J]. 中国机械工程, 2019, 30(14): 1646. LIU Yuhang, LI Chun, ZHOU Hongjie, et al. Analysis of dynamic responses of collisions between three types of offshore wind turbine foundations and ship[J]. China Mechanical Engineering, 2019, 30(14): 1646. DOI:10.3969/j.issn.1004-132X.2019.014.002 |
| [6] |
MOULAS D, SHAFIEE M, MEHMANPARAST A. Damage analysis of ship collisions with offshore wind turbine foundations[J]. Ocean Engineering, 2017, 143: 149. DOI:10.1016/j.oceaneng.2017.04.050 |
| [7] |
赵鑫磊, 韩志伟, 李春, 等. 海上风力机设孔防护装置性能研究[J]. 中国电机工程学报, 2021, 41(16): 5624. ZHAO Xinlei, HAN Zhiwei, LI Chun, et al. Research on protection performance of via hole fender for offshore wind turbine[J]. Proceedings of the CSEE, 2021, 41(16): 5624. DOI:10.13334/j.0258-8013.pcsee.201426 |
| [8] |
HAN Zhiwei, LI Chun, DENG Yunhe, et al. The analysis of anti-collision performance of the fender with offshore wind turbine tripod impacted by ship and the coefficient of restitution[J]. Ocean Engineering, 2019, 194: 106614. DOI:10.1016/j.oceaneng.2019.106614 |
| [9] |
REN Nianxin, OU Jinping. A crashworthy device against ship-OWT collision and its protection effects on the tower of offshore wind farms[J]. China Ocean Engineering, 2009, 23(4): 593. |
| [10] |
YUE Xinzhi, HAN Zhiwei, LI Chun, et al. The study on structure design of fender of offshore wind turbine based on fractal feature during collision with ship[J]. Ocean Engineering, 2021, 236: 109100. DOI:10.1016/j.oceaneng.2021.109100 |
| [11] |
彭文山, 刘雪键, 刘少通, 等. 含砂流动海水中Q235钢冲刷腐蚀行为研究[J]. 表面技术, 2019, 48(9): 230. PENG Wenshan, LIU Xuejian, LIU Shaotong, et al. Erosion-corrosion behavior of Q235 steel in flowing seawater containing sand particles[J]. Surface Technology, 2019, 48(9): 230. DOI:10.16490/j.cnki.issn.1001-3660.2019.09.026 |
| [12] |
王艺陶, 冯国庆, 李陈峰, 等. 船用Q235钢裂纹扩展速率试验[J]. 哈尔滨工程大学学报, 2015, 36(10): 1302. WANG Yitao, FENG Guoqing, LI Chenfeng, et al. Crack propagation rate tests of marine steel Q235[J]. Journal of Harbin Engineering University, 2015, 36(10): 1302. DOI:10.11990/jheu.201407050 |
| [13] |
刘晨, 何建军, 王刚, 等. 塔筒钢在模拟海洋环境下的慢应变拉伸性能研究[J]. 太阳能学报, 2020, 41(2): 73. LIU Chen, HE Jianjun, WANG Gang, et al. Study on slow strain rate tensile properties of tower tube steel in simulated ocean environment[J]. Acta Energiae Solaris Sinica, 2020, 41(2): 73. DOI:10.19912/j.0254-0096.2020.02.011 |
| [14] |
孟利平, 程远征, 张伦平, 等. 应变率和应力三轴度对Q345B钢动态力学性能的影响研究[J]. 船舶力学, 2019, 23(10): 1210. MENG Liping, CHENG Yuanzheng, ZHANG Lunping, et al. Influence of strain rate and stress triaxiality on the dynamic mechanical behavior of Q345B steel[J]. Journal of Ship Mechanics, 2019, 23(10): 1210. DOI:10.3969/j.issn.1007-7294.2019.10.007 |
| [15] |
支旭东, 张荣, 林莉, 等. Q235B钢动态本构及在LS-DYNA中的应用[J]. 爆炸与冲击, 2018, 38(3): 596. ZHI Xudong, ZHANG Rong, LIN Li, et al. Dynamic constitutive model of Q235B steel and its application in LS-DYNA[J]. Explosion and Shock Waves, 2018, 38(3): 596. DOI:10.11883/bzycj-2016-0286 |
| [16] |
白金泽. LS-DYNA3D理论基础与实例分析[M]. 北京: 科学出版社, 2005. BAI Jinze. Theoretical basis and case analysis of LS-DYNA3D[M]. Beijing: Science Press, 2005. |
| [17] |
OGDEN R W. Non-linear elastic deformation[M]. New York: Dover Publications, Inc., 1997.
|
| [18] |
(波)伯努瓦·B·曼德布罗特. 大自然的分形几何学[M]. 上海: 上海远东出版社, 1998. MANDELBROT B B. The fractal geometry of nature[M]. Shanghai: Shanghai Far East Publishers, 1998. |
| [19] |
ZHANG Yong, LU Minghao, WANG C H, et al. Out-of-plane crashworthiness of bio-inspired self-similar regular hierarchical honeycombs[J]. Composite Structures, 2016, 144: 1. DOI:10.1016/j.compstruct.2016.02.014 |
| [20] |
WANG Jin, ZHANG Yong, HE Ning, et al. Crashworthiness behavior of Koch fractal structures[J]. Materials & Design, 2018, 144: 229. DOI:10.1016/j.matdes.2018.02.035 |
| [21] |
ZHANG Yong, WANG Jin, WANG Chunhui, et al. Crashworthiness of bionic fractal hierarchical structures[J]. Materials & Design, 2018, 158: 147. DOI:10.1016/j.matdes.2018.08.028 |
| [22] |
WU Jiacheng, ZHANG Yong, ZHANG Feng, et al. A bionic tree-liked fractal structure as energy absorber under axial loading[J]. Engineering Structures, 2021, 245: 112914. DOI:10.1016/j.engstruct.2021.112914 |
| [23] |
XING Denghai, CHEN Wuyi, ZHAO Ling, et al. Structural bionic design for high-speed machine tool working table based on distribution rules of leaf veins[J]. Science China Technological Sciences, 2012, 55(8): 2091. DOI:10.1007/s11431-012-4805-x |
| [24] |
GAO Hanjun, SUN Jianfei, CHEN Wuyi, et al. Structural bionic design for a machine tool column based on leaf veins[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2018, 232(16): 2764. DOI:10.1177/0954406217726565 |
| [25] |
HE Qiang, WANG Yonghui, SHI Xiaona, et al. Crushing behavior on the cylindrical tube based on lotus leaf vein branched structure[J]. Mechanics of Materials, 2022, 165: 104205. DOI:10.1016/j.mechmat.2021.104205 |
| [26] |
HAO Ertong, LIU Chunguang. Evaluation and comparison of anti-impact performance to offshore wind turbine foundations: Monopile, tripod, and jacket[J]. Ocean Engineering, 2017, 130: 218. DOI:10.1016/j.oceaneng.2016.12.008 |
| [27] |
APIRP. Recommended practice for planning, designing and constructing fixed offshore platforms-working stress design: 2A-WSD[S]. Washington: American Petroleum Institute, 2000
|
| [28] |
DNV-RP-C204. Design against accidental laods[S]. Hovik: Det Norske Veritas, 2010
|
| [29] |
李艳贞, 胡志强, 邹早建. 海上风电站遭遇船舶侧向撞击时的结构动力响应分析[J]. 振动与冲击, 2010, 29(10): 123. LI Yanzhen, HU Zhiqiang, ZOU Zaojian. Structural dynamic response analysis of an offshore wind turbine stricken by a ship in lateral direction[J]. Journal of Vibration and Shock, 2010, 29(10): 123. DOI:10.13465/j.cnki.jvs.2010.10.042 |
| [30] |
石少卿, 康建功, 汪敏, 等. ANSYS/LS-DYNA在爆炸与冲击领域内的工程应用[M]. 北京: 中国建筑工业出版社, 2011. SHI Shaoqing, KANG Jiangong, WANG Min, et al. Engineering application of ANSYS/LS-DYNA in the field of explosion and impact[M]. Beijing: China Architecture & Building, 2011. |
| [31] |
莫袁鸣. 金属-复合材料双层壁结构冰撞击响应与损伤研究[D]. 南京: 南京航空航天大学, 2018 MO Yuanming. Study on ice impact response and damage of metal-composite double wall structure[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2018. DOI: 10.27239/d.cnki.gnhhu.2019.000728 |
 2024, Vol. 56
2024, Vol. 56


