摘要
油气管道环焊缝自动化打磨因生产效率高、一致性好、安全可靠等优势成为打磨作业的重要发展方向。以控制打磨后焊缝余高为目的,使用Box-Behnken方法设计并进行实验,建立了材料去除面积和法向磨削力的预测模型,分析了磨具转速、磨削速度、下压深度对材料去除面积和法向磨削力的影响规律,提出了基于材料去除面积的焊缝磨削分层策略和工艺规划方法,建立了数学模型并设计了简单可视化的程序。结果表明:下压深度对材料去除面积的影响最大、磨具转速的影响最小,下压深度和磨具转速对法向磨削力的影响较大、对磨削速度的影响最小,并得出了最优工艺参数。建立的预测模型与实验吻合较好,最大误差分别为3.9%和6.8%。对提出的余高打磨策略进行验证,打磨后的焊缝余高与预期值误差最大为0.32 mm。
Abstract
Automated grinding of circumferential welds in oil and gas pipelines has become an important development direction due to its advantages of high productivity, good consistency and safety. With the purpose of controlling the residual height of the weld seam after grinding,Box-Behnken method was used to design experiments to establish the prediction model of material removal area and normal grinding force. The impact of rotational speed of abrasive tool, grinding speed, and downfeed depth on material removal area and normal grinding force was analyzed. A weld seam grinding stratification strategy and processing planning method were proposed. Moreover, a mathematical model was built and a simple visualization program was designed. The results show that the downfeed depth has the greatest influence on the material removal area, while the impact of grinding wheel speed is minimal. The downfeed depth and grinding wheel speed have a significant effect on the normal grinding force, while the influence of polishing speed is minimal.The optimal process parameters are derived.In addition, the established prediction model agrees well with the test results, with maximum error of 3.9% and 6.8% for material removal area and normal grinding force, respectively.The proposed residual grinding strategy is validated, and maximum deviation between the residual grinding height of weld seams and the expected value is maximum 0.32 mm.
随着我国经济规模不断攀升,各行各业对石油天然气等能源的需求迅速增长,而管道运输由于安全、规模大、不受气候影响等因素成为能源运输的重要方式之一[1]。目前,随着X80钢级别管线钢的生产技术日渐成熟,不断完善X80钢管线的生产工艺成为研究的主要方向[2]。油气管线的焊接过程中,熔池会由于重力驱动流向管道的底部,造成局部余高过高的现象,对定径、平头倒棱、防腐防护和成品检测等工序产生影响[3]。当前,此类焊缝打磨作业主要依靠工人手工进行,效率较低、余高一致性差且生产环境恶劣,对工人健康严重不利[4]。自动打磨系统由于生产效率高、一致性好、安全可靠的优势成为当前打磨作业的一个重要发展方向。
Zhu等[5]针对螺旋管焊缝,提出基于线激光传感器焊缝特征点识别的焊缝轨迹跟踪方法,并在工业机器人末端增加了二自由度直线运动平台和磨削工具,通过解耦控制简化了机器人轨迹规划算法。Wang等[6]用三维轮廓扫描仪将曲面和焊缝重构为点云数据,为磨削路径规划提供依据,结果表明重构误差在5.3%以内。Ren等[7]发现磨削过程中火花场面积、密度等特征值与材料去除率密切相关,提出了用于监测材料去除率的火花场测量方法。Yang等[8]考虑非均质接触轮的弹性变形,通过理论计算建立材料去除模型,确定了接触轮与工件接触面的压力分布,并从工艺参数的角度提高了磨削效率。Zhao等[9]通过实验,建立表面粗糙度预测模型,对磨料粒度、接触力、进给速度等参数进行优化,使用简化后的预测模型,达到了快速预测表面粗糙度的目的,显著提高了加工质量。
综上所述,学者们大多采用线激光传感器对焊缝表面建模[10],对模型分层并生成打磨路径。而实际加工过程中,由于磨具本身存在弹性,加工后尺寸往往与预期不符。部分学者也注意到这个问题,建立了考虑打磨头弹性变形的材料去除率模型,但计算过程复杂,无法应用到加工过程中。本文用单因素实验的方法,分析工艺参数的适用区间。采用Box-Behnken设计方法,分析工艺参数对材料去除量及磨削力的影响机理,建立考虑磨具自身柔性的预测模型。以控制打磨后焊缝余高为目的,基于响应面预测模型,提出基于材料去除面积的焊缝余高打磨自适应补偿策略。
1 实验
1.1 建立焊缝截面的数学模型
引入材料去除面积为打磨效率的衡量指标,建立如图1所示的焊缝数学模型,将焊缝截面轮廓简化为二次抛物线[11],其函数表达式为:
(1)
(2)
式中:w为焊缝宽度;H为焊缝余高。通过提取打磨前焊缝的宽度和高度,建立焊缝界面轮廓曲线,根据材料待去除高度h和磨削速度Vw,即可计算材料去除面积S和材料去除率MRR。
(3)
(4)
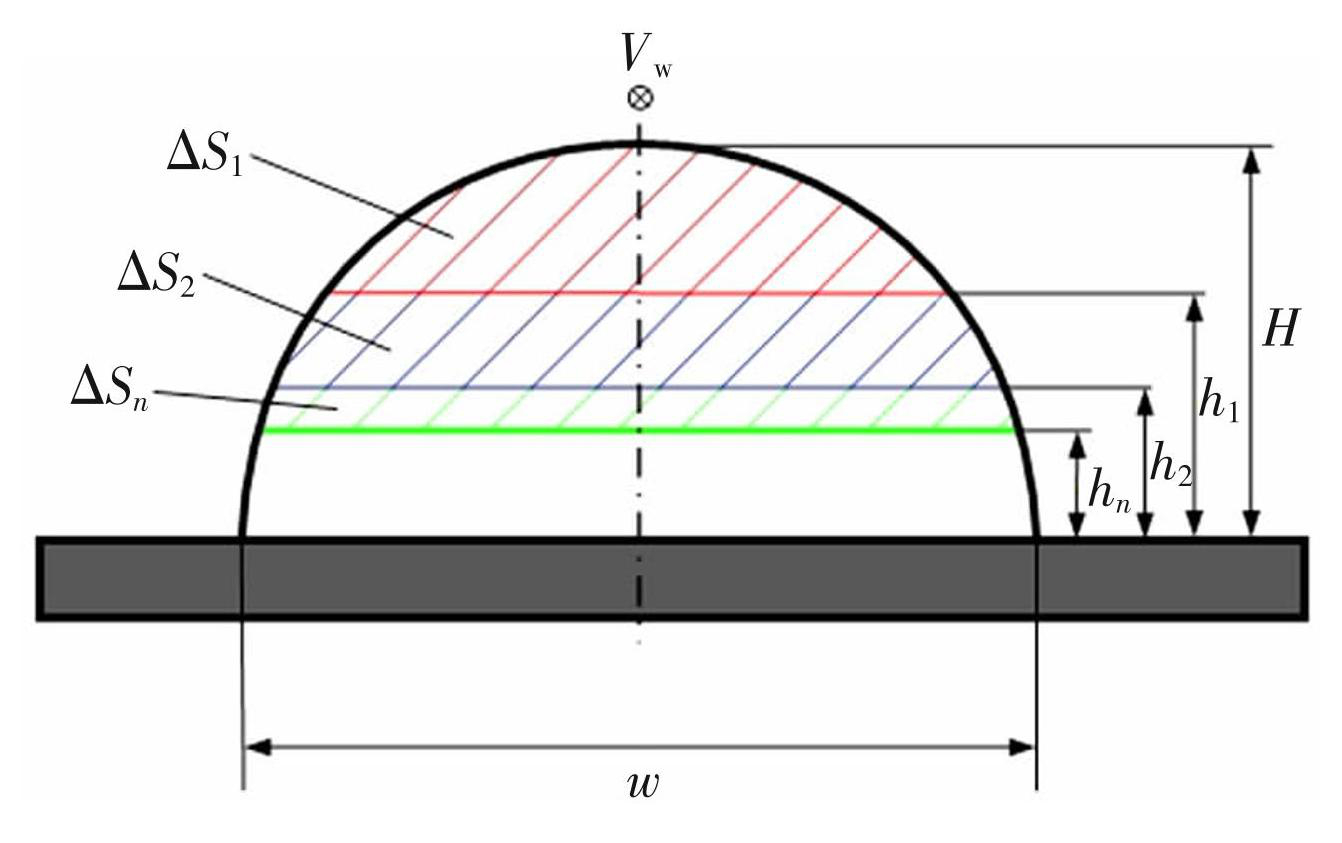
图1焊缝横截面数学模型
Fig.1Mathematical model of weld cross section
1.2 实验设备
在调查主要能源运输项目以及焊缝验收标准后发现,油气管道呈现出大口径、薄壁、高压力的特点[12],焊缝宽度15~25 mm,余高2~5 mm。对于大口径环焊缝,打磨头接触位置可近似为平面,因此,实验选用如图2所示直焊缝,w=23.5 mm,H=3.2 mm。通过二次曲线拟合后的函数表达式为
(5)

图2实验用直焊缝
Fig.2Direct weld for test: (a) the weld; (b) cross-section of the weld
实验中所用设备主要包括3部分。
1)数控加工系统:数控加工系统具有可靠性和通用性,广泛应用于各种加工过程中。本文采用五轴数控机床与打磨头结合的方式进行磨削实验,如图3所示。数控机床主要包括五轴联动机械装置和操控面板两部分,位置精度可达0.001 mm。

图3数控加工系统
Fig.3Numerical control processing system: (a) five-axis linkage; (b) control panel
2)测力仪:为了对磨削过程中的法向磨削力进行测量,将测力仪(9257B,Kistler)连接5070A电荷放大器和数据采集卡,磨削力数据由Dynoware软件处理。

图4Kistler测力仪
Fig.4Kistler moniergometer: (a) kistler force tester; (b) dynoware software
3)自适应补偿策略规划软件:开发了焊缝余高打磨自适应补偿工艺规划软件,分为定截面焊缝磨削参数输出及变截面焊缝磨削工艺规划两部分。主要由模型读取、等材料去除面积分层、预测模型设置、工艺规划、数据导出等模块组成。
1.3 工艺参数适用范围
1.3.1 磨削工具
数控打磨的末端执行机构由角磨机实现,通过实验,对不同常用磨具的材料去除能力及磨削效果进行对比分析,选用实验参数为:磨具转速n=9 000 r/min、磨削速度Vw=240 mm/min、下压深度Δh=3 mm。实验结果如图5所示,砂轮片的材料去除能力最佳,但法向磨削力最大,且磨削过程中出现大量划痕及表面烧伤的情况;百叶片在保证材料去除率的同时法向磨削力最小,且加工后表面光滑。因此,确定百叶片为后续实验工具。

图5不同磨削工具对比
Fig.5Comparison of different grinding tools: (a) material removal rate; (b) grinding effect of the grinding wheel; (c) grinding effect of louver blades
除了磨具类型,磨具的目数也对材料去除能力有着显著影响。实验表明,随着磨具目数的增加,磨具的打磨效率先增大后减小,而法向磨削力呈现出越来越大的趋势,且在目数大于120#后,出现了严重的表面氧化,如图6所示。在法向磨削力适中的前提下,80#的百叶片材料去除率最大。
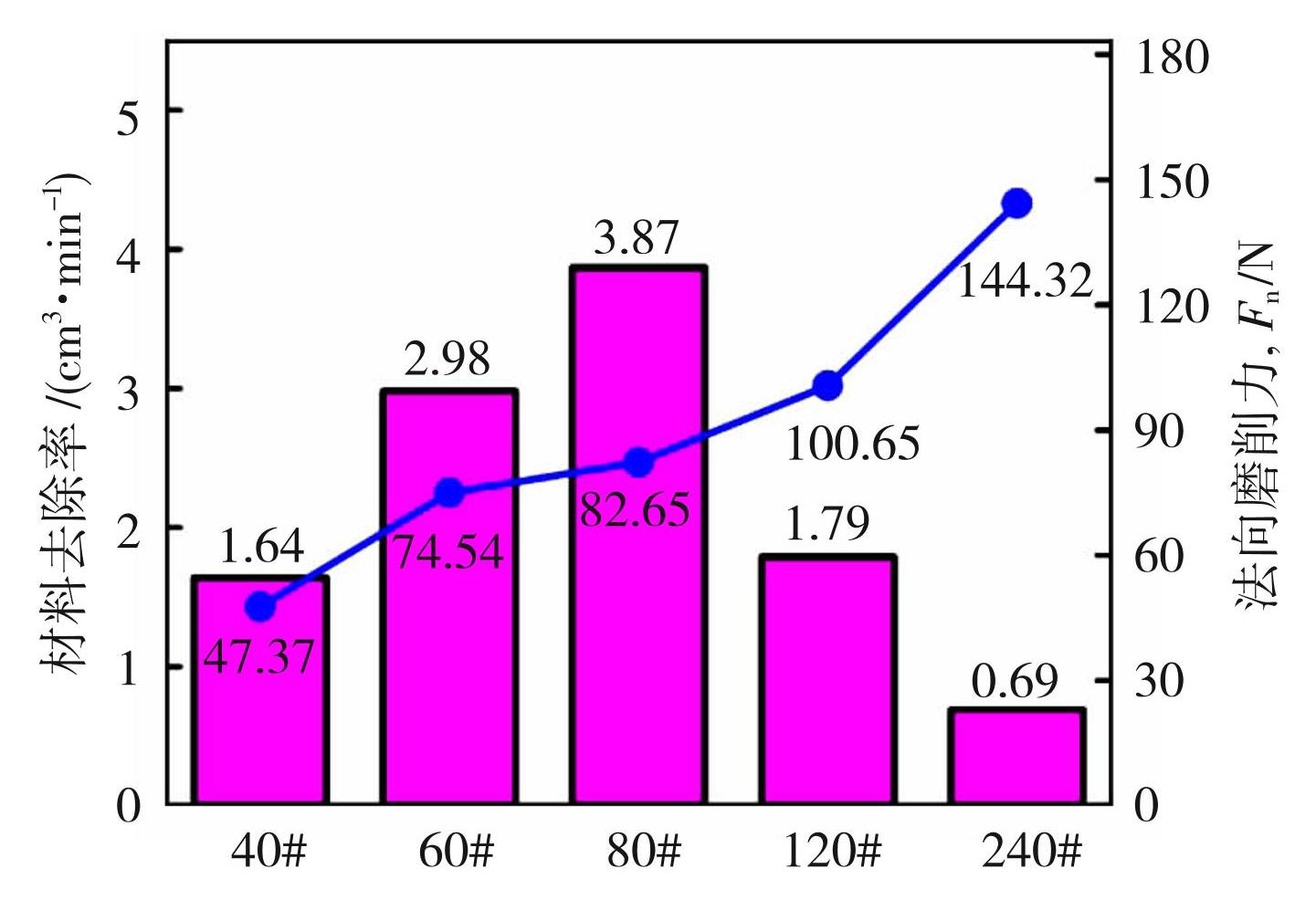
图6磨具目数对材料去除率的影响
Fig.6Effect of number of mills on material removal rate
1.3.2 单因素实验法
单因素实验法是分析各因素适宜取值范围的常用方法,选择对材料去除率影响较大的磨具转速、磨削速度和下压深度为约束条件,在法向磨削力合理的前提下以材料去除率为优化目标进行分析。
根据图7所示的单因素实验结果得到各因素的取值范围。磨具转速n、磨削速度Vw和下压深度Δh的取值范围分别为7 000~11 000 r/min、180~300 mm/min和3~5 mm。
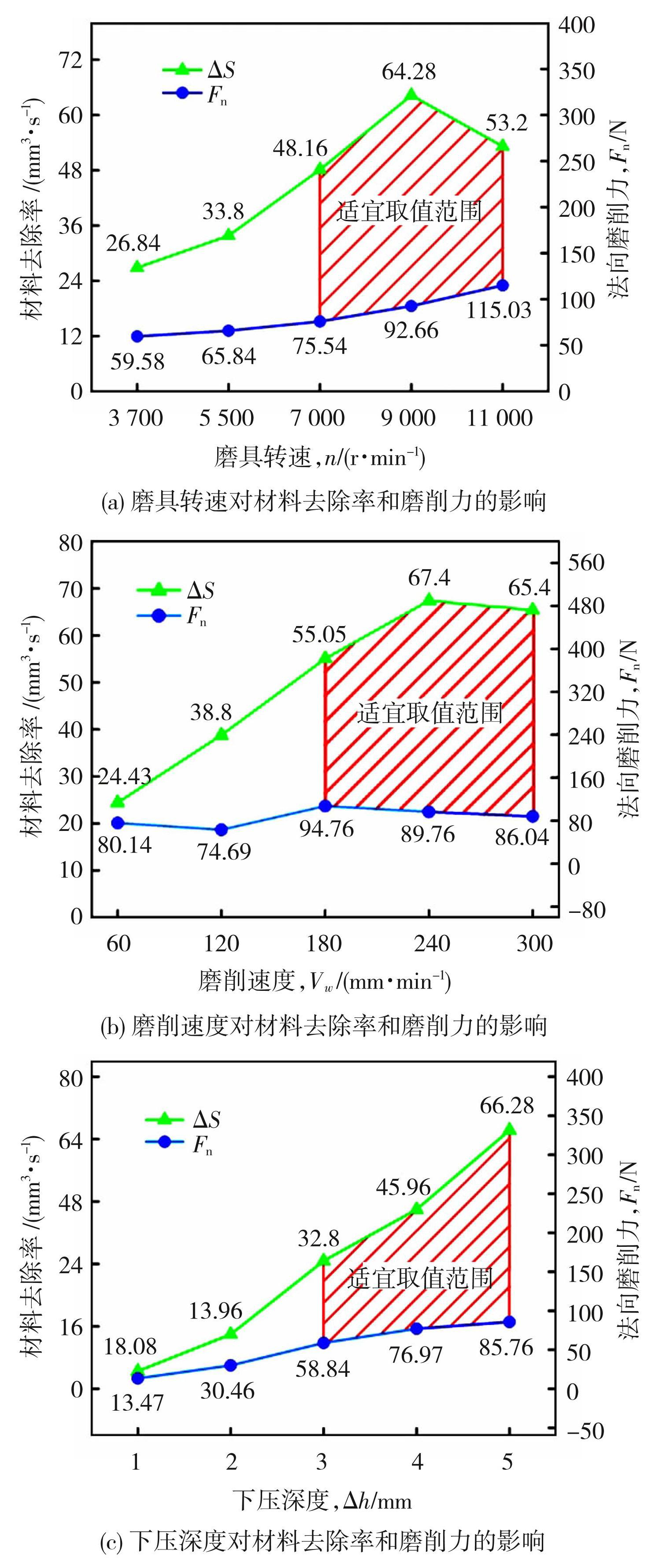
图7多因素适宜取值范围分析
Fig.7Analysis of appropriate value range of each factor: (a) effect of tool speed on material removal rate and grinding force; (b) effect of grinding speed on material removal rate and grinding force; (c) effect of pressure depth on material removal rate and grinding force
2 响应面预测模型
2.1 基于响应面法的实验设计
响应面法(Response Surface Method)作为一种优化设计方法而被广泛应用于各个领域[13],本文用Box-Behnken(BBD)方法设计实验并建立响应面模型,用二次回归方程的方法对变量与结果之间的函数关系进行拟合,具有序列性、正交性和旋转性质,适用于因素的非线性影响研究和大量组合实验分析,减少实验次数。为了研究磨削参数对材料去除率的影响,将磨具转速n、磨削速度Vw和下压深度Δh作为设计变量,设计变量取值如表1所示;实际应用时,用ΔS代替MRR使计算更简便,因此将材料去除面积ΔS及法向磨削力Fn作为响应变量,用响应面法得到设计变量对材料去除率的预测模型。
表1响应面设计变量取值
Table1Values of design variables in response surface design

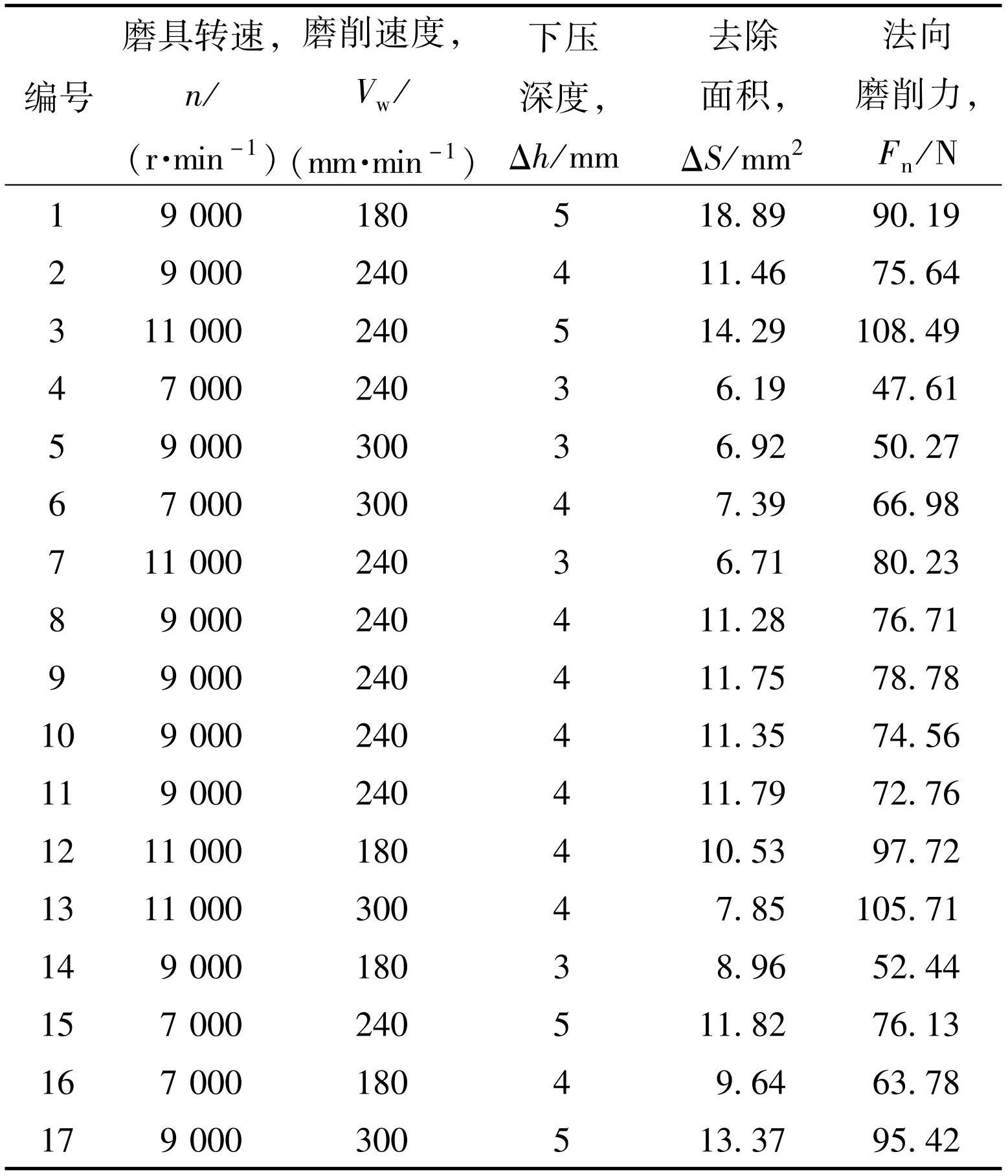
利用Design-Expert10软件的响应面模块在变量范围内进行BBD实验设计,根据响应面设计原理得到17组不同的设计变量组合,分别进行实验并统计不同参数下的材料去除面积和法向磨削力,结果如表2所示。
表2响应面法的实验方案及结果
Table2Test protocol and results of response surface method
2.2 响应面预测模型建立
根据表2所示的实验结果,将所得数据进行多元线性拟合和二次多项式拟合,建立材料去除面积ΔS及法向磨削力Fn与设计变量磨具转速n、磨削速度Vw和下压深度Δh之间的回归模型,材料去除面积的方差分析结果如表3、表4所示,法向磨削力的方差分析结果如表5、表6所示。
表3材料去除面积的方差分析结果
Table3ANOVA results of material removal area
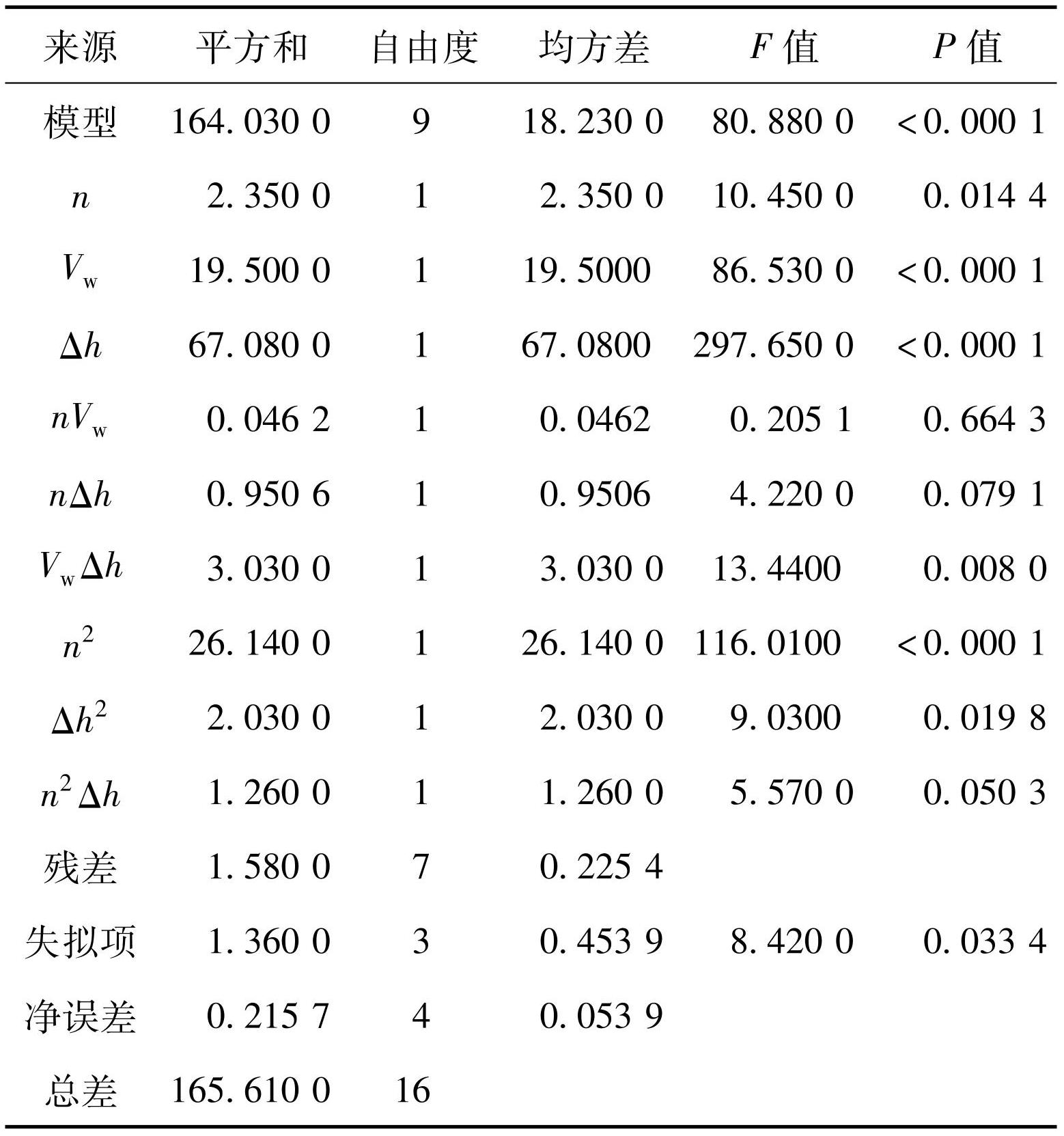
表4材料去除面积模型精度分析
Table4Material removal area model accuracy analysis

在表3和表4中,以相关系数R2作为模型的评判标准,失拟项P值体现了模型及各因素的显著性程度。由表3可知,材料去除面积响应面模型的R2为0.990 5、P值<0.000 1,证明此模型具有统计学意义[14];磨削速度Vw、下压深度Δh和n2对材料去除面积的影响极其显著(P<0.000 1),n、VwΔh、Δh2和n2Δh的P值均小于0.050 0,影响较为显著,其余项均不显著。材料去除面积ΔS的响应面模型为
(6)
由表5可知,法向磨削力响应面模型的R2为0.992 5、P值<0.000 1;磨具转速n和下压深度Δh对法向磨削力的影响及其显著,n2、Δh2和n2Δh对法向磨削力的影响较为显著,其余项均不显著。法向磨削力Fn的响应面模型为:
(7)
表5法向磨削力的方差分析结果
Table5ANOVA results of normal grinding force

表6法向磨削力模型精度分析
Table6Normal grinding forcemodel accuracy analysis

图8为响应面预测模型预测值与磨削实验实际值的对比。数据点分布越接近直线y=x,表明预测模型准确度越高,这说明式(6)和式(7)能够准确地预测材料去除面积及法向磨削力的值。
2.3 双因素交互分析
在分析磨削过程中各项参数对材料去除面积和法向磨削力的影响时,构建了三维曲面图以描述设计变量与响应变量的关系,图形曲面的陡峭程度反映了参数对结果的影响程度。图9为设计变量与材料去除面积的三维响应面图,分析图9可知,下压深度对材料去除面积影响最大,随着下压深度的增大,材料去除面积的增大趋势由缓到急;角磨机转速对材料去除面积的影响其次,随着角磨机转速的增大,材料去除面积先增大后减小,最优转速为9 000 r/min;磨削速度对材料去除面积的影响较小,随着磨削速度的增加,材料去除面积缓慢减小。
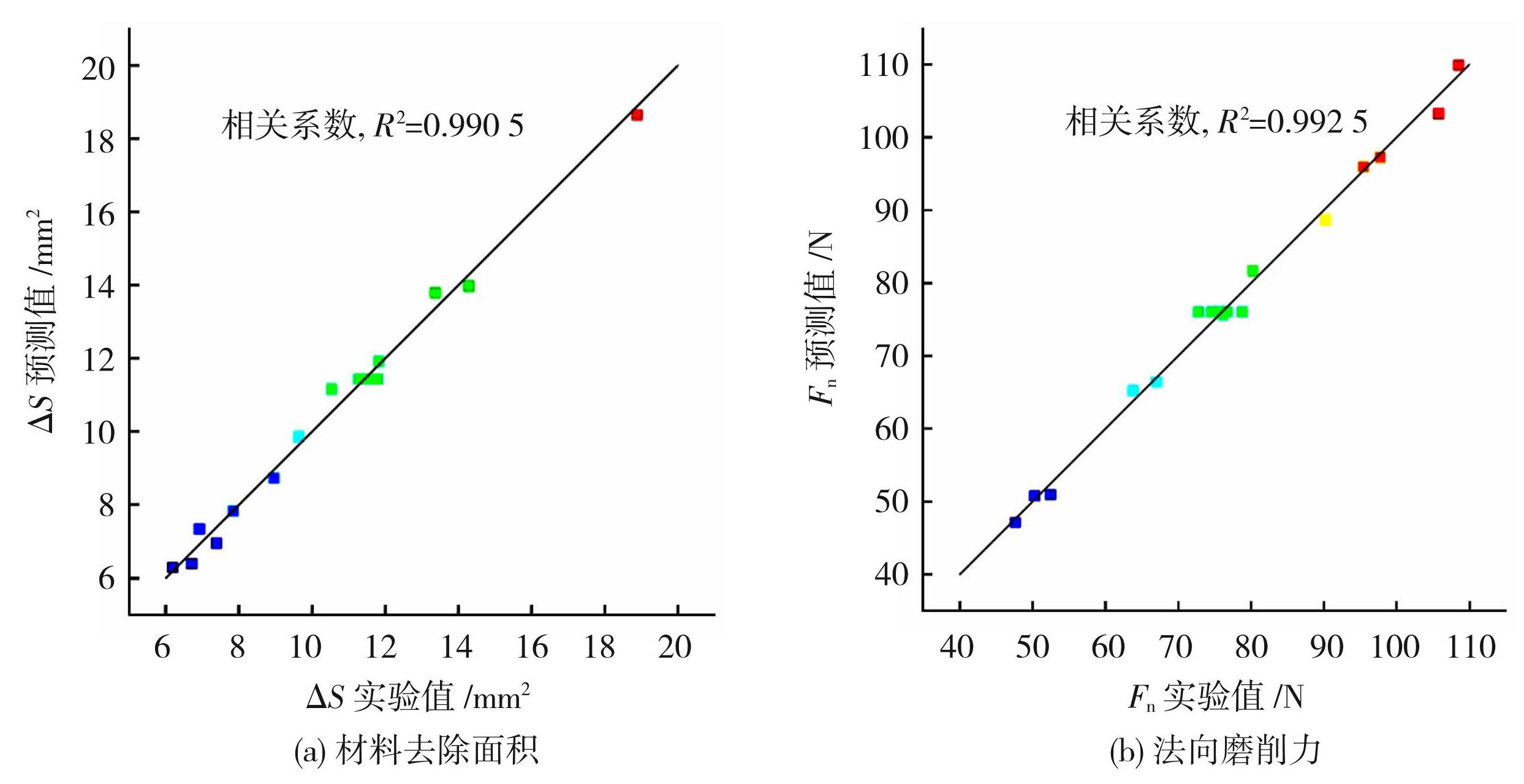
图8模型预测值与实验样本值对比
Fig.8Comparison between predicted model values andexperimental sample values: (a) area of material removal; (b) normal grinding force
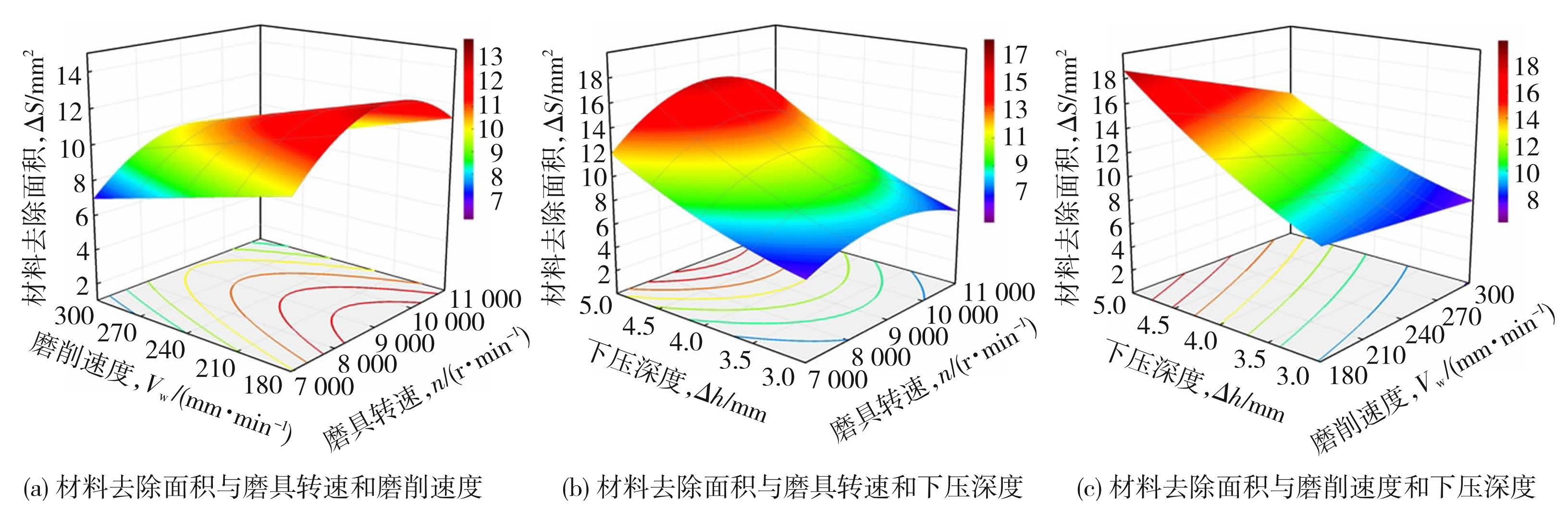
图9材料去除面积响应面图
Fig.9Material removal area response surface map: (a) material removal area and abrasive speed and grinding speed; (b) material removal area and abrasive speed and pressure depth; (c) material removal area and grinding speed and depth of pressing
图10为实验参数对法向磨削力的响应面图,图10(a)可以看出,法向磨削力受磨具转速影响较大,转速较小时,法向磨削力随着转速的增大缓慢增大,当转速超过9 000 r/min后,法向磨削力开始显著增大;磨削速度对法向磨削力的影响很小。分析图10(b)可知,下压程度和磨具转速对法向磨削力的影响程度接近,法向磨削力随下压深度的增加而增大。
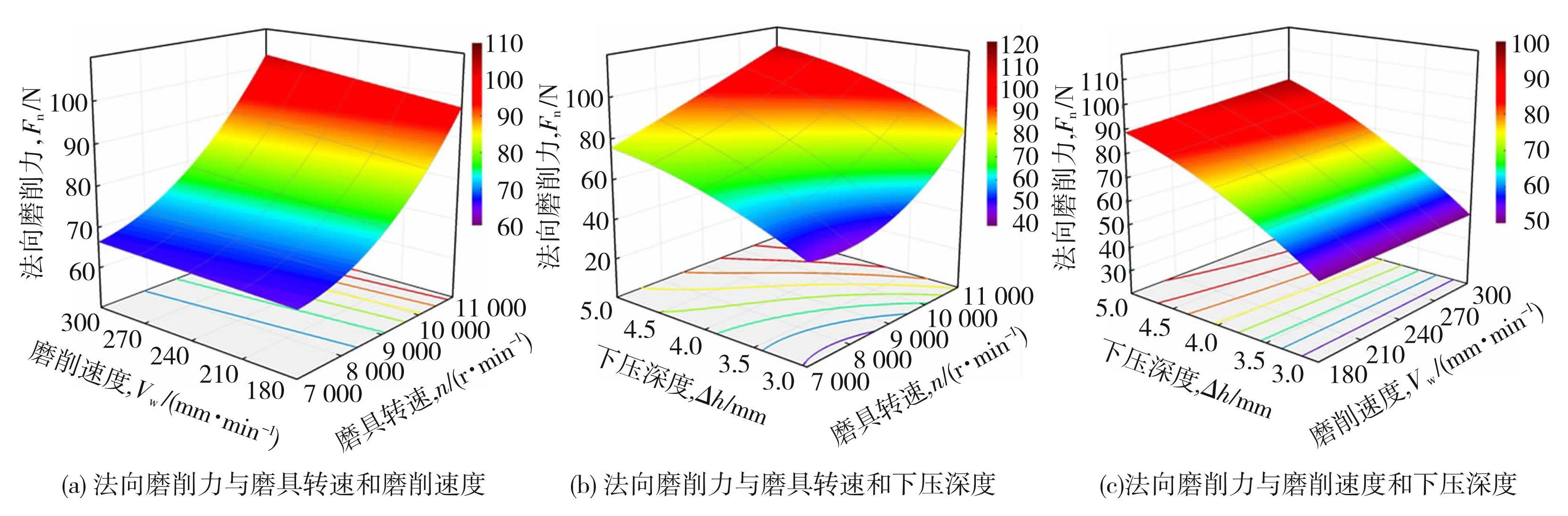
图10法向磨削力响应面图
Fig.10Normal grinding force response surface diagram: (a) normal grinding force and grinding speed and grinding speed; (b) normal grinding force and grinding tool speed and pressure depth; (c) normal grinding force with grinding speed and depth of downward pressure
上述分析可知,各设计变量对材料去除面积和法向磨削力的影响各有不同。实际磨削过程中,需优先保证材料去除面积为最大,即ΔSmax=18.67 mm2;其次保证法向磨削力较小,对应的设计变量为下压深度5 mm、角磨机转速为9 000 r/min、磨削速度180 mm/min。但是,为了保证效率,仍应选择较大的磨削速度。最优设计变量选择下压深度为5 mm、角磨机转速为9 000 r/min、磨削速度为300 mm/min,对应的材料去除面积为ΔSc=13.8 mm2。
2.4 响应面模型预测与验证
如表7和表8所示,为了验证预测模型的有效性,选择设计变量取值范围内的参数对材料去除面积和法向磨削力分别进行5组实验,将实验值与预测值对比。
表7材料去除面积的响应面预测值与实验结果对比
Table7Comparison between predicted response surface values and experimental results of material removal area
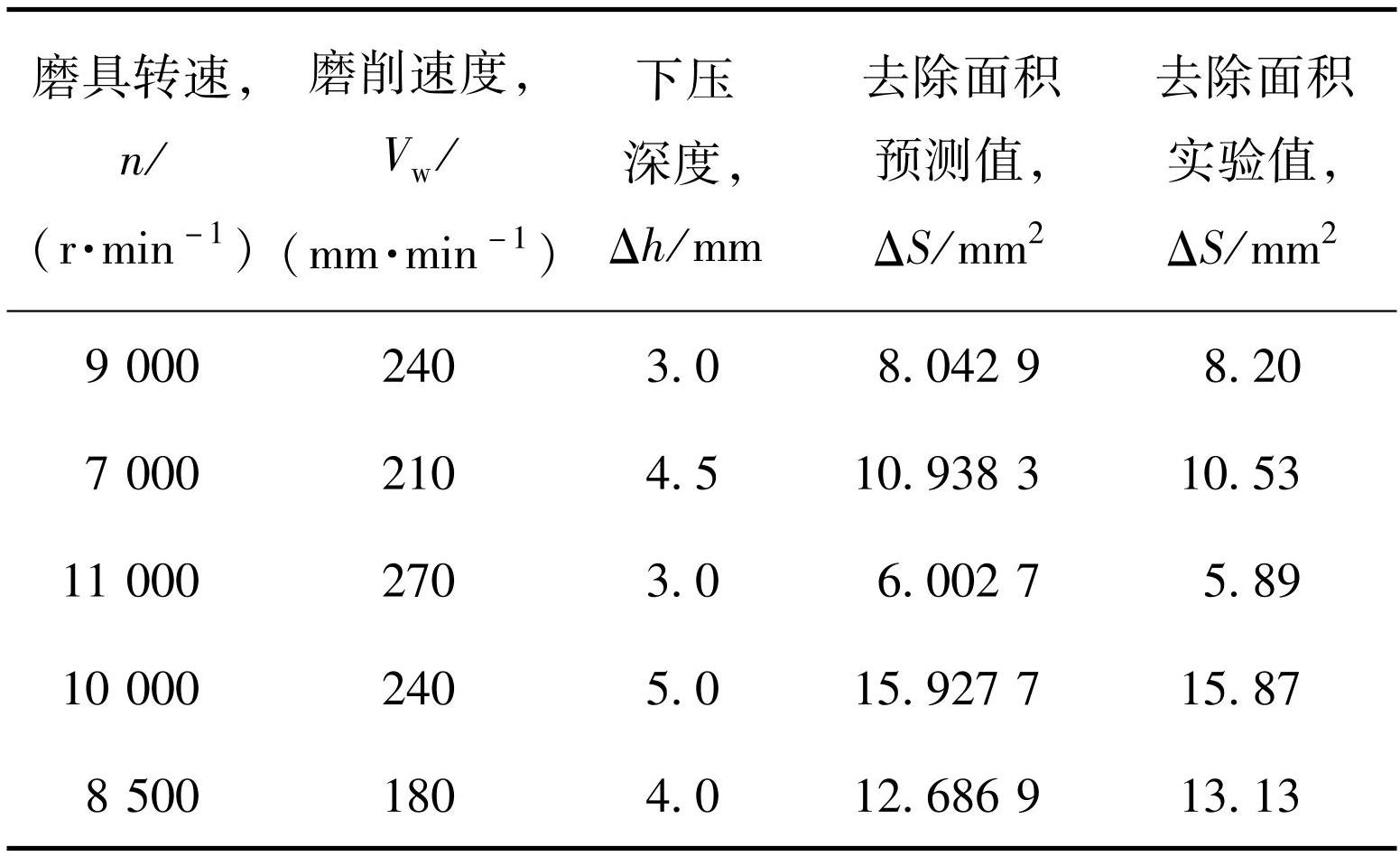
表8法向磨削力的响应面预测值与实验结果对比
Table8Comparison between predicted response surface values and experimental results of normal grinding force
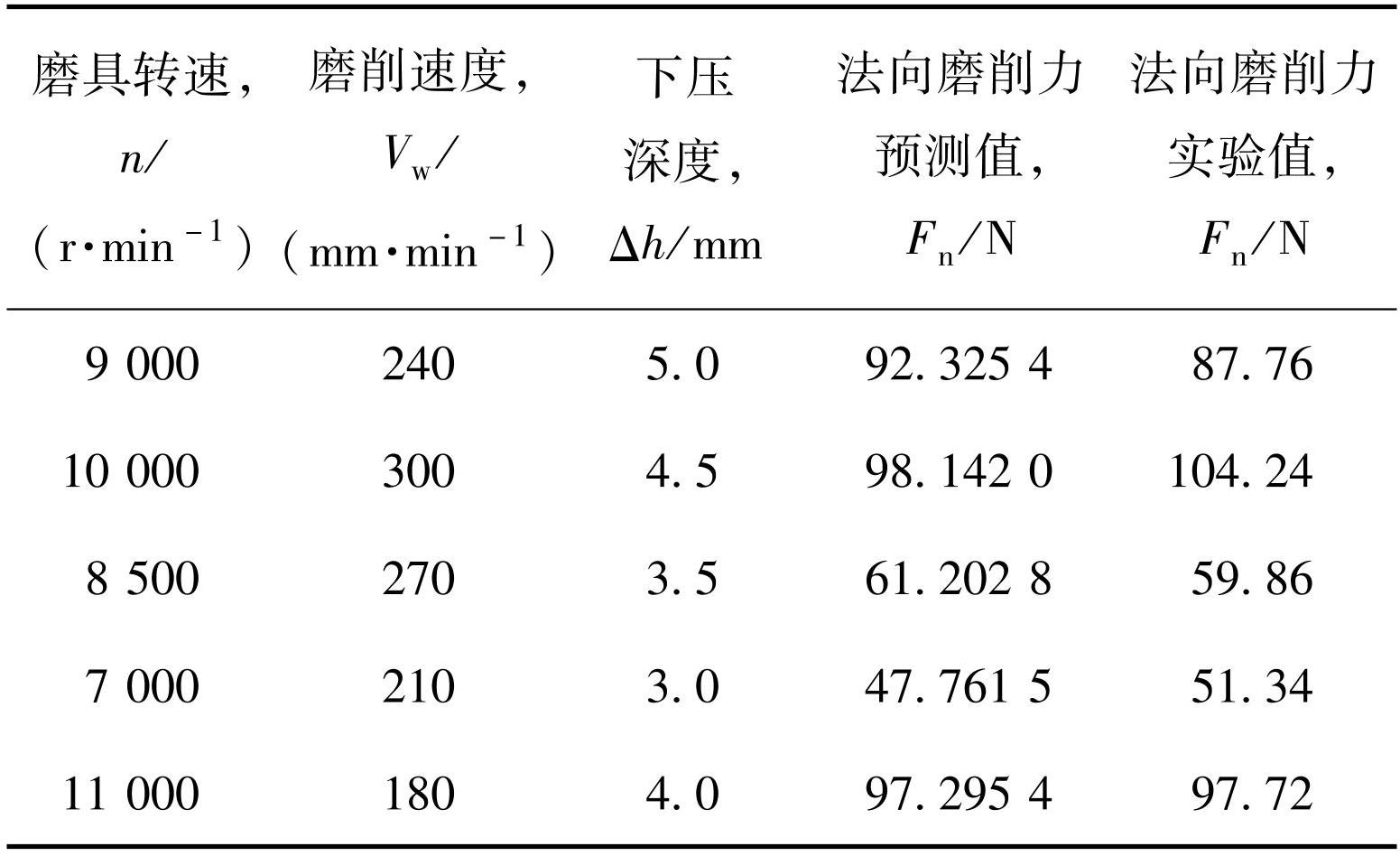
对比结果可以看出,材料去除面积响应面预测模型的预测值与实验值吻合较好,最大误差为3.8%;法向磨削力的预测值与实验值误差较大,但误差均在7%以内。
3 焊缝余高打磨自适应补偿策略
焊接成型的石油管道经常会出现局部焊缝余高过高的问题,其焊缝在不同位置的宽度、高度各不相同。针对这种具有复杂几何特征的管道环焊缝,单一的磨削工艺往往不能达到预期的磨削效果,打磨过深时打磨头易对母材造成损害,打磨过浅时则达不到预期打磨效果。因此,以预测模型为基础提出了焊缝余高打磨自适应补偿策略。
3.1 焊缝分层方法
对于具有复杂几何特征的环焊缝,学者们通常预先使用线激光传感器对其表面形貌进行三维建模,并从焊缝形貌中提取不同截面的宽度和余高等特征[15]。利用将焊缝表面轮廓简化为抛物线建立的数学模型,可对截面中所需去除的材料面积进行求解。
石油管道对于管体的强度有很高的要求,因此经常会要求打磨头与基材保持1~2 mm安全距离。然而,对于部分截面过大的焊缝,仍无法通过单次打磨就达到预期效果。因此,如图11所示,将焊缝截面需打磨的面积拆分为ΔS1、ΔS2···ΔSn。为保证效率,打磨ΔS1···ΔSn-1时使用最优工艺参数,即ΔS1=ΔS2=···=ΔSn-1=ΔSc。经n-1次磨削后,若剩余需打磨面积小于ΔSmax,剩余面积为ΔSn,如式(8)所示
(8)
根据焊缝表面数学模型,可对每次打磨后的余高h1、h2、···、hn进行求解,余高的值满足式(9)
(9)
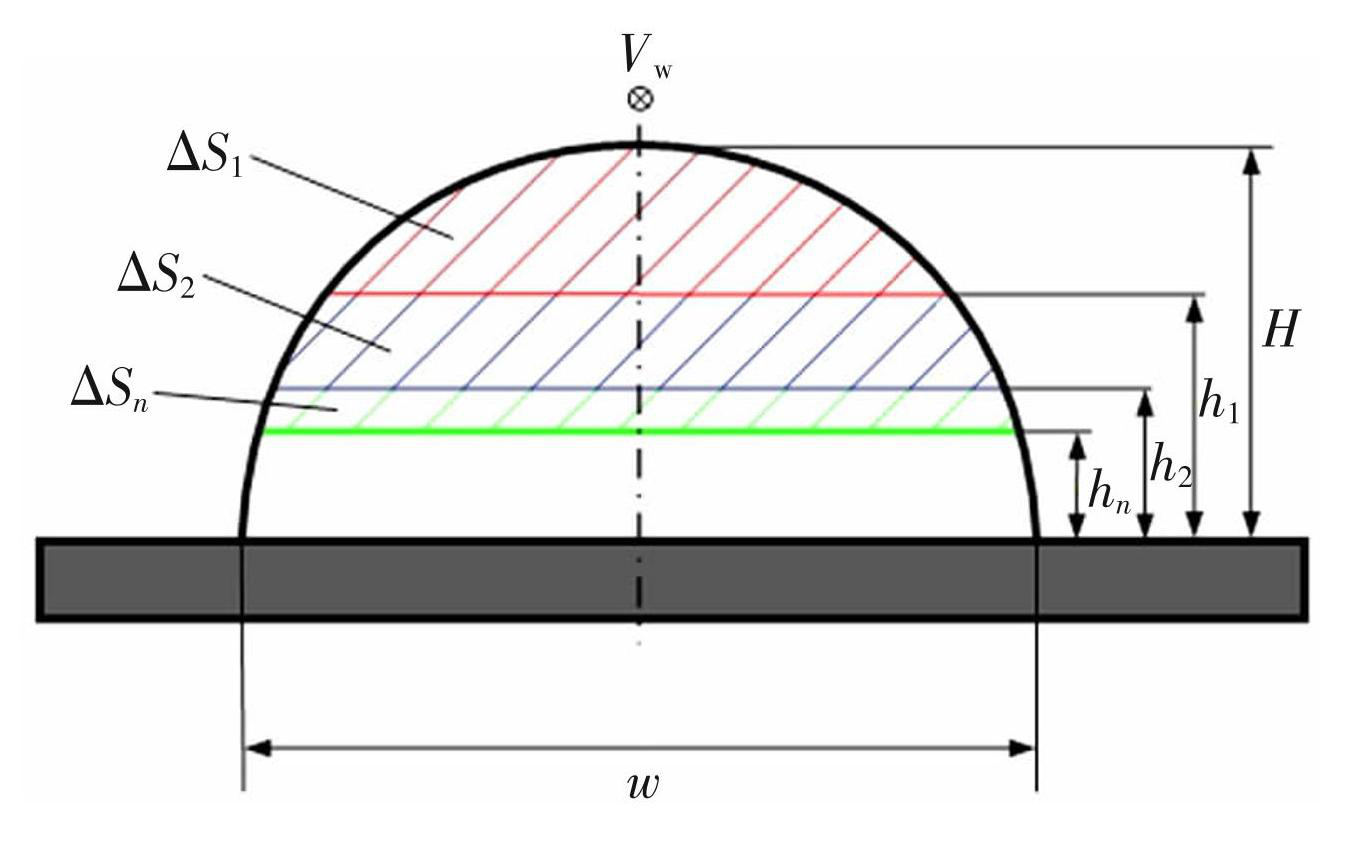
图11焊缝单截面分层
Fig.11Weld seam single section layering
3.2 分层工艺预测
焊缝分层后,需对每一层的工艺参数进行规划。由于随着磨具转速的提高,材料去除面积先增大后减小,因此,在工艺规划时将转速n设定为固定值9 000 r/min。其中,ΔS1、ΔS2···ΔSn-1对应的工艺参数为上文中得到的最优工艺参数。
ΔSn对应的工艺参数则使用预测模型求解。基于响应面预测模型可知,Vw=300 mm/min时,ΔS最大可达13.8 mm2;当速度为Vw=240 mm/min时,ΔS最大可达16.23 mm2;当速度Vw=180 mm/min时,ΔS最大可达18.67 mm2。在实际加工中,应使磨削速度尽量加快来提高磨削效率,因此,磨削速度的规划应以式(10)为判断依据。
(10)
确定n与Vw后,基于响应面预测模型(式(6))求解下压深度的值。
3.3 自适应补偿策略工艺规划软件
针对截面相对一致的焊缝,磨削工艺可不随位置变化。定义焊缝宽度、焊缝余高以及与母材的安全距离,即可得出磨削次数及磨削工艺,计算流程如图12所示。
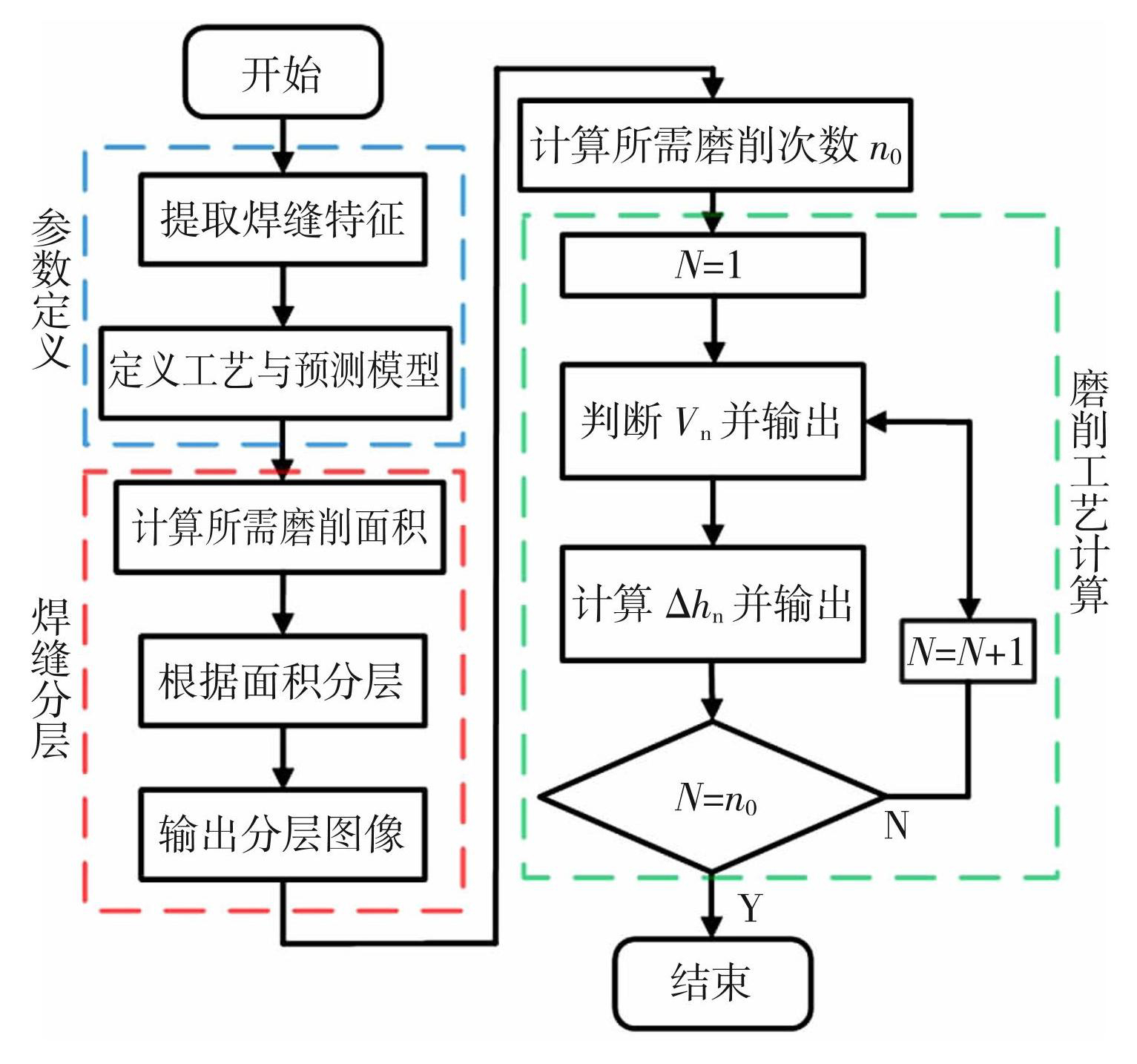
图12单截面焊缝磨削参数规划流程图
Fig.12Flow chart of single section weld grinding parameters
针对截面特征变化较大的焊缝,磨削工艺需要随位置变化。焊缝经三维轮廓扫描仪扫描后,可从表格文件中提取焊缝截面数据,根据多个截面宽度、余高对焊缝进行三维建模,并通过预处理得到截面数量和截面间隔。3参数计算流程如图13所示,首先对工艺规划及预测模型进行输入,也可选择使用预置的预测模型,对多个截面分别进行分层及工艺计算。计算后,输出焊缝分层图像及打磨头的磨削路径,如图14所示,图中蓝色线条为第一次打磨路径,橙色和黄色分别为第二次、第三次打磨路径。最后将磨削参数导出至表格文件。
3.4 磨削策略实验验证
为了验证上述分层策略和工艺规划方法的有效性,处理得到不平整的焊缝,如图15所示。

图13多截面焊缝磨削参数规划流程图
Fig.13Flow chart of multi-section weld grinding parameter
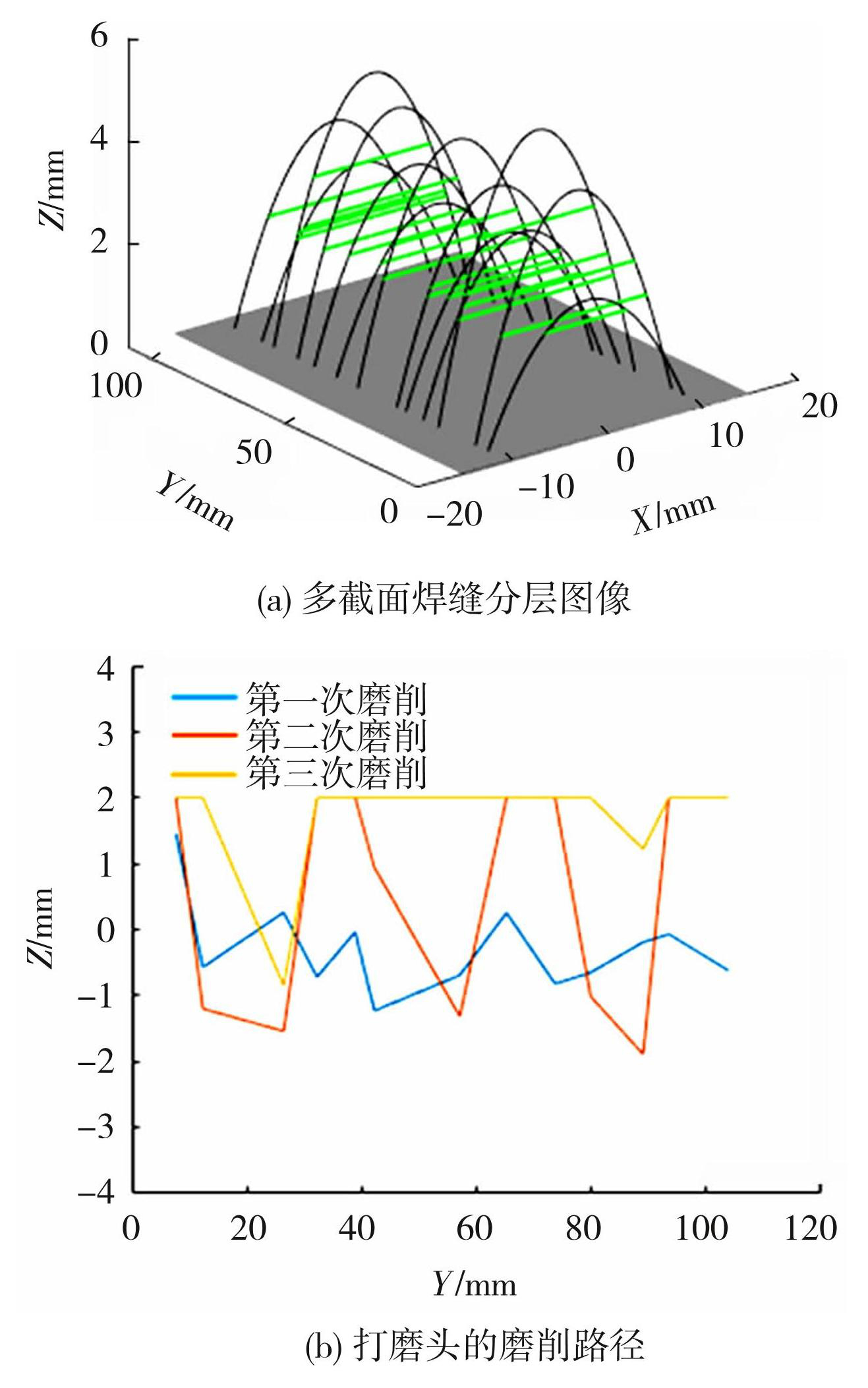
图14多截面焊缝分层及磨削路径规划
Fig.14Multi-section weld delamination and grinding path planning: (a) multi-section weld layered image; (b) grinding path of abrasive
对焊缝在不同位置的宽度、高度进行测量。提取焊缝宽度、高度,使用自适应补偿策略工艺规划软件输出不规则焊缝的磨削工艺,并与一般方法对比,实验结果如图16所示。可见,一般方法无法对不同的焊缝高度进行调整,磨削得到的结果与预期值相差较大,自适应补偿策略在焊缝不同位置对参数实时调整,打磨后焊缝余高与预期值最大误差为0.32 mm。
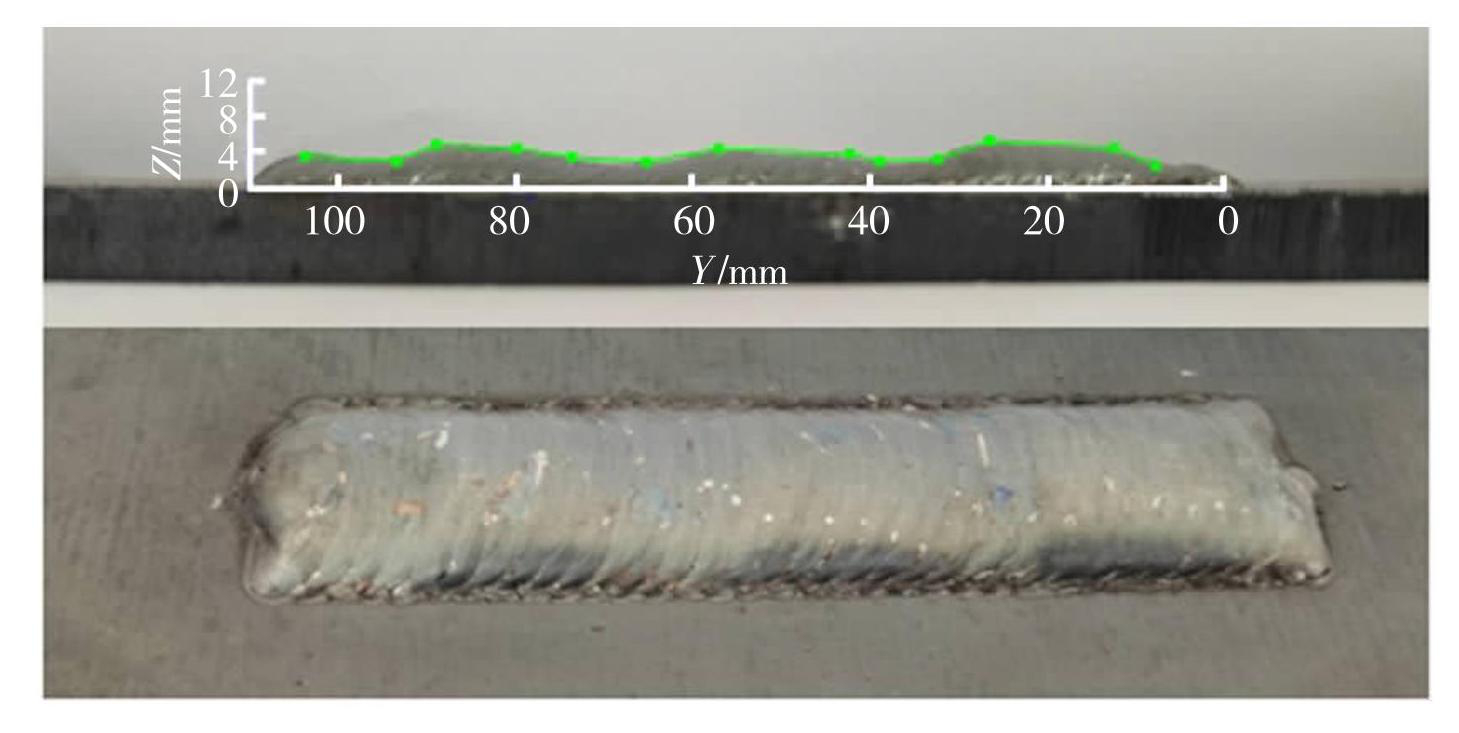
图15不规则焊缝
Fig.15Irregular welds
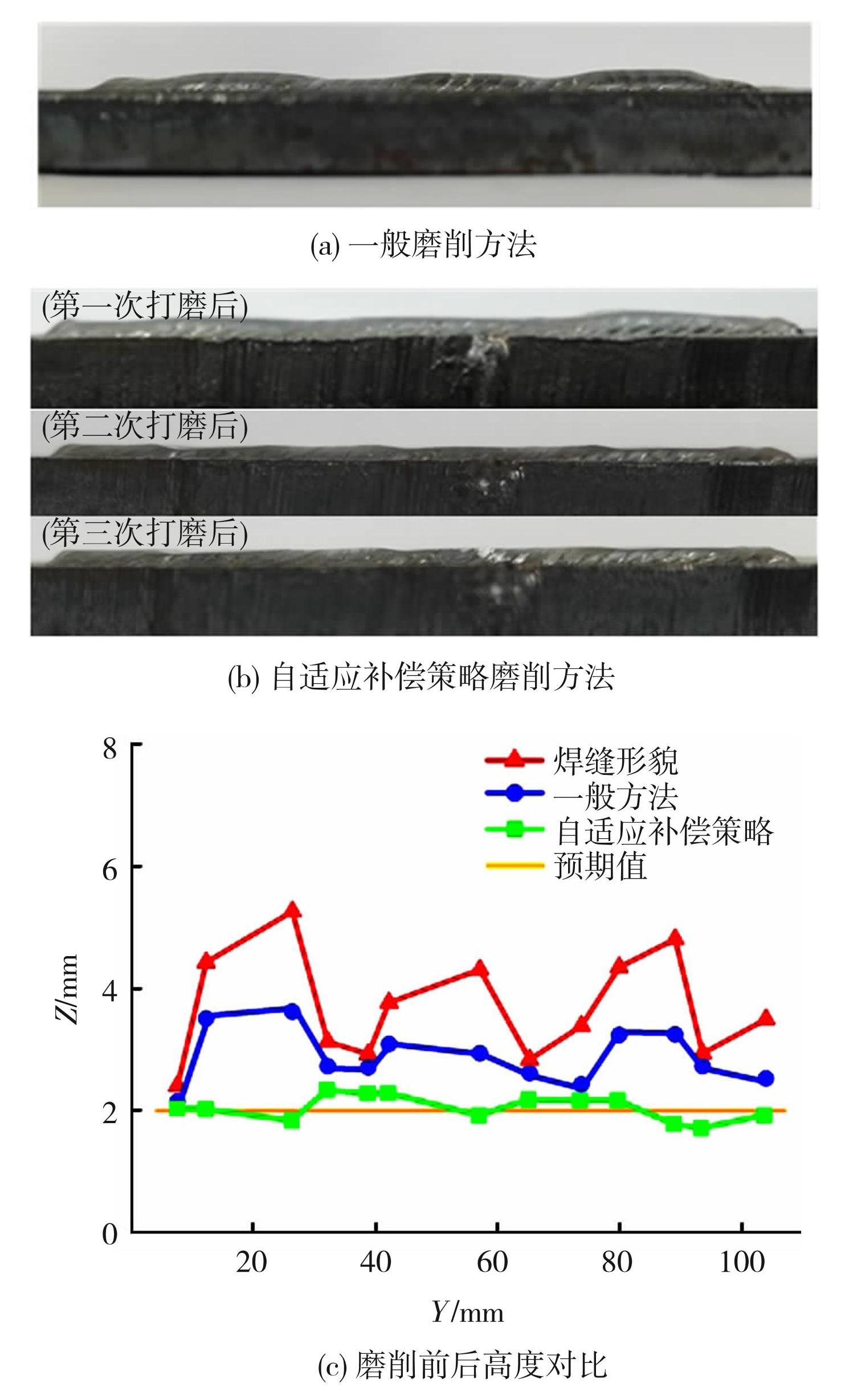
图16自适应补偿策略磨削方法与一般方法
Fig.16Adaptive compensation strategy approach vs. general approach: (a) general grinding method; (b) adaptive compensation strategy grinding method; (c) comparison of height before and after grinding
4 结论
1)建立了焊缝表面轮廓的数学模型,提出了考虑磨具自身柔性变形的、基于材料去除面积的焊缝余高打磨自适应补偿策略。
2)确定了磨削工艺的适宜取值范围为磨具转速7 000~11 000 r/min、磨削速度180~300 mm/min和下压深度3~5 mm;得到了最优工艺参数,即下压深度为5 mm、角磨机转速为9 000 r/min、磨削速度为300 mm/min。ΔS和Fn预测值与试验值的最大误差分别为3.9%和6.8%。
3)建立了余高打磨分层策略的数学模型及不同层的工艺规划方法,建立了具有模型读取、等材料去除面积分层、预测模型设置、工艺规划、数据导出等功能的程序算法。
4)对提出的余高打磨策略进行验证,实验表明,打磨后的焊缝余高与预期值的最大误差为0.32 mm。
