摘要
针对机械除鳞工艺中因氧化皮结构复杂,其破裂机理及力学性能难以掌握、除鳞工艺参数难以精确设定的问题,本文采用分子动力学模拟方法,建立多晶FeO/Fe模型,设置裂纹缺陷,模拟单轴拉伸下应变率和裂纹位置对多晶FeO/Fe断裂变形的影响。研究表明:从中心对称参数可得原子紊乱程度不同,其由高到低的区域依次为裂纹缺陷>原始晶界>原始FeO/Fe界面>原始多晶内部;当应变率一定时,多晶FeO/Fe断裂行为有差异,完美模型(即无缺陷)及裂纹位于晶内、晶界时,失效方式为沿晶断裂;裂纹位于FeO/Fe界面时,失效方式为界面断裂。裂纹位于相同位置时,随着应变率从1×109 s-1增大到1×1010 s-1,位错总数量从51条增至105条,总长度从58.78 nm增至112.11 nm,模型塑性变形更强,抗拉强度逐渐升高,由2.21 GPa增大到3.25 GPa,且裂纹断裂程度逐渐减小。研究结果可对掌握氧化皮的破裂机理提供理论帮助,为精确除鳞工艺参数提供指导。
Abstract
To address the challenges in understanding the complex fracture mechanisms and mechanical properties of scale layers in mechanical descaling processes, as well as the difficulty in accurately setting descaling process parameters, this study utilizes molecular dynamics simulation methods to establish a polycrystalline FeO/Fe model with crack defects. The effects of strain rate and crack location on fracture deformation of polycrystalline FeO/Fe under uniaxial tensile were simulated. The research reveals that based on the central symmetry parameter, the degree of atomic disorder varies, with regions in descending order of disorder being the crack defect>original grain boundary>original FeO/Fe interface>original polycrystalline interior. When the strain rate is constant, different fracture behavior are observed in polycrystalline FeO/Fe. In the perfect model (without defects), the crack is located inside the grain or at grain boundaries, the failure mode is transgranular fracture.However, when the crack is located at the FeO/Fe interface, the failure mode shifts into interfacial fracture. For cracks located at the same position, as the strain rate increases from 1×109 s-1 to 1×1010 s-1, the total number of dislocations increases from 51 to 105, and the total length increases from 58.78 nm to 112.11 nm, indicating a higher plastic deformation in the model.Consequently, the tensile strength gradually increases from 2.21 GPa to 3.25 GPa while the extent of crack fracture diminishes. The research results of this paper can provide theoretical assistancein understanding the rupture mechanisms of oxide and offer guidance for accurately descaling process parameters.
Keywords
在热轧过程中,金属表面会形成一层致密的氧化皮[1-3],其存在会影响板带后序的冷轧、镀锌加工的表面质量,因此需要将其去除。目前,磨料水射流机械除鳞是无酸除鳞方式的研究热点之一。但受限于氧化皮内部存在裂纹等缺陷,在机械外载荷作用下,研究者对于其破裂失效机理尚未完全了解,导致无法为机械除鳞工艺参数提供数据支撑,因此,迫切需要对氧化皮的破裂失效过程及力学性能进行深入研究。
材料的失效过程及力学性能受应变率影响而变化。刘颖等[4]研究了DZ2车轴钢在不同应变率下的拉伸失效和力学性能,发现位错滑移和韧性断裂是DZ2车轴钢塑性变形和失效的主要机制,其抗拉强度随着应变率不同存在较大差异,当应变率高于10 s-1时,其变形抗力和强度随应变率增加而增大,应变率低于10 s-1时,位错密度低,其强度具有低的应变率敏感性,不随应变率变化而显著变化。陈跃良等[5]研究了38CrMoAl钢在高应变率下动态失效力学行为,发现随着应变率的升高,材料屈服强度上升,塑性同时降低。Zhang等[6]研究了CMSX-4合金不同应变率下拉伸失效机理,结果发现在低应变率下合金为跨晶断裂,屈服应力及强度较低,高应变率下导致更高的屈服应力和更高强度,可以观察到具有明显裂面的平裂,断裂形态特征与裂解和跨晶混合。传统实验方法难以观察到材料内部微观结构的演变过程。分子动力学(Molecular Dynamics,简称MD)[7-8]模拟可准确记录原子或组织结构在飞秒、皮秒下的变化,已被证实其是研究材料在不同应变率下变形行为的最有效手段[9-12]。李源才等[13]研究了不同应变率对单晶/多晶镍拉伸断裂的影响,研究发现,随着应变率的升高,SPS Ni中fcc原子逐渐变为非晶原子,失效机制主要由位错孪晶和原子大规模的非晶化造成。成聪等[14]研究了不同应变率下多晶Cu/Ni薄膜的变形行为,结果表明,随应变率的增加,裂缝数量增加,Cu薄膜呈碎裂形式被破坏。
对于带钢表面氧化皮与基体组成的膜/基系统,其内部及界面通常存在微裂纹等缺陷,在外载荷作用下,氧化皮及界面的失效受到上述缺陷影响。宏观尺度上的动态损伤与断裂理论模型[15],没有考虑孔洞、裂纹等缺陷,在MD软件中可以设置。周瑾等[16-17]通过设置孔洞,研究了孔洞数量及孔洞尺寸对单晶FeO/Fe界面处裂纹扩展的影响;樊铭洋等[18]在FeO晶内设置孔洞缺陷,研究了孔洞尺寸对单晶FeO/Fe断裂失效的影响;常筠袖等[19]在单晶TiAl涂层中设置孔洞和裂纹,研究孔洞对裂纹扩展的影响;任鹏飞[20]在单晶硅中设置裂纹缺陷研究位错与裂纹相互作用的影响。但上述研究大多针对于单晶体系,对氧化皮中多晶体系的裂纹扩展研究相对较少。而多晶FeO/Fe的裂纹扩展和断裂失效与裂纹所处位置密切相关,除了FeO晶内,还包括晶界和界面。因此本文以多晶FeO/Fe作为研究对象,采用MD模拟方法对其失效过程进行研究,在纳观尺度上基于位错理论探究单轴拉伸下裂纹位置和应变率对多晶FeO/Fe模型断裂变形及力学性能的影响,以进一步掌握氧化皮破裂机理。
1 模拟条件与设置
本文采用分子动力学方法[21]和开源软件Atomsk结合Shell脚本的Voronoi方法,建立多晶FeO、Fe以及通过“merge”命令所建立FeO/Fe的初始模型如图1所示,其中,多晶Fe为体心立方晶体结构(bcc),晶格常数为0.288 6 nm,多晶FeO为面心立方晶体结构(fcc),晶格常数为0.433 2 nm,不同颜色代表不同晶粒。本模拟选择多晶FeO/Fe模型的尺寸约为10 nm×20 nm×10 nm,原子总数为183 961。Fe—O原子之间的作用力采用Tersoff[22]作用势,该作用势描述了α-Fe氧间隙原子的能量学和几何构型,符合密度泛函理论。其原子能量E计算方法如下
式中:rij为原子间距;VR和VA分别是排斥和吸引配对功能; fc为相互作用范围。VR和VA由二聚键能和长度以及控制相对电势形状的拟合参数计算所得。 fc受到截止参数的限制。
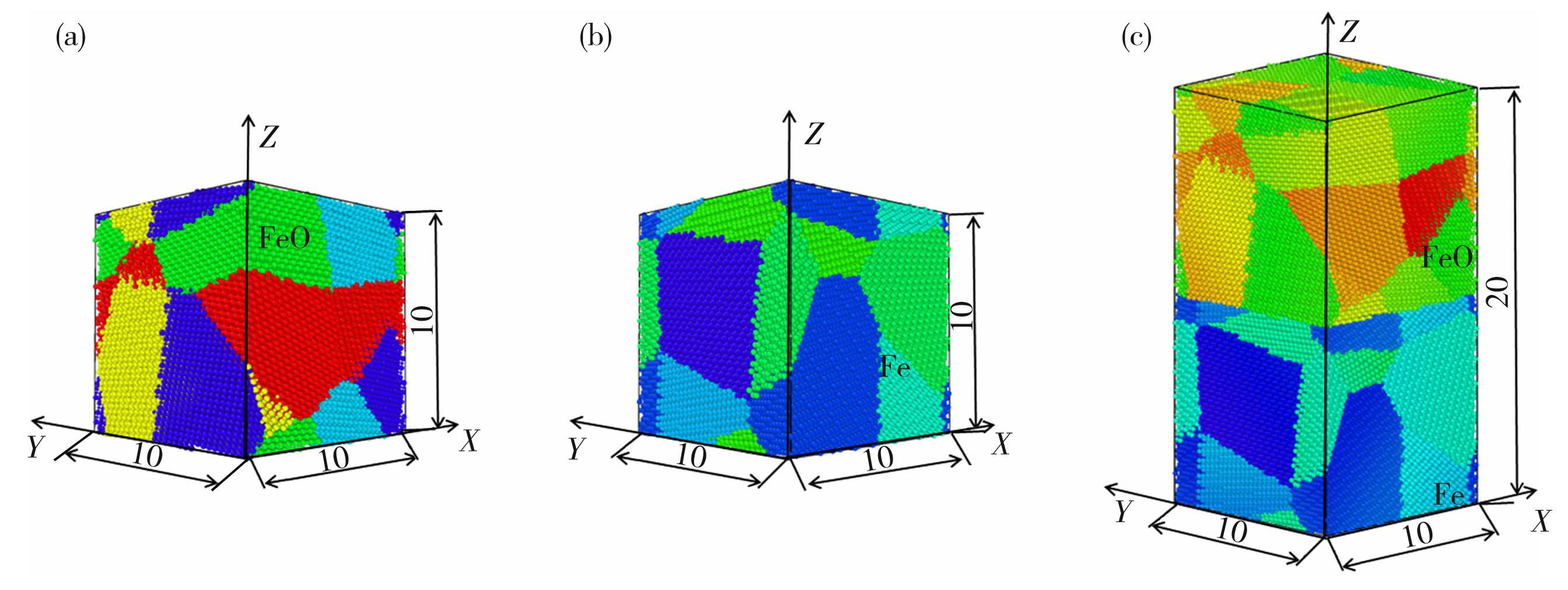
图1多晶FeO(a)、多晶Fe(b)、及多晶FeO/Fe模型示意图(c)(单位:nm)
Fig.1Polycrystalline FeO (a) , polycrystalline Fe (b) , and polycrystalline FeO/Fe models
在多晶FeO/Fe模型中,晶内、晶界、FeO/Fe界面等处通过删除原子的方法预制了一条裂纹面为(100)的裂纹,裂纹尺寸为3 nm×2 nm×1 nm,共584个原子,多晶FeO/Fe模型弛豫后裂纹位于不同位置中心对称参数(Center-Symmetry Parameter,CSP)示意图见图2,CSP数值表示原子晶格的紊乱程度,即CSP值越小晶格排列越有序,值越大晶格排列越紊乱。
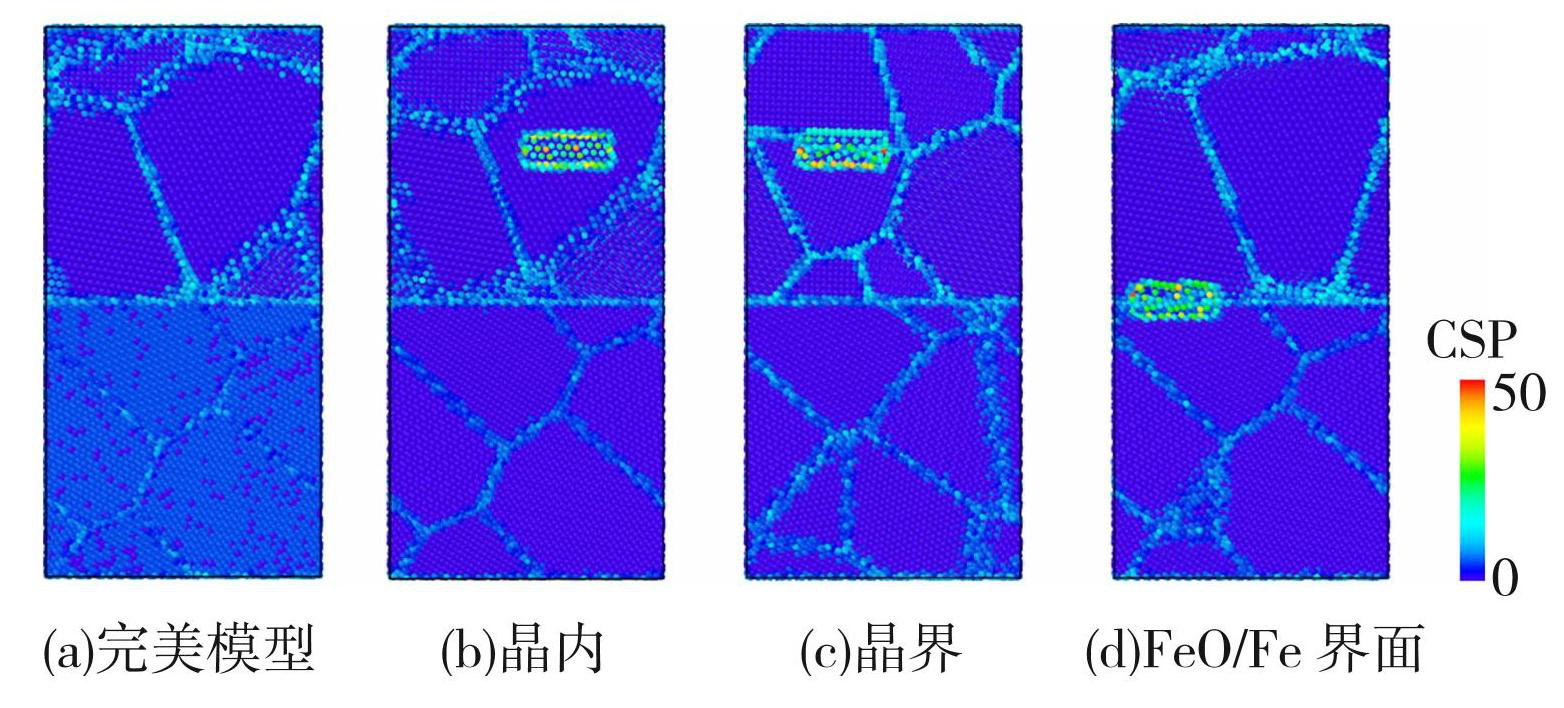
图2裂纹位于不同位置CSP示意图
Fig.2CSP diagram of cracks at different locations: (a) perfect model; (b) intracrystalline; (c) grain boundary; (d) FeO/Fe interface
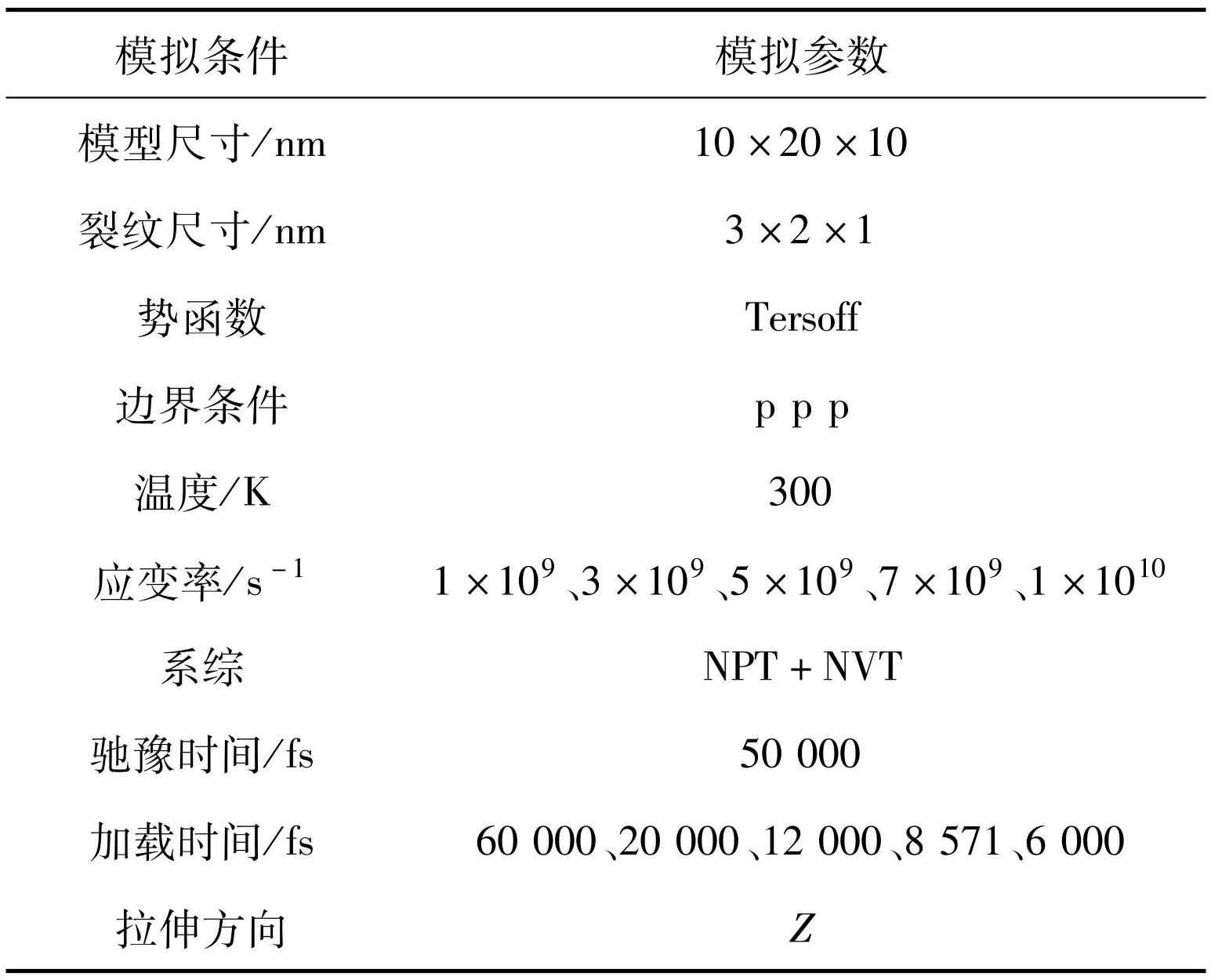
在模拟单轴拉伸过程中,首先在NPT系综下驰豫50 000 fs,步长为0.001 ps,使整个体系在加载之前达到平衡状态。弛豫中X、Y、Z的3个方向均设置为周期性边界,由于磨料射流除鳞过程中,颗粒冲击下攻击表面应变率为104~1010 s-1,因此,弛豫后在300 K下,分别以1×109、3×109、5×109、7×109、1×1010 s-1的高应变率沿Z方向进行拉伸加载,模拟Y-Z平面裂纹扩展的过程,直到临界应变达到0.04~0.05为止。模型参数设置见表1,模拟结果采用可视化软件OVITO(Open Visualization Tool)进行处理,通过CSP、应力应变关系、能量变化、抗拉强度等角度进行分析。
表1多晶FeO/Fe模拟条件设置的具体参数
Table1Specific parameters for simulation settings of polycrystalline FeO/Fe
2 结果与分析
2.1 裂纹位置对多晶FeO/Fe拉伸力学性能的影响
应变率为1×109 s-1时,裂纹位于不同位置时的应力-应变曲线图见图3(a)。从图3(a)可看出,裂纹位于不同位置的模型应力-应变曲线变化趋势基本相同,初始阶段的曲线上升基本一致,由此说明,在弹性阶段,裂纹缺陷对模型的应力作用不显著;当裂纹位于不同位置时,模型断裂时刻的临界应变均几乎接近0.03,完美模型(即无缺陷),裂纹位于晶内、晶界、FeO/Fe界面的4个模型的应力继续上升,逐渐达到最大值,分别为2.32、2.41、2.27、2.21 GPa,裂纹位于晶内的模型应力峰值最高,裂纹位于FeO/Fe界面时模型应力峰值最低。裂纹位于FeO/Fe界面和晶界相比位于晶内和完美模型优先断裂,说明晶界和FeO/Fe界面的裂纹降低了模型的抗拉强度。
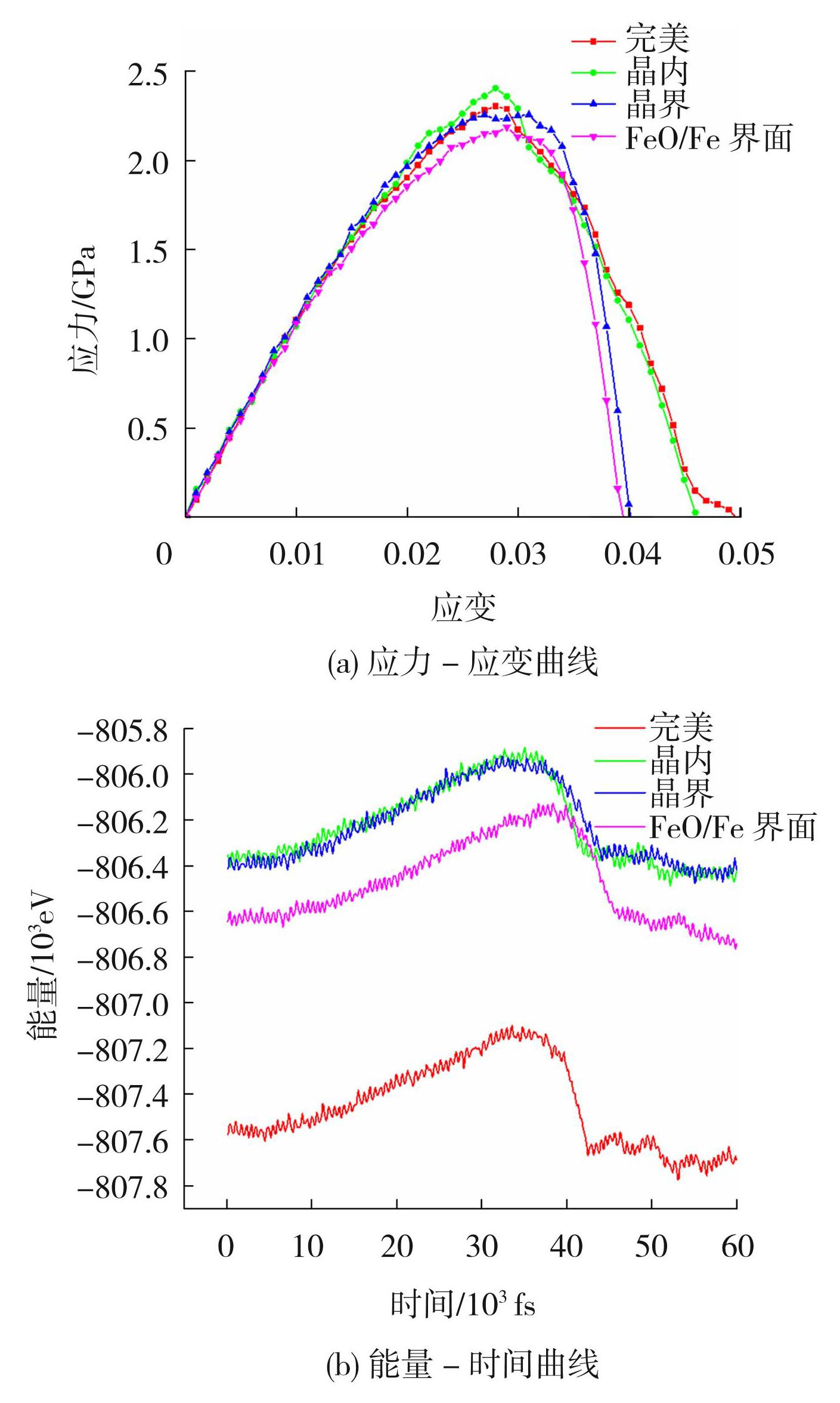
图3裂纹位于不同位置的曲线图
Fig.3Curves of cracks at different locations: (a) stress-strain curves; (b) energy-time curves
为进一步探究不同位置的裂纹对多晶FeO/Fe的影响,如图3(b)所示为裂纹位于不同位置时能量-时间变化曲线图。从图3(b)可以看出,整个模型能量变化呈现“上升→下降→稳定”的趋势,这是因为在单轴拉伸下,多晶FeO/Fe产生了一个应力集中区,随着拉应力的不断增加,模型内部的铁原子与氧原子开始活跃,整个模型的动能和势能从平衡态增加,因此整个模型的总能量上升,直至达到能量峰值。此时模型聚集了大量能量,当裂纹逐渐扩展直至断裂时,位错和微孔洞的萌生会吸收积聚的能量,随着裂纹尖端的位错不断发射和积聚的能量减少,最后会趋于一个稳定值。
位于不同位置的裂纹扩展CSP值示意图见图4,多晶FeO/Fe沿晶断裂和界面断裂示意图见图5,其中T=0 fs为多晶FeO/Fe模型弛豫完后初始状态,图4中A-D分别为不同模型裂纹扩展路径。从A、B、C、D处观察到整个模型断裂方式呈现两种形式,即沿晶扩展和界面脱粘;从CSP值可以看出,原子紊乱程度由高到低的区域依次为:裂纹处>原始晶界>原始FeO/Fe界面>原始多晶内部。在拉伸变形过程中,多晶Fe模型CSP值几乎无任何变化,应是由于Fe内部结合力远大于氧化皮模型多晶FeO,因此本文省去对多晶Fe模型的分析。
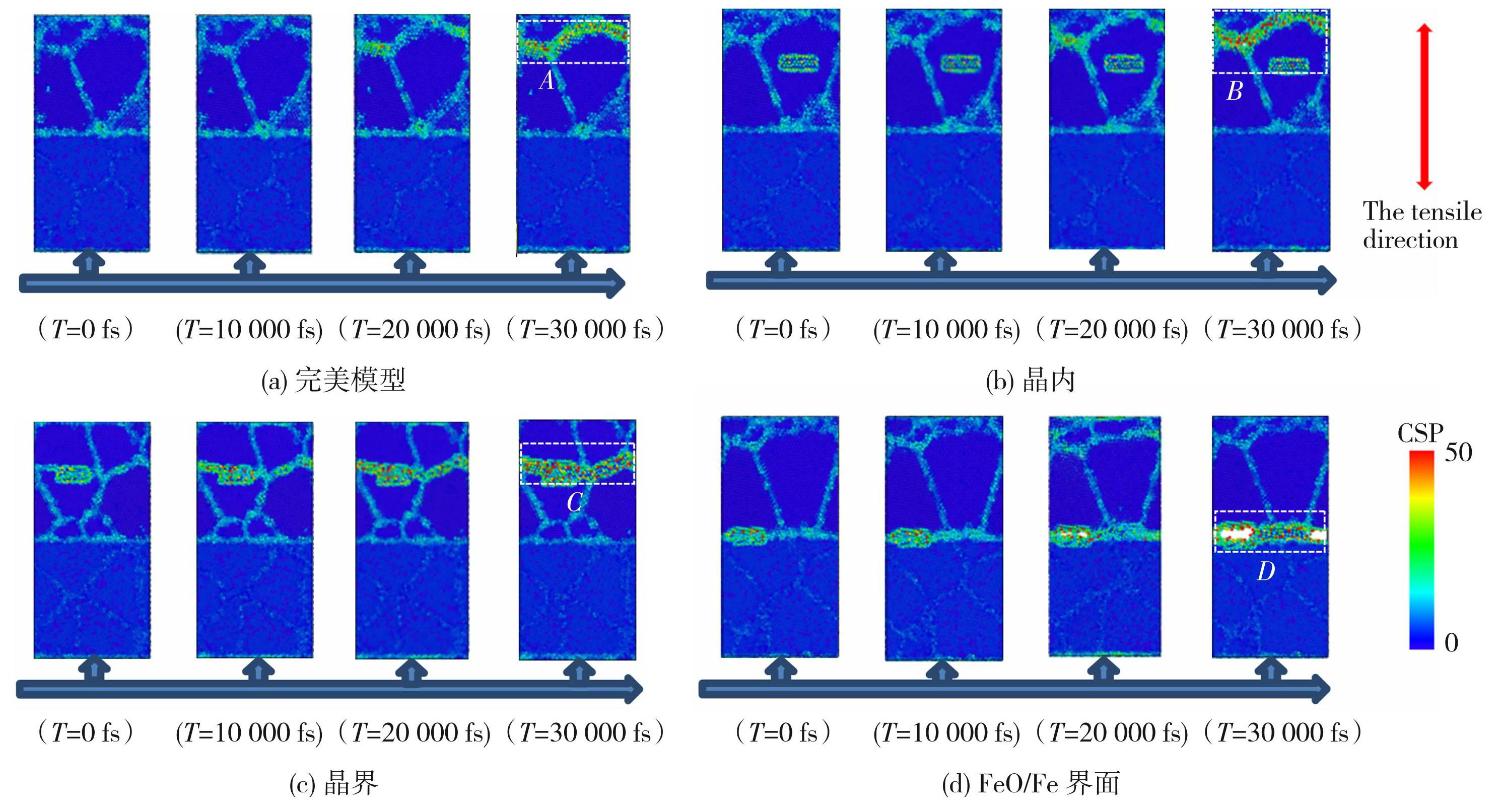
图4位于不同位置的裂纹扩展CSP示意图
Fig.4CSP growth at different locations: (a) perfect model; (b) intracrystalline; (c) grain boundary; (d) FeO/Fe interface
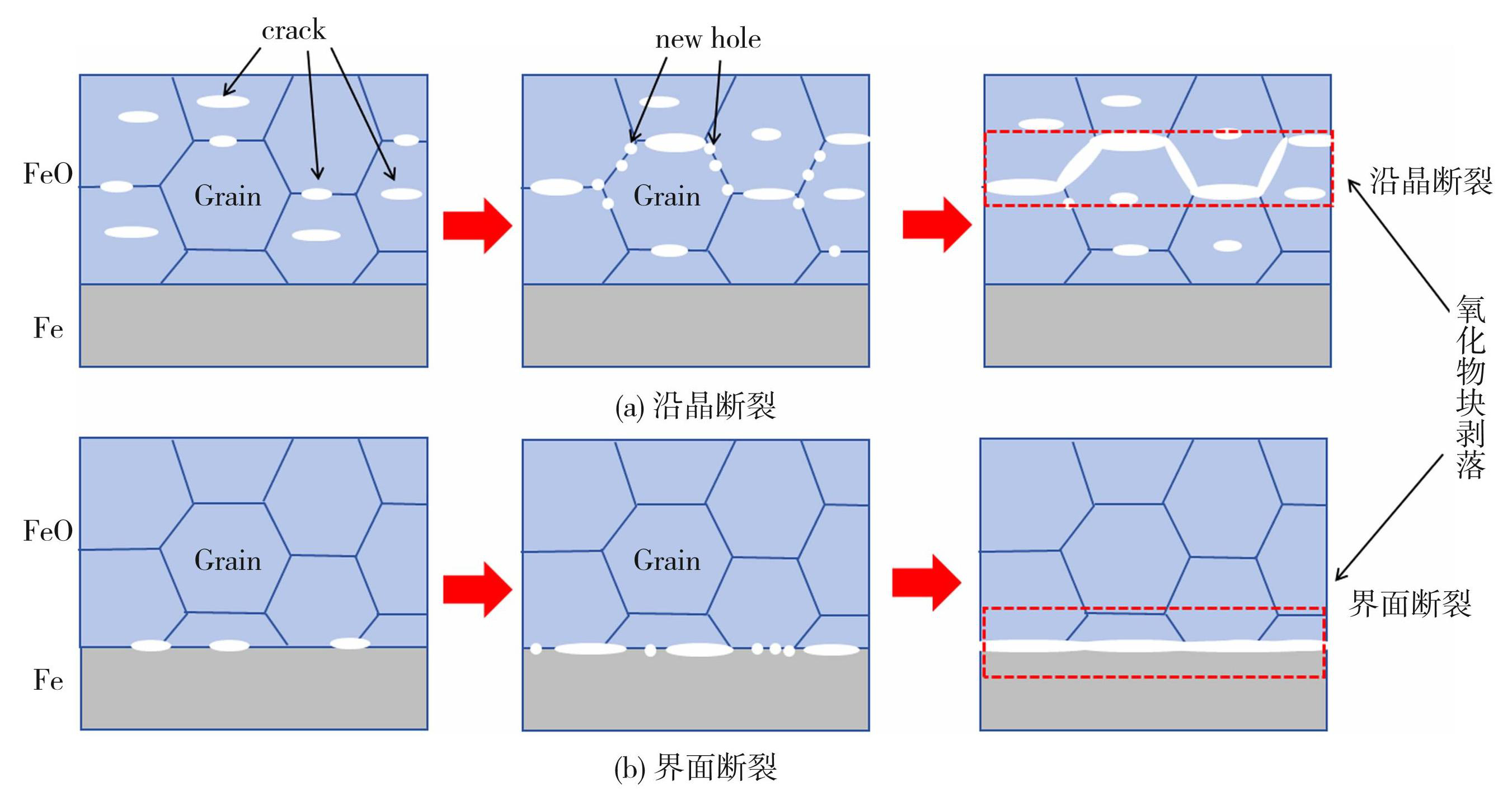
图5多晶FeO/Fe断裂示意图
Fig.5Schematic diagram of polycrystalline FeO/Fe fracture: (a) intergranular fracture; (b) interface fracture
裂纹位于晶内时模型裂纹扩展CSP示意图见图4(b),从图4可以观察到T=0~30 000 fs时,垂直于加载方向的晶界面处CSP值逐渐变大,原子颜色逐渐加深,晶界处应力容易集中,因此说明容易在此方向上产生位错。从局部区域B处发现,模型未从晶内裂纹处扩展,其原因是晶内裂纹尖端发射位错,位错之间相互缠绕和聚集,而晶界因原子排列不规则,存在畸变,同时作为“钉扎”中心,阻碍了位错的运动,致使FeO塑性变形更困难,因此增强了模型的抗拉强度,相比完美模型的抗拉强度更高,模型难以从晶内穿晶断裂,而在晶界处萌生新的微孔洞,拉应力作用下逐渐增大成微裂纹并沿晶扩展,从而出现沿晶断裂。
位于晶界的裂纹主要是沿晶断裂,在图4(c)中,由T=0 fs至T=20 000 fs可以看到,在拉应力下,裂纹尖端的原子颜色逐渐加深,红色原子变多。为了更好地理解裂纹位于FeO晶界时裂纹扩展及位错演化过程,图6(a)、(b)给出了T=20 000 fs时FeO内部位错演化和位错线分布图。从图6可以看到,位错大量分布在晶界,层错多发生在应力集中区。在拉伸下,裂尖出现应力集中和堆垛层错、发射位错。同时,随着时间的推移,位错缺陷和晶界上存在的晶格畸变相互作用,位错之间相互缠结,位错网络的初始镶嵌结构逐渐变得不规则,原子之间共价键的作用力减弱并逐渐变长至断裂,此时晶界处萌生出新的微孔洞,从图5(a)可以看到,随着时间的推移,晶界处微孔洞增大,微孔洞吸收大量的位错能,裂纹也逐渐沿晶界向两边扩展,促进了模型的断裂。
当裂纹位于FeO/Fe界面时,从图4(d)中T=20 000 fs时的图可观察到,模型达到应力峰值后,FeO/Fe界面处裂纹缺陷在拉应力作用下逐渐萌生出微孔洞,由图5(b)中的断裂示意图可以观察到孔洞逐渐增大,现存裂纹逐渐变大,两者联结成微裂纹并沿FeO/Fe界面处方向扩展,直至界面脱粘断裂为止。
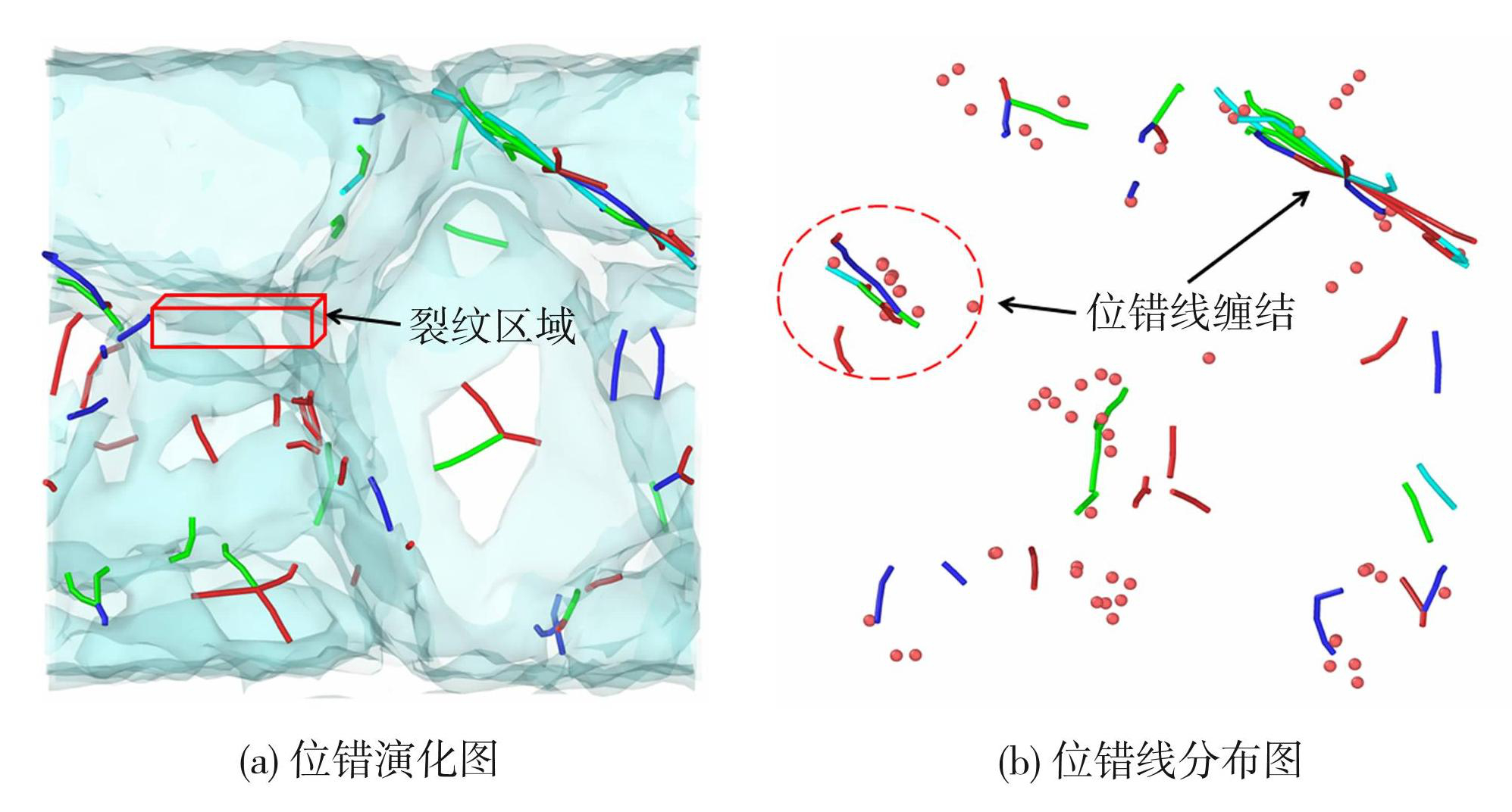
图6T=20 000 fs时裂纹位于晶界时位错演化及位错线分布图
Fig.6Evolution of dislocations and distribution of dislocation lines when crack located at grain boundary at T=20 000 fs: (a) dislocation evolution graph; (b) distribution of dislocation lines
综上所述,完美模型(即无缺陷模型)及裂纹位于晶内、晶界时,多晶FeO/Fe断裂变形为沿晶断裂,位于FeO/Fe界面时多晶FeO/Fe沿界面断裂。裂纹位于晶内时,模型出现沿晶断裂,晶界阻碍了裂纹尖端发射的位错传播,增强了模型的抗拉强度,达到2.41 GPa,使得模型难以断裂;裂纹位于晶界和FeO/Fe界面时,模型出现沿晶断裂和界面脱粘,裂纹处萌生出的微孔洞与现有裂纹相合并,促进了模型的断裂,降低了模型抗拉强度,使得模型更容易断裂。
2.2 应变率对多晶FeO/Fe拉伸力学性能的影响
为了研究应变率对含裂纹缺陷多晶FeO/Fe力学性能的影响,本文以裂纹缺陷位于FeO/Fe界面为研究对象。裂纹位于FeO/Fe界面处不同应变率下裂纹扩展CSP示意图见图7,M1-M5为模型断裂变形时刻局部放大图,P1-P3为裂纹局部区域放大图。随着应变率从图7(a)的1×109 s-1增加到图7(e)的1×1010 s-1,多晶FeO/Fe的裂纹扩展路径相同,但达到相同应变时,根据M1-M5局部放大图可以看到,FeO与Fe基体的断裂程度逐渐减小。
在弹性变形阶段,随着应变率升高,裂纹的扩展速度不明显,这是因为在拉伸载荷下,裂纹周围受力并不集中,而裂纹尖端出现了局部应力集中。以应变率为1×1010 s-1为例,当应变ε由0.01增加到0.03时,从P1-P3裂纹区域放大图可发现,裂纹缺陷原子颜色从蓝色→橙色→红色,且裂纹尖端红色原子逐渐增多,说明模型在受到拉应力作用下,原子逐渐紊乱,裂尖应力逐渐增大,继续扩展需克服更大阻力,产生钝化现象,促使裂纹张开,张开度逐渐增大,直至断裂。
图8(a)为裂纹位于FeO/Fe界面不同应变率下应力-应变曲线图,可看以到,模型在不同应变率下经历了弹性变形→塑性变形→断裂变形整个过程,变化趋势基本一致。当应变率从1×109 s-1增加到1×1010 s-1,位于FeO/Fe界面裂纹模型抗拉强度分别为2.21、2.59、2.78、3.08、3.25 GPa,可发现模型达到应力峰值时的极限应变逐渐增大,体现出与宏观尺度上类似的应变率效应,模型的抗拉强度也随着应变率的增高而增大,这是因为模型在达到应力峰值时,裂纹尖端原子颜色加深,出现应力集中,形成大区域的钝化原子,但晶界的滑移很难缓解应力集中现象,从而使得模型内部结构被严重破坏。
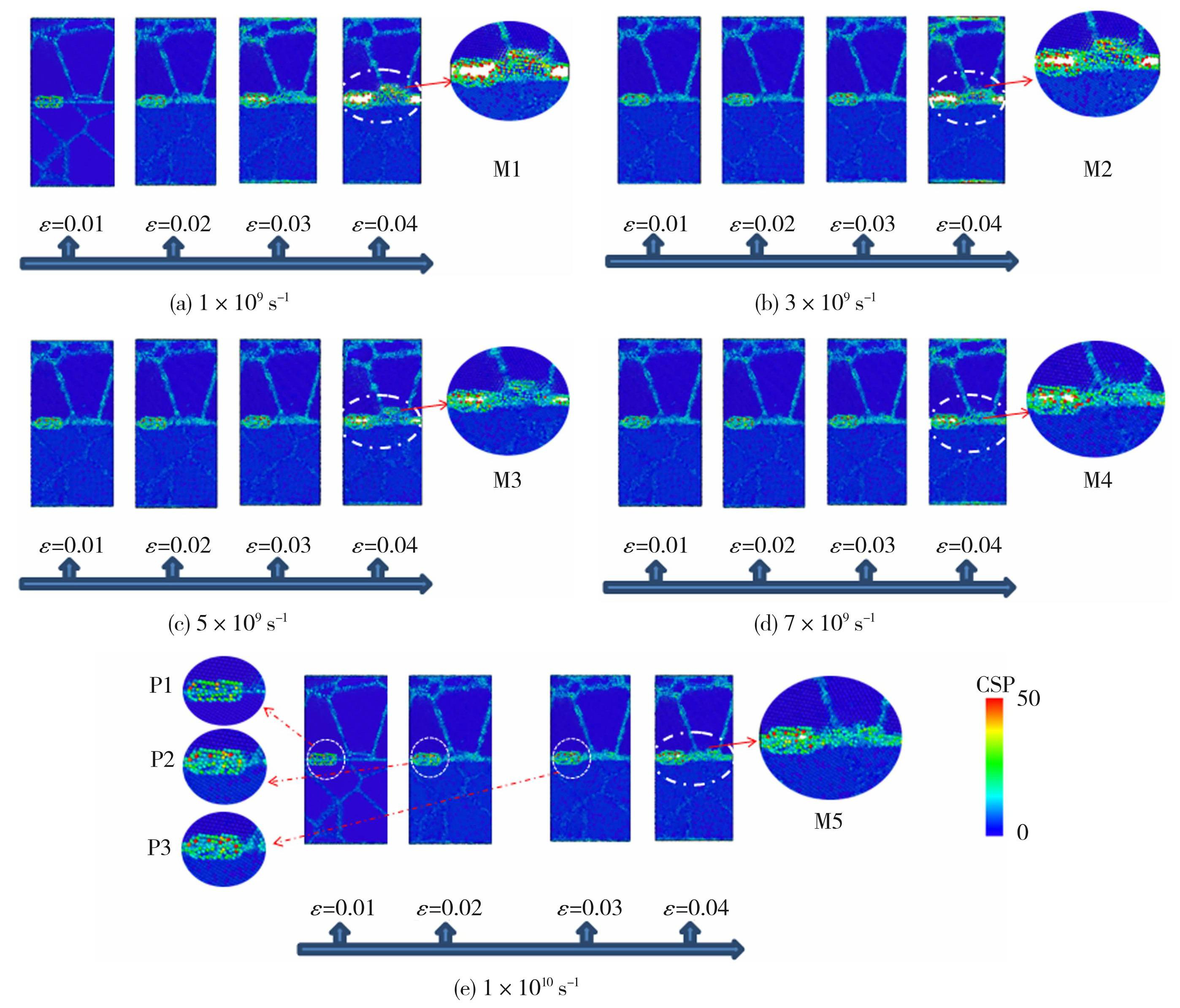
图7裂纹位于FeO/Fe界面不同应变率下裂纹扩展CSP示意图
Fig.7CSP diagram of crack growth at different strain rates at grain FeO/Fe interface
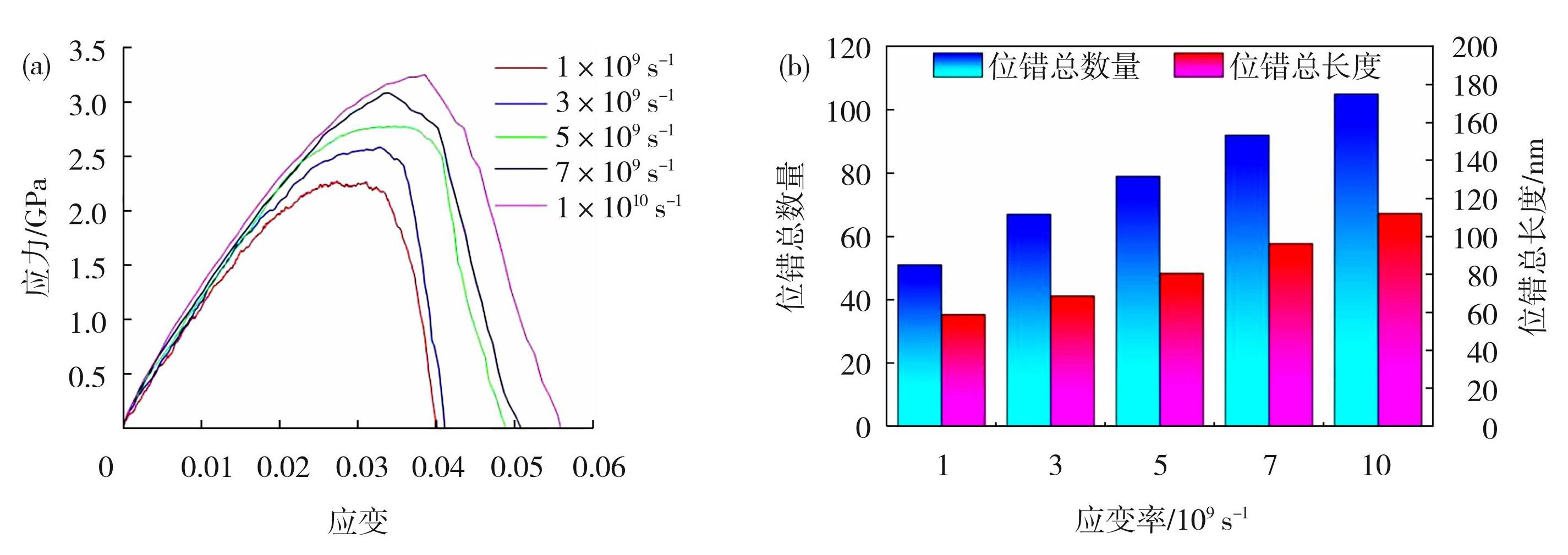
图8不同应变率下裂纹位于FeO/Fe界面时应力-应变曲线(a)及位错总数量与位错总长度图(b)
Fig.8Stress-strain curve for cracks at FeO/Fe interface under different strain rates (a) and graph of total number of dislocation count and total dislocation length (b)
在裂纹尖端处不仅出现钝化和滑移带,位错同时在裂纹尖端处逐渐增加,位错之间相互作用,形成了一个位错网络,阻止了裂纹尖端处原子继续紊乱,增强了模型的抗拉强度,减缓了模型的断裂,模型断裂程度越小,多晶FeO/Fe越难断裂。
为了更好解释上述现象的合理性,图8(b)所示为不同应变率下裂纹位于FeO/Fe界面时位错总数量和总长度曲线图,从图中可发现当应变率从1×109 s-1增加到1×1010 s-1时,位错总数量从51条增加至105条,总长度由58.78 nm增加至112.11 nm,呈现逐渐升高趋势。由此得知,多晶FeO/Fe内部抗变形力逐渐升高,产生的塑性变形程度增大,致使应力峰值逐渐升高,很好地解释了上述现象的合理性。
3 结论
1)从CSP值来看,原子紊乱程度从高到低的区域依次为裂纹缺陷、原始晶界、原始FeO/Fe界面及原始多晶内部。
2)当应变率一定时,裂纹位于不同位置时,多晶FeO/Fe中模型的断裂方式主要是沿晶断裂和界面断裂。裂纹位于完美模型、晶内、晶界和FeO/Fe界面的应力峰值分别为2.32、2.41、2.27、2.15 GPa。
3)当裂纹位于相同位置时,随着应变率从1×109 s-1增大到1×1010 s-1,多晶FeO/Fe模型的断裂程度逐渐变小,位错总数量从51条增加至105条,总长度从58.78 nm增加至112.11 nm,且应变率为1×1010 s-1下的抗拉强度比1×109 s-1的抗拉强度高近1 GPa,因此,应变率对多晶FeO/Fe模型的断裂变形程度影响更大,由此可以说明FeO/Fe的断裂变形存在应变率效应。
