2. 河北工程大学 机电工程学院, 056038 河北 邯郸
2. Machanical and Electrical Engineering Institure, Hebei University of Engineering, 056038 Handan, Hebei, China
车床在轴类及盘类零件加工中占有显要位置,我国数控车床主要存在精度低、精度保持性差等问题,影响机床精度的关键因素之一热误差占据机床总体误差的40%~70%[1],而对于高精密数控车床来说所占比重更大.近年来,国内外针对机床热特性的研究不胜枚举,也取得了一些良好的效果.杨军等[2-5]利用模糊聚类选择温度变量,建立了机床主轴热误差的BP神经网络模型、多元线性回归模型、最小二乘支持向量机模型及时间序列模型,并在多种工况下验证模型的准确性及鲁棒性;还有学者通过实验反求热流密度和热辐射等边界条件,提高机床热变形的仿真精度[6-8];Bossmanns等[9-10]利用有限差分模型分析并预测了电主轴热源的分布机理;Aguado[11]提出机床空间误差的测量方法;Heisel等[12]研究丝杠温度场分布,并建立了进给轴热误差模型;Guo和Shen等[13-14]利用不同的算法对BP神经网络模型进行了优化,提高了模型精度;径向基函数RBF(Radius Basis Function)的神经网络模型被广泛用于机床热误差建模中[15-16];Chen等[17-19]建立了主轴系统的多元线性回归模型.
现有文献都是针对主轴或进给轴单个系统分别建立模型,而且都是在理论上验证模型的准确性和鲁棒性,没有进行过实际的加工验证,实际加工中主轴与进给轴相互依赖共同影响工件的加工精度.本文针对HTC550/500车床建立主轴与进给轴的综合热误差模型,并进行补偿应用,并用实际加工来验证模型的准确性.
1 Siemens系统热误差补偿方式及热特性实验 1.1 Siemens系统热误差补偿方式Siemens开放了热误差补偿接口,一定温度下所开放的补偿模型为线性模型,主轴的热误差只与温度相关,与坐标位置无关;进给轴热误差不仅与温度相关,且与坐标位置相关.热误差模型原理图如图 1所示.
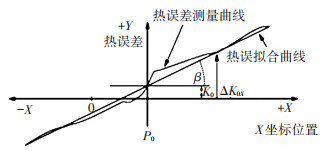
|
图 1 热误差补偿原理:温度θ下热误差的近似拟合线 |
Siemens内部模型:
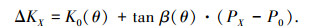
|
式中:ΔKX为在温度θ下PX处的热误差值, K0(θ)为温度θ下与位置无关的热误差值, tan β(θ)为温度θ下进给轴热膨胀系数, PX为当前位置坐标, P0热误差为零位置参考点.由此看出热误差补偿值是温度θ、坐标PX及P0共同作用的结果.
1.2 热特性实验 1.2.1 实验原理及方法以精密数控车床为研究对象,测试设备包括:RENISHAW激光干涉仪测量进给轴误差;自主设计的温度与位移同步采集系统测得温度及变形数据;传感器选用高精密温度传感器PT100和高精密电涡流传感器.采用五点法测量主轴空间变形[20],原理如图 2所示.
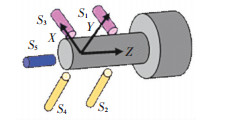
|
图 2 主轴热误差测量原理示意图 |
S1、S3为测量主轴X方向的热误差,S2、S4为测量主轴Y向的热误差,S5测量主轴Z向的热误差;文献4中详细介绍了利用激光干涉仪测量进给轴热误差的测量方法及注意事项,冷态下第一次测量进给轴误差为机床进给系统几何误差,进给系统连续往复运行20 min后测量误差值,此误差值减去几何误差作为此时进给系统热误差[4].
1.2.2 热特性分析进给轴电机、轴承、丝杠螺母副等摩擦生热导致丝杠温度升高,丝杠向自由端方向发生热膨胀引起丝杠导程变化.丝杠导程变化导致半闭环控制系统产生误差,进给轴的热误差变化如图 3所示.冷态下第1次测量值为机床的几何误差,故冷态下机床的热误差为0 μm.由图 3可以看出, 进给轴热误差不仅与温度相关, 而且与坐标位置相关,随坐标值的增大而增大;负向热误差变化相对较小,正向热误差变化相对较大,由此判断正向为进给轴自由端,即丝杠热膨胀的方向.
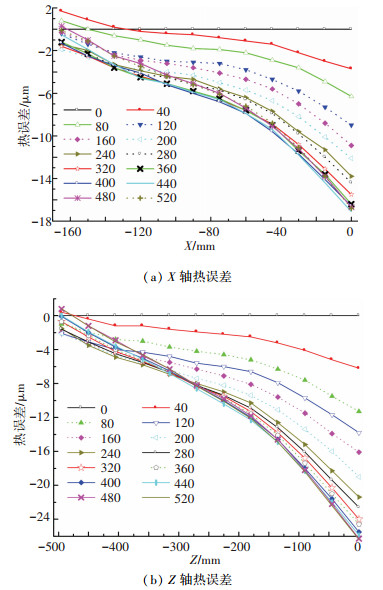
|
图 3 进给轴热误差曲线 |
主轴内部结构如图 4(a)所示,轴承摩擦生热,引起主轴及外壳温度升高,导致主轴发生热伸长Δz和热升高Δh.主轴热变形曲线如图 4(b)所示,主轴Z向热误差Δz最高达44 μm,X向热误差Δx最高达14 μm,随着温度的升高, 主轴的热变形随之增大,停机后随着温度的降低主轴的热变形随之减小.
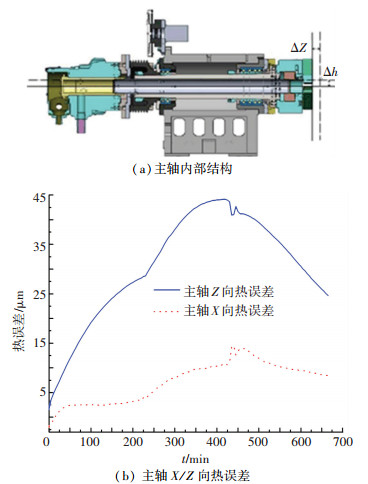
|
图 4 主轴结构示意图及主轴X/Z向热误差 |
机床热特性实验主轴及进给轴温度变化见图 5.
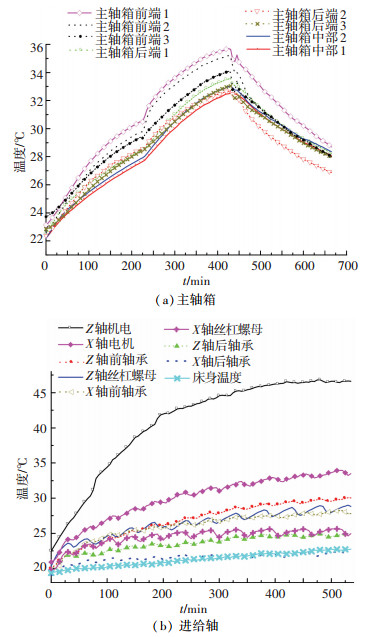
|
图 5 主轴与进给轴温度场变化 |
主轴传感器PT100配置前端3个、中部2个、后端3个,前端最高温度达35.9 ℃、后端33.8 ℃、中部32.8 ℃,其中前部最高温差13.2 ℃、后端12.1 ℃、中部10.8 ℃.主轴内部结构如图 4(a)所示,循环空气冷却中空式结构,前端3个轴承后端1个,导致前端发热量最大,后端次之,中部最小,温度场变化与结构相符合.由图 5(a)和图 4(b)对比可看出, 曲线变化规律一致,变形与温度之间具有一定的线性关系.
进给轴传感器PT100配置主要在电机、轴承及丝杠螺母座上,通过螺母座温度间接反映丝杠温度变化.其中,电机温度变化最大,床身温度变化最小;前轴承温度大于后轴承;Z轴螺母座温度大于X轴螺母座.
2 热误差建模及补偿实现 2.1 综合热误差建模本文采用的建模方法为MLRA模型,建立热误差与温度变量之间的变化关系,设因变量y与自变量x=(x1, x2, …, xm),其中y为热误差,x为温度变量,MLRA可以表示为
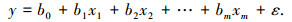
|
式中:b0, b1, …, bm为待定参数,ε为随机误差.
在车床加工过程中,主轴与进给轴热误差相互耦合共同影响工件的精度,因此需要建立主轴与进给轴的综合热误差模型.
2.1.1 主轴热误差模型主轴热特性实验中, 电涡流传感器的安装位置影响测量结果,以X向热误差测量为例说明. 图 6为主轴热特性实验传感器安装主轴轴向视图.
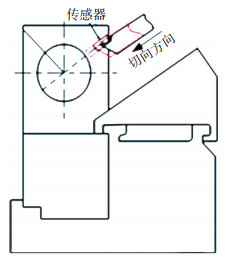
|
图 6 传感器安装主轴轴向示意图 |
传感器的安装支架安装在刀塔上.实验过程非恒温,环境温度的升高导致丝杠温度升高,并伴随着热伸长,X轴丝杠热伸长导致刀塔位置发生变化,从而引起传感器相对于测量芯棒的位置变化,导致传感器测量主轴X向热误差就包含了X轴丝杠热变形误差.因此,主轴X向热误差建模中要消除X轴丝杠的热变形误差,处理方法:
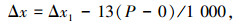
|
其中: Δx1为测量值,P为实验中X轴坐标值,13为钢的理论膨胀系数.
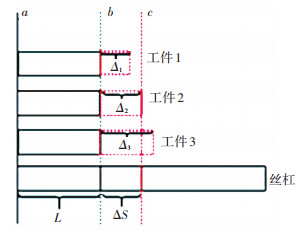
2.1.2 进给轴热误差模型由于轴承及丝杠螺母副摩擦发热,丝杠温度升高导致进给系统产生热误差.然而, 在实际加工中工件也会发生热胀冷缩现象,同样会影响工件的加工精度. 图 7为工件与丝杠变形示意图.相同温度下所有工件的长度均为L,在相同温升条件下工件1、2、3的膨胀量分别为Δ1、Δ2、Δ3,丝杠在相同长度L上的膨胀量为ΔS.当工件的膨胀系数<丝杠的膨胀系数,即当ΔS>Δ1时,丝杠的膨胀量大于工件的膨胀量,此时的补偿量为丝杠与工件膨胀量的差值,方向为丝杠膨胀反方向;当丝杠的膨胀系数等于工件的膨胀系数,即当ΔS=Δ2时,丝杠的膨胀量与工件膨胀量相同,此时丝杠的膨胀量刚好补偿了工件的膨胀量,不需要对丝杠的膨胀量进行补偿;当丝杠的膨胀系数小于工件的膨胀系数,即ΔS<Δ3时,丝杠的膨胀量小于工件的膨胀量,此时的补偿量亦为丝杠与工件膨胀量的差值,方向为丝杠膨胀方向.因此,进给轴的热误差补偿要考虑工件的膨胀效应,补偿方法:
|
图 7 工件与丝杠变形示意图 |
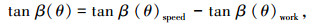
|
其中:tan β(θ)speed为进给轴补偿量,tan β(θ)work为工件补偿量.
2.1.3 综合热误差模型选取主轴及床身温度为温度变量,结合MLRA方法得到如下主轴的热误差模型:
主轴X向热误差为
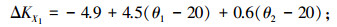
|
(1) |
主轴Y向热误差为
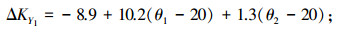
|
(2) |
X轴热误差为
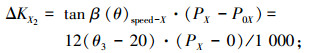
|
(3) |
Z轴热误差为
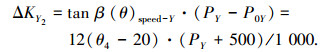
|
(4) |
式中:θ1、θ2、θ3、θ4分别为床身、主轴、X轴螺母和Z轴螺母温度;tan β(θ)speed-X、tan β(θ)speed-Y分别为X、Y轴丝杠膨胀系数;PX、PY为进给轴坐标;P0X、P0Y为进给轴参考点坐标值.模型中将20 ℃作为参考温度是因为GB中将20 ℃作为检测时标准环境温度,机床定位精度检测标准环境温度亦为20 ℃.
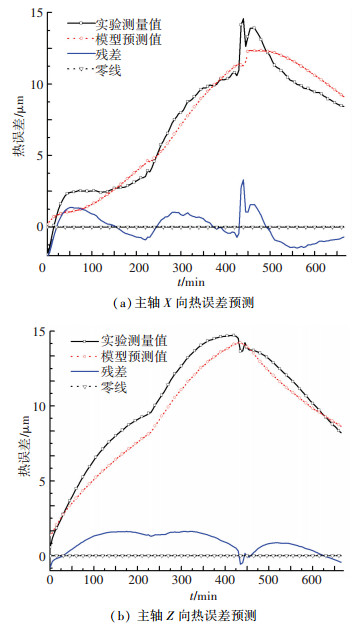
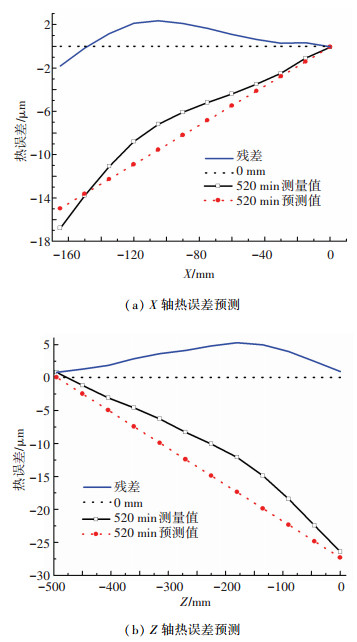
图 8、9为主轴及X/Z进给轴热误差模型预测值与实验值的对比图.建立模型预测精度评价标准均方根误差值RMSE及预测精度η[5].其中R为均方根误差值, yi为实验测量值, 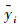
|
图 8 主轴热误差模型预测值与测量值的比较 |
|
图 9 进给轴热误差模型预测值与测量值的比较 |

|
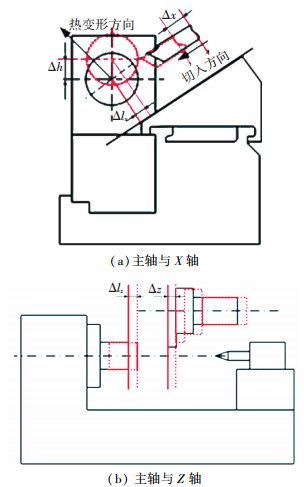
机床主轴系统与进给轴系统为相对独立的个体,实际加工中二者缺一不可,轴与进给轴的热误差相互关联共同影响工件的加工精度.得到主轴与进给轴热误差的相互关系对于模型的建立尤为重要.主轴系统由于轴承及加工摩擦生热造成主轴系统温度升高,随之产生热变形Δlz、Δh,丝杠受热发生膨胀导致进给系统产生热误差Δx、Δz,如图 10所示.由于X轴是倾斜式安装,主轴热变形Δh在机床X方向产生分量Δlx,方向与X进给轴相同;主轴热伸长Δlz方向与Z进给轴方向相同.因此机床X/Z方向的热误差模型应该是主轴与进给轴的综合热误差模型.结合式(1)~(4)及文章2.2.1、2.2.2节分析得到机床在X/Z方向的综合热误差模型.
|
图 10 主轴与进给轴热误差耦合示意图 |
X方向热误差模型:
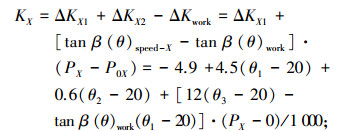
|
(8) |
Y方向热误差模型:
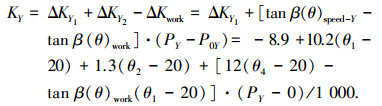
|
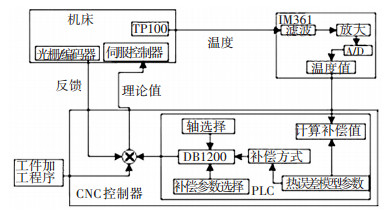
Siemens828D热误差补偿总体方案如图 11所示,由PLC直接获取机床热源温度值,在PLC内计算补偿参数,最后PLC通过数据接口DB1200将补偿参数写入NC系统内,系统根据补偿参数及插补指令计算正确的电机指令从而达到补偿效果,提高机床的加工精度.
|
图 11 Siemens828D热误差补偿总体方案 |
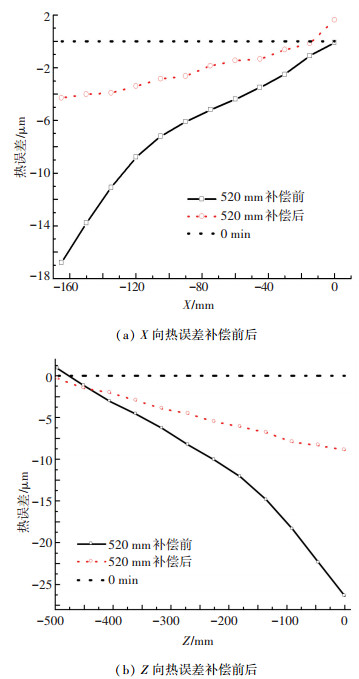
冷态下测量机床的定位精度,随后同时运转主轴及进给轴系统,模拟实际加工主轴与进给轴热误差耦合现象,验证综合热误差模型的准确性,直到机床达到热平衡状态.测量机床热误差补偿前后的定位精度,结果如图 12所示.热补偿前X/Z轴定位精度分别为19.8 μm、27.2 μm;热补偿后X/Z轴定位精度分别为6.9、9.1 μm,热补偿后X/Z轴定位精度分别提高了65.2%、68.4%,表明热误差综合模型有一定的补偿效果.
|
图 12 X/Z轴热平衡下热误差补偿前后对比 |
加工工件如图 13所示,严格按照工程实际在有无热误差补偿状态下按图纸要求进行加工,两种状态下各加工一天,对工件按照加工顺序做编号.将加工好的工件置于20 ℃的恒温环境中8 h以上,按编号使用三坐标测量仪测量工件R1、R2的直径,记录于表格,比较有无热误差补偿状态下的工件误差.

|
图 13 加工工件 |
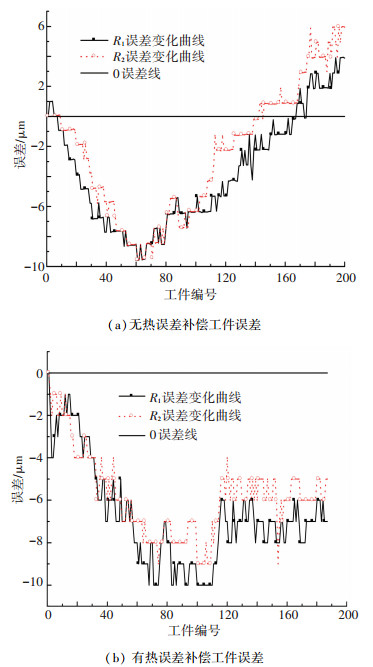
实际结果如图 14所示.由图 14可知,在有无热误差补偿状况下工件误差首先负向变大而后向正向变化,这是由于X轴丝杠的安装在X负向有预拉伸,丝杠温升初始时首先要消耗预拉伸量,因此导致工件误差负向变化. 图 14(a)所示预拉伸消耗之后工件误差正向有明显变化,跨度15 μm,这便是热误差造成的影响;图 14(b)所示预拉伸消耗之后工件误差有了明显改善,跨度5 μm左右,由此证明热误差补偿的准确性.
|
图 14 有无热误差补偿时的工件误差 |
1) 本文研究了Siemens828D系统的热误差补偿机制,分析了主轴与进给轴热误差之间的相互关系,建立了综合热误差模型,并考虑了工件的膨胀效应对模型的影响.
2) 利用PLC与NC之间的数据接口DB1200实现了补偿数据的通信,加工过程中监测温度并进行实时补偿.
3) 并进行了切削加工试验,有效验证了热误差的补偿效果.
| [1] |
BRYAN J B. International status of thermal error research[J]. Annals of CIRP, 1990, 39(2): 645-656. DOI:10.1016/S0007-8506(07)63001-7 |
| [2] |
YANG Jun, SHI Hu, FENG Bin, et al. Applying Neural Network based on fuzzy cluster pre-processing to thermal error modeling for Coordinate Boring Machine[J]. Proceedings of the 47th CIRP Conference on Manufacturing Systems. Windsor: [s. n. ], 2014: 698-703.
|
| [3] |
YANG Jun, ZHANG Dongsheng, FENG Bin, et al. Thermal-induced errors prediction and compensation for a coordinate boring machine based on time series analysis[J]. Mathematical Problems in Engineering, 2014(6): 1-13. |
| [4] |
杨军, 施虎, 梅雪松, 等. 双驱伺服进给系统热误差的试验测量与预测模型构建[J]. 西安交通大学学报, 2013, 47(11): 53-59. DOI:10.7652/xjtuxb201311010 |
| [5] |
杨军, 梅雪松, 赵亮, 等. 基于模糊聚类测点优化与向量机的坐标镗床热误差建模[J]. 上海交通大学学报, 2014, 48(8): 1175-1182. |
| [6] |
JARNYY, OZISKI M N, BARDON J P. A general optimization method using adjoint equation for solving multidimensional inverse heat conduction[J]. International Journal of Heat Mass Transfer, 1991, 34(11): 2911-2919. DOI:10.1016/0017-9310(91)90251-9 |
| [7] |
MONDE M. Analytical method in inverse heat transfer problem using Laplace transform technique[J]. International Journal of Heat Mass Transfer, 2000, 43(21): 3965-3975. DOI:10.1016/S0017-9310(00)00040-5 |
| [8] |
JALALI-HERAVI M, FATEMI M H. Prediction of thermal conductivity detection response factors using an artificial neural network[J]. Journal of Chromatography A, 2000, 897(1/2): 227-235. |
| [9] |
BOSSMANNS B, TU J F. A thermal modle for high speed motorized spindles[J]. International Journal of Machine Tools and Manufacture, 1999, 39(9): 1345-1366. DOI:10.1016/S0890-6955(99)00005-X |
| [10] |
BOSSMANNS B. Thermo-mechanical modeling of motorized spindle systems for high speed milling[D]. West Lafayette: Purdue University, 1997: 53-81.
|
| [11] |
AGUADO S, SAMPER D, SANTOLARIA J, et al. Identification strategy of error parameter in volumetric error compensation of machine tool based on laser tracker measurements[J]. International Journal of Machine Tools and Manufacture, 2012, 53(1): 160-169. DOI:10.1016/j.ijmachtools.2011.11.004 |
| [12] |
HEISEL U, KOSCSÁk G, STEHLE T. Thermography based investigation into thermally induced positioning errors of feed drives by example of a ball screw[J]. CIRP Annals-Manufacturing Technology, 2006, 55(1): 423-426. DOI:10.1016/S0007-8506(07)60450-8 |
| [13] |
GUO Q J, YANG J G, WU H. Application of ACO-BPN to thermal error modeling of NC machine tool[J]. International Journal of Advanced Manufacturing Technology, 2010, 50(5): 667-675. |
| [14] |
SHEN J H, YANG J G. Application of partial least squares neural network in thermal error modeling for CNC machine tool[J]. Key Engineering Materials, 2009, 392-394: 30-34. |
| [15] |
张宏韬, 杨建国. RBF网络在线建模方法在热误差实时补偿技术中的应用[J]. 上海交通大学学报, 2009, 43(5): 807-810. DOI:10.3321/j.issn:1006-2467.2009.05.026 |
| [16] |
LI X. Real-time prediction of workpiece errors for a CNC turning centre, Part 2. Modelling and estimation of thermally induced errors[J]. International Journal of Advanced Manufacturing Technology, 2001, 17(9): 654-658.
|
| [17] |
CHEN J S, WEI Y H. Characterizations and models for the thermal growth of a motorized high speed spindle[J]. International Journal of Machine Tools and Manufacture, 2003, 43(11): 1163-1170. DOI:10.1016/S0890-6955(03)00103-2 |
| [18] |
CHEN J S. A study of thermally induced machine tool errors in real cutting conditions[J]. International Journal of Machine Tools and Manufacture, 1996, 36(12): 1401-1411. DOI:10.1016/0890-6955(95)00096-8 |
| [19] |
CHEN J S, YUAN J, NI J. Thermal error modeling for real-time error compensation[J]. International Journal of Advanced Manufacturing Technology, 1996, 12(4): 266-275. DOI:10.1007/BF01239613 |
| [20] |
International Organizatin for Standardization. ISO 230-3: 2007(E) Test code for machine tools Part 3: Determination of thermal effects[S]. Generva: ISO copyright office, 2007.
|
 2016, Vol. 48
2016, Vol. 48


