2. 三峡大学 电气与新能源学院, 443002 湖北 宜昌
2. College of Electrical Engineering and Renewable Energy, China Three Gorges University, 443002 Yichang, Hubei, China
工程粗糙表面特别是切削表面, 是挤压和撕裂、弹性变形和塑性变形、热和力等因素综合作用的结果, 其微观形貌通常是极不规则与粗糙不平的.柔性结合部是由2个切削加工的粗糙表面接触形成的, 柔性结合部接触问题的实质是粗糙表面间的接触问题.在微观上, 粗糙表面实际存在着多个凸起, 而对于其中的每个凸起, 均可以将其近似等效为一个半球体.柔性结合部在机械结构中大量存在, 当受到动载荷作用时, 柔性结合部会产生微小的相对线位移或角位移, 使柔性结合部既存储能量又消耗能量, 表现出既有弹性又有阻尼, 即存在接触刚度和接触阻尼, 严重影响机械结构的静、动态特性[1-20].接触刚度和接触阻尼构成宏观、微观接触中的弹簧-阻尼模型.机械零件结合部可视为两粗糙表面相互接触而成, 通常采用法向接触刚度和接触阻尼等参数来表征结合部的法向特性.当结合部之间受到法向载荷作用时, 在粗糙表面的凸起产生变形, 一部分凸起的接触面积超过临界接触面积而处于弹性变形状态, 储存了弹性应变能, 表现为法向刚度作用; 另一部分凸起的接触面积未超过临界接触面积而产生塑性变形状态, 耗散了系统的能量, 从而展现为法向阻尼作用.结合部有可能表现出既有弹性又有阻尼, 既储存能量又消耗能量的“柔性结合”的本质及特性.
对于机床、齿轮箱与动力机械, 其总阻尼的90%以上来源于柔性结合部的接触阻尼.与机械零件本身的阻尼相比, 柔性结合部接触阻尼占绝对优势, 对机械和机械结构的静动态特性具有重要影响.田红亮等[21]利用Hertz法向接触力学方程和修订分形几何学理论评估柔性结合部的法向接触刚度、法向接触阻尼, 但存在着如下的3个缺憾:1)未给出凸起顶端曲率半径与变形量之间的内在联系; 2)推导法向接触阻尼方程时, 仍然假设凸起顶端的曲率半径为常数; 3)作用在凸起上的法向接触载荷在临界接触点面积处出现跳跃间断点.
本文以本项目组所做的部分工作[1-21]为基础, 考虑凸起顶端的曲率半径为变量与凸起承受法向接触载荷的连续性, 深度架构一种新颖的柔性结合部法向接触阻尼方程.
1 修正分形几何学理论 1.1 凸起分担的法向弹性接触载荷对机械加工表面形貌进一步研究发现, 粗糙表面具有处处不平滑、不可微分的特性, 并且随着测量分辨率的不断提高, 会不断出现具有统计自相似的、更为精细的结构.在所有实数的定义域内, 全体点连续、到处不可求导并具有统计学自相似性的Weierstrass-Mandelbrot分形函数[22]为
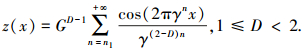
|
(1) |
式中:x为轮廓位移坐标, G为分形粗糙度, D为表面粗糙轮廓分形维数, n为频率因子, n1为最低频率的初始项, γ为缩放参数.
据式(1)可得凸起顶端的变形量为
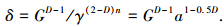
|
(2) |
式中a为凸起接触点面积,且
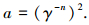
|
(3) |
通过式(2)、(3)可得Hertz凸起顶端的曲率半径为
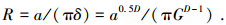
|
(4) |
凸起承担垂直于柔性结合部的法向弹性接触载荷为
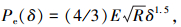
|
(5) |
将式(4)和(2)代入式(5)得
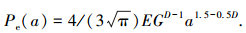
|
(6) |
凸起的弹塑性接触面积[20]见式(7):
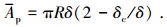
|
(7) |
式中:δc为凸起发生弹-塑性变形转化的临界变形量.
若δc

|
(8) |
由式(4)得
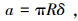
|
(9) |
将式(9)代入式(8)得式(10):
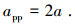
|
(10) |
凸起负担垂直于柔性结合部的法向完全塑性接触载荷为
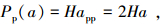
|
(11) |
式(11)不同于文献[21]中的式(13): Pp(a)=Ha.
1.3 干摩擦结合部担当的法向接触总载荷凸起发生弹-塑性变形转化的临界变形量[1]为
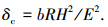
|
(12) |
式中:b为待定常数, E为复合弹性模量, H为较软材料的硬度.
将式(4)代入式(12)得
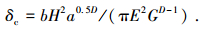
|
(13) |
式(2)除以式(13)得式(14):
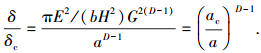
|
(14) |
式中ac为临界接触点面积, 并且
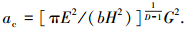
|
(15) |
临界接触点面积ac在式(6)中相应的凸起法向弹性接触载荷为
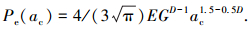
|
(16) |
式(16)与文献[2]中的式(38): Pe(ac′)=4/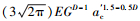
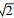
临界接触点面积ac在式(11)中对应的凸起法向完全塑性接触载荷为
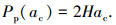
|
(17) |
如果作用在凸起上的法向接触载荷在临界接触点面积ac处保持连续, 能令Pe(ac)=Pp(ac), 则式(17)变为
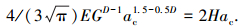
|
(18) |
将式(15)代入式(18)得
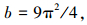
|
(19) |
将式(19)代入式(12)得
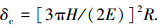
|
(20) |
式(20)不同于文献[21]中的式(5):
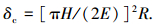
|
将式(19)代入式(15)得
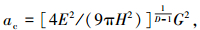
|
(21) |
式(21)不同于文献[21]中的式(8):
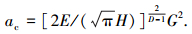
|
凸起接触点面积a的分布密度函数为
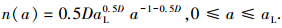
|
(22) |
式中aL为最大接触点面积.
据式(22)可得柔性结合部的实际接触总面积为
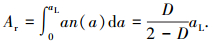
|
(23) |
令aL>ac, 柔性结合部的法向接触总载荷为

|
(24) |
式(24)不同于文献[21]中的式(14).
将式(22)代入式(24)得
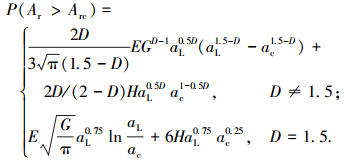
|
(25) |
式中: Arc=D/(2-D)ac为实际临界接触面积.式(25)不同于文献[21]中的式(15).
根据式(23)得
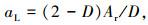
|
(26) |
将式(26)代入式(25)得
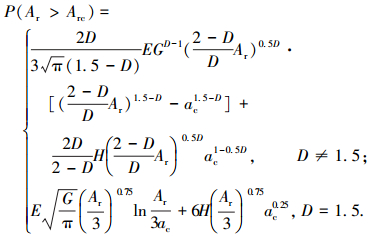
|
(27) |
式(27)不同于文献[21]中的式(17).
由式(27)可得归一化法向接触总载荷为
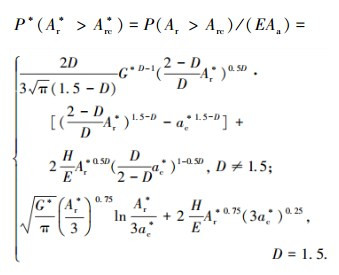
|
(28) |
式中: Ar*=Ar/Aa; Arc*=Arc/Aa=Dac*/(2-D); Aa为名义接触面积; G*=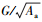
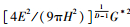
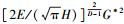
将式(9)代入式(4)得
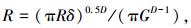
|
(29) |
由式(29)可得凸起顶端曲率半径和其变形量之间的内在关系为
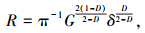
|
(30) |
将式(30)代入式(5)得
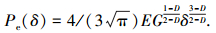
|
(31) |
式(31)比文献[2]中的式(64): Pe(δ)=4/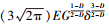
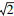
法向弹性接触载荷对凸起顶端变形量的1阶导函数, 即为2个凸起之间互相影响的法向接触刚度
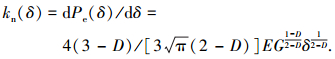
|
(32) |
式(32)比文献[2]中的式(65):dPe(δ)/dδ=4(3-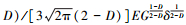
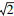
将式(2)代入式(32)得
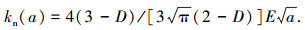
|
(33) |
式(33)比文献[2]中的式(66):kn(a′)=4(3-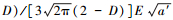
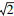
根据式(33)可得柔性结合部的法向接触总刚度为
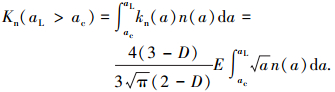
|
(34) |
将式(22)代入式(34)得
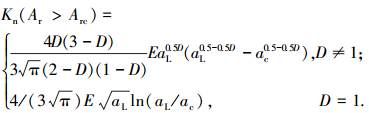
|
(35) |
将式(26)代入式(35)得
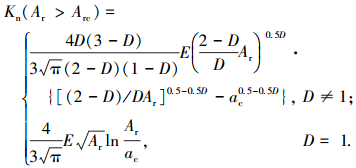
|
(36) |
按照式(36)可得归一化法向接触总刚度为
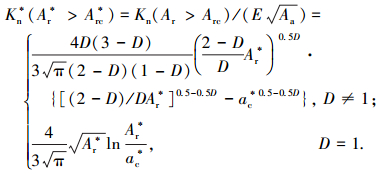
|
(37) |
将式(9)代入式(11)得

|
(38) |
式(38)不同于文献[21]中的式(28):

|
将式(30)代入式(38)得
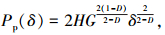
|
(39) |
由式(39)可得凸起压缩时的塑性损耗能
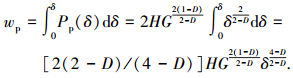
|
(40) |
将式(2)代入式(40)得

|
(41) |
式(41)不同于文献[21]中的式(31):
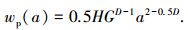
|
使用式(41)可得柔性结合部的塑性总损耗能为
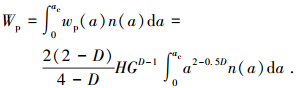
|
(42) |
式(42)不同于文献[21]中的式(32):
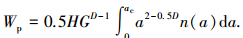
|
将式(22)代入式(42)得
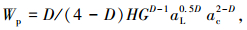
|
(43) |
式(43)不同于文献[21]中的式(33):
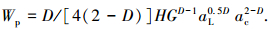
|
由式(31)可得凸起压缩时的弹性势能为
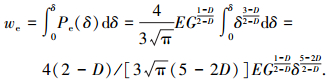
|
(44) |
将式(2)代入式(44)得
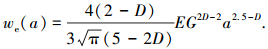
|
(45) |
式(45)不同于文献[21]中的式(36):
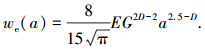
|
依据式(45)可得柔性结合部的弹性总势能为
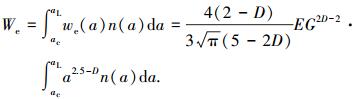
|
(46) |
式(46)不同于文献[21]中的式(37):
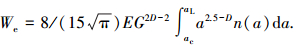
|
将式(22)代入式(46)得
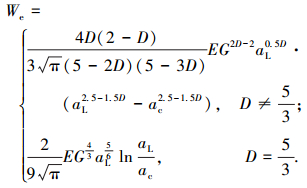
|
(47) |
式(47)不同于文献[21]中的式(38).
式(43)除以式(47)可得柔性结合部的结构阻尼损耗因子为

|
(48) |
式(48)不同于文献[21]中的式(39).
将式(26)代入式(48)得
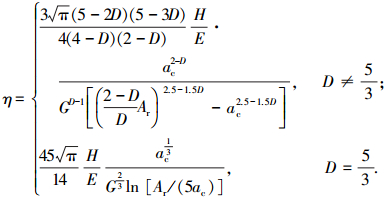
|
(49) |
式(49)不同于文献[21]中的式(40).式(49)可变形为
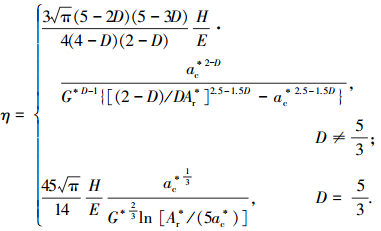
|
(50) |
式(50)不同于文献[21]中的式(41).
设粗糙表面专属基体虚拟材料[18]的质量为m, 则柔性结合部的法向接触阻尼为
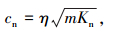
|
(51) |
由式(37)得

|
(52) |
将式(52)代入式(51)得
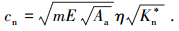
|
(53) |
由式(53)可得归一化法向接触阻尼为
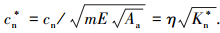
|
(54) |
将式(50)和(37)代入式(54)得

|
(55) |
式(55)不同于文献[21]中的式(46).
4 机械干摩擦结合部阻尼模拟灰铸铁是指石墨呈片状分布的灰口铸铁.灰铸铁组成(质量分数)为2.5%~4.0%C, 1.0%~3.0%Si, 0.25%~1.0%Mn, 0.05%~0.50%P, 0.02%~0.20%S.灰铸铁主要用于制造承受压力和振动的零部件, 如机床床身、各种箱体、壳体、泵体、缸体等.两配对灰铸铁HT250(单铸试棒的最小抗拉强度是250 MPa)干摩擦结合部的参数为[23]: 918HBW1/30/20, 表示用直径1 mm的硬质合金球在294.21 N试验力下保持20 s测定的布氏硬度值为918, 较软材料的布氏硬度H=9.8×918 MPa=8 996.4 MPa≈9 GPa, 弹性模量E1=E2=197 GPa, 泊松比ν1=ν2=0.49, 则复合弹性模量[24-44]E=129.6≈130 GPa, 表面粗糙轮廓分形维数D∈[1.12, 1.99], 名义接触面积Aa=10-6 m2, 分形粗糙度G取10-10~10-17 m, 则G*[45-48]取10-7~10-14.
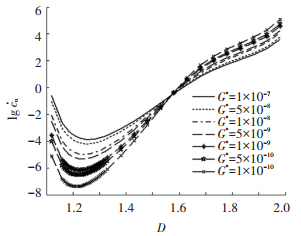
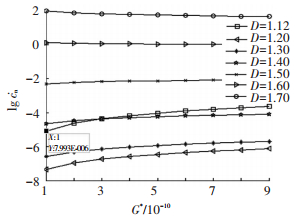
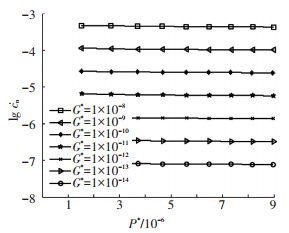
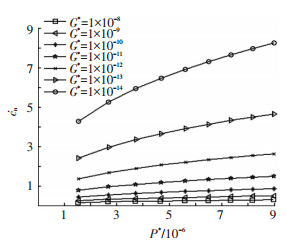
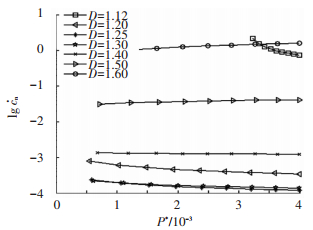
图 1~7为法向接触阻尼的演化状况.从图 1~3、6、7中可看出, 法向接触阻尼随着表面粗糙轮廓分形维数的增加而先变小后增加, 最小值点为D=1.26(图 1), 与图 2中的左上角曲线最小值点(1.26, 0.000 133 8)一致.由图 1可知, 法向接触阻尼-表面粗糙轮廓分形维数曲线具有2个拐点, 第1拐点为D1=1.58, 第2拐点为D2=1.92.分形粗糙度对法向接触阻尼的影响与第1拐点D1的大小有关.拐点是曲线凹凸性的分界点, 在图 2中, 最低点处的数值变化较快, 为了能够清楚地表达各量之间的关系, 在最低点处对点的数量进行加密.从图 2~4中可看出, 当D≤D1时, 法向接触阻尼随着分形粗糙度的变大而变大.图 3中, 当D=1.12时, G*=1×10-10时所对应的cn*的值为7.993×10-6, 与图 2中推算出来的坐标值(1.12, 7.993×10-6)相同.从图 2、3、5中可看出, 当D>D1时, 分形粗糙度越大, 法向接触阻尼反而越小.法向接触载荷对法向接触阻尼的影响与表面粗糙轮廓分形维数的大小有关.从图 4、6中可看出, 当D≤1.4时, 法向接触阻尼随着法向接触载荷的增加呈稍许减小的态势.从图 5~7中可看出, 当D>1.4时, 法向接触阻尼随着法向接触载荷的增大而增加, 文献[21]未推测出此种演变情况.

|
图 1 Ar*=0.1, G*=10-7时阻尼与分形维数的关系 |
|
图 2 不同G*,且Ar*=0.1时阻尼与分形维数的关系 |
|
图 3 Ar*=0.1时阻尼与分形粗糙度的关系 |
|
图 4 D=1.4时阻尼与法向接触载荷的关系 |
|
图 5 D=1.6时阻尼与法向接触载荷的关系 |
|
图 6 G*=10-7, D较小时阻尼与法向接触载荷的关系 |

|
图 7 G*=10-7, D较大时阻尼与法向接触载荷的关系 |
1) 针对变化凸起[49-50]顶端曲率半径和连续法向载荷, 建立新的粗糙表面法向接触刚度与法向接触阻尼模型.
2) 法向接触阻尼随着表面粗糙轮廓分形维数的增加而先减小后增大.
3) 表面粗糙轮廓分形维数小于第一拐点时, 法向接触阻尼随着分形粗糙度的加大而加大; 表面粗糙轮廓分形维数大于第一拐点时, 法向接触阻尼随着分形粗糙度的增大而减小.
4) 法向接触阻尼随着法向接触载荷的增大而先减小后增加.
| [1] |
田红亮, 钟先友, 秦红玲, 等. 依据各向异性分形几何理论的固定结合部法向接触力学模型[J]. 机械工程学报, 2013, 49(21): 108-122. |
| [2] |
田红亮, 钟先友, 赵春华, 等. 区分弹性与塑性变形的结合面法向校正模型[J]. 机械工程学报, 2014, 50(17): 107-123. |
| [3] |
田红亮, 钟先友, 赵春华, 等. 计及弹塑性及硬度随表面深度变化的结合部单次加载模型[J]. 机械工程学报, 2015, 51(5): 90-104. |
| [4] |
田红亮, 赵春华, 朱大林, 等. 金属材料结合部法切向刚度修正与实验验证[J]. 农业机械学报, 2012, 43(6): 207-214. DOI:10.6041/j.issn.1000-1298.2012.06.037 |
| [5] |
田红亮, 朱大林, 秦红玲, 等. 结合部法向载荷解析解修正与定量实验验证[J]. 农业机械学报, 2011, 42(9): 213-218. |
| [6] |
田红亮, 赵春华, 朱大林, 等. 整个螺栓结合部的法向连接动刚度及试验验证[J]. 西安交通大学学报, 2012, 46(9): 31-36. |
| [7] |
田红亮, 朱大林, 秦红玲. 固定接触界面法向静弹性刚度[J]. 应用力学学报, 2011, 28(3): 318-322. |
| [8] |
田红亮, 赵春华, 方子帆, 等. 微动结合部的一次加载过程[J]. 振动与冲击, 2014, 33(13): 40-52. |
| [9] |
田红亮, 赵春华, 方子帆, 等. 基于各向异性分形理论的结合面切向刚度改进模型[J]. 农业机械学报, 2013, 44(3): 257-266. |
| [10] |
田红亮, 方子帆, 朱大林, 等. 固定接触界面切向静弹性刚度问题研究[J]. 应用力学学报, 2011, 28(5): 458-464. |
| [11] |
田红亮, 陈从平, 方子帆, 等. 应用改进分形几何理论的结合部切向刚度模型[J]. 西安交通大学学报, 2014, 48(7): 46-52. |
| [12] |
田红亮, 刘芙蓉, 方子帆, 等. 结合部静摩擦因数修正与定量实验验证[J]. 农业机械学报, 2013, 44(10): 282-293. DOI:10.6041/j.issn.1000-1298.2013.10.046 |
| [13] |
田红亮, 赵春华, 方子帆, 等. 金属材料表面静摩擦学特性的预测研究——理论模型[J]. 振动与冲击, 2013, 32(12): 40-44, 66. DOI:10.3969/j.issn.1000-3835.2013.12.008 |
| [14] |
田红亮, 刘芙蓉, 赵春华, 等. 金属材料表面静摩擦学特性的预测研究——实验佐证[J]. 振动与冲击, 2014, 33(1): 209-220. DOI:10.3969/j.issn.1000-3835.2014.01.036 |
| [15] |
田红亮, 赵春华, 方子帆, 等. 基于各向异性分形几何理论的摩擦非线性数学模型[J]. 振动与冲击, 2013, 32(23): 135-144. DOI:10.3969/j.issn.1000-3835.2013.23.025 |
| [16] |
田红亮, 赵春华, 方子帆, 等. 基于修正分形理论的结合面静摩擦模型[J]. 华中科技大学学报(自然科学版), 2013, 41(11): 71-75. |
| [17] |
田红亮, 朱大林, 秦红玲. 结合面静摩擦因数分形模型的建立与仿真[J]. 应用力学学报, 2011, 28(2): 158-162. |
| [18] |
田红亮, 刘芙蓉, 方子帆, 等. 引入各向同性虚拟材料的固定结合部模型[J]. 振动工程学报, 2013, 26(4): 561-573. DOI:10.3969/j.issn.1004-4523.2013.04.013 |
| [19] |
TIAN Hongliang, LI Bin, LIU Hongqi, et al. A new method of virtual material hypothesis-based dynamic modeling on fixed joint interface in machine tools[J]. Elsevier International Journal of Machine Tools & Manufacture, 2011, 51(3): 239-249. |
| [20] |
田红亮, 方子帆, 赵春华, 等. 依据修正GW理论的结合部法向接触研究[J]. 华中科技大学学报(自然科学版), 2014, 42(6): 38-42, 47. |
| [21] |
田红亮, 赵美云, 郑金华, 等. 新的柔性结合部法向接触刚度和接触阻尼方程[J]. 西安交通大学学报, 2015, 49(1): 118-126. |
| [22] |
田红亮, 郑金华, 赵春华, 等. 界面损耗因子与法向阻尼的计算方法[J]. 上海交通大学学报, 2015, 49(5): 687-694. |
| [23] |
尤晋闽, 陈天宁. 结合面法向动态参数的分形模型[J]. 西安交通大学学报, 2009, 43(9): 91-94. DOI:10.3321/j.issn:0253-987X.2009.09.020 |
| [24] |
田红亮, 方子帆, 朱大林. 赫兹点接触133年[J]. 三峡大学学报(自然科学版), 2014, 36(2): 88-97. |
| [25] |
田红亮, 郑金华, 方子帆, 等. 阻尼系统的特征[J]. 三峡大学学报(自然科学版), 2015, 37(2): 75-82. |
| [26] |
MAO Kuanmin, LI Bin, WU Jun, et al. Stiffness influential factors-based dynamic modeling and its parameter identification method of fixed joints in machine tools[J]. Elsevier International Journal of Machine Tools & Manufacture, 2010, 50(2): 156-164. |
| [27] |
MAO Kuanmin, ZHU Ming, XIAO Weiwei, et al. A method of using turning process excitation to determine dynamic cutting coefficients[J]. Elsevier International Journal of Machine Tools & Manufacture, 2014, 87: 49-60. |
| [28] |
XIAO Weiwei, MAO Kuanmin, ZHU Ming, et al. Modelling the spindle-holder taper joint in machine tools:a tapered zero-thickness finite element method[J]. Elsevier Journal of Sound and Vibration, 2014, 333(22): 5836-5850. DOI:10.1016/j.jsv.2014.06.023 |
| [29] |
LI Hongqi, LI Bin, MAO Kuanmin, et al. A parameterized model of bolted joints in machine tools[J]. International Journal of Acoustics and Vibration, 2014, 19(1): 10-20. |
| [30] |
LI Bin, CAI Hui, MAO Xinyong, et al. Estimation of CNC machine-tool dynamic parameters based on random cutting excitation through operational modal analysis[J]. Elsevier International Journal of Machine Tools & Manufacture, 2013, 71: 26-40. |
| [31] |
LI Bin, LUO Bo, MAO Xinyong, et al. A new approach to identifying the dynamic behavior of CNC machine tools with respect to different worktable feed speeds[J]. Elsevier International Journal of Machine Tools & Manufacture, 2013, 72: 73-84. |
| [32] |
MAO Xinyong, LUO Bo, LI Bin, et al. An approach for measuring the FRF of machine tool structure without knowing any input force[J]. Elsevier International Journal of Machine Tools & Manufacture, 2014, 86: 62-67. |
| [33] |
TAN Bo, MAO Xinyong, LIU Hongqi, et al. A thermal error model for large machine tools that considers environmental thermal hysteresis effects[J]. Elsevier International Journal of Machine Tools & Manufacture, 2014, 82/83: 11-20. |
| [34] |
LI Linwen, LI Bin, EHMANN K F, et al. A thermo-mechanical model of dry orthogonal cutting and its experimental validation through embedded micro-scale thin film thermocouple arrays in PCBN tooling[J]. Elsevier International Journal of Machine Tools & Manufacture, 2013, 70: 70-87. |
| [35] |
LI Linwen, LI Bin, LI Xiaochun, et al. Experimental investigation of hard turning mechanisms by PCBN tooling embedded micro thin film thermocouples[J]. Transactions of the ASME Journal of Manufacturing Science and Engineering, 2013, 135(4): 041012-1. DOI:10.1115/1.4023722 |
| [36] |
PENG Fangyu, MA J Y, WANG W, et al. Total differential methods based universal post processing algorithm considering geometric error for multi-axis NC machine tool[J]. Elsevier International Journal of Machine Tools & Manufacture, 2013, 70: 53-62. |
| [37] |
ZHANG S J, TO S, WANG H T. A theoretical and experimental investigation into five-DOF dynamic characteristics of an aerostatic bearing spindle in ultra-precision diamond turning[J]. Elsevier International Journal of Machine Tools & Manufacture, 2013, 71: 1-10. |
| [38] |
ZHANG S J, TO S. A theoretical and experimental investigation into multimode tool vibration with surface generation in ultra-precision diamond turning[J]. Elsevier International Journal of Machine Tools & Manufacture, 2013, 72: 32-36. |
| [39] |
ZHANG S J, TO S, CHEUNG C F, et al. Dynamic characteristics of an aerostatic bearing spindle and its influence on surface topography in ultra-precision diamond turning[J]. Elsevier International Journal of Machine Tools & Manufacture, 2012, 62: 1-12. |
| [40] |
ZHANG S J, TO S. A theoretical and experimental study of surface generation under spindle vibration in ultra-precision raster milling[J]. Elsevier International Journal of Machine Tools & Manufacture, 2013, 75: 36-45. |
| [41] |
ZHANG S J, TO S. The effects of spindle vibration on surface generation in ultra-precision raster milling[J]. Elsevier International Journal of Machine Tools & Manufacture, 2013, 71: 52-56. |
| [42] |
WANG Lei, LIU Haitao, ZHANG Jun, et al. Analysis and modeling for flexible joint interfaces under micro and macro scale[J]. Elsevier Precision Engineering, 2013, 37(4): 817-824. DOI:10.1016/j.precisioneng.2013.03.008 |
| [43] |
WANG Lei, LIU Haitao, YANG Lei, et al. The effect of axis coupling on machine tool dynamics determined by tool deviation[J]. Elsevier International Journal of Machine Tools & Manufacture, 2015, 88: 71-81. |
| [44] |
MI Liang, YIN Guofu, SUN Mingnan, et al. Effects of preloads on joints on dynamic stiffness of a whole machine tool structure[J]. Springer Journal of Mechanical Science and Technology, 2012, 26(2): 495-508. DOI:10.1007/s12206-011-1033-4 |
| [45] |
JIANG Shuyun, ZHENG Yunjian, ZHU Hua. A contact stiffness model of machined plane joint based on fractal theory[J]. Transactions of the ASME Journal of Tribology, 2010, 132(1): 011401-1. DOI:10.1115/1.4000305 |
| [46] |
JIANG Shuyun, MAO Hebing. Investigation of variable optimum preload for a machine tool spindle[J]. Elsevier International Journal of Machine Tools & Manufacture, 2010, 50(1): 19-28. |
| [47] |
XU Min, JIANG Shuyun, CAI Ying. An improved thermal model for machine tool bearings[J]. Elsevier International Journal of Machine Tools & Manufacture, 2007, 47(1): 53-62. |
| [48] |
ZHANG Xueliang, WANG Nanshan, LAN Guosheng, et al. Tangential damping and its dissipation factor models of joint interfaces based on fractal theory with simulations[J]. Transactions of the ASME Journal of Tribology, 2014, 136(1): 011704-1. |
| [49] |
丁玉坤. 钢筋混凝土墙板内置无粘结钢支撑抗冲切研究[J]. 哈尔滨工业大学学报, 2014, 46(8): 1-9. |
| [50] |
WANG Shengfei, FU Pengqiang, ZHANG Feihu, et al. Investigation of surface micro waviness in single point diamond fly cutting[J]. Journal of Harbin Institute of Technology (New Series), 2014, 21(5): 119-123. |
 2016, Vol. 48
2016, Vol. 48


