近年来,通过电解、激光等加工方式在摩擦副表面进行人工微造型的表面织构技术,由于能够有效改善摩擦副的润滑性能而越来越受到人们的关注[1-2].国内外学者亦开始探索将表面织构应用到滑动轴承,以改善其承载能力和润滑性能.通过试验手段研究表面织构对滑动轴承性能影响的首推Sinanoglu等[3-4]的工作,他们试验研究了轴颈开设的微织构对滑动轴承压力分布和承载能力的影响,试验结果表明, 合理的微织构可以提升滑动轴承的承载能力.其后更多的学者通过理论方法分析了表面织构对滑动轴承性能的影响. Nacer等[5-6]通过求解Reynolds方程分析了球形和圆柱形织构对滑动轴承性能的影响,发现微织构设计与轴承结构和工况参数关系密切,以及合理设计的微织构可以提升滑动轴承性能的事实. Kango等[7]在考虑非牛顿流体的条件下求解Reynolds方程,也获得了非牛顿流体润滑条件下,微织构能够提升滑动轴承承载能力和润滑性能的结果. Brizmer等[8]分析了球形织构的分布位置和尺寸对滑动轴承承载能力的影响,并以承载能力最大为目标对球形织构进行了结构优化. Ismail等[9]建立了考虑流体惯性效用的Reynolds方程,并以此为基础对三角形状和椭球形状微织构的滑动轴承性能进行了分析,指出微织构布置方式的差异影响微织构提升轴承承载能力和降低摩擦功耗的程度.林起崟等[10]以速度滑移边界表征微织构的作用,在二维尺度下分析了微织构位置和长度对滑动轴承摩擦阻力和承载能力的影响,同样发现微织构能够提升滑动轴承性能.齐烨等[11]采用基于N-S方程的CFD方法, 在二维尺度下分析了微织构分布位置对滑动轴承承载能力的影响,李以农等[12]也采用CFD方法分析了矩形织构的尺寸和位置对滑动轴承性能的影响,结果表明将微织构布置于轴承承载区有助于轴承承载能力的提升,以及存在一个使得轴承承载能力最大或摩擦系数最小的最优微织构分布密度.上述研究工作表明,在轴颈或轴瓦上合理地布置微织构可以提升滑动轴承的摩擦学性能,滑动轴承性能的提升程度与微织构的形状、分布位置、密度、尺寸以及滑动轴承的结构和工况参数等因素相关.目前, 国内外有关织构化滑动轴承特性的研究中,有些只是以单一结构类型的微织构为研究对象,有些则是基于Reynolds方程的数值分析,研究内容尚缺乏宏观系统性和通用普适性,研究结果的正确性亦因数学方程的简化尚有待考证.
本文针对矩形、圆柱形和三角形微织构结构,采用基于N-S方程CFD技术,建立了织构化径向滑动轴承的三维数值分析模型,并进行了数值仿真,较为系统地分析了微织构形状、分布位置、密度和尺寸对径向滑动轴承摩擦学性能的影响,以丰富和完善微织构对滑动轴承性能影响的认识和理解.
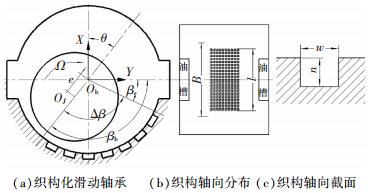
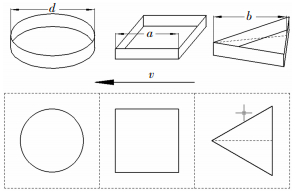
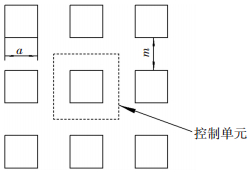
1 仿真模型及控制方程图 1为本文分析所涉及的滑动轴承和微织构的结构示意图.滑动轴承采用双侧供油,织构沿轴承圆周方向的分布位置由织构区起始角βa和终止角βb确定,Δβ为织构区包角;本文分析涉及的织构均沿轴承轴向方向对称分布,定义织构的周向分布长度l与轴瓦宽度B之比为织构轴向分布率,用以确定织构沿轴承轴向的分布位置;单个织构的尺寸则由其宽度w和深度n确定. 图 2为本文考虑的圆柱形、矩形和等边三角形3种典型织构形状,织构宽度w分别与3种织构形状下的直径d、边长a和高b相对应.某一确定位置处的织构密度由织构面积率s表征,织构面积率s指单个织构的周向截面面积占控制单元面积的比率,控制单元为相邻织构之间距中点围成的虚拟矩形(图 3中虚线),对于本文分析涉及的圆柱形、矩形和等边三角形织构,其织构面积率分别为πd2/m2、4a2/m2和2asb/m2(as为等边三角形织构的边长).
|
图 1 滑动轴承及微织构结构示意图 |
|
图 2 圆柱形、矩形等边三角形微织构结构示意图 |
|
图 3 织构面积率定义示意图 |
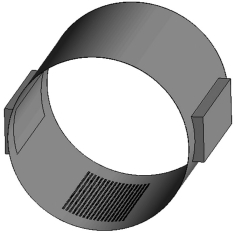
分析中,滑动轴承直径D=100 mm,宽径比B/D=1.0,间隙比Ψ=0.002,润滑油动力黏度μ=0.004 6 Pa·s、密度ρ=925.3 kg/m3.由于本文主要探讨表面织构对滑动轴承性能的影响,所以在整个分析中滑动轴承结构参数及润滑油物性参数不变.采用前处理软件Gambit进行织构化滑动轴承流体域建模及网格划分,单元形式为六面体单元,图 4给出了织构化滑动轴承流体域的三维模型.
|
图 4 织构化滑动轴承流体域的三维模型 |
将模型导入Fluent软件中进行仿真分析.分析中假设润滑油为不可压缩流体,不考虑流体与壁面间的热交换及润滑油的温黏特性;采用Schnerr-Sauer模型模拟流场的空化效应;采用Realizible k-ε模型模拟流场的湍流效应;模型内表面设置为旋转壁面,以模拟轴颈的旋转运动;外表面设置为固定壁面;模型端面设置为环境压力,进油口处设置为进油压力.
由于Reynolds方程忽略了流体的惯性力,低估了微织构的压力贡献[13-14],因此本文采用基于N-S方程的CFD方法对织构化径向滑动轴承进行性能分析,N-S方程的表达式为

|
式中: t为时间;u为流体速度;F为单位质量流体上的质量力;p为流体压强.
采用SIMPLE算法对压力/速度耦合进行求解,收敛精度为10-5.获得轴承油膜的压力、切应力和速度分布后,可由压力对面积的积分求得轴承的油膜承载力为

|
轴承油膜的摩擦力可由切应力对面积的积分求得:
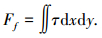
|
轴承油膜的摩擦因数即为摩擦力与承载力之比:
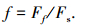
|
润滑油流量可由出口处速度对面积的积分求得:
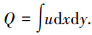
|
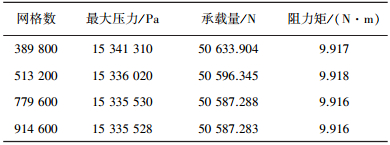
模型的网格质量和密度是保证计算结果准确性的关键,为了确定合理的单元网格数量,本文开展了多种单元网格数量的织构化滑动轴承性能计算.计算结果如表 1所示.由表 1可以看出, 当单元网格数目达到779 600后,计算结果的差异很小,因此本文后续计算中的网格数量均>779 600.
| 表 1 不同网格数量下滑动轴承特性计算结果 |
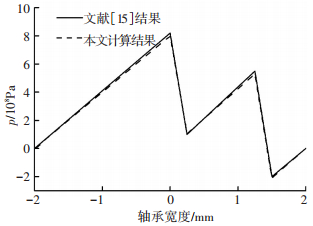
采用本文方法分别对文献[15]的两平板间二维织构、文献[16]的三维织构化滑块轴承和文献[17]的三维光滑滑动轴承进行计算,将计算结果与原文结果进行对比,结果如图 5、表 2、3所示.对比结果表明,采用本文方法计算出的结果与相关文献的结果基本吻合,表明了本文的织构化滑动轴承性能计算方法的正确性.
|
图 5 本文方法计算结果与文献[15]结果对比 |
| 表 2 本文方法计算结果与文献[16]结果对比 |
| 表 3 本文方法计算结果与文献[17]结果对比 |
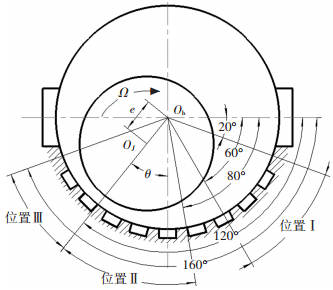
织构分布特征由织构周向分布位置和轴向分布率表征.织构周向分布位置由βa和βb确定(如图 6所示),织构轴向分布率σ为织构区轴向宽度l与轴承宽度B之比(即σ = l/B).
|
图 6 织构周向分布位置示意图 |
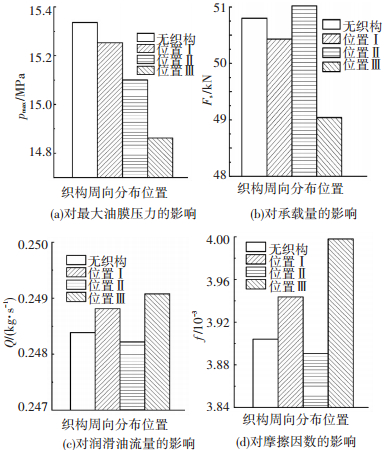
图 7给出了采用方形织构、偏心率ε=0.8、偏位角θ=30°、转速n=10 000 r/min、织构轴向分布率σ=0.60、织构面积率s=0.44时,织构周向分布位置对滑动轴承的最大油膜压力pmax、承载量Fs、润滑油流量Q及摩擦因数f的影响.从图 7可以看出,在滑动轴承轴瓦表面的任意位置布置微织构,最大油膜压力均有不同程度的降低,这是因为布置微织构后增加了油膜厚度所致;但对于微织构布置在主要承载区位置Ⅱ处的情况,虽然微织构降低了该位置处的最大油膜压力,但由于微织构产生的额外动压效应[14],总体上还是提升了滑动轴承的承载能力,由于该位置处的轴承承载力增加,但摩擦阻力变化不大,因此油膜的摩擦因数得以降低;另外,微织构的存在一方面增加了油膜厚度,从而造成流量的升高,但另一方面也降低了最大油膜压力,使得沿轴向方向的压力梯度减小,从而减小轴承端泄,织构这两种效应的综合作用导致了图 7所示的润滑油流量先降低后增加之趋势.
|
图 7 方形织构周向分布位置对滑动轴承性能的影响 |
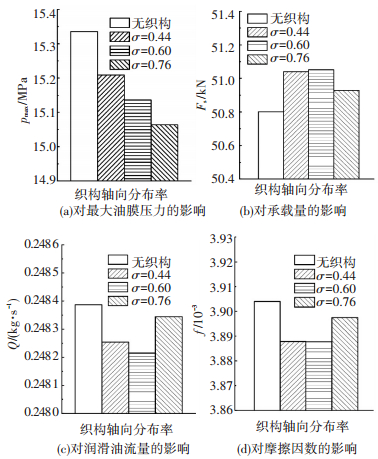
图 8给出了采用方形织构、偏心率ε=0.8、偏位角θ=30°、转速n=10 000 r/min、织构面积率s=0.44、微织构周向布置于位置Ⅱ处时,织构轴向分布率对滑动轴承性能的影响.从图 8可以看出,随着织构轴向分布率的增加,滑动轴承的承载能力呈先增大后减小的趋势,这是由于虽然微织构提供的额外动压效应能一定程度上提升轴承的承载能力,但当微织构的轴向分布率较小或过大时,微织构对承载力的提升程度不足以弥补其降低油膜压力所带来的负面作用,这表明存在一个最佳的织构轴向分布率,使得滑动轴承的承载能力最大;而流量呈现出的先增大后减小的趋势,亦是由织构具有增加油膜厚度和降低最大油膜压力的双重作用所导致的.
|
图 8 织构轴向分布率对滑动轴承性能的影响 |
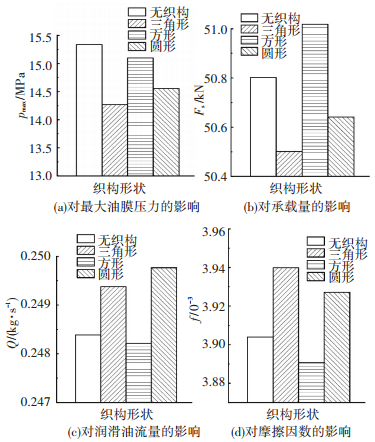
图 9给出了微织构周向布置于位置Ⅱ处、偏心率ε=0.8、偏位角θ=30°、转速n=10 000 r/min、织构轴向分布率σ=0.60、织构面积率s=0.44时,织构形状对滑动轴承性能的影响.从图 9可以看出,虽然3种织构都布置在承载区,但是对滑动轴承的性能影响却相去甚远,由于在本文结构和工况条件下,方形织构对轴承油膜压力的降低程度最小,因此只有方形织构提升了滑动轴承的承载能力.考虑到文献[6]曾经获得了圆形织构可提升滑动轴承承载能力的结果(织构分布位置、尺寸及工况参数均与本文不同),表明滑动轴承性能的提升有赖于微织构形状和分布的合理匹配.
|
图 9 织构形状对滑动轴承性能的影响 |
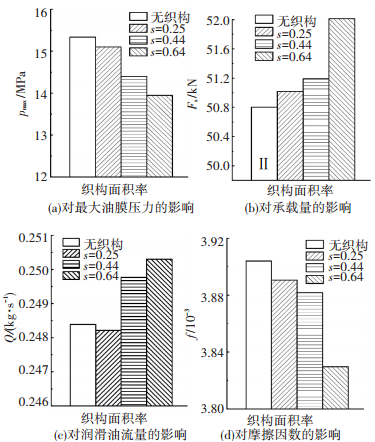
图 10给出了微织构周向布置于位置Ⅱ处,采用方形织构、偏心率ε=0.8、偏位角θ=30°、转速n=10 000 r/min、织构轴向分布率σ=0.60时,织构密度对滑动轴承性能的影响.从图 10可以看出,在织构面积率由0.25增加至0.64的过程中,织构对滑动轴承承载能力的提升效果逐渐增强,摩擦因数也逐渐降低,这表明在可提升滑动轴承性能的位置处,增大织构密度有助于提升滑动轴承性能,但织构密度的增加也会给加工带来困难,因此应根据实际情况确定合理的织构密度.
|
图 10 织构面积率对滑动轴承性能的影响 |
图 11给出了微织构周向布置于位置Ⅱ处,采用方形织构、偏心率ε=0.8、偏位角θ=30°、转速n=10 000 r/mi、织构轴向分布率σ=0.60时,织构宽度对滑动轴承性能的影响.从图 11可以看出,在织构宽度由0.5 mm增加至2 mm的过程中,滑动轴承的承载能力逐渐下降,摩擦因数先降低后增大.这表明滑动轴承在提升承载能力和降低摩擦功耗之间,存在着一个织构宽度的选择问题.

|
图 11 织构宽度对滑动轴承性能的影响 |
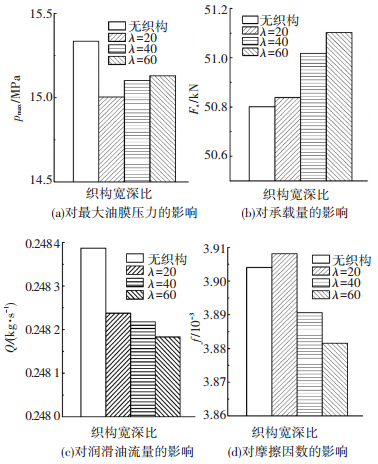
织构宽深比λ为织构宽度w与深度n之比. 图 12给出了在位置Ⅱ处,采用方形织构、偏心率ε=0.8、偏位角θ=30°、转速n=10 000 r/min、织构轴向分布率σ=0.60、织构面积率s=0.44时,织构宽深比对滑动轴承性能的影响.从图 12可以看出,在织构宽深比由20增加至60的过程中,滑动轴承的承载能力逐渐增强,摩擦因数逐渐降低.这表明适当增加微织构的宽度或减小其深度,可提升滑动轴承的性能,这与文献[5]所得结论是一致的.但有些文献的研究结果表明油膜承载能力随宽深比的增加呈现先增大后减小的趋势,即存在一个最优宽深比使得油膜承载能力最大[15].造成上述差异的原因是本文采用的织构形式、分布位置、尺寸及工况条件等均与其他文献不同,但作者对这些文献得出的结论表示认同.因为当织构宽深比很大时,即织构的宽度远大于其深度时,可将该轴承视为光滑滑动轴承,其承载能力必低于具有合理宽深比的织构化滑动轴承;而当织构宽深比很小时,即织构的宽度远小于其深度时,油膜厚度的急剧增加必将导致轴承承载能力的降低.
|
图 12 织构宽深比对滑动轴承性能的影响 |
1) 无论在滑动轴承瓦面上的任何位置布置微织构,均会降低滑动轴承的最大油膜压力,但当微织构布置于滑动轴承主要承载区时,可提高滑动轴承的承载能力, 降低其润滑油流量和摩擦因数.
2) 微织构形状对滑动轴承性能的影响差异较大,就本文的研究来看,方形微织构对滑动轴承承载能力的提升作用最大,但还是应当指出,滑动轴承性能的提升有赖于微织构形状和分布的合理匹配.
3) 当微织构布置于有利于提升滑动轴承性能的位置时,存在一个最优的织构轴向分布率、织构密度、织构宽度和织构宽深比,使得滑动轴承的承载能力最大, 摩擦因数最小.
| [1] |
钱双庆. 表面织构电解加工技术的基础研究与应用[D]. 南京: 南京航空航天大学, 2011.
|
| [2] |
ETSION I. State of the art in laser surface texturing[J]. Trans of the ASME, 2005, 127: 248-253. DOI:10.1115/1.1828070 |
| [3] |
SINANOGLU C, NAIR F, KARAMIS M B. Effects of shaft surface texture on journal bearing pressure distribution[J]. Journal of Materials Processing Technology, 2005, 168: 344-353. DOI:10.1016/j.jmatprotec.2005.02.252 |
| [4] |
SINANOGLU C. The analysis of the effects of surface texture on the capability of load carriage of journal bearings using neural network[J]. Industrial Lubrication and Tribology, 2005, 57(1): 28-40. DOI:10.1108/00368790510575969 |
| [5] |
NACER T I, MASPEYROT P, FILLON M, et al. Effects of surface texture on journal-bearing characteristics under steady-state operating conditions[J]. Proceedings of the Institution of Mechanical Engineers Part J:Journal of Engineering Tribology, 2007, 221: 623-633. DOI:10.1243/13506501JET287 |
| [6] |
NACER T I, FILLON M, MASPEYROT P. Effect of textured area on the performances of a hydrodynamic journal bearing[J]. Tribology International, 2011, 44: 211-219. DOI:10.1016/j.triboint.2010.10.003 |
| [7] |
KANGO S, SHARMA R K. Studies on the influence of surface texture on the performance of hydrodynamic journal bearing using power law model[J]. Int J Surface Science and Engineering, 2010, 4(4/5/6): 505-524. DOI:10.1504/IJSURFSE.2010.035150 |
| [8] |
BRIZMER V, KLIGERMAN Y. A laser surface textured journal bearing[J]. Transactions of the ASME, 2012, 134: 1-9. |
| [9] |
ISMAIL S, SARANGI M. Hydrodynamic lubrication with deterministic micro textures consideringfluid inertia effect[J]. Tribology International, 2014, 69: 30-38. DOI:10.1016/j.triboint.2013.08.011 |
| [10] |
林起崟, 魏正英, 王宁, 等. 织构滑移表面对滑块轴承摩擦学性能的影响[J]. 华南理工大学学报(自然科学版), 2013, 41(3): 101-107. DOI:10.3969/j.issn.1000-565X.2013.03.015 |
| [11] |
齐烨, 常秋英, 李慧婷, 等. 织构化径向轴承的承载性能研究[J]. 润滑与密封, 2012, 37(12): 36-42. DOI:10.3969/j.issn.0254-0150.2012.12.009 |
| [12] |
李以农, 秦洁, 孟凡明. 微造型对滑动轴承摩擦学性能影响的研究[J]. 四川大学学报(工程科学版), 2012, 44(3): 229-234. |
| [13] |
ARGHIR M, ROUCON N, HELENCE M, et al. Theoretical analysis of the incompressible laminar flow in a macro-roughness cell[J]. Journal of Tribology, 2003, 125(4): 309-318. |
| [14] |
SAHIN F, GLAVATSKIH S B, ALMQVIST T, et al. Two-dimensional CFD analysis of micro-patterned surface in hydrodynamic lubrication[J]. Journal of Tribology, 2005, 127(1): 96-102. DOI:10.1115/1.1828067 |
| [15] |
RAHMANI R, SHIRVANI A, SHIRVANI H. Optimization of partially textured parallel thrust bearings with square-shaped micro-dimples[J]. Tribology Transactions, 2007, 50(3): 401-406. DOI:10.1080/10402000701429261 |
| [16] |
BRAJDIC M P, GOSMAN A D, IOANNIDES E, et al. CFD analysis of a low friction pocketed pad bearing[J]. Journal of Tribology, 2005, 127(4): 803-812. DOI:10.1115/1.2032990 |
| [17] |
VINCENT B, MASPEYROT P, FRENE J. Starvation and cavitation effects in finite grooved journal bearing[J]. Tribology Series, 1995, 30: 455-464. DOI:10.1016/S0167-8922(08)70651-5 |
 2016, Vol. 48
2016, Vol. 48