为了快速、准确地从海量图像数据中检索出需要的图像,基于内容的图像检索快速发展,成为模式识别和计算机视觉领域的研究热点.图像内容包括纹理、颜色、形状等信息.相对于纹理、颜色等基本特征,形状是高级别的视觉信息[1],更具视觉表征性[2],更能从语义上描述目标图像的内容[3],是基于内容图像检索的关键.
现有形状描述方法主要包括基于轮廓边界点集和基于骨架的两类方法.基于轮廓边界点集的形状描述法主要有形状上下文描述法(Shape context)[4]、内距离形状上下文描述法IDSC(inner-distance shape context)[5]、惯性轴描述法(Axis of Least Inertia)[6-7]、带符号的三角形面积形状描述法TAR(triangle area representation)[8-9]和基于变换域的形状描述法[3, 10-12]等.形状上下文描述法通过直方图记录轮廓序列上某个点与其他所有点的空间分布关系,具有较强的形状描述能力[4].内距离形状上下文描述法通过轮廓点之间的内距离代替形状上下文描述法中的欧氏距离,更有效地表征形状的局部信息[5].惯性轴描述法以最小惯性轴为参考线提取形状的特征向量,可同时描述形状的轮廓和区域信息,具有描述多层次复杂形状的能力[6-7].三角形面积描述法在所有尺度级别上通过带符号的三角形面积,表示形状中每个点的凹凸性,可以同时描述形状的局部与全局特征[8-9].基于变换域的形状描述法主要有多级弦长函数的傅里叶形状描述子MCLFD(Fourier shape descriptor based on multi-level chord length function)[10]、多尺度拱高形状描述MSAH(multi-scale arch height shape description)[11]和HSC (hierarchical string cuts)[12]等,这些方法均描述了形状的全局特征和细节信息.基于骨架的形状检索方法通过提取形状的骨架,准确描述形状的几何特征和拓扑结构,具有较高的形状匹配精度[13-14].
在现有形状描述方法的基础上,为进一步提高形状的识别精度,本文提出应用全方向形状特征码的图像检索方法.本方法在特定方向上利用一组等距分割线将形状分成若干分割份,计算所有分割份中每个点的带符号三角形面积和每个分割份的形状复杂度SC(shape complex),得到形状特定方向上的特征码.旋转该组分割线,计算形状每个分割方向上的特征码,得到形状的全方向特征码.计算待匹配形状的主方向,确定两个待匹配形状的对应方向,计算两个待匹配形状的相似度.全方向形状特征码描述法进一步将形状的全局特征和局部特征融合,具有平移、尺度、旋转不变性,对形状的形变具有一定的鲁棒性,具有更高的形状识别精度.
1 形状特征码 1.1 形状复杂度带符号的三角形面积形状描述同时包含了形状的局部与全局特征,具有平移、旋转和缩放不变性,且有较强的抗噪声和扭曲能力[8-9].设形状由N个轮廓点组成,任意3个连续轮廓点(xn-t, yn-t)、(xn, yn)、(xn+t, yn+t)构成的带符号三角形面积STAR为
| $ {S_{{\rm{TAR}}}}\left( {n,t} \right) = \frac{1}{2}\left| {\begin{array}{*{20}{c}} {{x_{n - t}}}&{{y_{n - t}}}&1\\ {{x_n}}&{{y_n}}&1\\ {{x_{n + t}}}&{{y_{n + t}}}&1 \end{array}} \right|, $ | (1) |
式中n∈[1, N]、t∈[1,
通过所有轮廓点各尺度级别的最大STAR值和最小STAR值,度量形状轮廓的复杂度,形状复杂度SC公式为
| $ {\text{SC = }}\frac{1}{N}\sum\limits_{n = 1}^N {\left| {\frac{{\mathop {\max }\limits_{1 \leqslant t \leqslant \lfloor\left( {N - 1} \right)/2} {S_{{\text{TAR}}}}\left( {n,t} \right) - \mathop {\max }\limits_{1 \leqslant t \leqslant \lfloor\left( {N - 1} \right)/2} {S_{{\text{TAR}}}}\left( {n,t} \right)}}{{\mathop {\max }\limits_{1 \leqslant t \leqslant \lfloor\left( {N - 1} \right)/2} {S_{{\text{TAR}}}}\left( {n,t} \right)}}} \right|} . $ | (2) |
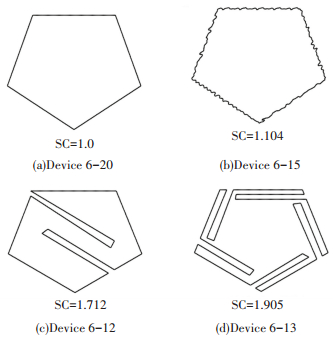
如图 1所示,从人类视觉的感知角度,图 1(a)、(b)、(c)、(d)这4个形状越来越复杂,形状复杂度SC也逐渐增大. 图 1(a)、(b)相似度较高,形状复杂度相近;图 1(c)、(d)相似度较高,形状复杂度相近.
|
图 1 形状复杂度SC示例 Figure 1 Examples of the shape complexity |
规定某一方向为初始方向Odir(0),求出与初始方向平行且与形状轮廓最外侧相交的两条边界线,如图 2中规定0度方向为初始方向,两条实线为边界线.利用与初始方向平行的n条直线将两条边界线之间的部分平均分割为n+1等份,如图 2中8条虚线将边界线之间的部分平均分割为9等份.利用式(1)计算形状每个分割份中每个点的STAR值,利用式(2)计算形状n+1个分割份的形状复杂度SC,则形状初始方向Odir(0)上的特征码FC(Odir(0))为
| $ \left\{ \begin{array}{l} {\rm{FC}}\left( {{O_{{\rm{dir}}}}\left( 0 \right)} \right) = \left\{ {\overline {{\rm{SC}}} \left( {1,{O_{{\rm{dir}}}}\left( 0 \right)} \right),\overline {{\rm{SC}}} \left( {2,{O_{{\rm{dir}}}}\left( 0 \right)} \right), \cdots ,} \right.\\ \left. {\;\;\;\;\;\;\;\;\;\;\;\;\;\overline {{\rm{SC}}} \left( {j,{O_{{\rm{dir}}}}\left( 0 \right)} \right), \cdots ,\overline {{\rm{SC}}} \left( {n + 1,{O_{{\rm{dir}}}}\left( 0 \right)} \right)} \right\},\\ \overline {{\rm{SC}}} \left( {j,{O_{{\rm{dir}}}}\left( 0 \right)} \right) = \frac{{{\rm{SC}}\left( {j,{O_{{\rm{dir}}}}\left( 0 \right)} \right)}}{{\sum\limits_{x = 1}^{n + 1} {{\rm{SC}}\left( {x,{O_{{\rm{dir}}}}\left( 0 \right)} \right)} }}. \end{array} \right. $ |

|
图 2 初始方向形状分割示意图 Figure 2 Diagram of the shape segmentation in the original direction |
|
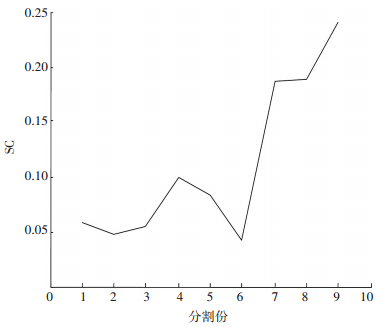
图 3 形状初始方向特征码示意图 Figure 3 Diagram of the shape feature code in the original direction |
从初始方向Odir(0)开始,每次间隔特定角度dangle对形状进行分割,计算形状特定方向Odir(i)上的特征码FC(Odir(i)),直到旋转回初始方向为止,共有m=360/dangle分割方向.间隔角度dangle必须能被360整除,当间隔角度dangle为1时,分割方向m值最大为360.形状特定方向Odir(i)的特征码FC(Odir(i))为
| $ \left\{ \begin{array}{l} {\rm{FC}}\left( {{O_{{\rm{dir}}}}\left( i \right)} \right) = \left\{ {\overline {{\rm{SC}}} \left( {1,{O_{{\rm{dir}}}}\left( i \right)} \right),\overline {{\rm{SC}}} \left( {2,{O_{{\rm{dir}}}}\left( i \right)} \right), \cdots ,} \right.\\ \left. {\;\;\;\;\;\;\;\;\;\;\;\;\;\overline {{\rm{SC}}} \left( {j,{O_{{\rm{dir}}}}\left( i \right)} \right), \cdots ,\overline {{\rm{SC}}} \left( {n + 1,{O_{{\rm{dir}}}}\left( i \right)} \right)} \right\},\\ \overline {{\rm{SC}}} \left( {j,{O_{{\rm{dir}}}}\left( i \right)} \right) = \frac{{{\rm{SC}}\left( {j,{O_{{\rm{dir}}}}\left( i \right)} \right)}}{{\sum\limits_{x = 1}^{n + 1} {{\rm{SC}}\left( {x,{O_{{\rm{dir}}}}\left( i \right)} \right)} }},\\ {O_{{\rm{dir}}}}\left( i \right) = {O_{{\rm{dir}}}}\left( 0 \right) + i \times {d_{{\rm{angle}}}},0 \le i < m. \end{array} \right. $ |
m个分割方向的特征码共同构成形状的全方向特征码FC:
| $ \left\{ \begin{array}{l} {\rm{FC}} = \left\{ {{\rm{FC}}\left( {{O_{{\rm{dir}}}}\left( 0 \right)} \right),{\rm{FC}}\left( {{O_{{\rm{dir}}}}\left( 1 \right)} \right), \cdots ,{\rm{FC}}\left( {{O_{{\rm{dir}}}}\left( i \right)} \right),} \right.\\ \left. {\;\;\;\;\;\;\;\;\;\;\;\; \cdots ,{\rm{FC}}\left( {{O_{{\rm{dir}}}}\left( {m - 1} \right)} \right)} \right\},\\ {O_{{\rm{dir}}}}\left( i \right) = {O_{{\rm{dir}}}}\left( 0 \right) + i \times {d_{{\rm{angle}}}},0 \le i < m. \end{array} \right. $ |
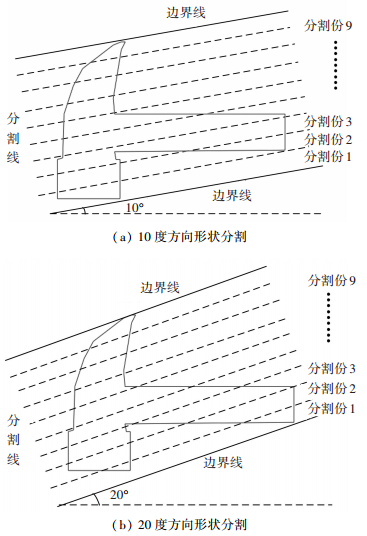
图 4为图 2从初始方向0度开始,每次间隔1度,10度和20度方向分割示意图,图 5为图 2形状全方向特征码的三维示意图.
|
图 4 形状分割示意图 Figure 4 Diagram of the shape segmentation |

|
图 5 形状全方向特征码三维示意图 Figure 5 Three-dimensional diagram of the omnidirectional shape feature code |
进行形状相似性匹配时,待匹配形状A和B可能发生过旋转,导致各分割方向不对应.为了确定对应的分割方向,需计算形状A、B各自的最小惯性轴,该轴不随形状转换而改变,唯一保存了形状的主方向.形状主方向位于通过形状重心且倾角为θ的直线上,倾角θ公式为[15]
| $ \theta = \frac{1}{2}{\rm{arctan}}\frac{{2{u_{11}}}}{{{u_{20}} - {u_{02}}}}. $ |
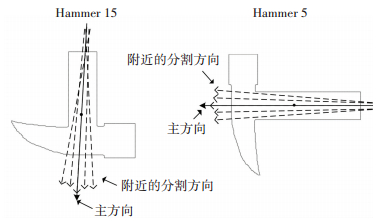
式中u11, u02, u20为形状的p+q阶中心矩. 图 6中Hammer15、Hammer5的主方向为带箭头的实线所示.
|
图 6 形状主方向 Figure 6 Shape main direction |
主方向可能会因形状的不均匀形变,产生一定的改变,导致两个待匹配形状对应方向的确定出现误差.为了准确确定形状A、B的对应方向,以形状A、B的主方向为参考,计算两个形状主方向附近分割方向的特征码差异,将特征码差异最小的两个分割方向作为形状A、B的对应方向,图 6中带箭头的虚线表示主方向附近的分割方向.设形状A的某一分割方向为Odir(a),形状B的某一分割方向为Odir(b),则形状A、B的分割方向Odir(a)、Odir(b)的特征码FCA(Odir(a))、FCB(Odir(b))差异度为
| $ D = \frac{1}{{n + 1}}\sum\limits_{x = 1}^{n + 1} {\left| {\overline {{\rm{SC}}} \left( {x,{O_{{\rm{dir}}}}\left( a \right)} \right) - \overline {{\rm{SC}}} \left( {x,{O_{{\rm{dir}}}}\left( b \right)} \right)} \right|} . $ | (3) |
设形状A、B的对应方向为Odir(a)、Odir(b),从对应方向开始,通过式(3)计算形状A、B各分割方向的特征码差异度,得到{D0, D1, …, Dm-1},形状A、B全方向特征码差异度为
| $ \begin{array}{l} {D_{{\rm{all}}}} = \frac{1}{m}\sum\limits_{i = 0}^{m - 1} {{D_i}} ,\\ m = 360/{d_{{\rm{angle}}}}. \end{array} $ |
式中,间隔角度dangle必须能被360整除.
形状A、B的形状相似度S为
| $ S = 1 - {D_{{\rm{all}}}}. $ |
全方向形状特征码满足尺度、旋转、平移不变性.全方向形状特征码使用每个方向所有分割份形状复杂度SC的和,对每个分割份的形状复杂度SC进行归一化,满足尺度不变性.全方向形状特征码是利用各分割方向对形状进行分割,形状复杂度SC是计算带符号的三角形面积STAR,均与形状特征点的绝对位置无关,不会因形状的平移产生变化,满足平移不变性.全方向形状特征码利用形状最小惯性轴保存的形状主方向,确定两个待匹配形状的对应方向,满足旋转不变性.
全方向形状特征码结合了三角形面积描述法[8]和惯性轴描述法[6],并通过全方向的形状分割,进一步将形状的局部与全局特征融合,对发生了形变和扭曲的形状具有更强的识别能力.
2 复杂性分析全方向形状特征码图像检索方法的时间复杂度分为全方向特征码计算时间复杂度和形状匹配时间复杂度两部分.设共有分割方向m个,形状特征点N个,每个分割方向下分割线n条,主方向附近分割方向的搜索范围为w.
全方向特征码的计算包含各分割方向的带符号三角形面积STAR和形状复杂度SC的计算.在某一分割方向下,n条分割线将形状分为n+1份.当分割线数目n为0,即形状没有被分割时,带符号三角形面积STAR的计算时间复杂度最大为O(N2),形状复杂度SC的计算时间复杂度为O(N),则单一分割方向下,形状特征码的最大计算时间复杂度为O(N2).全方向形状特征码的最大计算时间复杂度为O(m*N2),分割方向数m的最大值为360,则全方向形状特征码的最大计算时间复杂度为O(N2).
形状匹配包括主方向的计算、两个待匹配对象对应分割方向的计算和全方向特征码差异度的计算.主方向的计算时间复杂度为O(N)[15].两个待匹配对象的对应分割方向的计算时间复杂度为O(w2*(n+1)),w最大取值为10.全方向特征码差异度的计算时间复杂度为O(m*(n+1)),分割方向数m的最大值为360.形状匹配的时间复杂度为O(N+(n+1)(m+w2)),w最大取值为10,分割方向数m的最大值为360,分割线数目n通常为9,形状匹配阶段的时间复杂度较低,小于IDSC[5]、TAR[8]等的匹配时间复杂度.
3 实验结果和分析为评估本文提出的全方向形状特征码图像检索方法的检索性能,使用两个图像数据库进行测试.一个图像数据库是被广泛用来测试形状检索性能的标准测试集MPEG-7 CE-1 Part B,该数据库包含按语义分类的70类形状,每类20个,共1 400个形状图像.另一个图像数据库是本文通过真实建筑形状构建的数据集,该数据库从真实地图中选取70个形状各异的建筑物,如图 7中上方图所示.对每一个建筑物分别缩放0.49、0.7、1.37倍,得到3个建筑物,如图 7中下方图第一行从左至右依次是原始建筑、缩放0.49倍建筑、缩放0.7倍建筑、缩放1.37倍建筑.对原始建筑和3个缩放建筑分别旋转45°、135°、225°得到12个建筑,如图 7中下方图第二行、第三行、第四行的建筑分别为第一行建筑旋转45°、135°、225°.对原始建筑进行四种仿射变换,得到4个建筑,如图 7中下方图第五行所示.对每个建筑共进行了19次变换,得到了19个建筑,加上原始建筑,构成了一类相似建筑的20种形变. 70个原始建筑共形成了70类,每类20个相似建筑,共1 400个建筑的形状数据集.

|
图 7 真实建筑形状数据集 Figure 7 Shape data set of the actual structure |
性能评估使用通用的Bulls-eye测试方法[12],该方法对形状数据集中的每个形状均进行一次检索,共进行1 400次检索实验.在每次实验检索出的前40个相似性最高的形状中,计算检索形状的同类相似形状个数,并统计1 400次检索实验相似形状的总和.因一类相似形状有20个,共1 400次实验,相似形状总和最大为20*1400=28 000.统计得到的相似形状总和除以28 000为Bulls-eye测试的检索率.形状检索的时间是待检索形状和数据集中1 400个形状的特征匹配时间. MSAH[11]、MCLFD[10]、HSC[12]、IDSC[5]、TAR[8]与本文全方向形状特征码描述法在真实建筑形状数据集上的检索率和平均检索时间如表 1所示,在MPEG-7 CE-1 Part B形状数据集上的检索率和平均检索时间如表 2所示.
| 表 1 真实建筑形状数据集检索率 Table 1 Retrieval accuracy of the actual shape data set |
| 表 2 MPEG-7形状数据集检索率 Table 2 Retrieval accuracy of the MPEG-7 shape data set |
从表 1可以看出,在真实建筑形状数据集中本文全方向形状特征码描述法的检索率高于其他5个形状描述法.全方向形状特征码描述法可以准确识别真实建筑形状数据集中所有经过放大、缩小和旋转的形状,具有平移、旋转和尺度不变性,对因仿射变换造成的形状形变具有一定的鲁棒性.但较大程度的仿射变换导致建筑形变较大,造成误匹配和漏匹配,影响本文形状描述法的检索率.全方向形状特征码描述法的平均检索时间大于MSAH[11]、MCLFD[10]和HSC[12],主要是因为本文形状描述方法为了提高检索准确率,利用的形状特征较多,导致检索时间增加.
从表 2可以看出,在MPEG-7 CE-1 Part B形状数据集中本文全方向形状特征码描述法的检索率高于其他5个形状描述法,具有更强的形状描述能力,对发生了形变的形状具有更强的识别能力.在检索率大于80%的形状描述法中,本文全方向形状特征码描述法的平均检索时间小于TAR[8]、IDSC[5]的平均检索时间,仅大于HSC[12]的平均检索时间.在保证检索准确率的情况下,本文形状描述法具有较高的检索效率. 图 8给出了本文全方向形状特征码描述法在MPEG-7 CE-1 Part B形状数据集上的部分检索结果. 图 8中第1列为待检索形状,第2列到第8列为从MPEG-7数据集中检索出的与待检索形状相似度最高的7个形状,其中误匹配被用圆圈标出.从图 8中可以看出,误匹配形状与待检索形状还是存在一定程度相似性的,仅通过形状特征的识别,MPEG-7 CE-1 Part B形状数据集的检索率不可能达到100%[8].

|
图 8 全方向形状特征码描述法部分检索结果示例 Figure 8 Part of search results of the omnidirectional shape feature code method |
本文提出的全方向形状特征码图像检索方法通过全方向的形状分割和形状复杂度概念,度量形状各方向各部分的复杂度,进一步将形状的局部与全局特征融合.通过真实建筑形状数据集和MPEG-7 CE-1 Part B形状数据集的检索实验,表明本方法具有较高的形状检索准确率,具有平移、尺度、旋转不变性,对发生了形变和扭曲的形状具有较强的识别能力.
| [1] |
周瑜, 刘俊涛, 白翔. 形状匹配方法研究与展望[J].
自动化学报,2012, 38 (6) : 889-910.
ZHOU Yu, LIU Juntao, BAI Xiang. Research and perspective on shape matching[J]. Acta Automatica Sinica,2012, 38 (6) : 889-910. DOI: 10.3724/SP.J.1004.2012.00889 |
| [2] | EL-GHAZAL A, BASIR O, BELKASIM S. Invariant curvature-based Fourier shape descriptors[J]. Journal of Visual Communication and image Representation,2012, 23 (4) : 622-633. DOI: 10.1016/j.jvcir.2012.01.011 |
| [3] |
王斌. 一种不变的基于傅里叶变换的区域形状描述子[J].
电子学报,2012, 40 (1) : 84-88.
WANG Bin. An invariant region-shape descriptor based on fourier transform[J]. Acta Electronica Sinica,2012, 40 (1) : 84-88. DOI: 10.3969/j.issn.0372-2112.2012.01.014 |
| [4] | MORI G, BELONGIE S, MALIK J. Efficient shape matching using shape contexts[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2005, 27 (11) : 1832-1837. DOI: 10.1109/TPAMI.2005.220 |
| [5] | LING H B, JACOBS D W. Shape classification using the inner-distance[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2007, 29 (2) : 286-299. DOI: 10.1109/TPAMI.2007.41 |
| [6] | GURU D S, NAGENDRASWAMY H S. Symbolic representation of two-dimensional shapes[J]. Pattern Recognition Letters,2007, 28 (7) : 144-155. DOI: 10.1016/j.patrec.2006.06.017 |
| [7] |
李宗民, 陆天波, 桑鑫焱, 等. 基于最小惯性轴及链码的图像形状描述方法[J].
通信学报,2009, 30 (4) : 1-5.
LI Zongmin, LU Tianbo, SANG Xinyan, et al. Shape description based on axis of least inertia and chain[J]. Journal on Communications,2009, 30 (4) : 1-5. |
| [8] | ALAJLAN N, EL RUBE I, KAMEL M S, et al. Shape retrieval using triangle-area representation and dynamic space warping[J]. Pattern Recognition,2007, 40 (7) : 1911-1920. DOI: 10.1016/j.patcog.2006.12.005 |
| [9] | ALAJLAN N, KAMEL M S, FREEMAN G. Geometry-based image retrieval in binary image databases[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2008, 30 (6) : 1003-1013. DOI: 10.1109/TPAMI.2008.37 |
| [10] |
王斌. 一种基于多级弦长函数的傅里叶形状描述子[J].
计算机学报,2010, 33 (12) : 2387-2396.
WANG Bin. A fourier shape descriptor based on multi-level chord length function[J]. Chinese Journal of Computers,2010, 33 (12) : 2387-2396. DOI: 10.3724/SP.J.1016.2010.02387 |
| [11] |
王斌. 一种基于多尺度拱高形状描述的图像检索方法[J].
电子学报,2013, 41 (9) : 1821-1825.
WANG Bin. Image retrieval using multi-scale arch height shape description[J]. Acta Electronica Sinica,2013, 41 (9) : 1821-1825. DOI: 10.3969/j.issn.0372-2112.2013.09.024 |
| [12] | WANG B, GAO Y. Hierarchical string cuts: a translation, rotation, scale, and mirror invariant descriptor for fast shape retrieval[J]. IEEE Transactions on Image Processing,2014, 23 (9) : 4101-4111. DOI: 10.1109/TIP.2014.2343457 |
| [13] | BAI X, LATECKI L J. Path similarity skeleton graph matching[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2008, 30 (7) : 1282-1292. DOI: 10.1109/TPAMI.2007.70769 |
| [14] | ERDEM A, TARI S. A similarity-based approach for shape classification using Aslan skeletons[J]. Pattern Recognition Letters,2010, 31 (13) : 2024-2032. DOI: 10.1016/j.patrec.2010.06.003 |
| [15] | ZUNIC J, ROSIN P L, KOPANJA L. On the orientability of shapes[J]. IEEE Transactions on Image Processing,2006, 15 (11) : 3478-3487. DOI: 10.1109/TIP.2006.877527 |
 2016, Vol. 48
2016, Vol. 48


