无线传感器网络WSNs(wireless sensor networks)是由大量具有感知、处理以及路由功能的节点构成的网络系统[1].尽管与传统网络节点相比而言,传感器节点的处理能力、存储容量受到限制,但是它所具有的小体积、低成本使其应用范围相当广泛[2].具体来说,传感器可以以密集铺设方式组成网络系统用于环境监测、军事监测、医疗护理、濒危物种的跟踪以及灾后安全救援等[1-3].大多数的传感器节点采用电池供能,并且在网络部署完毕之后一般不可能或难以给节点再充电或者补充能量[4-6].而当网络中存在节点能量耗尽时,将会造成网络的分区或隔离,监测数据无法传输至sink节点,这对于以数据为中心的WSNs意味着网络生命的终结.因此,如何减少节点的能量消耗对于传感器网络而言至关重要.
一般而言,传感器节点的能耗主要在于数据感知、数据处理以及数据通信等方面,其中通信模块所消耗的能量是最主要的[4].此外,由于传感器网络数据多采用多跳传输,因而会使得sink周围节点能量负载明显大于其他节点,这就造成了能量不均衡问题,即“热点问题”[2,7-8]或“sink邻居问题”[5-7].因此,节约通信能耗以及尽可能使各个节点能耗均匀是延长网络生命期的主要方法.近年来,围绕着节约能耗以及能量均衡问题出现了一系列研究成果[2-15].为缓解“sink邻居问题”,可以利用WSN中的节点的移动性[2-10].利用移动代理[12-14]或令移动sink节点[3-10]周期性地沿着某一确定的或随机轨迹运动.这样,利用移动代理或sink节点位置的变换来实现能量均衡.文献[13]首次提出采用移动代理将多跳传输变为单跳传输.这种方法虽然可以有效地减少能量的消耗,但这是以增加时延为代价的,显然对于实时性应用不太合适.文献[5-6, 8, 11]将移动sink问题抽象成线性规划问题,以每个节点的初始能量以及流量保护作为限制条件,谋求网络生命期最大化.文献[12]则是以最小化网络的最大能量消耗,并且也假设sink在固定的站点停留,然后以节点初始能量以及逗留时间等作为限制条件.这种思路有个不足,在sink到达每一站停留时间的长短要考虑整个网络拓扑,因而计算较为复杂;同时sink节点每次逗留都以泛洪的方式将自身的位置信息通知各个节点,无形之中也增加了节点的能量消耗.
一般而言,传感器节点的能耗主要在于数据感知、数据处理以及数据通信等方面,其中通信模块所消耗的能量是最主要的[4].此外,由于传感器网络数据多采用多跳传输,因而会使得sink周围节点能量负载明显大于其他节点,这就造成了能量不均衡问题,即“热点问题”[2,7-8]或“sink邻居问题”[5-7].因此,节约通信能耗以及尽可能使各个节点能耗均匀是延长网络生命期的主要方法.近年来,围绕着节约能耗以及能量均衡问题出现了一系列研究成果[2-15].为缓解“sink邻居问题”,可以利用WSN中的节点的移动性[2-10].利用移动代理[12-14]或令移动sink节点[3-10]周期性地沿着某一确定的或随机轨迹运动.这样,利用移动代理或sink节点位置的变换来实现能量均衡.文献[13]首次提出采用移动代理将多跳传输变为单跳传输.这种方法虽然可以有效地减少能量的消耗,但这是以增加时延为代价的,显然对于实时性应用不太合适.文献[5-6, 8, 11]将移动sink问题抽象成线性规划问题,以每个节点的初始能量以及流量保护作为限制条件,谋求网络生命期最大化.文献[12]则是以最小化网络的最大能量消耗,并且也假设sink在固定的站点停留,然后以节点初始能量以及逗留时间等作为限制条件.这种思路有个不足,在sink到达每一站停留时间的长短要考虑整个网络拓扑,因而计算较为复杂;同时sink节点每次逗留都以泛洪的方式将自身的位置信息通知各个节点,无形之中也增加了节点的能量消耗.
本文提出静态sink与移动sink相结合的策略ESCMS,即静态sink位于网络中心,收集监控中心位置的数据,移动sink围绕静态sink节点一定半径做快速运动,并且在固定位置停留,收集一定范围内节点的数据.由于移动sink运动速度快,以及静态sink节点的存在,可减少单纯采用动态sink所带来的网络时延,从而增加了sink节点的吞吐量.同时,也能避免单纯使用静态sink所带来的“热点问题”.相比于文献[4, 10, 12]采用的多移动sink节能策略,本文所采用的静态与移动sink相结合的策略(ESCMS)可以减少sink移动控制的复杂性.
1 能耗模型及相关假设 1.1 能耗模型本文采用文献[2, 4-5, 14]所采用的一阶无线电模型来描述传感器节点的传输功耗:
| $ {{e}_{\text{rx}}}={{E}_{\text{elec}}}, $ |
| $ {{e}_{\text{tx}}}={{E}_{\text{elec}}}+{{\varepsilon }_{\text{amp}}}{{d}^{\alpha }}. $ |
式中:erx和etx分别表示节点接收、发送单位bit数据所消耗的能量,Eelec表示发送与接收电路发送或接收单位bit数据所消耗的能量,εamp表示放大电路能耗, d表示传输距离,α代表衰减系数.一般而言,α取值可在2~4之间,本文控制节点传输半径不大于87 m[9],使其为2.
1.2 相关假设1) 所有传感器节点均静止,并且具有相同的初始能量,并将初始能量记为Einitial.
2) 传感器节点采用固定的传输半径R,且所有传感器节点均匀独立地分布在半径为l=3R(0 < R≤87)的圆形区域.假设节点密度为ρ,网络拓扑如图 1所示.
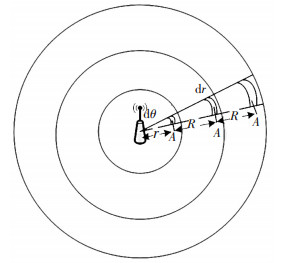
|
图 1 只采用静态sink的网络拓扑图 Figure 1 The network topology with only static sink included |
3) 每个节点以相同的速率产生数据,并且每个节点既能作为数据的源节点又能作为数据的中继节点.
4) sink节点与普通节点相比具有无限数据处理能力、存储容量,以及具有无限制的能量.
5) sink节点的移动速度vM-sink,并且节点数据产生速度μ与发送速度Rt满足一定条件时,sink节点的移动给数据收集带来的影响可以忽略不计.
6) sink节点移动带来的路由重建的能耗忽略不计.
7) 所有传感器节点的结合记为N,对于任意的节点i, j∈N,节点之间的距离记为d(i, j).
2 静态与动态sink相结合的节能策略 2.1 数学模型引理 采用静态与动态sink相结合策略,与只采用静态sink相比,网络生命期将延长至6倍.
证明 先讨论静态sink策略时,sink节点周围的节点的平均能耗.考虑图 2所示的情形,根据1.1节的假设,在以sink为圆心,R为半径的圆内所有节点均可以经过一跳将数据发送至sink.将这些节点的集合记为NSink,NSink={i|d(i, sin k)≤R, i∈N}.任意节点i∈NSink在发送自己产生的数据的同时也将接受并转发来自于外层区域的节点产生的数据.并且由于节点均以R为传输距离,所以只接收距自身距离为R的区域的节点发送的数据.如图 1所示,任选一小区域A1距离sink的距离为r(0 < r < R),且区域A2和A3以及A2到A1的距离均为R.显然A1属于“热点区域”,所以区域A1中的节点记必须转发来自区域A2、A3的数据.由于在静态sink且采用多跳路由的情况下,NSink中的节点承受的能量压力最大,其中的节点能量最先消耗殆尽.为此可以NSink中节点的生命期来表示网络生命期.为了简化处理,假设节点单位时间内的数据为1,并且数据发送能耗为d2,以下分析区域A1中节点的接收以及发送总能耗Er-A1、Et-A1.
| $ {{E}_{r-{{A}_{1}}}}={{E}_{\text{elec}}}\left[\left( r+R \right)\text{d}\theta \text{d}r+\left. \left( r+2R \right)\text{d}\theta \text{d}r \right) \right], $ |
| $ \begin{matrix} {{E}_{t-{{A}_{1}}}}=\left( {{E}_{\text{elec}}}+{{d}^{2}} \right)\left[r\text{d}\theta \text{d}r+\left( r+R \right)\text{d}\theta \text{d}r+ \right. \\ \left. \left. \left( r+2R \right)\text{d}\theta \text{d}r \right) \right]. \\ \end{matrix} $ |
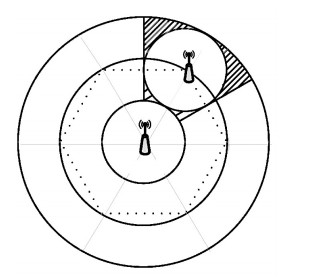
|
图 2 采用动态sink的网络拓扑图 Figure 2 The network topology with mobile sink |
故集合NSink={i|d(i, Sink)≤R, i∈N}的平均能耗E-NSink为
| $ \begin{matrix} {{\overline{E}}_{{{N}_{\text{Sink}}}}}=\frac{\int_{0}^{2\text{ }\!\!\pi\!\!\text{ }}{\int_{0}^{R}{\left( {{E}_{r-{{A}_{1}}}}+{{E}_{t-{{A}_{1}}}} \right)\text{d}\theta \text{d}r}}}{\rho \int{\int{r\text{d}\theta \text{d}r}}}= \\ \frac{\rho \int_{0}^{2\text{ }\!\!\pi\!\!\text{ }}{\int_{0}^{R}{{{E}_{\text{elec}}}\left( 5r+6R \right)\text{d}\theta \text{d}r}+{{r}^{2}}\left( 3r+3R \right)\text{d}\theta \text{d}r}}{\rho \int_{0}^{2\pi }{\int_{0}^{R}{r\text{d}\theta \text{d}r}}}= \\ 17{{E}_{\text{elec}}}+\frac{7}{2}{{R}^{2}}. \\ \end{matrix} $ |
因此,网络生命期为
| $ {{T}_{\text{network}}}=\frac{{{E}_{\text{initial}}}}{{{\overline{E}}_{{{N}_{\text{Sink}}}}}}=\frac{{{E}_{\text{initial}}}}{17{{E}_{\text{elec}}}+\frac{7}{2}{{R}^{2}}}. $ | (1) |
在采用静态sink(S-sink)与动态sink(M-sink)结合的策略ESCMS如图 3所示,S-sink位于网络拓扑的中心处,M-sink位于距离圆心2R处.在第1.1节的假设前提下,由于M-sink节点以一定速度移动并且传感器节点采集数据速率与传输速率满足一定条件时,sink节点移动给数据传输的影响可以忽略,所以每当sink节点到达停靠点时,只有周围的节点向其发送数据.具体来说,图 2中灰色圆代表距离sink节点的距离为R,所以其中的节点可以经过一跳将数据转发至sink,而斜线部分节点的数据则须经过两跳转发.其中灰色密斜线部分的节点将数据发至移动sink,而黑色稀疏斜线部分的感知数据发往静态sink.因斜线区域部分相对来说小得多,所以大部分节点的数据传输都是单跳方式,从而节省了能量.为了方便起见,将灰色密斜线部分的面积记为SM-sink,黑色稀疏斜线部分记为SS-sink.由图 2可知
| $ {{S}_{\text{S}-\text{sink}}}=6\cdot \frac{\sqrt{3}}{4}{{\left( 2R \right)}^{2}}-\text{ }\!\!\pi\!\!\text{ }{{R}^{2}}-6\cdot \frac{1}{3}\text{ }\!\!\pi\!\!\text{ }{{R}^{2}}=0.972{{R}^{2}}, $ |
| $ \begin{matrix} {{S}_{\text{M}-\text{sink}}}=\frac{1}{6}\left[\text{ }\!\!\pi\!\!\text{ }{{\left( 3R \right)}^{2}}-{{R}^{2}} \right]-\text{ }\!\!\pi\!\!\text{ }{{R}^{2}}-\frac{1}{6}{{S}_{\text{S}-\text{sink}}}= \\ 0.885{{R}^{2}}. \\ \end{matrix} $ |
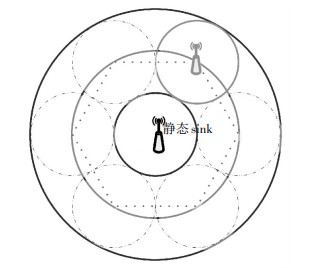
|
图 3 移动与动态sink相结合的节能策略(ESCMS) Figure 3 Energy-saving strategy by combining mobile and static sink scheme |
由于节点均匀分布,静态sink的能耗负载比动态sink高,所以这里用其周围节点生命期来衡量网络生命期.此时静态sink通信半径为R以内的节点集合记为NM-sink,且NM-sink={i|d(i, M-Sink)≤R, i∈N}.所以NM-sink接收能耗Er-M-sink为
| $ \begin{matrix} {{E}_{\text{r-M-sink}}}=\rho {{E}_{\text{elec}}}\left[6\cdot \frac{\sqrt{3}}{4}\left( ^{2}R \right)2-\text{ }\!\!\pi\!\!\text{ }{{R}^{2}}-6\cdot \frac{\text{ }\!\!\pi\!\!\text{ }{{R}^{2}}}{3} \right]= \\ 0.972{{R}^{2}}\rho {{R}^{2}}{{E}_{\text{elec}}}, \\ \end{matrix} $ |
发送能耗Et-M-sink为
| $ \begin{matrix} {{E}_{\text{t-M-sink}}}=\rho \int_{0}^{2\text{ }\!\!\pi\!\!\text{ }}{\int_{0}^{R}{{{r}^{2}}r\text{d}r\text{d}\theta }}+{{\left( \frac{R}{2} \right)}^{2}}\left[6\cdot \frac{\sqrt{3}}{4}{{\left( 2R \right)}^{2}}-\right. \\ \left. 6\cdot \frac{\text{ }\!\!\pi\!\!\text{ }}{3}{{R}^{2}}-\text{ }\!\!\pi\!\!\text{ }{{R}^{2}} \right]\rho . \\ \end{matrix} $ |
集合NM-Sink的平均能耗E-N-M-Sink为
| $ {{\overline{E}}_{\text{N-M-sink}}}=\frac{{{E}_{\text{r-M-sink}}}-{{E}_{\text{t-M-sink}}}}{\rho \int_{0}^{2\pi }{\int_{0}^{R}{r\text{d}r\text{d}\theta }}}=0.077{{E}_{\text{elec}}}+0.58{{R}^{2}}, $ |
此时网络生命期为
| $ {{T}_{\text{M-Network}}}=\frac{{{E}_{\text{initial}}}}{{{\overline{E}}_{\text{N-M-sink}}}}=\frac{{{E}_{\text{initial}}}}{0.077{{E}_{\text{elec}}}+0.58{{R}^{2}}}. $ | (2) |
显然,由式(1)和式(2)可得TM-Network=6.03TNetwork,证毕.
2.2 移动与静态sink相结合的节能策略ESCMS移动与静态sink相结合的策略如下:使用静态sink(记为S-sink)与移动sink(记为M-sink),其中S-sink位于监测区域中心处并且保持静止.距离S-sink节点距离小于R以及处于第二个圆环内到M-sink节点距离小于R将数据发往S-sink.同时M-sink位于距离S-sink节点2R处,如图 3所示.此后,M-sink节点按顺时针方向沿着图 3示的六边形运动,并每次到达一个顶点处则停留一段时间,这段时间内,距离M-sink节点小于R或该距离大于R且处于第三个圆环内的节点均与M-sink进行通信. M-sink的逗留时间确定方法如下:
假设M-sink节点的移动速度为vM-sink,则M-sink节点运动的周期TM-Sink表示为
| $ {{T}_{\text{M}-\text{sink}}}=\frac{6\cdot 2R}{{{v}_{\text{M}-\text{sink}}}}. $ |
假设传感器节点的数据产生数率为μ,则这段时间内传感器节点收集的数据DM-sink为
| $ {{D}_{\text{M}-\text{sink}}}=\frac{\mu \cdot 6\cdot 2R}{{{v}_{\text{M}-\text{sink}}}}. $ |
假设M-sink在每个站点停留的时间为T,并且假设节点用于缓存数据的内存容量为S,则应该满足下列关系:
| $ 6\cdot T\cdot \mu +\frac{\mu \cdot 6\cdot 2R}{{{v}_{\text{M}-\text{sink}}}}\le S. $ | (3) |
另外,假设节点以速率Rt发送数据至M-sink,根据数据量守恒可知
| $ \frac{12\cdot R\cdot \mu }{{{v}_{\text{M}-\text{sink}}}}+6\cdot T\cdot \mu =\frac{T\cdot {{R}_{\text{t}}}}{0.885{{R}^{2}}\rho }, $ |
由此可得
| $ T=\frac{12\cdot R\cdot \mu }{{{v}_{\text{M}-\text{sink}}}\left( \frac{{{R}_{\text{t}}}}{0.885{{R}^{2}}\rho }-6\cdot \mu \right)}. $ | (4) |
由式(3)和式(4)可得
| $ {{v}_{\text{M}-\text{sink}}}\ge \frac{12\cdot \mu \cdot R}{S}+\frac{72\cdot {{\mu }^{2}}\cdot R}{\left( \frac{{{R}_{\text{t}}}}{0.885{{R}^{2}}\rho }-6\cdot \mu \right)\cdot S}. $ | (5) |
由(5)可以获得M-sink的最小移动速度.
若M-sink节点停留时间达到T之后,它将广播一条问询消息,接收到问询消息的节点若有数据尚未发送,则作出答复.否则,简单将问询消息丢弃. M-sink在没收到答复消息时则准备移动到下一站点. 图 3显示M-sink的位置及其通信范围,黑色虚线圆表示M-sink移动过程中的几个不同位置处的通信范围. M-sink的移动轨迹为灰色虚线六边形,并且停靠站点为六边形的顶点.此外,M-sink节点移动过程中不接收数据.
最后,给出M-sink移动时间对网络性能的影响.显然,当满足传感器节点在M-sink节点移动期间采集的数据量远小于逗留期间收集的数据量时,M-sink移动的时间带来的影响可以忽略不计,则
| $ 6T\mu \gg \frac{12\mu R}{{{v}_{\text{M}-\text{sink}}}}. $ | (6) |
根据式(4)和式(6)可得
| $ 12\mu \gg \frac{{{R}_{\text{t}}}}{0.885{{R}^{2}}\rho }. $ | (7) |
同时
| $ {{R}_{\text{t}}}>6\cdot \mu \cdot 0.885{{R}^{2}}\cdot \rho . $ | (8) |
即当节点获取速率和发送速率满足式(7)和式(8)所示条件时,M-sink节点移动带来的影响可以忽略.
3 实验及分析 3.1 性能参数采用NS2进行仿真实验,100个传感器节点独立均匀地分布在为半径l=100 m的区域内.节点的初始能量Einitial为2 J,接收或者发送1 bit数据节点电路所消耗的能量为50 nJ,εamp取值为13 pJ/bit/m2. vM-sink取值为40 m/s,传感器节点的数据采集速率μ以及发送速率Rt取值分别为80和1400 packet/s.
为了评价ESCMS的节能效率,这里定义如下几组性能参数.
网络生命期:传感器网络是以数据为中心的,因此网络生命期对于传感器网络至关重要.对于不同应用场景,网络生命期也不一样.为了使本算法具有普适价值,本文提供如下几个参数作为网络生命期的标准.
首节点能量耗尽时间:表示网络中第一个节点能量耗尽的时间,记为the time when First Node Dies (FND).
半数节点能量耗尽时间:指网络中有一半节点能量耗尽的时间,记为the time when Half of the Nodes Die (HND).
所有节点能量耗尽时间:监测区域中的所有传感器节点能量耗尽的时间,记为the time when the Last Node Dies (LND).显然,当所有节点能量耗尽,WSNs的数据采集功能随之丧失,这必然意味网络生命期的终结.
存活节点数量曲线:WSN中存活节点数量随时间的变化情况,这能直观的反映网络的生命期.比较节点数量曲线可以直观地比较在实验过程中传感器节点的能量消耗情况.
此外,因为WSNs的中心任务就是进行数据采集,定义了如下指标来反映ESCMS的性能.
sink节点吞吐量:sink从监测区域接收的数据量,记为the Throughput of the Sink (TS). WSNs的应用主要建立在sink接收的数据之上,因而比较吞吐量具有实际意义.另外,为了较好地反映能量效率,提出一个相对于能量耗散的吞吐量的概念,即the Throughput of the sink Against Energy consumed(TAE). TAE反映了在相同的能耗下,sink节点获得的数据,显然该指标可以很好地评价能量效率.
最后将仿真结果与静态sink策略(记为S-sink)、移动sink策略进相比较.文献[5]显示该策略可以将网络生命期延长至4倍.所以这里的移动sink策略采用文献[5]中的GMRE策略(记为GMRE).
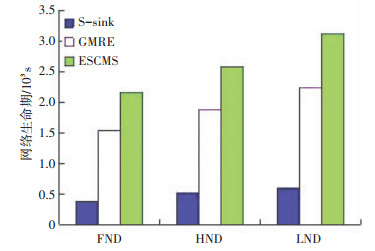
3.2 实验结果分析图 4给出了分别在静态sink、动态sink以及ESCMS策略下的存活节点数量随时间的变化趋势.其中静态采用多跳传输,而移动sink场景采用文献[5]中所采用的GMRE策略.三种策略相应的曲线分别如图 4所示.为了简单起见,三种策略在图中分别记为S-sink、GMRE以及ESCMS.从图 4可以看出,三者的FND分别为385、1530以及2250. ESCMS的FND分别是S-sink的5.84倍,是GMRE的1.47倍. ESCMS的HND是S-sink、GMRE的5.66、2.08倍,LND比关系分别是5.74以及1.39.即使用ESCMS与S-sink相比可将网络生命期延长约6倍,以及比移动sink提升约50%.这与第2节的讨论基本吻合,同时注意到由于移动sink所带来的路由重建开销,而这部分开销理论证明中并未予以考虑,所以实验结果值比理论值偏低. 图 5更为直观地体现了三种策略下,在使用3.1节所定义的生命期定义的对比图.显然,ESCMS的能量效率很显著.
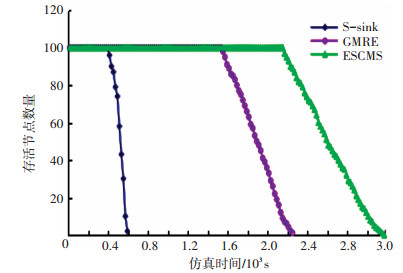
|
图 4 存活节点随时间变化图 Figure 4 The variation of the number of nodes alive with simulation time |
|
图 5 网络生命期对比 Figure 5 The comparison of network lifetime |
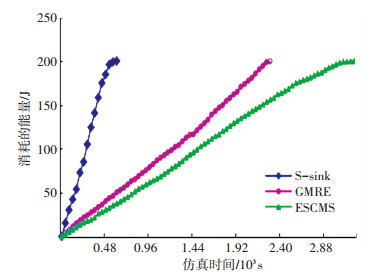
图 6显示了三种情形网络能耗随时间的变化曲线.网络初始总能量为100*2 J,初始状态下,三者的能耗均为0.随着时间推移,S-sink的网络能量耗散速率最快,这从其曲线斜率最大可以看出.同时GMRE居中,而ESCMS最低.这是因为,S-sink策略下“sink邻居问题”无法解决,从而导致能耗最快,同时,GMRE虽然在移动sink的过程中使“sink邻居问题”得以缓解,但因为多跳传输,因而能耗较快.而本文的ESCMS策略采用静态sink与移动sink相结合,有效地缓解了“sink邻居问题”,同时,由于多采用单跳通信,所以其能量消耗速率最低,从而延长了网络生命期.
|
图 6 网络总能耗变化曲线 Figure 6 The energy consumption of the network |
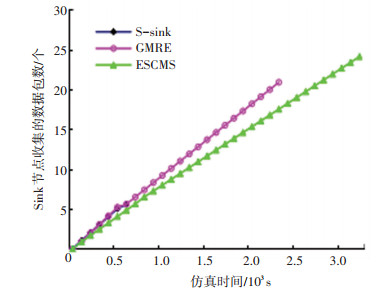
图 7显示三种策略下sink节点接受的数据总量变化曲线.从图 7可以看出:尽管S-sink的曲线较短(由于其网络生命期最短),然而相同时间内其数据量高于GMRE以及ESCMS策略,这是由于后两者移动sink,使得路由重建,同时数据暂缓发送所导致.相对来说,ESCMS所带来的影响最大,因为传感节点均等sink移动到距离在一定区域才将缓存的数据发送.但是,由于其生命期的有效延长,最终所能接受的数据总量是最高的.实验数据显示,ESCMS的数据总量是S-sink的4.63倍,并且是GMRE的1.33倍.即ESCMS相对于前两者可以分别使数据收集量提高363%以及33%. 图 8显示了三者的sink节点相对于能量耗散百分比的吞吐量(TAE).这个指标可以很好地反映出三种策略的能量效能,显然,和另外两者相比,ESCMS在消耗相同能量时,吞吐量远大得多,这说明ESCMS具有较高的能量效率.
|
图 7 sink节点的数据接收量 Figure 7 The amount of data received by the sink |

|
图 8 sink相对能量耗散百分比的吞吐量(TAE) Figure 8 The throughput against the energy of the sink |
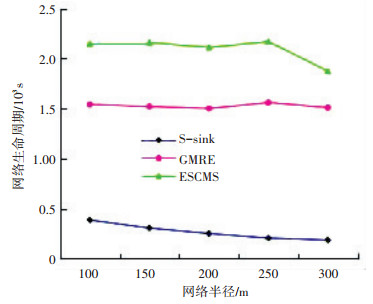
图 9显示了在网络半径时,三者的FND对比图.显然,S-sink的FND值随着网络半径的增大而减小,这是由于随着网络半径增大,跳数增多而加剧了“sink邻居问题”.而GMRE较为稳定,同时ESCMS在半径小于250之前,一直比较稳定,但在250之后FND下降,但一直高于前两者.这是由于随着半径的增大,有些节点必须采用多跳传输,从而能耗较快.这表明:ESCMS适用于半径小于250的网络拓扑,同时整体上,采用ESCMS的能效高于仅仅采用静态sink或动态sink的策略.
|
图 9 网络生命期与网络半径的关系 Figure 9 The relationship between the network lifetime and the network radius |
静态和移动sink相结合的节能策略ESCMS,可以有效节约能量并将WSN的生命期延长至6倍.仿真证实,ESCMS与静态sink相比,可将生命期延长至5.84倍;同时,与移动sink策略GMRE相比,生命期可以提升50%.另外,sink接收的数据总量方面,ESCMS是静态sink的4.63倍以及GMRE的1.33倍.
本文给出的ESCMS策略是在给定网络拓扑下,M-sink节点按照固定的移动路径的一种减少能量消耗不均从而达到延长网络生命期目的的策略.这种方法可以进一步推广到一般拓扑或者更大的检测环境中,只要控制M-sink的移动速率,或者增设M-sink节点个数,同时,使得控制内层和外围M-sink节点的移动速度即可保持本策略的高能效特性.
| [1] | AKYILDIZ I F, SU Weilin, SANKARASUBRAMANIAM Y, et al. A survey on sensor networks[J]. Communications Magazine, IEEE,2002, 40 (8) : 102-114. DOI: 10.1109/mcom.2002.1024422 |
| [2] | RAHEINZALMAN W R, CHANDRAKASAN A, BALAKRISHNAN H. Energy-efficient communication protocol for wireless microsensor networks[C]// Proceedings of the 33rd Hawaii International Conference on System Sciences. Los Alamitos: IEEE Press, 2000: 8020-8030. |
| [3] | BASAGNI S, CAROSI A, MELACHRIOUDIS E, et al. Controlled sink mobility for prolonging wireless sensor networks lifetime[J]. Wireless Networks,2007, 14 (6) : 831-858. DOI: 10.1007/s11276-007-0017-x |
| [4] | ZOLTAN V, ROLLAND V, ATTILA V. Deploying multiple sinks in multi-hop wireless sensor networks[C]// IEEE International Conference on Pervasive Services. Piscataway: IEEE Press, 2007: 55-63. |
| [5] | BASAGNI S, CAROSI S, MELACHRINOUDIS E, et al. A new MILP formulation and distributed protocols for wireless sensor networks lifetime maximization[C]// IEEE International Conference on Communications. Istanbul: IEEE Press, 2006: 3517-3524. |
| [6] | LIANG Weifa, LUO Jun, XU Xu. Prolonging network lifetime via a controlled mobile sink in wireless sensor networks[C]// GLOBECOM-IEEE Global Telecommunications Conference. Miami: IEEE Press, 2010: 1-6. |
| [7] | WANG Wei, VIKRAM S, CHUA K C. Extending the lifetime of wireless sensor networks through mobile relays[J]. IEEE/ACM Transactions on Networking,2008, 16 (5) : 1108-1120. DOI: 10.1109/tnet.2007.906663 |
| [8] | YUN Yongsang, XIA Ye. Maximizing the lifetime of wireless sensor networks with mobile sink in delay-tolerant applications[J]. IEEE Transactions on Mobile Computing,2010, 9 (9) : 1308-1318. DOI: 10.1109/tmc.2010.76 |
| [9] | RAHIM S, RAHIM H, KHAN R D, et al. Circular joint sink mobility scheme for wireless sensor networks[C]// 2015 IEEE 29th International Conference on Advanced Information Networking and Applications Workshops(WAINA). Los Alamitos: IEEE Computer Society, 2015: 311-319. |
| [10] | CHENG Long, CHEN Canfeng, MA Jian. Selection scheme of mobile sinks in wireless sensor networks[J]. Journal on Communications,2008, 29 (11) : 12-18. |
| [11] | SHI Yi, HOU Yongtian. Theoretical results on base station movement problem for sensor network[C]// The IEEE INFOCOM 2008 Proceedings. Piscataway, : IEEE Press, 2008: 376-384. |
| [12] | GANDHAM S R, DAWANDE M, PRAHASH R, et al. Energy efficient schemes for wireless sensor networks with multiple mobile base stations[C]//Global Telecommunications Conferences, 2003. Globecom'03.IEEE. Piscataway: IEEE Computer Society, 2003:377-381. |
| [13] | SHAH R C, ROY S, JAIN S, et al. Data mules: modeling and analysis of a three-tier architecture for sparse sensor networks[C]// Ad Hoc Networks. Holland: Elsevier 2003: 215-233. |
| [14] | MAMALIS B G. Prolonging network lifetime in wireless sensor networks with path-constrained mobile sink[J]. International Journal of Advanced Computer Science & Applications,2014, 5 (10) : 82-91. |
 2016, Vol. 48
2016, Vol. 48


