地震安全性评价是根据建设工程场址周围地震环境调查、地质条件勘测的结果,综合评价和分析计算,最终按照工程类型、性质、重要性,科学合理地给出符合工程抗震设防要求的相应地震动参数.中国相关标准规定对于重大建设工程,必须进行地震安全性评价,并根据该结果指导抗震设防.目前中国地震安全性评价工作一般以基于一致概率谱(UHS)的人造地震动作为基岩面输入,采用一维土层等效线性化方法得到考虑场地反应的地面人造地震动.但人造地震动合成中包络参数的确定和拟合尚没有具体可靠的规定,这种不确定性导致地震安全性评价中给出不合理人造地震动时程的问题时有出现[1].而随着结构动力时程分析的应用日渐广泛,选取天然强震记录的需求变得越来越迫切.虽然现行规范GB 17741-2005《工程场地地震安全性评价》规定:“本地有强震动记录时,宜充分利用其合成适合工程场地的基岩地震动时程”,但由于地震动本身的不可重复性与随机性,在待建工程场地附近很难找到满足设防要求的天然强震记录,目前中国工程场地安全性评价工作中鲜有提供天然强震记录.
随着国内外强震记录不断积累和完善,为研究中国工程场地地震安全性评价中强震记录选取提供了重要的基础数据.现有的天然强震记录选取及修改方法众多,但基本思路一致:首先确定满足设定地震参数的目标谱,进而在强震记录数据库中寻找与目标谱匹配程度满足要求的结果.目标谱是直接决定记录选取结果是否合理的关键因素[2].不少学者已经认识到安全性评价中的一致概率谱是若干设定地震事件综合后得到的包络结果,并无法代表真实的地震动谱形,并不适合指导强震记录选取[3-4].针对上述目标谱存在的问题,2011年Baker[5]同时考虑设定地震信息和地震动固有的离散性,提出了条件均值谱(CMS)概念:从目标结构特性出发将一致概率谱分解为若干条件均值目标谱的组合.条件均值目标谱具有更窄的谱带宽,更明确的物理意义和更合理的形状,近几年在国外得到了广泛实践[6].国内学者也验证了基于条件均值目标谱的选波结果在评估长周期结构响应离散性方面上更加合理[7].
虽然条件均值目标谱得到了不少学者的关注和青睐,但目前中国地震安全性评价工作中并没有将地震动离散性作为单独参数予以考虑,因而该方法一直无法在中国实际应用中推广.为解决上述问题,本文基于中国工程场地地震安全性评价结果给出设定地震信息解耦的思路方法;以某一工程场地作为案例,阐述解耦地震信息,构建条件目标谱和选取强震记录的全过程;对比不同目标谱选波结果差异后,给出适用于中国现行安评工作的天然强震记录选取流程.
1 设定地震解耦设定地震是条件均值目标谱构建以及强震记录选取的基础.中国安全性评价工作给出的设定地震信息仅包含震级和震中距两个参数,主要用于标定人造地震动包络函数.实际观测得到的强震记录表明,即使同一震级,同一震中距下的地震动记录,其反应谱值都可能相差甚巨,这种地震动自身的离散性会直接影响后面强震记录选取和结构响应分析的结果.
McGuire[8]于1995年最先提出了依据概率地震危险性分析(PSHA)结果解耦设定地震的思路,在这一过程中引入了地震动离散性参数.所谓解耦,就是从危险性分析的结果出发,反推出同时满足地震活动性,潜源分布空间相容性的地震参数组合的贡献比例.这种解耦的思路和结果已广泛应用于国外工程实践,是其工程强震记录选取的重要初选依据.美国抗震设计规范(ASCE/SEI-7)[9]中已经明确要求时程分析所选用的地震记录应以该解耦结果得到的最可信地震(MCE)为基础,欧洲抗震规范(Europe-8)[10]、新西兰抗震规范(NZS)[11]等同样规定在强震记录选取时应以该设定地震条件为初步筛选条件.
1.1 标准差系数ε标准差系数ε定义为某设定地震下反应谱目标值与地震动衰减关系均值之间的差值,用标准差的倍数度量,通常用来表征地震动离散性.
| $\ln Sa\left( T \right) = {\mu _{\ln Sa\left( T \right)}}\left( {M, R} \right) + \varepsilon \cdot {\sigma _{\ln Sa\left( T \right)}}.$ | (1) |
式中:(M,R)为设定地震的震级-震中距组合,ln Sa(T)为周期点T处的目标反应谱值,μlnSa(T)和σlnSa(T)为地震动衰减关系在设定地震下的周期点T的均值和标准差.Baker等[12-13]认为,标准差系数ε反映了目标谱值与衰减关系中值在周期点T的差别程度,对地震记录的反应谱形状具有重要影响.若ε为正,表明目标周期处的目标值要大于衰减关系中值,而其他周期点处的反应谱值则要趋近于衰减关系中值,于是在周期点T形成一个“波峰”;反之,对于ε为负的反应谱,会在T处形成“波谷”.
1.2 基于PSHA结果解耦思路依据待建结构特征和危险性分析得到的一致概率谱,确定对应的地震动强度参数(IM, intensity measurement)目标值IMtarget,一般选取目标结构自振周期T1处的一致概率谱值.该目标值的超越概率为
| $\begin{array}{c} P\left( {{\rm{IM}} \ge {\rm{I}}{{\rm{M}}^{{\rm{targer}}}}} \right) = \sum\limits_{i = 1}^n {{v_i}} \iiint {f_M}\left( m \right){f_R}\left( r \right){f_g}\left( \varepsilon \right).\\ P\left( {{\rm{IM}} \ge {\rm{I}}{{\rm{M}}^{{\rm{targer}}}}\left| {m, r, \varepsilon } \right.} \right){\rm{d}}m{\rm{d}}r{\rm{d}}\varepsilon . \end{array}$ | (2) |
式中:n为主要贡献潜源的个数;vi为第i个潜在震源区的地震年平均发生率,取决于该潜源所在的地震带;fM(m)、fR(r)和fε(ε)分别为震级、震中距和标准差系数的概率密度函数.
将式(2)中变量离散化后的概率表达式为
| $\begin{array}{c} P\left( {{\rm{IM}} \ge {\rm{I}}{{\rm{M}}^{{\rm{targer}}}}} \right) = \sum\limits_{i = 1}^n {{v_i}} \sum\limits_{j = 1}^{N1} {\sum\limits_{k = 1}^{N2} {\sum\limits_{h = 1}^{N3} {{P_M}\left( {{m_j}} \right){P_R}\left( {{r_k}} \right)} } } \cdot \\ {P_\varepsilon }\left( {{\varepsilon _h}} \right)P\left( {{\rm{IM}} \ge {\rm{I}}{{\rm{M}}^{{\rm{targer}}}}\left| {{m_j}, {r_k}, {\varepsilon _h}} \right.} \right). \end{array}$ | (3) |
式中:N1、N2、N3分别为震级、震中距和标准差系数的分档数;PM(mj)为某潜源内震级为mj档的概率[14],震级分档时应当符合该潜源的震级上下限约束;将该潜源均匀离散为若干个微元后,各个距离档的微元个数与微元总数之比即为某潜源内震中距为rk档的概率PR(rk);地震动衰减关系的残差可认为服从对数正态分布,标准差系数服从标准正态分布,由正态分布概率密度函数积分即可得到标准差系数在εh档的概率Pε(εh).
P(IM≥IMtarget|mj, rk, εh)计算式为
| $\begin{array}{l} P\left( {{\rm{IM}} \ge {\rm{I}}{{\rm{M}}^{{\rm{targer}}}}\left| {{m_j}, {r_k}, {\varepsilon _h}} \right.} \right) = \\ \;\;\;\;\;\;\;\;\;\;\left\{ \begin{array}{l} 1, \;\;\;\;\;{\rm{IM}}\left( {{m_j}, {r_k}, {\varepsilon _h}} \right) \ge {\rm{I}}{{\rm{M}}^{{\rm{targer}}}};\\ 0, \;\;\;\;其他. \end{array} \right. \end{array}$ | (4) |
根据贝叶斯全概率公式,目标值条件下各个(mj,rk,εh)组合的条件概率P(mj, rk, εh|IM≥IMtarget)如式(5)所示,该条件概率即各设定地震对目标值的贡献比例,是解耦最终得到的结果.
| $\frac{{P\left( {{\rm{IM}} \ge {\rm{I}}{{\rm{M}}^{{\rm{targer}}}}\left| {{m_j}, {r_k}, {\varepsilon _k}} \right.} \right){P_M}\left( {{m_j}} \right){P_R}\left( {{r_k}} \right){P_\varepsilon }\left( {{\varepsilon _h}} \right)}}{{P\left( {{\rm{IM}} \ge {\rm{I}}{{\rm{M}}^{{\rm{targer}}}}} \right)}}.$ | (5) |
上述分析过程表明,解耦所依据的目标值可是任意一个特定周期点的加速度反应谱值,具体的周期点由目标结构决定.
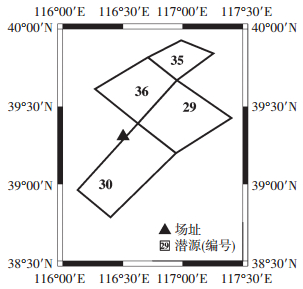
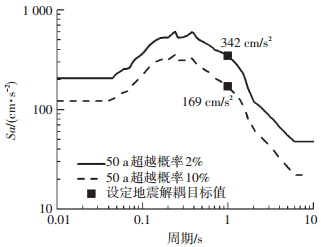
1.3 工程实例分析通过一个工程场地安全性评价实例说明设定地震解耦的过程(数据来源《港清三线输气管道工程地震安全性评价报告》).工程场址和所在区域主要潜源空间位置分布见图 1,涉及的潜源所属地震带均为华北平原地震带,地震活动参数a值为3.79,b值为0.83;地震动衰减关系采用在中国地震安全性评价工程中广泛使用的霍俊荣(1989)衰减关系[15].主要4个潜源对应的震级上限以及空间分布函数列于表 1,工程场址和所在区域主要潜源空间位置分布见图 1,安全性评价中通过概率危险性分析得到的50 a超越概率2%、10%的一致概率谱见图 2.
| 表 1 主要潜源震级上下限以及空间分布函数 Table 1 Magnitude window and distribution function for main earthquake source area |
|
图 1 工程场址及所在区域主要影响潜源划分 Figure 1 Potential source distribution and location of target site |
|
图 2 不同超越概率下的一致概率谱 Figure 2 Uniform spectrum for different exceeding probability |
依据主要潜源的震级上下限和空间范围,确定震级分档范围为[4.5~8],以0.5为分档间隔,每档震级的中值作为该档震级的代表值;震中距r范围为[1~100 km],以5 km作为分档间隔;标准差系数ε区间为[-3~3].假设待建目标结构的自振周期为1.0 s,以加速度谱值Sa(T=1.0 s)为目标值进行设定地震解耦,见图 2.依据式(2)~(5)计算各个潜源下各个可能设定地震事件的贡献比例.
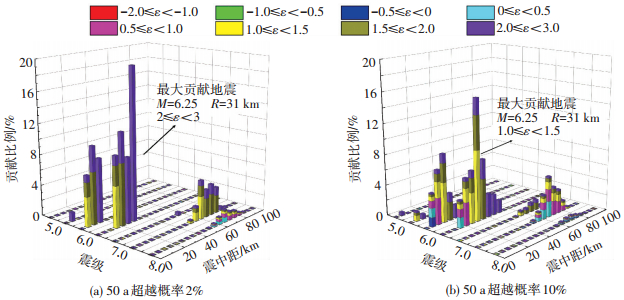
将各个潜源的计算结果进行综合叠加后,得到设定地震事件(M-R-ε)的贡献比例分布见图 3.用不同位置带颜色的三维柱状图表示设定地震组合,x轴代表震级,y轴代表震中距,柱高度代表该事件对目标值的贡献比例,标准差系数用颜色表示,柱高为0表明该事件对目标值没有贡献.各工况下的主要贡献地震集中在M=5.75~6.25,R=15~35 km的区域内,对应的是36号和29号潜源,见图 1;30号潜源虽然距目标场地较近,但由于震级上限仅为6.0,对解耦目标并没有显著贡献,不同解耦目标下的结果差异主要体现在标准差系数上.
|
图 3 50 a不同超越概率下设定地震(M-R-ε)的解耦结果及最大贡献地震 Figure 3 Disaggregation result (M-R-ε) for different exceedance probability and maximum contribution earthquake scenario |
在求解出各可能地震事件的贡献比例后,设定地震的设定思路有两种:最大贡献地震和平均影响地震.最大贡献地震定义为贡献比例最大的(M-R-ε)组合;平均影响地震则是将每个可能的设定地震组合按照贡献比例进行加权平均得到的结果.最大贡献地震和平均影响地震均为危险性分析解耦的重要产出.通常当近、远场同时出现高贡献比例的设定地震组合时,应当给出不同区域对应的最大贡献地震作为设定地震[8].而本文的主要贡献地震事件所在区域相对较为集中,为全面考虑整个潜源区内所有微元对场地的影响特征,宜采用平均影响地震作为设定地震.
不同超越概率的最大贡献地震与平均影响地震结果列于表 2,震级、震中距结果很接近,差异主要集中在标准差系数上,这从另一个角度说明了仅靠震级和震中距并不足以完全描述设定地震,衰减关系离散性对结果的影响不可忽视.正如陶夏新等[16]指出的,PSHA中的目标值已是进行过不确定性校正的结果,如果直接借助衰减关系均值反推设定地震(M, R),得到的结果很容易与地震环境自相矛盾.
| 表 2 最大贡献地震与平均影响地震Sa(T=1.0 s) Table 2 Maximum contribution and median contribution earthquake scenario for Sa (T=1.0 s) |
条件均值谱是以某超越概率下的目标周期反应谱值Sa(T*)为条件,利用地震动衰减关系和相关系数公式计算非目标周期处Ti的反应谱值,从而推导出在整个周期段符合真实谱形规律的反应谱,构造公式为
| $\begin{array}{c} {\mu _{\ln Sa\left( {{T_i}} \right)\left| {\ln Sa\left( {{T^*}} \right)} \right.}} = {\mu _{\ln Sa\left( {{T_i}} \right)}}\left( {{M^*}, {R^*}} \right) + \\ \rho \left( {{T_i}, {T^*}} \right)\sigma \left( {{T_i}} \right)\varepsilon \left( {{T^*}} \right). \end{array}$ | (6) |
式中:(M*-R*-ε(T*))为解耦得到的设定地震;ρ(Ti, T*)为ε(Ti)和ε(T*)的相关系数,采用的是基于NGA-West1数据库拟合得到的经验公式[17],适用范围0.01~10.0 s;μlnSa(Ti)为设定地震(M*, R*)条件下,地震动衰减关系在周期点Ti处的反应谱中值;σ(Ti)为对应的标准差.由式(6)可知,条件均值谱介于一致概率谱和衰减关系均值之间;周期Ti与T*越远,ε(Ti)和ε(T*)的相关性越低,条件反应谱值越接近衰减关系的谱均值,否则条件反应谱值越接近一致概率谱值.
基于前文解耦结果构建的条件均值目标谱见图 4,在目标周期处,条件反应谱均值与目标值一致,随着周期点远离目标周期点,条件均值目标谱逐渐偏离一致概率谱.从整个周期来看,一致概率谱整体偏于保守,这种差异在长周期表现得尤为显著.

|
图 4 一致概率谱,条件均值目标谱与衰减关系均值谱对比 Figure 4 Comparison of uniform spectrum, conditional mean spectrum and mean spectral value of attenuation relationship |
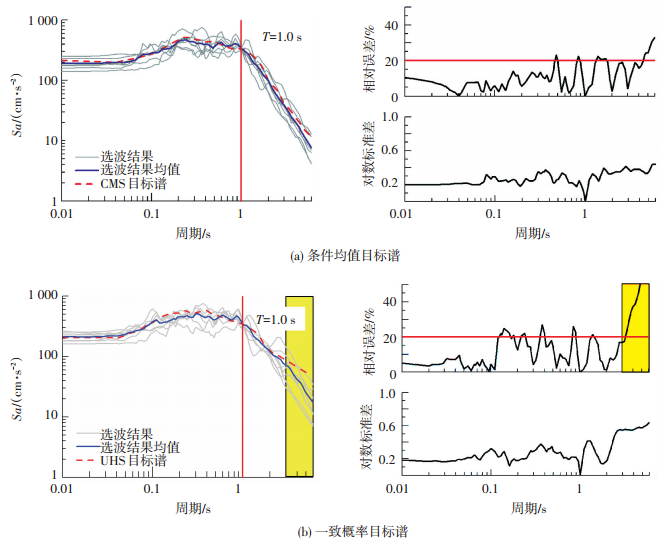
分别选取50 a超越概率2%下Sa(T=1.0 s)的条件均值谱(CMS)、一致概率谱(UHS)作为目标谱进行强震记录选取.强震记录数据库采用的是目前广泛用于工程科研实践且地震信息全面可靠的美国NGA-West1强震记录数据库.首先结合设定地震信息对震级、震中距以及场地条件等重要地震信息参数加以初选.震级范围为设定地震震级±0.5,即M5.7~M6.7;考虑到实际潜源分布和场地的相对位置,以震中距10~100 km为记录筛选范围;由于在PSHA计算过程中包括后面的解耦过程中所用的衰减关系均没有考虑场地的土层放大,只适用于基岩场地,故规定待选记录的台站场地VS30(30 m覆盖土层平均剪切波速)不得低于550 m/s.按上述要求进行震级、震中距、场地条件筛选后,对满足条件的加速度记录以Sa(T=1.0 s)作为目标值进行线性放缩,调幅系数范围为0.5~2.0倍.最后计算所有满足条件记录与目标谱在全周期段的最小均方差,选取全部数据库中均方差值最小的前7条记录作为最终选取结果.这两种不同目标谱下的选波结果见图 5,用选波结果平均反应谱与目标谱的相对误差评价匹配结果在各个周期点的准确性,用选波结果在各个周期点对数值的标准差评价离散性.
|
图 5 不同目标谱下的选波结果 Figure 5 Recordings selection results for different target spectrum |
由图 5可见,基于CMS目标谱的选取结果在绝大多数周期段相对误差保持20%以内,仅在5.0 s之后的相对误差超过了20%,最大相对误差低于30%,对数标准差在0.4以内,均值和离散性的匹配结果均令人满意.而基于UHS目标谱的选取结果,在周期高于3.0 s后选取结果平均反应谱已明显低于目标谱,最大误差达到50%,而且长周期处的对数标准差达到了0.6.从选波结果的地震信息来看,基于UHS目标谱所选记录的震中距整体偏近,7条记录中一半以上的震中距低于15 km,与设定地震信息有明显差距,也不满足实际的潜源分布位置.而基于CMS目标谱的选取结果地震信息整体上与目标值吻合较好,震级与震中距均值与设定地震目标很接近.
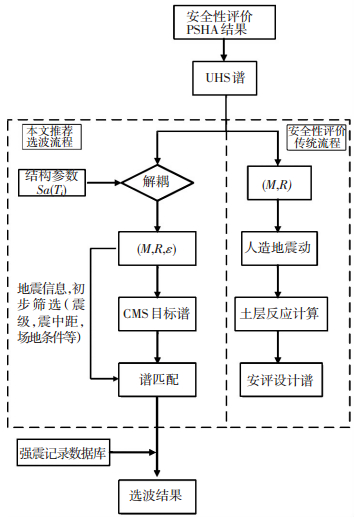
3 地震动选取建议流程将前文基于中国地震安全性评价PSHA分析结果进行强震记录选取的整体流程概括整理为图 6:首先,围绕待建结构的相关参数对PSHA结果进行解耦,整理计算得到对应的设定地震信息(M-R-ε);然后,利用设定地震信息对备选强震记录进行地震动特性方面的筛选后,构建条件均值目标谱进行强震记录匹配.这一选取流程在解耦、筛选记录、目标谱构建的整个过程均兼顾了结构特性和地震动离散性,选取结果作为基岩地震动输入进行土层反应计算后可用于待建结构的时程分析或设计验算中,避免了传统流程中构建规范谱和重复匹配引入的误差.
|
图 6 中国地震安全性评价的天然地震动选取建议流程 Figure 6 Suggested procedure of recordings selection for Chinese seismic safety evaluation work |
1) 基于中国地震安全性评价PSHA的结果实现了同时考虑震级、震中距、标准差系数的地震信息解耦,将各主要潜源离散化得到各个可能的设定地震(M-R-ε)组合对目标值的贡献,得到最大贡献地震和平均影响地震,为构建目标谱和选取强震记录提供考虑结构特性与离散性的设定地震信息.
2) 在中国安全性评价解耦结果的基础上,构建了目前在国外已得到广泛认可和应用的条件均值谱.依据该目标谱选取得到的强震记录结果在地震信息、均值和离散性上均较理想.
3) 在中国地震安全性评价现有工作基础上,作为对人造地震动时程的补充,提出了一套具有操作性的天然强震记录选取流程,可与中国现有安全性评价工作较好衔接.
| [1] |
李小军. 工程场地地震安全性评价工作及相关技术问题[J].
震灾防御技术, 2006, 1 (1) : 15-24.
LI Xiaojun. Evaluation of seismic safety for engineering sites and relevant technical problems[J]. Technology for Earthquake Disaster Prevention, 2006, 1 (1) : 15-24. |
| [2] |
李琳.强震动记录选取中目标谱的研究及应用[D].哈尔滨:中国地震局工程力学研究所, 2015.
LI Ling. Research and application of target spectrum in the selection of strong motion records[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 2015. http://cdmd.cnki.com.cn/Article/CDMD-85406-1015652703.htm |
| [3] | BOMMER J J, SCOTT S G, SARMA S K. Hazard-consistent earthquakescenarios[J]. Soil Dynamics and Earthquake Engineering, 2000, 31 : 611-625. |
| [4] | NAEIM F, LEW M. On the use of design spectrum compatible timehistories[J]. Earthquake Spectra, 1995, 11 (1) : 111-127. DOI: 10.1193/1.1585805 |
| [5] | BAKER J W. Conditional mean spectrum: tool for ground motion selection[J]. Journal of Structural Engineering, 2011, 137 (3) : 322-331. DOI: 10.1061/(ASCE)ST.1943-541X.0000215 |
| [6] | NEHRP (National Earthquake Hazards Reduction Program). Selecting and scaling earthquake ground motions for performing response-history analysis [R]. [S.l.]:National Institute of Standards and Technology, 2011. |
| [7] |
陈波.结构非线性动力分析中地震动记录的选择和调整方法研究[D].北京:中国地震局地球物理研究所, 2013.
CHEN Bo. Ground motion selection and modification methods for performing nonlinear dynamic analysis of buildings[D]. Beijing: Institute of Geophysics, China Earthquake Administration, 2013. http://cdmd.cnki.com.cn/Article/CDMD-85401-1013341977.htm |
| [8] | MCGUIRE R K. Probabilistic seismic hazard analysis and design earthquakes: closing the loop[J]. Bulletin of the Seismological Society ofAmerica, 1995, 85 (5) : 1275-1284. |
| [9] | ASCE/SEI7 05. Minimum design loads for buildings and other structures[S].Reston: American Society of Civil, 2005. |
| [10] | Eurocode 8. European Standard [S]. Brussels: European Committee for Standardization, 2004. |
| [11] | NZS. 1170.5. Structural design actions[S]. Wellington: Standards New Zealand, 2004. |
| [12] | BAKER J W, CORNELL C A. A vector-valued ground motion intensity measure consisting of spectral acceleration and epsilon[J]. Earthquake Engineering and Structural Dynamics, 2005 (34) : 1193-1217. |
| [13] | BAKER J W, CORNELL C A. Spectral shape, epsilon and record selection[J]. Earthquake Engineering and Structural Dynamics, 2006 (35) : 1077-1095. |
| [14] |
高孟潭. 潜在震源区期望震级和期望距离及其计算方法[J].
地震学报, 1994, 16 (3) : 346-351.
GAO Mengtan. Expected magnitude and distance calculation method for potential seismic source region[J]. Earthquake Science, 1994, 16 (3) : 346-351. |
| [15] |
霍俊荣.近场强地面运动衰减规律的研究[D].哈尔滨:中国地震局工程力学研究所, 1989.
HUO Junrong. Study on the near-field strong ground motion attenuation relationship[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 1989. http://d.wanfangdata.com.cn/Thesis_Y129938.aspx |
| [16] |
陶夏新, 陶正如, 师黎静. 设定地震--概率地震危险性评估和确定性危险性评估[J].
地震工程与工程振动, 2014, 34 (4) : 101-109.
TAO Xiaxin, TAO Zhenru, SHI Lijing. Scenario earthquake-link of probabilistic seismic hazard assessment and deterministic seismic hazard assessment[J]. Journal of Earthquake Engineering and Engineering Vibration, 2014, 34 (4) : 101-109. |
| [17] | BAKER J W, JAYARAM N. Correlation of spectral acceleration values from NGA ground motion models[J]. Earthquake Spectra, 2008, 24 (1) : 299-317. DOI: 10.1193/1.2857544 |
 2016, Vol. 48
2016, Vol. 48


