2. 成都市规划设计研究院, 610041 成都
2. Chengdu Institute of Planning and Design, 610041 Chengdu, China
随着社会经济的不断发展,相邻城市之间的联系日益紧密,城际快速路应运而生.城际快速路客运是一种新兴的“公交化”客运发展模式,兼具公路客运和城市公交二者的特点.目前城际快速路客运站点的设置大多凭主观经验,部分站点设置不合理,导致一些沿线居民出行不便,这极大制约了城际快速路客运的发展.目前,对于客运站点设置的研究主要集中在城市公交站点间距[1-3]和选址[4-6]等方面,城际快速路上的站点设置还没有相关研究.为此,借鉴城市公交站点设置的原则和方法,基于集合覆盖原理和灰色聚类理论,提出了城际快速路客运站点的设置方法.
1 城际快速路客运线路分析城际快速路是在城市一体化(或同城化)发展过程中为加强城市之间交通上的便捷联系而修建的,通常道路路段实行半封闭状态,供汽车分向、分车道行驶,道路中央原则上设隔离带,两边不设封闭,设计行车速度可为60、80、100 km/h,机动车道可根据交通需求采用双向10车道、8车道或6车道.通过城际快速路可以建立边缘地区与中心城市互通通道,可以促进城市之间经济的交流,带动城市周边地区经济的发展.
作为一种新的道路形式,城际快速路目前在我国还处在起步阶段,一般修建在城市的外围或相邻城市之间,道路两侧以农田用地为主,建筑用地为辅;沿线不设收费站,在道路等级上一般比高速公路低,部分路段可由高速公路改造而成.我国现已建成的城际快速路有郑州—开封之间的郑开大道、沈阳—抚顺之间的沈抚大道、沈抚二号公路等.城际快速路客运服务于两端城市及沿线居民的公交出行,一般形式为城际公交,如郑开城际公交、沈抚城际公交.城际快速路客运有别于目前的公路客运,借鉴了城市公交的运营模式,具有定线运行、定点停靠、循环发班、票价优惠等特点,更有利于沿线居民出行,如图 1所示.

|
图 1 城际快速路及其客运示意图 |
城际快速路客运线路的起讫点一般为两端城市的重要客运枢纽,按照客运线路途经的区域,可将其分为市区部分和城际快速路部分.在市区部分,线路采用大站运行方式,仅停靠客流密集的站点,站距一般为1~2 km;在城际快速路部分,线路通常根据沿线客流需求大小选择性停靠,站点间距不宜过小,最小站距一般为2 km,同时为提高客运的安全性,站点采用港湾式停靠站.由于两端城市的主要客流集散点已经形成,在市区部分客运站点设置比较明确,可合用部分公交站点.而在城际快速路部分,站点的设置受到沿线居民出行、道路条件以及道路基础服务设施等因素的影响,应满足如下要求:1)站点应设置在靠近居民分布密集,出行率较高的路段,减少沿线居民的出行距离. 2)站点应设置在具有良好线形条件和地形条件的路段,提高客运车辆停靠的安全性. 3)站点应设置在人行横道、地道、天桥等过街设施附近,方便乘客过街.
由于城际快速路两侧大多为农村居民点,传统的城市公交站点选址方法不完全适用.为此,本文针对城际快速路上的客运站点提出了设置方法,该方法以设置最少的站点设施最大化满足沿线居民出行需求为核心目标,同时兼顾了居民出行的方便性和线路运行的高效性.
2 客运站点的设置方法 2.1 居民点集的确定为了避免站点设施的重复建设,在城际快速路两侧的居民点之间寻找可以共用站点的居民点集,并寻找最少数量的居民点集对沿线所有居民点实现全覆盖,具体步骤如下:
1) 城际快速路两侧R(站点服务半径)范围内为城际快速路的影响带状区.
2) 在划定的影响区域内寻找所有可以共用同一个站点的居民点对(集),如图 2所示.对于影响区内分布的任意两个居民点p、q,它们之间的距离为L,根据平面几何原理,如果它们位于城际快速路的同侧,如图 2(a)所示,则这两个居民点共用同一个站点的条件为L2/4+X2≤R2(两居民点连线的中垂线分别与居民点连线、城际快速路相交于两点,X为这两点之间的距离),记为居民点对{p, q};同理,若它们位于城际快速路的异侧,如图 2(b)所示,则这两个居民点共用同一个站点的条件为L≤2R,记为居民点对{p, q}.两居民点位于同侧且连线垂直于城际快速路这种情况是两居民点位于同侧的特殊情况(L≤R).

|
图 2 居民点对(集)构成 |
对于N个居民点(N≥3),如果这N个居民点可以共用同一个站点,则构成一个居民点集.此时,可将居民点对和居民点集统称为广义的居民点集,每个居民点集对应一个客运站点.当N=3时,3个居民点p, q, h构成一个三角形, 如图 2(c)所示,寻找该三角形的外接圆,如果这个外接圆半径小于等于站点服务半径,即R′≤R,则这3个居民点能够共用同一个站点,记作居民点集{p, q, h}.当N>3时,以N=5为例,5个居民点p, q, h, g, k构成一个五边形, 如图 2(d)所示,寻找该五边形的最小外接圆,如果这个最小外接圆半径小于等于站点服务半径,即R′≤R,则这5个居民点能够共用同一个站点,记作居民点集{p, q, h, g, k}.
3) 在所有居民点集的基础上,寻找最少数量的居民点集覆盖所有居民点[7-8].以居民点为行,居民点集为列,建立矩阵A={aij},其中i=1, 2, …, n为居民点编号,j=1, 2, …, m为居民点集编号.若第j个居民点集中包含居民点i,则aij=1,否则aij=0.从矩阵A中选取最少的列组成新的矩阵A1,满足矩阵A1的各行求和均不小于1,此时,所选取的列组成的集合即对应了居民点集的目标集合.
2.2 站点最佳位置选择利用上述方法确定的居民点集与客运站点一一对应,但并未体现站点的具体位置.为了方便居民出行,提高城际快速路客运的吸引力,站点的最佳位置应使得所服务的居民点集内各居民点居民到达该站点的步行总距离最小.假设第j个居民点集内有n个居民点,它们共用站点s,第i个居民点人口总量为Pi,居民出行率为ri,与站点s的步行距离为di,则站点s的服务区域内所有居民点居民到达站点s步行总距离为
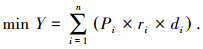
|
(1) |
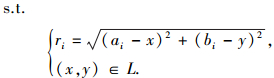
|
以上站点的设置覆盖了沿线所有居民点的居民出行,站点数量一般较多,但出于线路运行的高效性考虑,应选择大站停靠而不宜全部设置.灰色聚类是根据灰色关联矩阵或灰色的白化权函数,将一些观测指标或者观测对象划分为若干个可定义类别的方法[9],是一种综合评价方法,能够自动产生指标权重,减少了评价过程中的主观因素[10].为此,引入灰色聚类方法对这些站点进行重要度评估,按重要程度可将站点分为极端重要、非常重要、重要、一般重要和不重要5类.
设有i(i=1, 2, …, n)个聚类对象;j(j=1, 2, …, m)个聚类指标;k(k=1, 2, …, s)为不同灰类的个数;dij为第i个聚类对象在第j个聚类指标下的样本值,一般通过调查统计得到;fjk为j指标k子类的白化权函数.灰色聚类方法的步骤如下[10]:
1) 指标值和样本值无量纲化处理,构建无量纲化的指标体系和样本白化矩阵D.由于样本值和指标值的量纲不同,数值差异很大,故对数据进行无量纲处理:x′=(x-xmin)/(xmax-xmin).
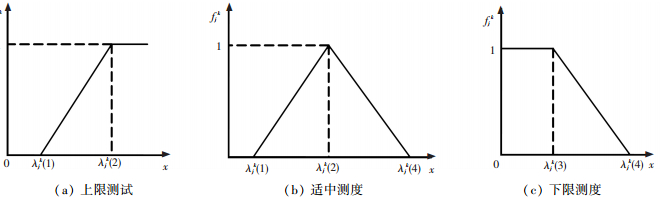
2) 确定灰类白化权函数,即将聚类指标j按照灰类k确定白化函数fjk(dij).一般根据聚类指标和白化数确定上限测度白化权函数、适中测度白化权函数和下限测度白化权函数3类白化权函数(如图 3所示),其函数表达式分别记作fjk[λjk(1), λjk(2), —, —],fjk[λjk(1), λjk(2), —, λjk(4)],fjk[—, —, λjk(3), λjk(4)].
|
图 3 白化权函数 |
3) 计算各指标在各灰类下的权ηjk, 即

|
(2) |
式中ηjk为j指标k子类的权,λjk为j指标k子类的临界值.对于上限测度白化权函数,λjk=λjk(2);对于适中测度白化权函数,λjk=λjk(2);对于下限测度白化权函数,λjk=λjk(3).
4) 计算灰色变权聚类系数σik, 即

|
(3) |
若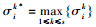
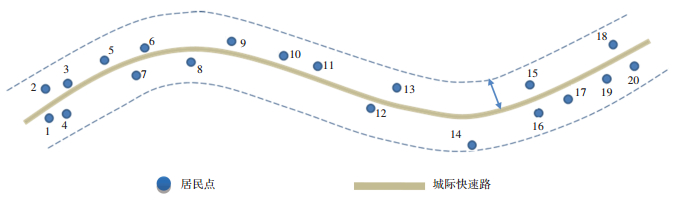
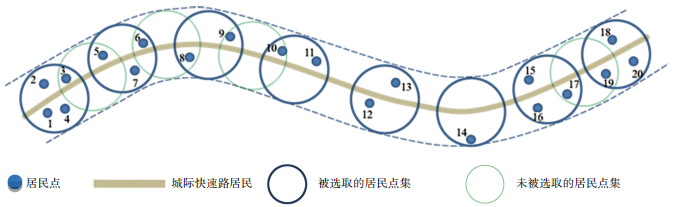
以一条城际快速路为例,在两侧半径为1 km的影响带内分布有20个居民点,居民点编号如图 4所示.选取站点服务半径为1 km,经计算将以上20个居民点划分为12个居民点集,即{1, 2, 3, 4}、{3, 5}、{5, 6, 7}、{6, 8}、{8, 9}、{9, 10}、{10, 11}、{12, 13}、{14}、{15, 16, 17}、{17, 19}、{18, 19, 20},对应的列为j=1, 2, 3, …, 12,因此计算得出矩阵A20×12,如图 5所示.
|
图 4 城际快速路影响带内居民点分布 |
|
图 5 居民点集 |
当从矩阵A中选取第1、3、5、7、8、9、10、12列时,它们所组成的新矩阵A1的各行求和均不小于1,同时8列是所选取的最少列数.因此,该城际快速路设置8个站点将实现对沿线20个居民点的全覆盖,依次编号为s1~s8.根据服务区域内的居民点分布,利用式(1)以居民步行总距离最小为优化目标确定各客运站点的最佳位置,如图 6所示.

|
图 6 城际快速路客运站点的位置 |
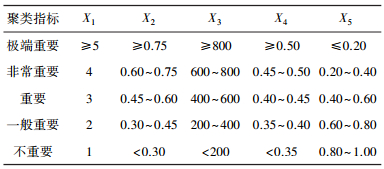
城际快速路客运站点的重要程度与站点所吸引的客流量情况和所处的道路位置等有关.从定量的角度,分别选取站点服务区域内的居民点数量X1(个)、人口数量X2(万人)、地区生产总值X3(百万元/a)、居民出行率X4(次/d)和居民点到站点的平均距离X5(km)作为城际快速路客运站点重要程度的聚类指标.对于各指标的评价阈值,国内外没有相关的标准可参考,因此结合以往的规划经验,建立城际快速路客运站点重要度指标评价体系及标准,如表 1所示.
| 表 1 城际快速路客运站点重要度指标评价体系及标准 |
采用灰色聚类方法对图 6中设置的8个站点进行聚类.聚类对象为站点si,i=1, 2, …, 8;聚类指标为Xj,j=1, 2, …, 5;灰类k=1, 2, 3, 4, 5分别对应极端重要、非常重要、重要、一般重要和不重要.通过调查统计得到每个客运站点服务区内的5类聚类指标值,如表 2所示.
| 表 2 客运站点聚类指标值 |
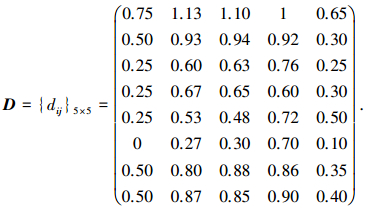
分别对表 1、2中的数据进行无量纲化处理,获取无量纲化的指标值(见表 3)和样本白化矩阵D.考虑到聚类指标X5表示居民点到站点的平均距离越小客运站点重要度越高,因此聚类指标X5无量纲化的指标值与实际值相反.
| 表 3 无量纲化的聚类指标体系 |
|
根据以上指标值和样本值确定j指标k子类的白化权函数分别为

|
由白化权函数可知临界值λjk,利用式(2)计算得权值矩阵H={ηjk}5×5,其中j为行,k为列, 即

|
通过式(3)计算灰色变权聚类系数矩阵Σ={σik}8×5,即

|
对于站点s1,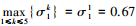
1) 城际快速路是一种新的道路形式,通过分析城际快速路客运线路的运营形式、特点,给出了城际快速路客运站点设置间距、要求的建议.
2) 提出一种寻求最少数量的居民点集对沿线居民点进行全覆盖的算法,有利于实现客运线路的大站停靠;以优化居民点集内居民步行总距离为目标确定站点的最佳位置,极大方便沿线居民的出行;引入灰色聚类法对站点的重要度进行评估,依据每个站点的重要度优化沿线站点的数量,实现快速客运的目的.
3) 案例分析结果表明,该方法实现了城际快速路客运站点位置和数量的优化,满足了沿线居民出行需求和线路快速运行的需要.
| [1] |
WIRASINGHE S C, GHONEIM N S. Spacing of bus-stops for many to many travel demand[J]. Transportation Science, 1981, 15(3): 210-221. DOI:10.1287/trsc.15.3.210 |
| [2] |
SAKA A A. Model for determining optimum bus-stop spacing in urban areas[J]. Journal of Transportation Engineering, 2001, 127(3): 195-199. DOI:10.1061/(ASCE)0733-947X(2001)127:3(195) |
| [3] |
CHIEN S I, QIN Z. Optimization of bus stop locations for improving transit accessibility[J]. Transportation Planning and Technology, 2004, 27(3): 211-227. DOI:10.1080/0308106042000226899 |
| [4] |
谭满春, 徐建闽, 毛宗源. 城市公共汽车停靠点选址模型[J]. 公路交通科技, 1999, 16(2): 59-61. |
| [5] |
王秋平, 丁禹元, 徐乐, 等. 城市公交停靠站选址与平面布置优化[J]. 交通科技与经济, 2011(3): 55-57. |
| [6] |
龚翔, 陈学武, 李娅. 城市快速公交停靠站点在交叉口的选址研究[J]. 土木工程学报, 2011, 44(11): 115-120. |
| [7] |
CEDER A, PRASHKER J N, STERN J I. An algorithm to evaluate public transportation stops for minimizing passenger walking distance[J]. Applied Mathematical Modelling, 1983(7): 19-24. |
| [8] |
CEDER A. Public transit planning and operation:theory, modeling and practice[M]. Amsterdam: Butterworth-Heinemann, 2007.
|
| [9] |
刘思峰, 党耀国, 方志耕, 等. 灰色系统理论及其应用[M]. 北京: 科学出版社, 2010.
|
| [10] |
王媛媛, 陆化普, 秦旭彦. 基于灰色聚类分析的城市交通路网综合评价方法研究[J]. 公路交通科技, 2005, 22(8): 118-121. |
 2016, Vol. 48
2016, Vol. 48