2. 东京大学 生产技术研究所, 153-8505 日本 东京
2. Institute of Industrial Science, University of Tokyo, 153-8505 Tokyo, Japan
汽车排放的颗粒由于粒径小,对人体健康危害极大[1].在地下车库中,由于停车位之间空间狭小,汽车排放颗粒物的扩散在大多数情况下为受限扩散过程.在这种受限扩散条件下,近排气管区域的粒子数浓度和温度很高,在颗粒扩散过程中极易发生凝并.大量的研究结果表明,颗粒凝并作用是产生了较其自身更大颗粒的主要过程之一[2-3];且颗粒凝并对颗粒扩散有重要影响.因此,研究地下车库受限射流下颗粒凝并特性对评估粒子数浓度变化和车库内空气品质具有重要意义.
由于柴油车排放的粒子数浓度要远远高于汽油车,目前国内外对汽车排放颗粒物凝并特性的研究主要集中在柴油车,且为行驶条件下颗粒生成和扩散方面[4-6].大量研究证明,在行驶条件下,由于汽车运动所产生的湍流扰动,颗粒凝并作用并不明显,对颗粒扩散影响很小[7].但地下车库中,汽油车怠速工况下的运行更为普遍.由于汽油车的燃烧效率普遍高于柴油车,汽油车排放颗粒污染物相比于柴油车来说,峰值粒径更小[8-9].对于主要影响颗粒凝并作用的布朗运动而言,颗粒粒径越小,布朗运动越强烈,凝并发生的几率越大.而且,车辆在怠速状态下颗粒排放和扩散相比于运动工况有所不同,由此导致的颗粒凝并发生几率大大高于行驶条件.而现阶段汽油车怠速条件下颗粒受限扩散过程中凝并变化方面的研究还很缺乏,对地下车库这种特殊环境下颗粒凝并和扩散变化规律的认知还很欠缺.
基于以上背景,本文以居民区地下车库中部某停车区域为研究对象,根据颗粒扩散和凝并基本理论,采用数值模拟的方法分析地下车库不同数量车辆怠速运行和受限扩散条件下颗粒半衰时间和粒径变化规律, 为今后更为准确的评估车库内颗粒扩散变化和空气品质提供支撑和依据.
1 数学模型 1.1 湍流模型在封闭的室内环境下,基于雷诺平均Navier-Stokes方程能够精确模拟室内流场和温度场变化[10].本文采用Realizable k-ε 模型来模拟地下车库内流场和温度场的变化.该模型的基本控制方程为
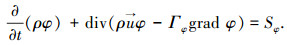
|
(1) |
式中: t为时间; ρ为空气密度; φ代表在x、y和z方向的各参数,包括速度、湍流动能k、湍流耗散率ε和空气焓值h; Γφ为各参数的有效交换系数; Sφ为控制方程源项. 关于Realizable k-ε模型的详细介绍可参阅文献[11].
1.2 颗粒物扩散模型地下车库汽车排出的颗粒物由于粒径小、形状多变,运动和扩散特性十分复杂.为提高数值模拟的计算效率,本文提出如下4点假设并对模型进行简化. 1)颗粒扩散过程中忽略颗粒再悬浮作用. 2)由于颗粒相的体积分数很小,忽略颗粒对流体的作用. 3)颗粒均为球体,且密度不变. 4)在颗粒碰撞过程中,碰撞前后颗粒总质量不变.
本文采用欧拉方法对地下车库颗粒物扩散变化进行数值模拟.欧拉方法是将颗粒相当做充满整个流场空间的连续介质简化方法,认为颗粒相的扩散特性符合被动输运标量特性.但是,由于不同粒径颗粒的运动规律有所差别,模拟过程中应考虑颗粒相的受力对其扩散的影响.对于颗粒而言,其所受到的流体拽力和重力最为重要.因此,本文在颗粒扩散过程中,考虑流体拽力和颗粒重力对颗粒物扩散特性的影响,给出各离散段颗粒相运动扩散的控制方程为
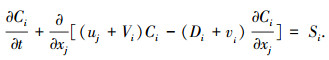
|
(2) |
式中: Ci为各离散段粒子数浓度(i=1, 2, …, 9);xj(j=1, 2, 3)为x、y和z方向的坐标; uj代表x、y和z方向上的速度分量; Vi为重力作用下颗粒沉降速度; Di为各离散段颗粒分子扩散系数; vi为各离散段颗粒湍流扩散系数; Si为各离散段颗粒变化源相.其中重力作用下颗粒沉降速度Vi、颗粒分子扩散系数Di和湍流扩散系数vi可按文献[12-13]给出的方法进行计算.
1.3 颗粒物凝并模型本文采用由于颗粒分子扩散引起的布朗凝并理论计算地下车库颗粒凝并变化.布朗凝并作用下各离散段粒子数浓度变化 Si 的计算式为
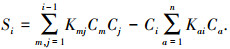
|
(3) |
式中: Kmj、Kai均为不同离散段的颗粒凝并系数; Cm、Cj、Ca 和Ci均为不同离散段粒子数浓度.
颗粒凝并系数Kij 的计算式为[16]
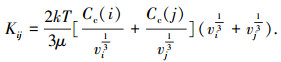
|
(4) |
式中: k为玻尔兹曼常数,k= 1.380 7×10-23 J/K; T为空气温度; μ为空气动力粘度; vi、vj分别代表离散段i和离散段j颗粒体积; Cc(i)、Cc(j)分别为离散段i和离散段j库宁汉修正系数.
根据假设(4),颗粒碰撞凝并过程中质量守恒.则各离散段颗粒经过凝并后,生成新颗粒的粒径dk的计算式为
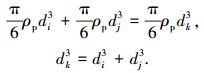
|
(5) |
式中:ρp为颗粒密度;di、dj均为离散段颗粒直径.
2 物理模型本文的计算对象为某居民区地下车库中部区域.模型长宽高分别为17.5、9.8、4.2 m. 6台相同尺寸的汽油车停放在模型中部.汽车的长宽高分别为4.5、1.8、1.5 m.排气管的直径为0.05 m,离地高度为0.3 m.本文的物理模型详见图 1.本文通过对居民区地下车库长达1 a的环境测试发现,出于经济因素等考虑,居民区地下车库全年几乎不运行机械通风系统,车库内为自然通风条件.因而图 1的计算模型中并未开启通风系统.
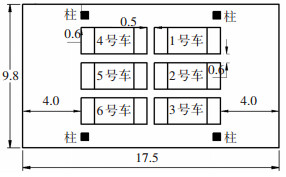
|
图 1 模型的几何尺寸(m) |
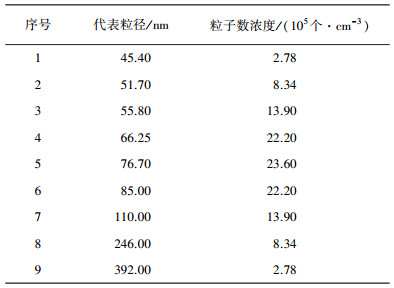
本文采用Realizable k-ε 模型和带有场函数的被动输运标量模型模拟稳态情况下空气流场、温度场和颗粒浓度场的变化.其中顶棚、地面和汽车表面为无滑移墙边界.垂直方向包围模型的4个表面均为流量分配出口边界.本文根据怠速启动车辆数建立4个算例.其中算例1为1号车启动,算例2为1号车和4号车启动,算例3为1号车、2号车、4号车和5号车启动,算例4为1~6号车全部启动.在各算例中,启动车辆的排气管设定为速度入口边界,不启动车辆的排气管设定为墙边界.各边界值和计算初始值详见表 1.汽车排气口排放颗粒粒径分布如表 1所示[14].
| 表 1 各离散段代表粒径和粒子数浓度 |
模拟过程中,汽车排气管排气速度、出口温度分别为1.56 m/s和303.15 K,汽车排气前背景环境中各离散段粒子数浓度和温度分别为2.72×103个/cm3和281.56 K,背景环境中 x 方向速度为0.07 m/s,其他方向均为0 m/s.本文采用商业流体模拟软件STAR CCM+ 8.02进行数值模拟计算.
本文对所建模型进行六面体网格划分,将模型中汽车排气管附近区域进行网格加密处理.同时在不同网格数条件下,通过对算例1的模拟来进行无关性检验.网格无关性检验的结果见图 2. 图 2表明,150万网格数条件下,模型中颗粒平均计数浓度和沿排气管中心线0.3 m处的计数浓度与200万和250万网格数条件下基本相同. 150万网格数对于本文的研究已经足够精确.因而,数值模拟所需的网格数确定为150万左右.
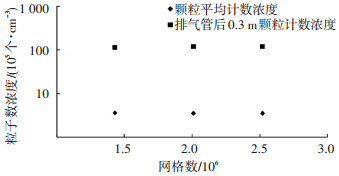
|
图 2 网格无关性检验 |
本文同时通过与Ning等[15]在怠速状态下测得的沿排气管中心的粒子数浓度分布特性对比,对所建模型进行验证.由于Ning等的测试中缺失排气口位置的颗粒粒径分布,多分散颗粒凝并理论不再适用.本文假设排气口排出颗粒为单分散的,粒径均为60 nm,并在模型验证中运用单分散颗粒凝并理论计算颗粒凝并变化.在单分散颗粒凝并条件下,粒子数浓度的变化 S 可按下式计算.
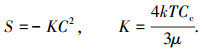
|
(6) |
式中:K为颗粒凝并系数;C为粒子数浓度;Cc为颗粒的库宁汉修正系数.
图 3给出了数值模拟结果与实验值的比较.从图 3可以看出,本文建立的模型可以很好地模拟颗粒沿排气管中心线的变化趋势,但在大部分测点中,模拟值要略大于实验值.这是由于单分散凝并理论分析得到的粒子数浓度减少量低于真实情况所致[16-17]. 图 3的结果表明,本文所建立的模型能很好模拟粒子数浓度的变化规律.
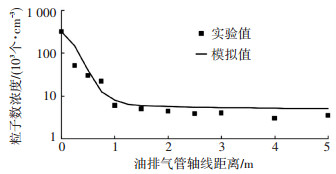
|
图 3 数值模拟结果与实验值比较 |
本节根据数值模拟结果,分别对算例1~4条件下颗粒半衰时间变化和由凝并导致的颗粒粒径分布变化进行详细分析.
3.1 颗粒半衰时间变化颗粒半衰时间是指粒子数浓度变化达到稳定时停止车辆启动,由凝并作用导致的原各离散段粒子数浓度之和降低到一半时所需的时间,是评价颗粒凝并变化的重要指标.颗粒半衰时间越短,则凝并作用越强.
图 4为不同启动车辆条件下1号车排气管纵截面中心的颗粒半衰时间分布. 图 4的结果表明,不同启动车辆条件下,在靠近1号车排气管的区域内颗粒半衰时间最短,均为175 s.这说明由于排气管附近的颗粒温度高、计数浓度大,凝并作用在1号车排气管附近最强.在不同启动车辆数的算例中,由于1号车排放的颗粒参数保持不变,启动车辆数增加对排气管附近凝并作用没有影响.在垂直方向上,除排气管附近区域外,随高度增加,颗粒半衰时间逐渐减少.这说明由于排气颗粒和周围环境的温差产生的热浮力促使颗粒向上扩散,车库顶部的粒子数浓度高,凝并作用明显.启动车辆数越多,同一高度下颗粒的半衰时间越短.这说明随着模型中颗粒源不断增多,粒子数浓度增加,凝并作用加强.
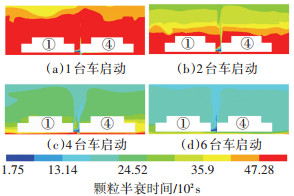
|
图 4 1号车排气管纵截面中心的颗粒半衰时间 |
图 5为不同启动车辆条件下停车位中间区域排气管横截面中心的颗粒半衰时间分布.与图 4所示的纵截面颗粒半衰时间分布类似,在各启动车辆排气管附近的区域,颗粒半衰时间最短,为175 s. 图 5(a)、5(b)的结果表明,当启动车辆小于2台时,颗粒凝并作用明显的区域局限于启动车辆的周围. 图 5(b)的结果还表明,在两台位置相对的启动车辆中间区域,颗粒半衰时间沿车辆中心线近似对称分布. 图 5(c)的结果表明,当模型中启动车辆为4台时,颗粒凝并明显的区域已扩散到未启动5号和6号的车中间区域.上述结果说明,随着模型中启动车辆增多,颗粒源和流场中热源增加,颗粒扩散作用增强,在未启动车辆的中间区域,颗粒扩散导致计数浓度升高,凝并作用增强. 图 5中的结果还表明,随着启动车辆数的增加,横截面相同位置的颗粒半衰时间逐渐缩短.这同样证明了随着颗粒源和流场中热源的不断增加,凝并作用增强.
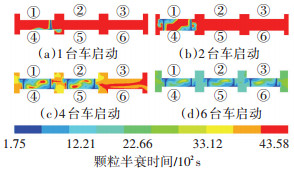
|
图 5 排气管横截面中心颗粒半衰时间 |
在地下车库中,沿高度方向2 m以下的区域是人活动的主要区域,该区域内颗粒半衰时间的分布特性对粒子数浓度分析和空气环境评价具有重要意义. 图 6为沿高度方向2 m以下区域内,不同启动车辆条件下各高度的颗粒平均半衰时间分布.在不同启动车辆条件下,随着高度的增加,颗粒半衰时间均逐渐减小.其中1台车或2台车启动时,颗粒半衰时间随高度近似线性下降. 4台车或6台车启动时,颗粒半衰时间在高度方向变化率略有差别,可近似看成对数变化.当高度小于0.5 m时,颗粒半衰时间下降很快;当高度大于0.5 m时,颗粒半衰时间变化很小.这是由于车库顶棚会限制颗粒沿高度方向的扩散,导致颗粒自上而下的产生堆积.随着启动车辆的增加,颗粒源和流场中热源增多,由热浮力导致的颗粒向上扩散增强,导致颗粒自上到下的堆积作用加强,在沿高度方向0.5~2 m范围内,粒子数浓度更为均匀,半衰时间变化不大.启动车辆数越多,颗粒半衰时间沿高度方向下降越明显.当启动车辆数从1台变化为6台时,2 m高度位置的颗粒半衰时间分别为地面附近半衰时间的59.9%、52.6%、49.4%和48.3%.这表明,随着启动车辆数增加,2 m高度粒子数浓度升高,凝并作用增强.
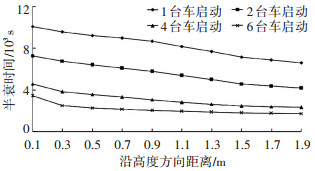
|
图 6 2 m以下区域颗粒平均半衰时间沿高度分布 |
随着颗粒凝并的进行,颗粒粒径分布会发生明显的变化.在本文的模型中,排气口排放的颗粒是唯一的颗粒发生源,且表 1中的排气口各离散段粒子数浓度之和要比表 2中的模型各离散段颗粒初始浓度之和高1个数量级,若不考虑凝并作用,模型在稳态条件下的颗粒粒径分布应与排气口处的颗粒粒径分布相同. 图 7为不同启动车辆条件下排气口和模型各离散段颗粒体积平均计数浓度与谷值段1之间的比值. 图 7中离散段1~3的比值与排气口处大体相同,而离散段4~9的比值为10~20,远远高于排气口处数值(1~10).这说明随着凝并作用的进行,中间段和大粒径段粒子数浓度的变化与小粒径段相比更明显.不同启动车辆数在稳态条件下颗粒平均计数浓度峰值所在的粒径段均由段5变化为段7,增加1.43倍,颗粒粒径分布呈现出由小变大的趋势.
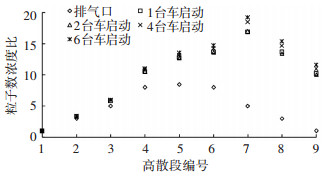
|
图 7 各离散段与段1的粒子数浓度比 |
图 7中的数据还表明,各离散段比值随启动车辆的增加而增加,这是由于随着启动车辆的增加,颗粒凝并作用增强,各离散段由凝并导致的粒子数浓度变化更明显,与谷值段1之间的比值更大.当启动车辆数由1台增加到6台时,峰值段7的比值变化最为明显,由16.9升高到19.2,增加1.14倍. 图 7的模拟结果说明,在稳态条件下,凝并作用导致的中间段和大粒径段粒子数浓度的增加更为明显.启动车辆越多,由凝并导致的各离散段粒子数浓度与谷值之间的比值越大.
4 结论1) 在排气管附近,颗粒半衰时间最短,凝并作用最强.在垂直方向上,除排气管附近区域外,随高度增加,颗粒半衰时间逐渐减少.在位置相对停放的启动车辆中间,颗粒半衰时间沿车辆中心线近似对称分布.启动车辆数越多,相同位置的颗粒半衰时间越短,凝并作用越强.
2) 在沿高度方向2 m以下的区域内,当启动车辆数不大于2台时,颗粒半衰时间随高度近似线性下降;当启动车辆数为4台以上时,颗粒半衰时间随高度近似对数下降.当地下车库中1台车启动、2台车启动、4台车启动、6台车启动时,2 m高度位置的颗粒半衰时间分别降低为地面附近半衰时间的59.9%、52.6%、49.4%和48.3%.
3) 在稳态条件下,凝并作用导致的中间段和大粒径段粒子数浓度的变化与小粒径段相比更明显.不同启动车辆条件下,颗粒平均计数浓度峰值所在的粒径段由段5变化为段7,增长1.43倍,颗粒粒径分布呈现出由小变大的趋势.各离散段与谷值段1计数浓度的比值随启动车辆的增加而增加,其中峰值段7的比值增加最为明显.当1台车启动增加到6台启动时,段7与段1的比值由16.9升高到19.2,增加1.14倍.
| [1] |
PETERS A, VON K S, HEIER M, et al. Exposure to traffic and the onset of myocardial infarction[J]. The New England Journal of Medicine, 2004, 351(17): 1721-1730. DOI:10.1056/NEJMoa040203 |
| [2] |
KITTELSON D B. Engines and nanoparticles:a review[J]. Journal of Aerosol Science, 1998, 29(5/6): 575-588. |
| [3] |
RISTOVSKI Z D, MORAWSKA L, HITCHINS J, et al. Particle emissions from compressed natural gas engines[J]. Journal of Aerosol Science, 2000, 31(4): 403-413. DOI:10.1016/S0021-8502(99)00530-3 |
| [4] |
KIM D, GAUTAM M, GERA D. Parametric studies on the formation of diesel particulate matter via nucleation and coagulation modes[J]. Journal of Aerosol Science, 2002, 33(12): 1609-1621. DOI:10.1016/S0021-8502(02)00119-2 |
| [5] |
李新令. 发动机超细颗粒排放特性及其在排气稀释过程中的变化研究[D]. 上海: 上海交通大学, 2007.
|
| [6] |
KIM D, GAUTAM M, GERA D. Modeling nucleation and coagulation modes in the formation of particulate matter inside a turbulent exhaust plume of a diesel engine[J]. Journal of Colloid and Interface Science, 2002, 249(1): 96-103. DOI:10.1006/jcis.2002.8264 |
| [7] |
UHRNER U, LÖWIS S V, VEHKAMÄKI H, et al. Dilution and aerosol dynamics within a diesel car exhaust plume:CFD simulations of on-road measurement conditions[J]. Atmospheric Environment, 2007, 41(35): 7440-7461. DOI:10.1016/j.atmosenv.2007.05.057 |
| [8] |
WEHNER B, UHRNER U, LÖWIS S V, et al. Aerosol number size distributions within the exhaust plume of a diesel and a gasoline passenger car under on-road conditions and determination of emission factors[J]. Atmospheric Environment, 2009, 43(6): 1235-1245. DOI:10.1016/j.atmosenv.2008.11.023 |
| [9] |
潘锁柱, 裴毅强, 宋崇林, 等. 汽油机颗粒物数量排放及粒径的分布特性[J]. 燃烧科学与技术, 2012, 18(2): 181-185. |
| [10] |
ZHANG Z, CHEN Q. Comparison of the eulerian and lagrangian methods for predicting particle transport in enclosed spaces[J]. Atmospheric Environment, 2007, 41(25): 5236-5248. DOI:10.1016/j.atmosenv.2006.05.086 |
| [11] |
王福军. 计算流体动力学分析-CFD软件原理与应用[M]. 北京: 清华大学出版社, 2006.
|
| [12] |
WILLIAM C H. Aerosol technology[M]. New York: John Wiley and Sons, 1982: 260-277.
|
| [13] |
FAN Long, XU Nong, KE Xiyong, et al. Numerical simulation of secondary sedimentation tank for urban wastewater[J]. Journal of the Chinese Institute of Chemical Engineers, 2007, 38(5/6): 425-433. |
| [14] |
高继东, 宋崇林, 张铁臣, 等. 汽油车排气中颗粒物粒径的分布特性[J]. 燃烧科学与技术, 2007, 13(3): 248-252. |
| [15] |
NING Z, CHEUNG C S, LU Y, et al. Experimental and numerical study of the dispersion of motor vehicle pollutants under idle condition[J]. Atmospheric Environment, 2005, 39(40): 7880-7893. DOI:10.1016/j.atmosenv.2005.09.020 |
| [16] |
MILLER S E, GARRICK S C. Nanoparticle coagulation in a planar jet[J]. Aerosol Science and Technology, 2004, 38(1): 79-89. DOI:10.1080/02786820490247669 |
| [17] |
LEE K W, CHEN H. Coagulation rate of polydisperse particles[J]. Aerosol Science and Technology, 1984, 3: 327-334. DOI:10.1080/02786828408959020 |
 2016, Vol. 48
2016, Vol. 48