3D物体的骨架类似于二维情形下的中轴线, 可以形象地表述物体的拓扑特征, 被广泛应用于计算机动画、机械设计、医学图像、虚拟导航和虚拟内窥镜等技术领域[1].目前, 骨架提取的方法可以根据输入数据类型的不同来划分.文献[2]针对计算机动画中的三角网格面数据计算出数据的voronoi图, 应用平均曲率对其进行边缘划分, 进而得到离散的骨架点; 文献[3]针对三维激光扫描技术获得的点云数据利用马尔可夫随机场模型的3D非刚性匹配技术追踪点云数据, 得到的轨迹即为物体骨架; 此外, 还有CT、MRI等序列扫描图像合成的体数据, 由于体数据可以完整保留物体的内部信息, 在医学图像可视化和生物信息等方面都具有重要意义.
针对于体数据的骨架提取方法主要包括:拓扑细化法, 如文献[4]中反复剥离物体的最外层体素, 直至单连通即为骨架; 距离场方法, 如文献[5]对数据进行距离变换, 抽取出局部距离极大点作为骨架点.但文献[6]表示以上两种方法所提取出的骨架易受噪声干扰.因此, Cornea ND等人提出了势能场方法[7], 综合考虑到所有表面点的影响, 而不像距离场只考虑距离最近的单个表面点, 因此该方法具备更好的鲁棒性.但实验表明, 运用该方法作用于256×256×487的虚拟人体数据时, 需要耗费5 h, 这在临床应用中是无法忍受的.因此, 本文提出基于图形处理器(GPU)的势能场骨架提取并行算法, 并加入CUDA架构特有的存储器结构来优化算法, 讨论了如何根据显卡设备和程序的固有属性来分配线程以达到最高的GPU占用率, 从而得到更优的加速效果.
1 势能场骨架提取方法物体的骨架需要具备以下特性:1)纤细性, 凝练出物体的基本结构; 2)连通性, 若物体本身是连通的, 则骨架也同样是连通的; 3)中心性, 骨架应处于物体的核心位置上.针对体数据而言, 骨架指的是由单体素组成的、连通的、位于物体中心的一序列体素[8].
Cornea ND提出的势能场方法假设物体表面遍布同种点电荷, 作用于物体内部, 从而形成静电斥力场.通过计算各点在势能场中的受力情况, 选取特殊的点作为种子点, 连接这些点形成3D物体的核心骨架.具体步骤如下:
1) 将体数据中的各个离散体素点分类为外部点、表面点、边界点和内部点.外部点是体素值为0的点; 表面点是指其26邻域中至少存在一个外部点; 边界点是指其26邻域中至少存在一个表面点; 其余的均为内部点.
2) 势能场的计算.内部点或边界点P会受到周围的表面点C所带来的斥力, 该斥力与距离成反比, 计算公式为
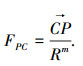
|
式中: 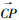
3) 选取场值为0且场方向发生改变的点为关键点.首先检测一个立方体区域内的8个顶点, 若场值在X, Y, Z方向上均发生改变, 则该区域中可能存在关键点, 迭代划分立方体, 直至得到一个不可分的体素点为止.接着计算该点势场力的雅克比矩阵, 根据以下定义将关键点分类:
定义1 雅克比矩阵特征值的实部和虚部均为负时, 该点称为吸引点, 其周围所有向量都指向该点.
定义2 雅克比矩阵特征值的实部和虚部均为正时, 该点称为排斥点, 其周围所有向量都背离该点.
定义3 雅克比矩阵特征值的实部和虚部有正有负时, 该点称为鞍点, 其周围向量有的指向该点, 有的背离该点.
4) 骨架生长和骨架连接.遍历所有鞍点, 每个鞍点均生成一个骨架段.从鞍点出发, 以正特征值对应的特征向量为方向, 使用力跟随法按照一定的步长前进.连接所有鞍点形成骨架.
2 基于GPU的势能场骨架提取并行算法通过实际运行发现, 势能场的计算占据了整个提取过程98%的时间, 因此, 减少骨架提取时间的核心思想就是加快势能场的计算.
2.1 并行性分析计算势能场时, 需要针对每一个内部点或边界点, 扫描所有表面点.因此, 势能场的求解过程中存在两层循环:外层循环是遍历所有内部点或边界点, 求得各个点的势场力; 内层循环是遍历每个表面点, 计算每个表面点对该内部点或边界点的影响.计算公式如下:
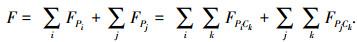
|
(1) |
其中, i为内部点, j为边界点, k为表面点, 势能场计算的时间复杂度是Ο((i+j)×k).由式(1)可知, 势场力的计算具备独立性, 点与点之间不互相影响, 因此可以将原本的串行计算并行化.通常情况下, 内部点和边界点的个数大于表面点的个数, 外层循环的计算量更大, 于是本算法将外层循环放至GPU中, 为每一个内部点和边界点分配一个线程, 将时间复杂度降至Ο(k), 且k远小于(i+j).另外, 根据定义可知边界点处于表面点和内部点之间, 而计算平均值要比计算距离简单很多, 于是本算法将边界点26邻域点的平均势场力作为该点的势场力, 此过程同样放至GPU中.
2.2 算法流程在基于GPU的并行系统中, CPU和GPU各司其职, CPU负责复杂的流控制等需要串行处理的部分, 而密集型数据的并行计算部分则交由GPU完成[9].有别于原始的串行算法, 本文中CPU只负责简单的体素点划分, 而复杂的势场力计算则交由GPU完成.计算时将各个内部点和边界点平均分配给每个线程, 多线程并行执行.具体的程序流程见图 1.

|
图 1 GPU并行的势能场骨架提取流程图 |
在CUDA架构中存在多种存储结构, 按照存取速度由快到慢排列依次是:寄存器(Register)、常量存储器(Constant Memory)、共享存储器(Shared Memory)、纹理存储器(Texture Memory)、局部存储器(Local Memory)和全局存储器(Global Memory).
在普通的并行算法中, 仅仅使用了寄存器和全局存储器, 为了进一步加快程序的运行速度, 提出了改进的并行算法.结合算法本身的特点, 使用了访问速度可以与寄存器媲美的常量存储器和共享存储器.
首先, 对于每个内部点而言, 周围的表面点个数有限, 数据量小于常量存储器的容量64 kB, 并且表面点仅用于读取, 并不对其改写, 因此可以将表面点的信息存储在常量存储器中以加快内部点的势场力计算.另外, 在程序执行过程中, 需要频繁地访问全局存储器来修改势场力数组的值, 这无疑会带来较大的延迟, 因此在改进算法中将势场力数组移入到共享存储器中.
2.4 线程分配对于串行程序而言, 程序的执行时间可以表达为关于问题规模(即输入数据规模)的函数, 而对于并行程序而言, 执行时间不仅与问题规模相关, 还与并行体系结构相关, 而GPU的占用率(occupancy)就是其中一个重要的考虑参数[10], 计算公式如下MP(Multiprocessor):

|
(2) |
其中, Warps per Block=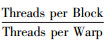
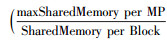
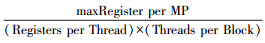
maxRegister per MP, maxSharedMemory per MP和maxThreadBlocks per MP分别表示最大寄存器数量、最大共享存储器容量以及最大线程块数目, 其值均取决于显卡的规格参数; 而Registers per Thread和SharedMemory per Block则表示程序运行中实际用到的寄存器数量和共享存储器的容量, 其值均由CUDA在启动线程时自动分配.
由此可知, 对于不同的显卡设备, 可先将显卡和程序本身的固有属性参数代入式(2), 计算出合适的Threads per Block值即每块线程数, 以达到最优的GPU占用率, 从而得到更好的加速效果.
3 实验结果与性能分析 3.1 实验环境开发平台为3.33 GHz Intel(R) Xeon(R) X5680双核CPU, 24G内存, 显卡分别为NVIDIA Quadro FX 5800和NVIDIA GeForce GTX 580, 显卡的各项参数如表 1所示.开发工具为Microsoft Visual Studio 2010和CUDA4.0.
| 表 1 显卡的规格参数(MP: Multiprocessor) |
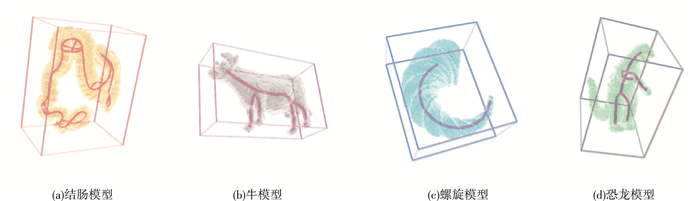
图 2显示了本程序的骨架提取结果, 采用的体数据来自于文献[6], 分别是含有91 329个边界点, 大小为204×132×260的结肠模型; 含有6 555个边界点, 大小为85×31×54的牛模型; 含有9311个边界点, 大小为87×74×45的螺旋模型; 含有6 986个边界点, 大小为54×87×75的恐龙模型.
|
图 2 GPU并行的势能场骨架提取结果 |
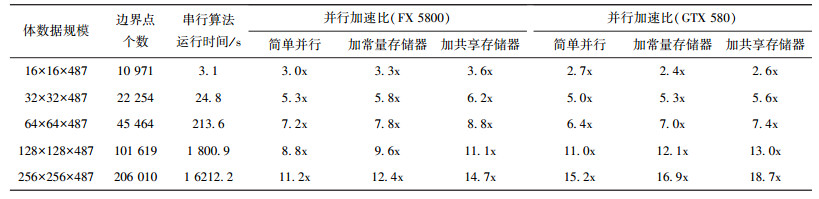
在不同的输入数据规模下, 普通并行算法和改进并行算法的加速比结果如表 2所示.将Threads per Block和Blocks per Grid均设定为128, 分别在显卡FX5800和GTX580上进行测试, 均得到了较好的加速效果, 说明本算法不受显卡设备的制约.算法的加速比随着数据规模的增大而逐渐提升, 当数据规模达到256×256×487时, 普通并行算法在两种显卡上分别可以达到11倍和15倍的加速比, 而加入了常量存储器和共享存储器的改进算法又进一步将加速比提升了20%左右, 分别达到了15倍和18倍.
| 表 2 普通并行算法与改进并行算法的加速比 |
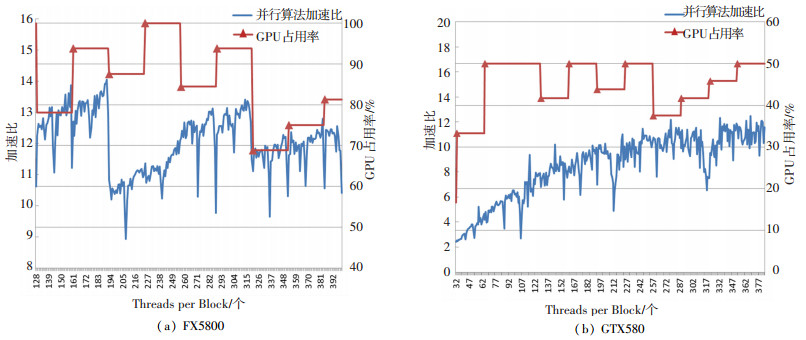
分别对基于GT200(计算核心1.3)和GF100(计算核心2.0)架构的FX5800和GTX580进行了测试.由式(2)可知, 影响GPU占用率的主要参数是Registers per Thread, SharedMemory per Block和Threads per Block.运行程序前, 在编译选项里面加入--ptxas-options=-v命令, 可以查看到本程序的Registers per Thread的值为42, SharedMemory per Block的值为1548字节.将参数代入式(2), 再调节Threads per Block的值, 就可以得到不同的GPU占用率, 如图 3所示.图 3(a)表明, 对于FX5800, GPU的占用率对加速比产生了较大影响.当Threads per Block为193时, GPU占用率从93.8%下降到87.5%, 而加速比也相应从14.1下降到了10.5.随后当Threads per Block的值为321时, 又再次出现了加速比随GPU占用率的降低而急速下降的情况.而图 3(b)表示, 对于GTX580而言, 这种关联并不明显, 这是由于GF100架构中新增加了高速缓存功能, 降低了访问冲突的发生.但仍可以发现, 几个加速比的低峰值, 均出现在GPU占用率较小的情况下.因此, 在分配线程时应选择合适的Threads per Block, 使得GPU的占用率足够大, 从而得到更好的加速比.
|
图 3 不同Threads per block下的GPU占用率和加速比 |
针对势能场方法提取骨架耗时长、计算复杂度高等问题, 提出了一种基于GPU的势能场骨架提取并行算法.由于在提取过程中势能场的计算占据了98%的时间, 对势能场的计算进行了并行性分析并提出并行算法, 另加入了CUDA架构特有的存储器结构对普通并行算法进行了优化.此外, 还讨论了如何根据显卡设备和程序的固有属性来分配线程以达到最高的GPU占用率, 从而得到最优的加速效果.实验结果表明, 当处理256×256×487规模的体数据时, 可以获得18倍的加速比, 有效地减少了骨架提取时间.
| [1] |
LIVESU M, SCATENI R. Extracting curve-skeletons from digital shapes using occluding contours[J]. The Visual computer, 2013, 29(9): 907-916. DOI:10.1007/s00371-013-0855-8 |
| [2] |
TAGLIASACCHI A, ALHASHIM I, OLSON M, et al. Mean Curvature Skeletons[J]. Computer Graphics Forum, 2012, 31: 1735-1744. DOI:10.1111/cgf.2012.31.issue-5 |
| [3] |
Zhang Q, SONG X, SHAO X, et al. Unsupervised skeleton extraction and motion capture from 3D deformable matching[J]. Neurocomputing, 2013, 100: 170-182. DOI:10.1016/j.neucom.2011.11.032 |
| [4] |
BERTRAND G, COUPRIE M. Powerful parallel and symmetric 3d thinning schemesbased on critical kernels[J]. J Math Imaging Vis, 2014, 48: 134-148. DOI:10.1007/s10851-012-0402-7 |
| [5] |
ARCELLI C, DI BAJA G S, SERINO L. Distance-driven skeletonization in voxel images[J]. IEEE Trans Pattern Anal Mach Intell, 2011, 33(4): 709-720. DOI:10.1109/TPAMI.2010.140 |
| [6] |
CORNEA ND, SILVER D, MIN P. Curve-skeleton properties, applications, and algorithms[J]. IEEE Transactions on Visualization and Computer Graphics, 2007, 13(3): 530-548. DOI:10.1109/TVCG.2007.1002 |
| [7] |
CORNEA N D, SILVER D, YUAN Xiaosong, et al. Computing hierarchical curve-skeletons of 3D objects[J]. The Visual Computer, 2005, 21(11): 945-955. DOI:10.1007/s00371-005-0308-0 |
| [8] |
LIU B, TELEA A C, ROERDINK J B T M, et al. Parallel centerline extraction on the GPU[J]. Computers & Graphics, 2014, 41: 72-83. |
| [9] |
LEE C, RO W W, GAUDIOT J L, et al. Boosting CUDA applications with CPU-GPU hybrid computing[J]. International Journal of Parallel Programming, 2014, 42(2): 384-404. DOI:10.1007/s10766-013-0252-y |
| [10] |
JIMÉNEZ J. Three-dimensional thinning algorithms on graphics processing units and multicore CPUs[J]. Concurrency and Computation:Practice and Experience, 2012, 24: 1551-1571. DOI:10.1002/cpe.v24.14 |
 2016, Vol. 48
2016, Vol. 48