2. 哈尔滨工业大学(威海) 信息工程研究所, 264209 山东 威海
2. School of Information Engineering, Harbin Institute of Technology at Weihai, 264209 Weihai, Shandong, China
波达方向DOA(Direction of arrival)估计是阵列信号处理研究的重要内容之一,在雷达、声呐、通信等领域有着广阔的应用前景.传统的MUSIC、ESPRIT等子空间类算法在信源独立或相关情况下具有良好的估计性能,但实际中广泛存在的多径传播及同频干扰使这些算法的估计性能急剧下降甚至失效.目前基于均匀线阵已有一些优良的解相干算法,如空间平滑算法[1-2]、矩阵重构类算法[3]等.但在工程应用中,均匀圆阵可提供360°方位信息,且不同方位上测向性能近似相同,应用更为广泛,因此基于均匀圆阵的解相干算法也成为关注的重点.在基于均匀圆阵模式变换类解相干算法中,文献[4]将平滑算法用于圆阵,提出基于模式空间变换的前后向平滑算法,但为适应通道噪声功率变化,需进行广义特征值分解来求取信号子空间;文献[5]将基于线阵的Toeplitz重构算法扩展到均匀圆阵,使信源协方差矩阵为对角阵,具有良好的解相干效果,但也由于仅用协方差矩阵一列进行重构,信息利用不充分,估计精度还有提升空间;文献[6-7]在均匀线阵差分算法[8-9]的基础上,提出基于均匀圆阵的差分Toeplitz重构算法,但差分方式需将独立、相关信号与相干信号分两次进行估计,并且在去掉独立信号时,相干信号的部分功率和信息也被减弱,影响了相干信号的DOA估计性能.
现有的基于圆阵模式空间变换的解相干算法都是以均匀线阵解相干算法为基础,通过算法的改进以适应模式变换引起的噪声变化.近年出现一种基于均匀线阵的矢量重构类解相干算法[10-12],通过对协方差矩阵特征分解预处理抑制噪声,对相干信源有着更好的估计性能,但是该算法不能直接用于模式空间变换后的虚拟线阵.为此,本文在考虑模式变换对噪声影响的基础上将该算法用于均匀圆阵,将对噪声的处理提至变换前,降低算法的复杂度.
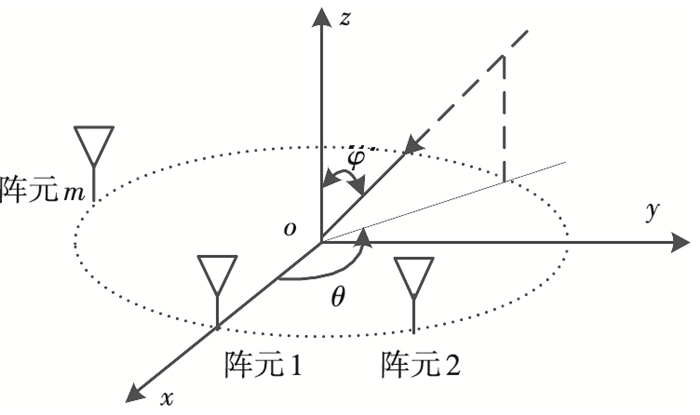
1 阵列信号模型及模式空间变换 1.1 信号接收模型与信号特征矢量如图 1所示,假设在xoy平面上有M个各向同性阵元,均匀排列于半径为r的圆周上,取圆心为参考点,信源的俯仰角φ∈[0, π/2]定义为入射方向与z轴之间的夹角,方位角θ∈[0, 2π)定义为入射方向在xoy平面上的投影与x轴在逆时针方向上的夹角.只讨论所有信源都与阵列共面的情形,即φ=π/2.
|
图 1 均匀圆阵的阵列模型 |
假设有N个波长为λ的远场窄带平面波信号入射至阵列,按相关性分为P组相互独立的相干信号,用pi表示第i组相干信源的信源个数,则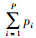
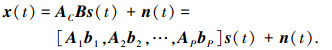
|
式中:x(t)


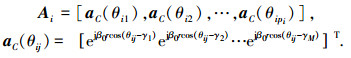
|
(1) |
式中,波数β0=2π/λ,阵列第m个阵元与x轴的夹角为γm=2π(m-1)/M,m=1, …, M.
由式(1)得M×M维均匀圆阵接收数据的协方差矩阵为
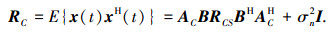
|
(2) |
式中,RCS=E{s(t)sH(t)}为P×P维信源的协方差矩阵,由信源假设可知rank(RCS)=P.对RC进行特征值分解:
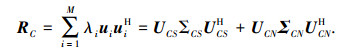
|
(3) |
式中:λ1≥λ2≥…λP>λP+1=…=λM=σn2为RC的特征值,且按从大到小排列,对应的特征矢量为u1, …, uM; ΣCS和ΣCN分别为前P个大特征值和后M-P个小特征值构成的对角阵;UCS=[u1, u2, …, uP]和UCN为相应的特征矢量矩阵.
1.2 模式空间变换由于均匀圆阵的阵列流型矩阵AC不具备范德蒙结构,需构造模式变换矩阵[4]将均匀圆阵输出进行变换.令
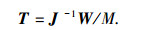
|
式中:J=diag{J-K(β0)/j-K, …, JK(β0)/jK},Jk(β0)表示k阶第1类贝塞尔函数,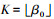
对均匀圆阵输出作模式变换得
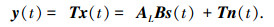
|
其中AL=TAC为模式变换后的虚拟阵列流型矩阵,且
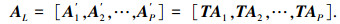
|
(4) |
式中,A′i=TAi为第i组相干信源L×pi维流型矩阵.其中L=2K+1表示变换后虚拟线阵的阵元数,当阵元数满足M>2K时

|
(5) |
由式(4)、(5)可知,经模式空间变换后的L×N维阵列流型矩阵AL具有范德蒙结构.变换后虚拟阵列数据协方差矩阵为
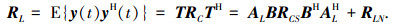
|
其中,变换后的噪声协方差矩阵为

|
(6) |
由式(6)可知RLN≠σn2I,模式变换使得虚拟线阵各通道的噪声功率不再相同,因此采用基于线阵的矢量重构解相干算法时,为获取均匀线阵的阵列流型空间,必须首先采用广义特征分解[4].
设λi和vi分别为矩阵束(RL, TTH)的广义特征值和特征矢量,广义特征值λ1~λL从大到小排列,前P个大广义特征值对应的特征矢量矩阵为ULS=[v1, …, vP], 可以证明(见附录):
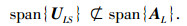
|
表明ULS张成的子空间不属于虚拟线阵导向矢量张成的信号子空间.因此,基于均匀线阵矢量重构算法若要用于虚拟线阵,还需进一步处理.令
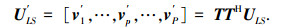
|
可以证明(见附录):

|
表明虚拟线阵导向矢量张成的信号子空间可由广义特征矢量矩阵ULS左乘TTH得到.记U′LS的第一列为v′1=[v′1, 1, v′2, 1, …, v′L, 1]T,将其按下式构造矩阵[8]:
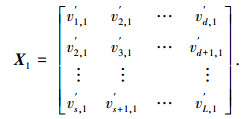
|
(7) |
式中,s=L-d+1,且d>N,s>N.进一步由矩阵X1进行反向特征矢量修正,得到s×2d维矩阵为
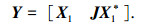
|
(8) |
其中,Js为s阶反对角线为1的置换矩阵.将Y与其共轭YH相乘,得
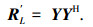
|
(9) |
对协方差矩阵R′L特征值分解构造MUSIC空间谱函数,通过谱峰搜索完成DOA估计.为方便描述,称此改进算法为MGEVD(Mode excitation GEVD)算法.
2.2 EMEVD算法由MGEVD算法原理知,算法由RC经TRCTH得到RL,通过对矩阵束(RL, TTH)进行广义特征分解得到广义特征矢量v1,对其左乘TTH得到用于解相干DOA估计的信号空间矢量v′1,算法复杂度较大(见表 1).为降低算法复杂度,证明了(见附录)
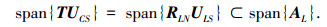
|
| 表 1 MGEVD算法和EMEVD算法运算量对比 |
即虚拟线阵导向矢量张成的信号子空间也可由均匀圆阵特征矢量矩阵UCS左乘T得到,在此基础上进一步改进,构造
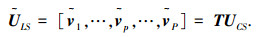
|
(10) |
取U′LS的第一列,并表示为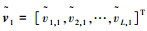
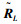
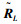
实际上,由附录的理论证明可知,2种改进算法由span{RLNULS}和span{TUCS}分别构造的信号子空间是等价的,但二者计算复杂度明显不同.
EMEVD算法利用UCS构造信号子空间, 只需先对RC进行特征分解提取最大信号特征矢量u1,并左乘T修正得到用于解相干DOA估计的特征矢量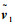
表 1中,GEVD(RL, TTH)→v1表示对矩阵束(RL, TTH)求解最大广义特征矢量v1,EVD(RC)→u1表示对RC求解最大特征矢量u1,二者的复杂度均采用快速子空间分解技术[13],则前2种算法在MUSIC谱峰搜索前的总运算量为
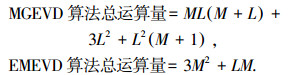
|
一般取,假设M=L+4=19,则
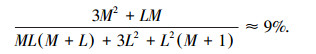
|
可见运算量显著降低.
2.3 算法流程EMEVD算法流程如下:
1) 记录D个快拍下阵列输出信号矢量x(t),t=1, 2, …, D;
2) 由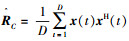
3) 将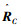
4) 由式(10)得变换后最大特征矢量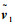
5) 对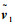
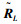
6) 将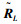
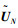
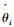
仿真实验对比了EMEVD算法和MGEVD算法的空间谱,并将EMEVD算法与目前基于均匀圆阵模式空间变换的解相干算法MODE-FBSS[4]、MODE-TOEP[5]、MODE-DIFF-TOEP[6]进行比较.
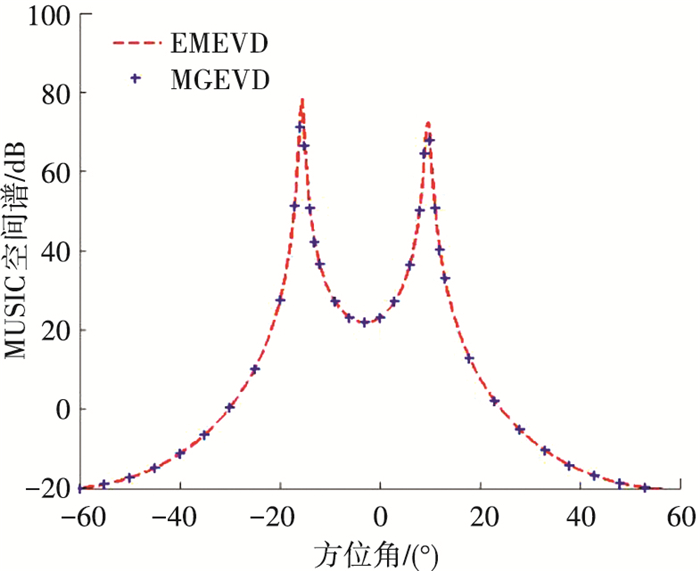
实验1 EMEVD和MGEVD算法的空间谱图.设2个方位角为(-15°,10°)的等功率全相干信号,信噪比为20 dB,快拍数为200,采用19个阵元的均匀圆阵,阵元半径为3.52λ/π,模式变换后虚拟线阵的阵元数为15,取2种算法的子阵阶数为8,2种算法空间谱比较如图 2所示.
|
图 2 EMEVD和MGEVD的空间谱比较 |
由图 2可见,2种算法空间谱重合,验证了MGEVD、EMEVD算法分别由span{RLNULS}和span{TUCS}构造信号子空间等价的结论.
实验2 4种算法的DOA估计均方误差、成功分辨率与信噪比的关系.设4个等功率信号,第1组方位角为(-43°, -26°)的全相干信号,后2组方位角分别为30°和55°的独立信号,快拍数固定为256.实验中,估计均方误差的公式采用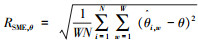
|
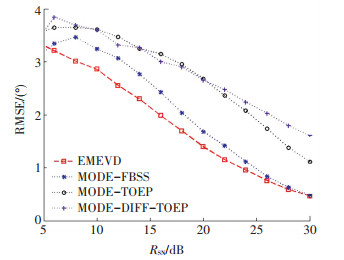
图 3 RMSE随RSN变化的关系曲线 |

|
图 4 成功分辨率随RSN变化的关系曲线 |
由图 3和图 4可见,4种算法的估计精度和成功分辨率曲线都随RSN增加而提高.图 3表明在低信噪比下,EMEVD的估计精度和成功分辨率明显高于其他3种算法,随着RSN的增加,EMEVD与MODE-FBSS均方误差性能接近,在高信噪比下,EMEVD的估计精度略优于MODE-FBSS,但它们的估计精度均优于MODE-TOEP和MODE-DIFF-TOEP.图 4表明EMEVD具有较高的成功分辨率且信噪比门限更低.
实验3 4种算法的DOA估计均方误差、成功分辨率与快拍数的关系. RSN固定为20 dB,每个快拍数进行2 000次Monte-Carlo实验,其它仿真参数同实验1. RSME和成功分辨随快拍数变化的关系如图 5、图 6所示.

|
图 5 RSME随快拍数变化的关系曲线 |
|
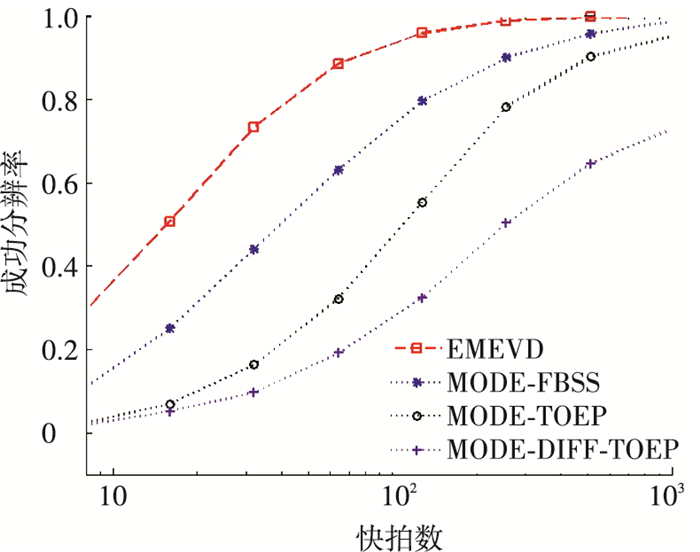
图 6 成功分辨率随快拍数变化的关系曲线 |
由图 5和图 6可见,4种算法的DOA估计精度和分辨率随快拍数增加而提高.图 5表明EMEVD的估计精度在不同快拍数下均优于其他3种算法;EMEVD和MODE-FBSS的估计精度随快拍数增加改善较大,在大快拍数下二者精度都较高,而MODE-TOEP和MODE-DIFF-TOEP的估计精度随着快拍数的增加变化较慢,精度略低.图 6表明EMEVD分辨率随快拍数增加而提高,且明显高于其他3种算法.
4 结论在考虑模式变换引起噪声功率变化的基础上,通过分析广义特征矢量与虚拟线阵信号空间的关系,对矢量重构解相干算法加以改进,提出适用于均匀圆阵模式变换的MGEVD算法.针对该算法计算复杂度高的问题提出改进的EMEVD算法,将模式空间变换后的相关处理步骤提前到模式变换前, 其性能估计的实质不变, 但计算量和复杂度大大降低.
理论分析与仿真实验表明,EMEVD矢量重构类算法估计精度较高, 然而算法高估计精度的代价是比已有的MODE-FBSS、MODE-TOEP和MODE-DIFF-TOEP等算法需多进行一次特征值分解, 因此如何进一步降低两次特征值分解的计算量值得今后研究.
附录定理1[3] 假设N(N≤M-1)个窄带远场信号入射到M个阵元组成的阵列上,接收数据的协方差矩阵为
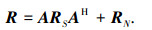
|
式中:A=[a1, …, an, …, aN]为阵列流型矩阵,RS为信号协方差矩阵,RN为噪声协方差矩阵.假设N个信号可以分为P组组间独立、组内相干的信号,由信源假设条件可知rank(RS)=P,P≤N.设up为矩阵束(R, RN)的第p个大广义特征值对应的特征矢量,存在如下线性关系:
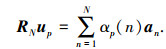
|
(11) |
其中,αp(n)为线性组合因子,1≤p≤P.
式(11)说明无论信号源是否相干,RNup是信号源导向矢量的一个线性组合,且包含了信号的全部信息,基于此可以进行解相干处理.若令广义特征矢量矩阵US=[u1, …, up, …, uP],由定理1可得到如下推论:
推论1 若RN≠σn2I,US为矩阵束(R, RN)的广义特征矢量矩阵,则
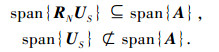
|
(12) |
推论2 若RN=σn2I,US退化为矩阵R的特征矢量矩阵,则

|
(13) |
当P=N时,式(12)、(13)等号成立.
由推论2可知,均匀圆阵的矢量矩阵UCS和导向矢量矩阵AC所张成的信号子空间之间的关系为
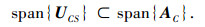
|
(14) |
且模式变换后虚拟均匀线阵的信号子空间为
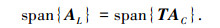
|
(15) |
结合式(14)、(15)可得
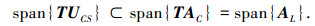
|
(16) |
由推论1可知
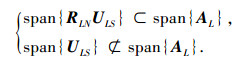
|
(17) |
式(16)、(17)表明,子空间span{AL}包含子空间span{TUCS}和span{RLNULS}.
可以证明
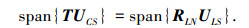
|
证明 设up为均匀圆阵前P个大特征矢量中第p列特征矢量,令矢量vp=(TH)-up,则
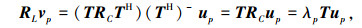
|
(18) |
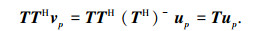
|
(19) |
联立式(18)和(19),得
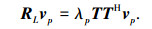
|
由此可知,λp和vp为矩阵束(RL, TTH)的前P个大特征矢量中第p个广义特征值和对应的特征矢量,且
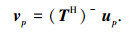
|
(20) |
再依据式(6)、(20),得
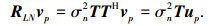
|
(21) |
由式(21)可得
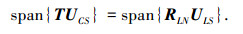
|
证毕.
| [1] |
SHAN Tiejun, WAX M, KAILATH T. On spatial smoothing for direction-of-arrival estimation of coherent signals[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1985, 33(4): 806-811. DOI:10.1109/TASSP.1985.1164649 |
| [2] |
PILLAI S U, KWON B H. Forward/backward spatial smoothing techniques for coherent signal identification[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1989, 37(1): 8-15. DOI:10.1109/29.17496 |
| [3] |
CADZOW J A, KIM Y S, SHIUE D C. General direction-of-arrival estimation:a signal subspace approach[J]. IEEE Transactions on Aerospace and Electronic Systems, 1989, 25(1): 31-47. DOI:10.1109/7.18659 |
| [4] |
WAX M, SHEINVALD J. Direction finding of coherent signals via spatial smoothing for uniform circular arrays[J]. IEEE Transactions on Antennas and Propagation, 1994, 42(5): 613-620. DOI:10.1109/8.299559 |
| [5] |
高书彦, 陈辉, 王永良, 等. 基于均匀圆阵的模式空间矩阵重构算法[J]. 电子与信息学报, 2007, 29(12): 2832-2835. |
| [6] |
谢菊兰, 李会勇, 何子述. 均匀圆阵相干信源DOA估计的差分算法[J]. 电子科技大学学报, 2012, 41(4): 516-521. |
| [7] |
甄佳奇, 丁群, 赵冰. 虚拟阵列下的相干信号测向算法[J]. 系统工程与电子技术, 2013, 35(10): 2032-2036. DOI:10.3969/j.issn.1001-506X.2013.10.03 |
| [8] |
YE Zhongfu, XU Xu. DOA estimation by exploiting the symmetric configuration of uniform linear array[J]. IEEE Transactions on Antennas and Propagation, 2007, 55(12): 3716-3720. DOI:10.1109/TAP.2007.910493 |
| [9] |
LIU Fulai, WANG Jinkuan, SUN Changyin, et al. Spatial differencing method for DOA estimation under the coexistence of both uncorrelated and coherent signals[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(4): 2052-2062. DOI:10.1109/TAP.2012.2186216 |
| [10] |
胡晓琴, 陈辉, 陈建文, 等. 一种利用最大特征矢量的Toeplitz去相干方法[J]. 电子学报, 2008, 36(9): 1710-1714. |
| [11] |
CHOI Y H. ESPRIT-based coherent source localization with forward and backward vectors[J]. IEEE Transactions on Signal Processing, 2010, 58(12): 6416-6420. DOI:10.1109/TSP.2010.2077634 |
| [12] |
刁鸣, 安春莲. 基于矢量重构的相干信源测向[J]. 应用科学学报, 2011, 29(3): 261-266. |
| [13] |
XU Guanghan, KAILATH T. Fast subspace decomposition[J]. IEEE Transactions on Signal Processing, 1994, 42(3): 539-551. DOI:10.1109/78.277846 |
 2016, Vol. 48
2016, Vol. 48



