近年来,随着3D电影的风靡和3D电视的推出,3D产品已成为一种大众消费品.但是,由于不同屏幕的光学特性不同,立体图像在不同的显示屏幕上的显示效果也不相同.在小屏幕显示时观看者感觉舒适的图像,在大屏幕显示时,观看者会出现不舒适的感觉甚至出现复视现象.因此针对不同显示设备的立体内容调整研究是目前立体显示领域的一个研究热点.
解决这种立体视觉差异的最佳方法是调节立体内容的深度以适应不同屏幕的光学特性,而调节深度可通过调整立体图像的视差范围实现.文献[1-2]研究用手动方式为特定显示器调整立体图像视差的方法.但这些方法的调整方案仅靠感官判断,没有公式化的调整原则.文献[3-5]研究基于图像的视图差补方法,如摄像机标定和深度图校正,这些方法需要大量复杂的计算.文献[6]提出一种调整左右眼图像在原立体图像中相对位置的方法,该方法实现了视差调节且操作简单,但是该方法假设原立体图像不存在垂直视差,因此对存在垂直视差的立体图像无法实现垂直视差的调整.
本文提出一种使获取的立体图像在显示设备上舒适显示的线性调整方法,可给观看者提供舒适的观看体验.首先利用立体图像融像区的知识[7],得到不同显示器舒适显示的视差范围;然后利用匹配的SIFT(scale-invariant features) [8]特征点来估计获取的立体图像的视差范围,建立起立体图像视差到舒适显示视差的线性映射,满足特定立体显示设备舒适显示的需要;最后利用奇异值分解的方法估计投影变换矩阵,实现对立体图像垂直和水平视差的调整.
1 立体视觉及图像变换 1.1 立体图像融像区观看者观看立体图像时,双眼聚焦于立体屏幕上,使大脑认为观看距离为S, 而立体图像视差信息暗示观看物体的距离为S′.当水平视差太大时,S与S′间的差值超过阈值,观看者将无法在大脑中融合左右眼图像,感受不到立体视觉效果.这一现象由文献[9]首先发现,并将在注视点周围可以形成单像的区域称为立体图像融像区.融像区内的物体均能在大脑中融合,融像区外的物体会形成双眼复视并造成视觉疲劳.如果立体图像还存在垂直视差,那么融合图像的边缘将出现畸变,加剧观看者的疲劳程度.因此需要将左右眼图像的水平视差控制在一定范围内,同时消除垂直视差.
文献[6]给出可使观看者舒适观看立体图像的水平像素差应满足的条件:

|
(1) |
式中:Δn为左右视点图像的水平像素差; S为观看距离; Pw为显示屏像素宽度; D为瞳孔直径,通常为4 mm; η≈2.907×10-4rad为人眼视锐度; Ee为观看者瞳距, 通常为6.5 cm.
1.2 图像变换与特征点提取通过确定调整前后图像中特征点的坐标,计算线性变换模型中的变换矩阵M
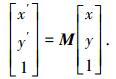
|
(2) |
式中: (x, y)为原始图像中点的坐标,(x′, y′)为变换后图像中对应点的坐标.而
为实现左右视点图像的调整,必须得到图像的水平视差与垂直视差以确定式(2)中变换后的坐标.首先需要完成立体图像的匹配[10-11],寻找合适的特征点计算上述两种视差.
本文采用SIFT特征点检测算法提取图像特征点,该算法运算速度较快且稳定性好,在图像处理领域具有深入广泛的应用[12-13].计算左右眼图像中SIFT特征点的特征向量欧式距离即可实现特征点匹配.
2 立体图像视差调整算法 2.1 垂直视差调整设左右眼图像ILIR通过SIFT算法获得的匹配特征点坐标分别为PiL=(xiL, yiL),PiR=(xiR, yiR),两图像分别经过变换矩阵MLMR变换后,匹配特征点坐标变为PiL′=(xiL′, yiL′),PiR′=(xiR′, yiR′).代入式(2),有

|
(3) |
垂直视差调整就是要将左右眼图像中的垂直像素差调整为0,即Δyi=0,令左眼图像IL为参考图像,右眼图像IR为待调整图像,则

|
(4) |
即令IL中特征点纵坐标在变换后保持不变,而IR中特征点纵坐标在变换后则与左视点相同,从而达到消除垂直视差的目的.
将式(4)代入式(3)得

|
(5) |
式中xiL′, xiR′为待定量.
2.2 水平视差调整进行水平视差调整时,首先应确定左右眼图像间的水平像素差.利用SIFT算法寻找到匹配特征点PiL, PiR的横坐标xiL, xiR.由于获得的匹配特征点可能存在误匹配的情况,而这些误匹配点的水平像素差通常与正确的匹配点水平像素差之间差别较大.利用直方图统计水平像素差可排除存在的误匹配点,得到较为准确的水平像素差信息.具体方法如下:
1) 计算匹配特征点之间的水平像素差di,即
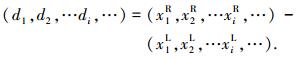
|
2) 对di进行直方图统计,组距为1个水平像素,计算统计直方图中所有统计点个数,记为Ptotal;计算统计直方图中视差值最大的5组数据中统计点的个数,记为Pmax.
3) 计算Pmax/Ptotal并将它与给定的阈值T%进行比较,若小于给定的阈值,则认为当前统计直方图中的dmax数据是由不具有典型性的匹配特征点提供的,因此从匹配特征点中删除这些点并重复步骤3;若大于给定阈值,则认为当前统计直方图中的dmax即为该立体图像的最大水平像素差.
实验中阈值T%通常取5%~10%即可滤除明显的误匹配点.
使用类似的方法可以获得最小水平像素差dmin.最终确定的立体图像的水平像素差范围为[dmin, dmax].
另一方面,立体图像的水平视差在不超过式(1)所定义的水平视差Δn时,观看者可得到舒适的立体图像.令dm=(ηSEe)/(DPw),则舒适观看的水平像素差区间Δn为[-dm, dm].
当立体图像的水平像素差过大时,应该减小水平像素差,使其处于区间Δn的范围内,另一方面,当水平像素差过小时,会存在立体效果不明显的问题,因此可以适当增大水平像素差.进行如图 1所示的映射,使调整后水平像素差满足

|
图 1 水平视差调整的映射关系 |
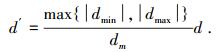
|
(6) |
式中:d为调整前水平像素差,d′为调整后水平像素差.该式中调整前后0视差平面保持不变,并把调整后的水平像素差约束在区间Δn的范围内.
令|d|max=max{|dmin|, |dmax|},若|d|max>dm, 则立体图像的水平视差过大,需要缩小水平视差.由于仅对单张图像进行视差调整可能使调整后图像存在过大的形变,因此本文同时对左右眼图像进行调整,即左视点图像中的特征点PiL向右移动di(1-dm/|d|max)/2个像素,右视点图像中的特征点PiR向左移动di(1-dm/|d|max)/2个像素.
同理,当|d|max < dm,应扩大水平视差,即左视点图像中的特征点PiL向左移动di(dm/|d|max-1)/2个像素,右视点图像中的特征点PiR向右移动di(dm/|d|max-1)/2个像素.
可得到水平视差调整后左右视点图像的匹配特征点坐标与原特征点坐标关系如下:

|
(7) |
将式(7)代入式(5)得
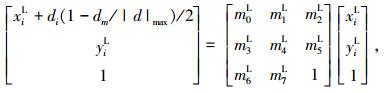
|
(8) |

|
(9) |
展开式(8)、(9)可得到方程组:
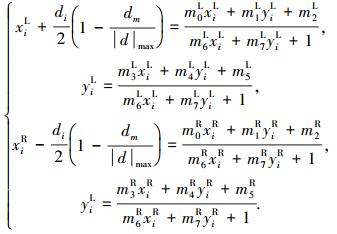
|
(10) |
式中:i取1~4,因此共存在16个等式.展开后化作矩阵形式,可利用奇异值分解并结合RANSAC算法[14-15]求出左右视点图像的变换矩阵ML,MR.当匹配特征点数量众多时,RANSAC算法可寻找出使可能多的特征匹配点满足变换的最佳变换矩阵.利用式(2)及变换矩阵即可获得视差调整后的左右视点立体图像.
3 实验为检验本文提出的视差调整算法,分别选择两幅视差过大和两幅视差过小的立体图像进行视差调整,且这4幅图像中均存在一定的垂直视差.播放立体图像的屏幕为分辨率1 920×1 080的24英寸显示屏,观看距离为1.5 m.根据显示屏尺寸与分辨率显示屏像素宽度为

|
(11) |
式中: l为显示屏尺寸,w×h为屏幕分辨率.再结合式(1)可算得该显示屏舒适观看的水平像素差Δn=[-26, 26].
立体图像视差调整过程见图 2. 图 2中(g)~(k)为(a)~(c)、(e)、(f)部分放大后的图. 图 2(a)为原立体图像左视点图,图 2(b)为利用SIFT算法寻找到的匹配特征点所作的左视点的所有特征点及其视差(线条两端点表示特征点在左右视点的位置),其中存在本文提及的误匹配特征点.用本文提出的检测算法排除误匹配点后得到匹配特征点图 2(c).将图 2(c)中的特征点的最大视差作为估计的最大视差,根据之前视差调整方法,建立原始立体图像视差与目标视差之间的映射关系,如图 2(d)所示.根据式(10),求得变换矩阵,并应用到左右视点中,得到最后的图像图 2(e)、(f)为合成后的立体图像,对比图 2(i)、(j),蓝色连线变短,即视差变小,取得了很好的调整效果.由于匹配特征点太多,为更好展示调整过程,在放大图中,只展示部分匹配特征点.
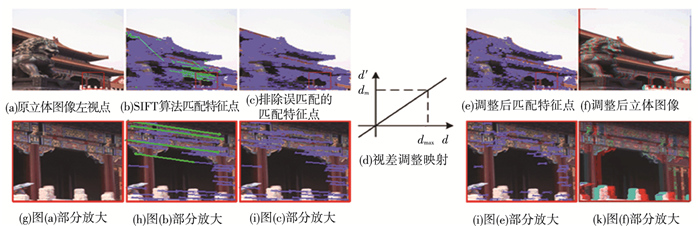
|
图 2 视差调整过程 |
图 3中调整前的立体图像(a)“铜狮”、(b)“校门”水平视差均过大,都具有明显垂直视差.经过视差调整后得到的(c)“铜狮”、(d)“校门”消除了垂直视差,且水平视差减小到舒适观看的范围. 图 4中调整前的(a)“雕像”水平视差太小,观看时立体效果不明显,且具有明显的垂直视差,调整前的(b)“故宫”垂直视差很大,直接观看时图内景物边缘处发生畸变.经过视差调整后的(c)“雕像”、(d)“故宫”都成功消除了垂直视差,且在舒适观看的范围内尽量增大了水平视差,使调整后图像有了更好的立体效果.

|
图 3 水平视差过大的立体图像的调整 |

|
图 4 水平视差过小的立体图像的调整 |
将本文算法与文献[9]所述算法进行比较,进一步验证本文算法的视差调整效果.以前面实验中的“铜狮”“故宫”为例,对比结果见图 5. “铜狮”立体图像视差过大,2种算法都成功将图像调整至立体图像融像区的范围,但是文献[9]的算法将原来一部分视差明显的图像区域的视差调整至0,调整后该部分区域立体效果减弱. “故宫”的视差在立体图像融像区范围内,但是立体效果不够明显.文献[9]的算法认为该图像不需要调整,因此未对该图像的视差进行调整,本文算法在融像区允许的范围内对立体图像视差进行了增大操作,使调整后的立体图像仍能舒适显示并且立体效果更为明显.另外,由于文献[9]的算法为考虑立体图像中存在垂直视差的问题,因此2幅图像调整后仍能观察到垂直视差.

|
图 5 算法比较 |
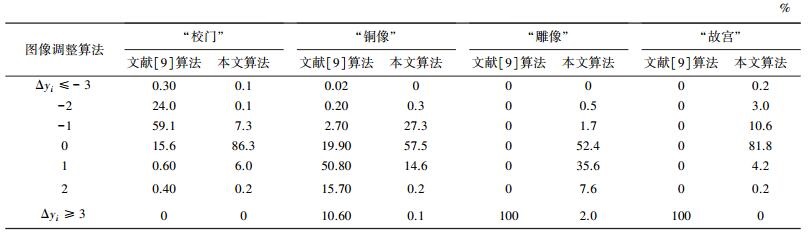
表 1统计了“校门”“铜像”“雕像”“故宫”4幅图像根据文献[9]所述算法与本文算法调整立体图像后垂直像素差Δyi的分部情况.从表 1中可看出,文献[9]所述的算法并没有很好的考虑垂直视差的问题.当立体图像存在垂直视差时,文献[9]的算法并不能很好的对垂直视差进行处理,调整完成的图片仍可能存在较大的垂直视差.而立体图像经过本文提出的算法调整后,垂直视差都得到很大的改善. 表 1中4幅图像经过本文算法调整后垂直像素差都基本可控制在[-2, 2]的范围内,很好地消除了垂直视差.
| 表 1 垂直像素差统计 |
双视点设备获取的立体图像很难直接应用于显示设备.当立体图像具有垂直视差或者相对于指定的屏幕水平视差过大或者过小时, 都会给观看者带来视觉体验上的问题.因此立体设备获取的双目立体图像必须经过图像调整的处理方法来实现立体图像在指定屏幕上的舒适显示.
本文提出一种基于特征点匹配的立体视差矫正算法,该算法建立起从立体图像原有视差到舒适显示视差的线性映射,并利用奇异值分解的方法计算出该映射的投影变换矩阵,从而实现对立体图像垂直视差和水平视差的调整.实验结果表明,该算法具有很好的显示效果,并保证了双目立体图像的一致性.
| [1] |
FELDMANN I, SCHREER O, KAUFF P. Navigation dependent nonlinear depth scaling[C]//Picture Coding Symposium. Saint Malo, France: INRIA, 2003: 387-390. http://www.researchgate.net/publication/228548964_Navigation_Dependent_Nonlinear_Depth_Scaling
|
| [2] |
WANG C, SAWCHUK A A. Disparity manipulation for stereo images and video[C]//Stereoscopic Displays and Applications XIX. San Jose, CA: SPIE, 2008: 68031E-68031E-12. http://spie.org/Publications/Proceedings/Paper/10.1117/12.767702
|
| [3] |
KIM M, LEE S, CHOI C, et al. Depth scaling of multiview images for automultiscopic 3D monitors[C]//20083DTV-Conference: The True Vision-Capture, Transmission and Display of 3D Video. Istanbul. Turkey: IEEE, 2008: 181-184. http://ieeexplore.ieee.org/document/4547838/
|
| [4] |
SMOLIC A, MULLER K, DIX K, et al. Intermediate view interpolation based on multiview video plus depth for advanced 3D video systems[C]//ICIP 2008. San Diego, CA: IEEE, 2008: 2448-2451.
|
| [5] |
BLEYER M, GELAUTZ M, ROTHER C, et al. A stereo approach that handles the matting problem via image warping[C]//IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Miami, FL: IEEE, 2009: 501-508. http://doi.ieeecomputersociety.org/10.1109/CVPRW.2009.5206656
|
| [6] |
张丞, 侯春萍, 王晓燕. 立体图像视差自适应调整算法[J]. 光电子激光, 2014, 25(3): 581-587. |
| [7] |
MAXWELL M G. Three-dimensional color television[J]. SMPTE journal, 1985, 94(8): 821-825. DOI:10.5594/J03398 |
| [8] |
LOWE D G. Object recognition from local scale-invariant features[C]//Proceedings of the Seventh IEEE International Conference on Computer Vision. Los Alamitos, CA: IEEE, 1999, 2: 1150-1157.
|
| [9] |
PANUM P L. Physiologische Untersuchungen über das Sehen mit zwei Augen[M]. Charleston, SC: Nabu Press, 2010.
|
| [10] |
王华, 丛建亭, 侯相深, 等. 畸变图像的有效配准算法[J]. 哈尔滨工业大学学报, 2010, 42(4): 597-601. DOI:10.11918/j.issn.0367-6234.2010.04.020 |
| [11] |
王磊, 张钧萍, 张晔. 基于特征的SAR图像与光学图像自动配准[J]. 哈尔滨工业大学学报, 2005, 37(1): 22-25. |
| [12] |
LI J, LU Z. B-SIFT: a highly efficient binary SIFT descriptor for invariant feature correspondence[C]//2nd Sino-Foreign-Interchange Workshop on Intelligent Science and Intelligent Data Engineering, IScIDE 2011. Xi'an: Springer Berlin Heidelberg, 2012: 426-433. http://www.springerlink.com/content/ql04371wm4161878/
|
| [13] |
SOYEL H, DEMIREL H. Improved SIFT matching for pose robust facial expression recognition[C]//2011 IEEE International Conference on Automatic Face & Gesture Recognition (FG 2011). Santa Barbara, CA: IEEE, 2011: 585-590. http://ieeexplore.ieee.org/document/5771463/
|
| [14] |
HARTLEY R, ZISSERMAN A. Multiple view geometry in computer vision[M]. Cambridge: Cambridge university press, 2003.
|
| [15] |
SATTLER T, LEIBE B, KOBBELT L. SCRAMSAC: Improving RANSAC's efficiency with a spatial consistency filter[C]//2009 IEEE 12th International Conference on Computer Vision. Kyoto: IEEE, 2009: 2090-2097. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=5459459
|
 2016, Vol. 48
2016, Vol. 48