ETFE膜结构常作为建筑屋面或立面而应用于体育馆、体育场、展览馆、温室等土木工程领域.1982年,ETFE膜结构首次建成于荷兰,随后在气候温和的西欧迅速发展,特别是在德国、英国等,再逐渐发展到世界各地[1].2008年北京奥运会,ETFE膜结构进入中国,水立方和鸟巢是代表作.2010年上海世博会,中德生态馆和日本馆是ETFE膜结构.
ETFE膜结构常以气枕的形式应用于建筑中[1, 2].根据裁切模型的不同,ETFE气枕成形设计方法有三维裁切和平面裁切两种.三维裁切方法又可细分为基于找形后的形态和找形分析零应力态两种,两者均经过找形、结构分析、裁切等阶段,膜材裁片为曲边,焊接为曲面.工程中常用的三维裁切方法,基于找形后的形态进行裁切和结构分析,并考虑一致性的应变补偿[1],但会导致分析与实际的外形和应力不一致,而基于找形分析零应力态的三维裁切方法能够很好地解决这个问题.三维裁切方法裁切、焊接效率低,耗材高,但可适用于任意气枕,特别是矢高较大的气枕.平面裁切方法,通过简单的平面裁切和焊接来形成气枕结构,再通过充气成形使ETFE材料产生合理的徐变和强化[3, 4, 5, 6],得到理想的初始曲面形态;该方法具有裁切、焊接简单,易于安装,经济等优点.
针对ETFE气枕结构,国内外不少学者进行过相关理论分析与试验研究.傅学怡等[7, 8]介绍了北京奥运国家游泳中心结构的设计;吴明儿等[9, 10]进行了ETFE气枕的设计与结构试验,并提出了弹簧支撑的枕式结构;顾磊等[11]进行了ETFE气枕分析和模型试验;杨庆山等[12, 13]对ETFE气枕模型进行了力学性能试验及有限元分析;陈务军等[14, 15, 16, 17]对ETFE薄膜材料力学性能、气枕结构设计分析理论和气枕模型试验进行了较深入的研究,建立了充气膜零应力态理论,并采用三维扫描仪进行了测试验证,对ETFE气枕集成光伏电池系统进行了试验研究.但是,较少有文献对ETFE气枕结构的成形设计方法进行公开报道.
本文引入基于找形分析零应力态的三维裁切和基于材料非线性的平面裁切两种设计方法,对比了两种方法的设计过程,并分别分析了相应的设计分析全过程和力学模型.通过两个ETFE气枕模型的充气成形试验和数值模拟,得到了结构的膜面外形和应力分布及其变化规律,验证了提出的成形设计方法.
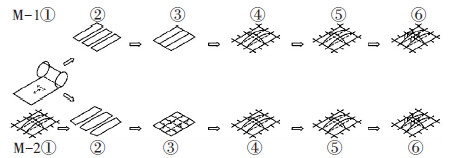
1 ETFE气枕成形设计方法 1.1 成形设计方法本文引入基于找形分析零应力态的三维裁切和基于材料非线性的平面裁切两种成形设计方法,图 1所示为两种设计方法与设计过程. M-1为基于平面裁切的方法,其中①为建筑设计概念,②为平面裁切片,③为平面焊接,④为充气成形并保留合理残余变形,⑤为现场安装,⑥为气枕工作并承受外载.M-2为基于三维裁切的方法,其中①为解析零应力态,②为曲边裁切片,③为曲面焊接,④为充气检漏,⑤为现场安装,⑥为气枕工作并承受外载.
|
图1 ETFE气枕成形设计方法与设计过程 |
M-1的难点在于利用ETFE薄膜的材料非线性,对气枕进行充气成形,使膜面应力进入塑性阶段,薄膜材料产生足够的残余应变来得到理想的初始形态.相对而言,M-2的难点在于零应力态的求解.
1.2 设计与分析过程 1.2.1 平面裁切平面裁切的方法,通过对气枕进行充气成形,使ETFE薄膜产生合理的徐变,得到理想的初始曲面形态.因此,ETFE薄膜的力学性能是实现平面载切方法的基础.ETFE薄膜的单向拉伸性能呈现非线性,具有两个明显的屈服点,在常温且小于第一屈服点下具有较好的弹性特性[3, 4].ETFE薄膜受到长时间拉伸时会产生较为显著的徐变,将力卸载以后,有明显的徐变恢复过程,但是变形并不能完全恢复,会留有残余变形,其大小与拉力、时间、温度密切相关[5, 6].
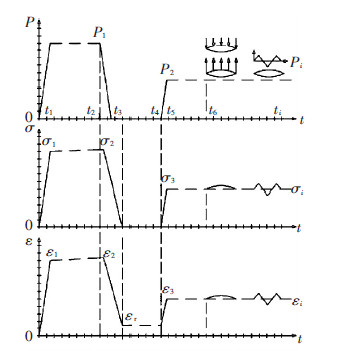
图 2为基于平面裁切的ETFE气枕设计过程的状态和力学模型.0~t3为充气成形,并细分0~t1为充气加压、t1~t2为保压、t2~t3为放气泄压,根据设计情况此过程可重复1~2次;t3~ t4为零压,存放、转运、安装阶段;t4~t5为现场安装;t5~t6为充气预张力态;t6~ti为恒载、风载等外载荷作用阶段.ETFE气枕的应力特征,具有与充气一致的时间度量,但呈现时滞特性;应变特征也存时滞,与ETFE薄膜材料的单向徐变与恢复曲线相一致[5],在应力释放完之后仍有残余应变,该应变值决定了气枕工作的基本矢高.
|
图2 ETFE气枕平面裁切方法设计过程状态及力学模型 |
三维裁切方法,经过找形、结构分析、裁切等阶段,得到理想的初始曲面.工程中常用的三维裁切方法是基于找形后的形态,将弹性平衡态作为无应力态并重新施加预应力,将真实的材料属性赋予单元以后会发生形态“漂移”与预应力松驰,导致分析与实际的外形和应力不一致.对于一般项目,这一差异可忽略,但对大型工程项目或者对精度要求较高的项目就无法忽略这个问题[1, 15].
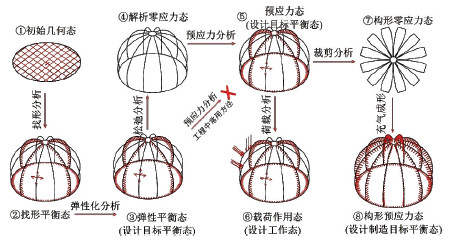
图 3为基于找形分析零应力态三维裁切的ETFE气枕设计方法分析过程状态.由初始几何形态①,根据充气压力和膜面应力进行找形分析,得到找形平衡态②,再经过弹性化分析后,可得到弹性平衡态③.为得到理想的构形预应力态⑧,弹性平衡态③经过逆解析或松弛分析后,得到解析零应力态④.在解析零应力态④下进行裁剪分析,得到构形零应力态⑦,可防止结构充气成形时的构形预应力态⑧与设计目标形态⑤产生误差[14, 15].荷载分析在预应力态⑤的基础上进行,可得到结构的荷载作用态⑥.工程常用的方法是将弹性平衡态③通过预应力分析直接得到预应力态⑤,会导致明显偏差[1, 15].
|
图3 ETFE气枕三维裁切方法分析过程状态 |
气枕的初始几何为边长1.5 m的正方形,根据目标内压3.5 kPa及膜面应力10 MPa,可得到气枕的找形平衡态,再经过弹性化分析后得到弹性平衡态.基于充气膜零应力态理论[14],将气枕的弹性平衡态经逆解析得到解析零应力态.基于解析零应力态,可以对模型进行预应力分析、荷载分析和裁切分析.
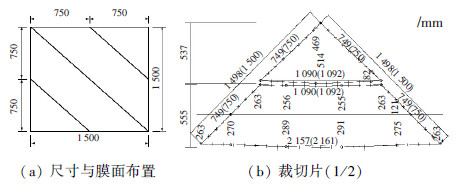
2.1.2 裁切分析基于解析零应力态,对三维模型进行裁切分析,得到构形零应力态,即膜材裁片,见图 4.双层膜面对称地设有三道热合焊缝,膜片经275度高温热合焊接而成.气枕边缘处也采用热合加工,并包裹直径6 mm的PE棒,然后利用铝合金夹具通过螺栓固定于钢框架上.
|
图4 ETFE气枕尺寸与裁切片(三维裁切) |
首先进行准备工作:在气枕外膜面按网格粘贴靶点,架设三维扫描仪,压力控制系统通过外膜面预留的两个配有密封性能的气门芯进行接入.试验系统见图 5.利用压力控制系统对ETFE气枕进行充气加压至3.5 kPa.在试验过程中,利用三维扫描仪对外膜面整体外形进行测量,ETFE气枕内部压力由压力控制系统自动记录.

|
图5 ETFE气枕试验系统(三维裁切) |
基于三维扫描仪测量得到的外形,应用引入线性调整理论的力密度法,结合实际测得的气枕内压及边界条件,可计算得到不同内压下的膜面应力分布[18, 19].对三维裁切成形模型进行数值模拟,可得到相应的膜面外形、应力分布及其变化规律.
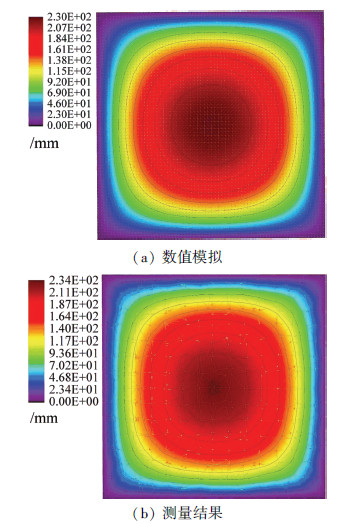
ETFE气枕的膜面外形是建筑设计概念的表现形式,正方形ETFE气枕在3.5 kPa下的膜面外形见图 6.试验结果与数值模拟相比,可发现两者的变化规律高度一致,具有相同的层次和变化梯度;不同的是,两者存在误差,其最大误差为4 mm,试验结果略大,主要是因为ETFE材料徐变效应.
|
图6 ETFE气枕3.5 kPa下膜面形态(三维裁切) |
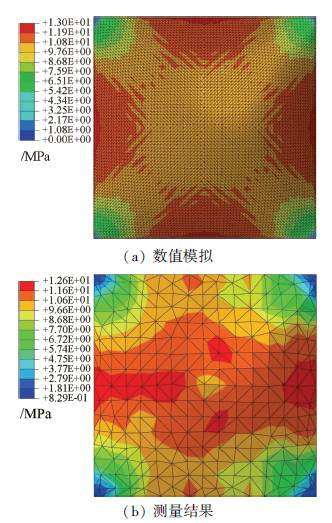
膜面的应力分布影响材料的徐变特性和结构的安全性能,正方形ETFE气枕的膜面应力分布见图 7.试验结果与数值模拟相对比可知,两者的分布规律较为接近,但数值模拟的应力分布更加均匀和对称,试验结果具有局部变化大的特点,两者的最大应力存在0.4 MPa的误差,试验结果略小.
|
图7 ETFE气枕3.5 kPa下膜面应力分布(三维裁切) |
提取气枕三维形面中截面和对角线的外形轮廓,并将试验结果与数值模拟进行对比,见图 8.由中截面外形的对比可知,两者很接近,数值模拟略大于试验结果.由对角线外形的对比可知,两者在角部区域的差异较大,表现为试验结果大于数值模拟;相应地,图 7中所示的应力分布表明,试验结果的角部区域比数值模拟要小一些.

|
图8 ETFE气枕剖面外形轮廓(三维裁切) |
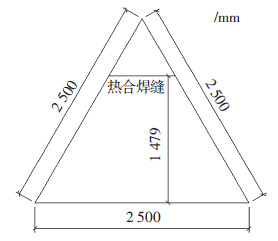
基于平面裁切的成形设计方法,通过简单的平面裁切和焊接来形成气枕结构.见图 9,模型为边长2.5 m的正三角形ETFE气枕,上、下膜面均按平面裁切.受到薄膜卷材宽度的限制,双层膜面均由两片膜片经275度高温热合焊接而成.气枕边缘处也采用热合加工,并包裹直径为6 mm的PE棒,然后利用铝合金夹具通过螺栓张拉固定于钢框架上.下膜面的角部区域分别预留了两个直径为6 mm的圆孔,并安装带有密封性能的气门芯,用来连接压力控制系统.
|
图9 试验模型平面尺寸(平面裁切) |
首先进行准备工作,在气枕上膜面按网格粘贴靶点,架设三角架,安放相机、调焦并进行校准,放置高精度标尺,安装激光位移计,压力控制系统通过预留的两个配有密封性能的气门芯进行接入,试验系统见图 10,试验过程分为3个连续阶段:

|
图10 ETFE气枕试验系统(平面裁切) |
1) 充气加压阶段.利用压力控制系统对ETFE气枕进行充气加压至4 kPa.
2)稳压徐变阶段.当气枕内压充至4 kPa,利用压力控制系统对气枕内压进行恒定控制.为了防止压力控制系统频繁开关,压力保持的工作范围为3.985~4.015 kPa,持续时间为25 min.
3)徐变恢复阶段.徐变试验结束后,将ETFE气枕内压降为0.5 kPa,持续时间为24 h.
试验过程中,在设定的时间点利用三维摄影测量系统和激光位移传感器对上膜面整体外形、下膜面矢高变化分别进行测量,ETFE气枕内部压力由压力控制系统自动记录.
3.3 试验结果与分析基于测量外形,应用引入线性调整理论的力密度法,结合实际测得的气枕内压及边界条件,通过计算可得到不同内压下的膜面应力分布[18, 19].对三角形ETFE气枕模型进行数值模拟,可得到相应的膜面外形、应力分布和变化规律.
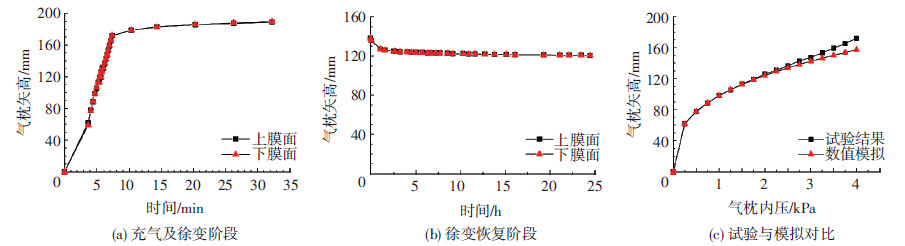
为验证摄影测量结果的有效性和双层膜面变化的相似性,三角形气枕的上、下层膜面的矢高均被测量,并与数值模拟的结果进行对比,见图 11.由试验结果与数值模拟的对比可知,在内压小于2.0 kPa时,两者的矢高变化相近,差值范围为-0.62~0.53 mm;当内压大于2.0 kPa时,两者之间的差值增大,试验结果大于数值模拟,最大差值为14.7 mm,这是由于数值分析过程并没有考虑材料的徐变效应.
|
图11 ETFE气枕矢高变化(平面裁切) |
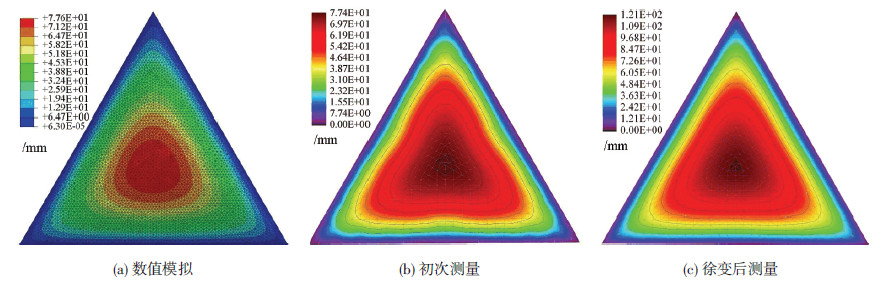
三角形ETFE气枕的膜面外形见图 12.气枕初次成形、内压为0.5 kPa时,实测的气枕矢高较低、约为77.4 mm,矢跨比为1/19;试验结果与数值模拟相比,总体变化一致,但数值模拟的结果略大,且变化层次更加饱满光滑.随着ETFE薄膜产生徐变,气枕矢高增大,膜面整体外形升高,矢高增大为121 mm,矢跨比增大为1/12.
|
图12 ETFE气枕0.5 kPa下膜面外形(平面裁切) |
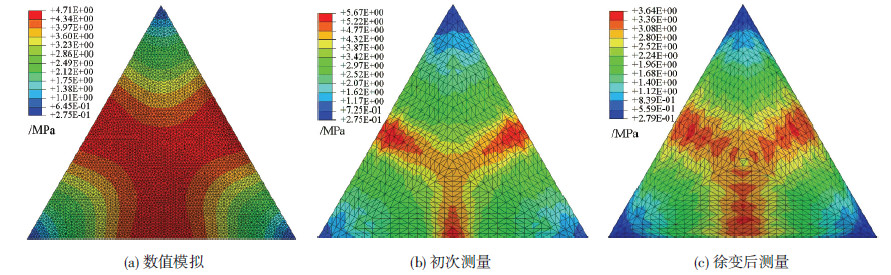
三角形ETFE气枕的膜面应力分布见图 13.气枕初次成形、内压为0.5 kPa时,实测的气枕膜面最大应力为5.67 MPa;试验结果与数值模拟相比,总体规律一致,但数值模拟的极大应力区域比试验结果要大,最大应力为4.71 MPa,小于试验结果.随ETFE薄膜产生徐变,气枕的膜面应力分布减小,最大应力为3.64 MPa.
|
图13 ETFE气枕0.5 kPa下膜面应力分布(平面裁切) |
根据ETFE气枕两种成形方法的设计过程及相应的分析过程状态和力学模型,通过两个ETFE气枕充气成形试验和数值模拟,得到结构的膜面形态和应力分布及其变化规律.通过对比分析,可得到:
1)对于三维裁切成形模型,气枕膜面形态的试验结果与数值模拟最大误差为4 mm,应力分布最大值相差0.4 MPa,吻合度较高.
2)对于平面裁切成形模型,初次成形时的气枕膜面形态与应力分布的试验与数值相一致,约为77.4 mm,最大应力约为5 MPa;随ETFE材料发生徐变,气枕矢高升高为121 mm,应力最大值减小为3.64 MPa,矢跨比由1/19增大为1/12.
因此,试验和分析验证了本文所提出的成形设计方法.根据自身特点,三维裁切方法适用于任意气枕外形,特别是矢高较大的气枕,而平面裁切方法适用于工程量大、对气枕外形无特殊要求的项目.
| [1] | 陈务军. 膜结构工程设计[M]. 北京:中国建筑工业出版社,2005.( 5) 5) |
| [2] | HOUTMANN R. Design recommendations for ETFE foil structures, annex 5 TensiNet european design guide for tensile structures[M]. Brussels: TensiNet, 2013.( 1) 1) |
| [3] | HU J, CHEN W, ZHAO B, et al. Uniaxial tensile mechanical properties and model parameters determination of ethylene tetrafluoroethylene (ETFE) foils[J]. Construction and Building Materials, 2015, 75: 200-207.( 2) 2) |
| [4] | HU J, CHEN W, LUO R, et al. Uniaxial cyclic tensile mechanical properties of ethylene tetrafluoroethylene (ETFE) foils[J]. Construction and Building Materials, 2014, 63: 311-319.( 2) 2) |
| [5] | LI Y, WU M. Uniaxial creep property and viscoelastic-plastic modelling of ethylene tetrafluoroethylene (ETFE) foil[J]. Mechanics of Time-Dependent Materials, 2015, 19(1): 21-34.( 3) 3) |
| [6] | CHARBONNEAU L, POLAK M A, PENLIDIS A. Mechanical properties of ETFE foils: testing and modelling[J]. Construction and Building Materials, 2014, 60: 63-72.( 2) 2) |
| [7] | 傅学怡, 顾磊, 施永芒, 等. 北京奥运国家游泳中心结构初步设计简介[J]. 土木工程学报, 2004, 37(2): 1-11.( 1) 1) |
| [8] | 徐国宏, 袁行飞, 傅学怡, 等. ETFE气枕结构设计--国家游泳中心气枕结构设计简介[J]. 土木工程学报, 2005, 38(4): 66-72.( 1) 1) |
| [9] | 吴明儿, 刘建明, 张其林. ETFE 薄膜气枕模型试验研究[J]. 建筑结构学报, 2009, 29(6): 126-131.( 1) 1) |
| [10] | WU M, WU Y, KIM J Y. ETFE foil spring cushion structure and its analytical method[J]. Thin-Walled Structures, 2011, 49(9): 1184-1190.( 1) 1) |
| [11] | 顾磊, 王鹏, 陈世平, 等. ETFE气枕模型试验与有限元分析[J]. 建筑结构学报, 2012, 33(5): 46-52.( 1) 1) |
| [12] | 李鹏, 杨庆山, 杨一龙. ETFE气枕力学性能试验研究及有限元分析[J]. 建筑结构学报, 2015, 36(3): 147-157.( 1) 1) |
| [13] | 张建, 杨庆山, 李波. 气枕式充气膜结构形态与受力分析[J]. 哈尔滨工业大学学报, 2009, 40(12): 2020-2023.( 1) 1) |
| [14] | 赵兵, 陈务军, 何艳丽. ETFE薄膜双层气枕结构试验研究[J]. 空间结构, 2013, 19(1): 65-72.( 3) 3) |
| [15] | ZHAO J, CHEN W, FU G, et al. Computation method of zero-stress state of pneumatic stressed membrane structure[J]. Science China Technological Sciences, 2012, 55(3): 717-724.( 4) 4) |
| [16] | 何艳丽, 陈务军, 赵俊钊. 充气膜结构的成形理论与试验研究[J]. 工程力学,2013, 30(4): 269-274.( 1) 1) |
| [17] | HU J, CHEN W, ZHAO B, et al. Experimental studies on summer performance and feasibility of a BIPV/T ethylene tetrafluoroethylene (ETFE) cushion structure system[J]. Energy and Buildings, 2014, 69: 394-406.( 1) 1) |
| [18] | ZHAO B, CHEN W, HU J, et al. Mechanical properties of ETFE foils in form-developing of inflated cushion through flat-patterning[J]. Construction and Building Materials, 2016, 111: 580-589. ( 2) 2) |
| [19] | ZHAO B, CHEN W, HU J, et al. An innovative methodology for measurement of stress distribution of inflatable membrane structures[J]. Measurement Science and Technology, 2016, 27(2): 025002.( 2) 2) |
 2016, Vol. 48
2016, Vol. 48


