2. 天津大学 建筑工程学院, 300072 天津;
3. 水利工程仿真与安全国家重点实验室(天津大学), 300072 天津
2. School of Civil Engineering, Tianjin University, 300072 Tianjin, China;
3. State Key Laboratory of Hydraulic Engineering Simulation and Safety (Tianjin University), 300072 Tianjin, China
随着中国经济的快速发展和人们审美水平的不断提高,建筑形式日益多样化,大跨复杂空间结构得到广泛应用.根据中国规范要求,对这类结构不仅要进行弹性分析,而且还要进行动力弹塑性分析以获得其在大震下的抗震性能.
ABAQUS是一套功能强大的通用有限元软件,它不仅具有丰富的单元库和材料库,而且允许用户进行二次开发.但是,与它强大的计算功能相比,其前处理能力并不便捷.相比而言,SAP2000软件因其直观的用户界面和快速的对象捕捉和选择功能,使用户可以快速建立模型.结合ABAQUS和SAP2000软件各自的优势,作者开发了将SAP2000模型转化到ABAQUS中的接口程序TJU.SAP2ABAQUS,提高了建模效率[1].
实际的地震地面运动是一个复杂的时间-空间过程,以往的抗震设计多集中于地震动的时变特性,而较少考虑地震动的空间变化[2].然而,对大跨空间结构而言,地震动的空间变化对其反应有一定的影响,尤其是结构的跨度和规模较大时,这种影响尤其明显[3, 4].李玉刚等[5]对影响单层球壳结构地震空间相关性效应的因素进行了研究;杨庆山等[6]对多点地震激励下国家体育场结构的反应进行了分析;丁阳等[7]对大跨度体育馆结构进行了多点地震非平稳随机反应分析.大跨空间展览馆结构是重要的公共建筑,如何在这种复杂大跨结构的抗震设计中考虑多点地震激励的影响有待进一步的研究.
本文以某大跨复杂空间展览馆结构为工程背景,分别进行了单向一致、单向多点、三向一致和三向多点激励下结构的动力弹塑性分析,比较了地震一致激励和多点激励下结构的反应,本研究可为此类大跨结构的抗震分析和设计提供参考.
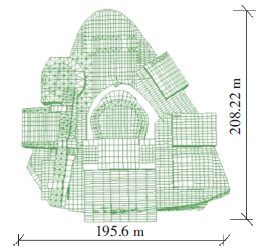
1 工程概况某大跨空间展览馆结构,高度47.85 m,平面形状不规则(关于x轴和y轴均不对称),近似呈椭圆形,短轴(平行于x方向)和长轴(平行于y方向)分别为195.60 m和208.22 m,见图 1.结构所在场地的设防烈度为7度,设计基本加速度为0.1 g,设计地震分组为第一组,场地类别属于Ⅱ类.
|
图1 大跨展览馆结构平面图 |
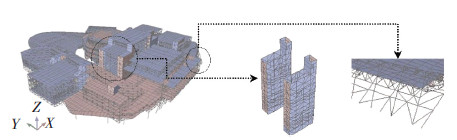
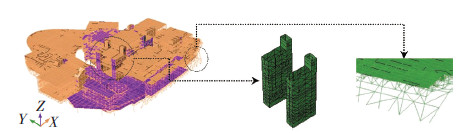
采用SAP2000软件建立结构的有限元模型,见图 2.利用开发的TJU.SAP2ABAQUS接口程序,将SAP2000模型转化,得到用于结构动力弹塑性分析的ABAQUS模型,见图 3.从转换前、后模型的形状可看出,SAP2000模型和ABAQUS模型基本一致.
|
图2 SAP2000有限元模型 |
|
图3 ABAQUS有限元模型 |
采用SAP2000和ABAQUS软件分别对结构进行模态分析,模型前5阶自振频率对比见表 1.转换前、后模型的自振频率比较接近(最小仅相差0.4%).
| 表1 SAP2000和ABAQUS模型自振频率比较 |
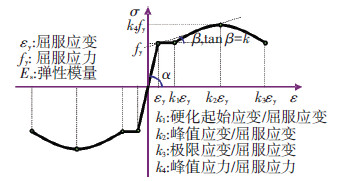
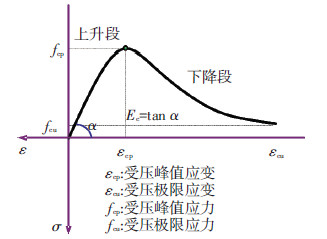
图 4、5分别给出了钢材和混凝土本构的骨架曲线,相应的滞回曲线、加卸载规则改进及相关ABAQUS子程序开发见文献[8].
|
图4 钢材本构骨架曲线 |
|
图5 混凝土本构骨架曲线 |
利用ABAQUS进行大跨展览馆结构的动力弹塑性分析时,采用Rayleigh阻尼体系,结构振型阻尼比ζ取0.02[9].Rayleigh阻尼中的质量系数α和刚度系数β为[10]
| $\alpha = \zeta \frac{{2{\omega _i}{\omega _j}}}{{{\omega _i} + {\omega _j}}},\;\;\;\beta = \zeta \frac{2}{{{\omega _i} + {\omega _j}}}.$ | (1) |
式中ωi和ωj分别是结构第i、j阶圆频率.
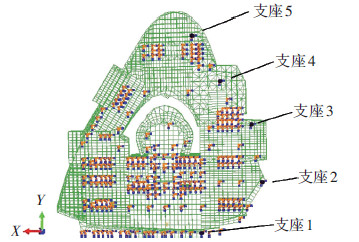
3 多点地震激励 3.1 多点地震动输入以跨度较大的长轴(y向)作为地震动的主输入方向,多点地震动输入时,将底部所有支座在y方向上平均划分为5个区域,每个区域找出一个代表支座作为多点地震动的输入位置,见图 6.
|
图6 结构底部支座分布 |
采用可考虑低频分量的Clough-Penzien修正白噪声目标功率谱模型[11],其表达式为
| $\begin{array}{l} S\left( \omega \right) = {S_0}\frac{{\omega _{\rm{g}}^4 + 4\zeta _{\rm{g}}^2\omega _{\rm{g}}^2{\omega ^2}}}{{{{\left( {\omega _{\rm{g}}^2 - {\omega ^2}} \right)}^2} + 4\zeta _{\rm{g}}^2\omega _{\rm{g}}^2{\omega ^2}}} \times \\ \;\;\;\;\;\;\;\;\;\;\frac{{{\omega ^4}}}{{{{\left( {\omega _{\rm{f}}^2 - {\omega ^2}} \right)}^2} + 4\zeta _{\rm{f}}^2\omega _{\rm{f}}^2{\omega ^2}}}. \end{array}$ | (2) |
式中:ω为圆频率,S0为谱强度因子,ωg和ζg分别为场地的卓越圆频率和阻尼比,ωf和ζf分别为与地震动低频分量相关的参数.按照7度设防考虑,所在场地为Ⅱ类,式(2)中各参数的取值分别为:S0=0.042,ζg=0.075,ωg=21.40,ωf=0.38,ζf=0.49[12].
根据支座的位置关系和选定的地震动参数,采用开发的多点地震动模拟程序生成对应于支座位置的地震动加速度时程.
4 一致与多点激励下地震反应分析对该大跨空间展览馆结构分别进行单向多点和三向多点激励下的地震反应分析,并与一致激励下的反应进行对比.单向地震输入沿结构长轴方向(y向),三向地震动输入时,长轴、短轴和竖向地震动峰值比例为1:0.85:0.65,分别对应于结构的y向、x向和z向.按7度设防烈度考虑,根据《建筑抗震设计规范》[9] 规定,对应罕遇的峰值地震加速度(PGA)为0.22 g.
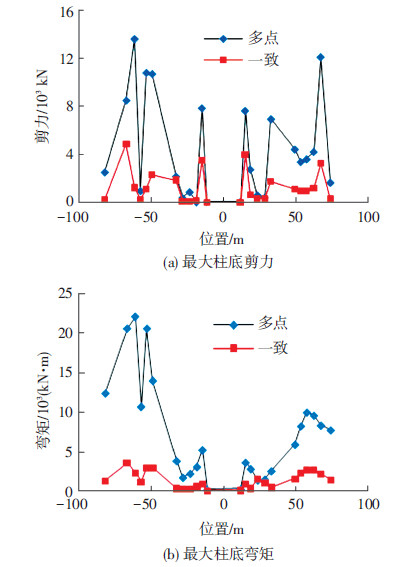
4.1 一致与多点激励(单向)的结构反应 4.1.1 最大柱底剪力和弯矩图 7给出了单向多点和一致激励时,结构底层x-y平面内(y=79.1m处)24根柱子底部剪力和弯矩的最大值.可看出,受到地震动空间变化的影响,柱底剪力和弯矩均有所增加,尤其是1/4跨和1/8跨附近,柱子内力增大最为明显,其原因为:地震动的空间变化对柱子底部激励的不一致性使得对结构两侧柱子内力的影响更大.
|
图7 单向地震激励下最大柱底内力 |
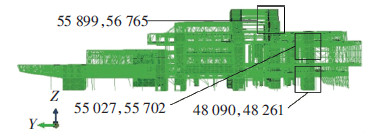
表 2给出了罕遇地震下,单向多点和一致激励时,剪力墙的最大应力,选取的剪力墙单元编号见图 8.从表 2可看出,与一致地震激励相比,考虑多点激励时,底部和中部剪力墙的最大应力有所增加,上部剪力墙的最大应力减小.
| 表2 单向地震激励下剪力墙最大应力 |
|
图8 选取的剪力墙位置 |
表 3给出了罕遇地震下、单向多点和一致激励时,结构顶部节点y向的最大位移.与一致激励相比,单向多点激励下结构顶部节点的最大位移增加了38.4%.因此,进行抗震分析时,不能忽略地震动的空间变化对大跨结构位移的影响.
| 表3 单向地震激励下顶部节点最大位移 |
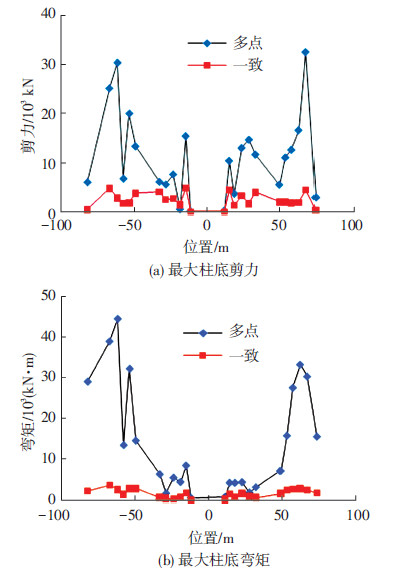
考虑三向地震动输入,同样选取结构底部x-y平面内(y=79.1 m处)24根柱子进行分析.图 9给出了三向多点和一致激励时,最大柱底剪力和弯矩.与一致激励相比,多点激励下结构最大柱底剪力和弯矩变化较大,尤其是1/4跨以外柱底部内力变化最为显著,相比较而言,结构中部最大柱底内力较一致激励变化不大,地震动的空间变化对大跨展览馆结构不同位置的柱底内力影响不同.
|
图9 三向地震激励下最大柱底内力 |
表 4给出了罕遇地震下,三向一致和三向多点激励时,剪力墙的最大应力 (选取的剪力墙单元与4.1.2节相同)与三向一致激励相比,考虑三向多点激励时,剪力墙的应力同样有增有减,底部和中部剪力墙的应力有较为明显的增大;上部剪力墙的最大应力有增有减,说明三向多点激励对结构上部剪力墙内力的影响较单向多点激励时有所增大.
| 表4 三向地震激励下剪力墙最大应力 |
表 5给出了罕遇地震下、三向一致和多点激励时,大跨空间展览馆结构顶部节点的最大位移.三向多点激励下,结构顶部的最大位移较三向一致激励时增加了34.8%.由此说明,对此类大跨结构进行抗震设计时,有必要考虑地震动的空间变化对剪力墙内力和位移的影响.
| 表5 三向地震激励下顶部节点最大位移 |
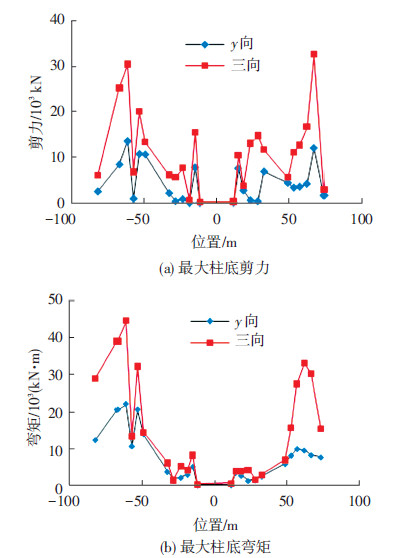
图 10给出了7度罕遇地震下,单向(y向)多点和三向多点激励时,大跨展览馆结构的最大柱底剪力和弯矩.与单向多点地震激励相比,三向多点激励下最大柱底剪力和弯矩均有所增加,最大柱底剪力增加了近250%.而且,大跨结构底部不同位置的柱子内力,受地震动空间变化的影响程度也不相同.三向多点激励时,结构1/8跨附近柱底剪力和弯矩较单向多点激励下增大最为明显,说明此类大跨结构进行抗震计算时,不能仅考虑地震动一个分量的空间变化,须同时考虑地震动3个方向的空间变化对结构柱子剪力和弯矩的影响.
|
图10 多点激励下最大柱底内力 |
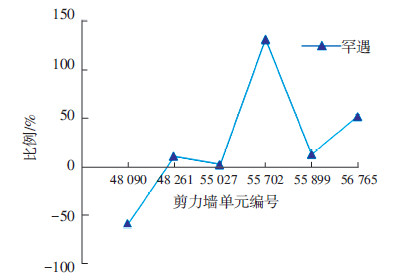
图 11给出了罕遇地震下,单向和三向多点激励时,剪力墙最大应力的变化情况(选取的剪力墙单元与4.1.2 节相同).图中,比例=(三向多点应力-单向多点应力)/单向多点应力.
|
图11 剪力墙最大应力变化 |
从图中可看出,与单向多点激励相比,三向多点激励下底部剪力墙的最大应力有增有减,而中部和上部剪力墙的最大应力均有所增加.罕遇地震下,单向多点和三向多点激励时,结构顶部节点的最大位移分别为2.482 m和3.162 m.与单向多点激励相比,三向多点激励下顶部节点的最大位移增加了27.4%.由此说明,有必要考虑地震动3个方向的空间变化对剪力墙内力和结构位移的影响.
5 结 论1) 多点激励下结构的最大柱底剪力和弯矩、顶部的最大位移以及剪力墙的最大应力明显大于一致激励下的情况,计算结果表明对于此类大跨空间结构考虑多点激励的动力弹塑性分析十分必要.
2) 与单向多点激励相比,在三向多点激励下,结构的最大柱底剪力、弯矩和剪力墙的最大应力有增有减,结构顶部最大位移也有显著增大,说明有必要考虑地震动3个方向的空间变化对此类大跨结构内力和位移的影响.
3)与一致激励相比,多点地震激励对结构中部柱子内力的影响较小,对结构两侧柱子内力的影响较大,说明进行抗震弹塑性分析时,地震动的空间变化对此类大跨空间结构柱子内力的影响不容忽视.
| [1] | 柳国环, 练继建, 国巍.结构动力弹塑性与倒塌分析(Ⅱ):SAP2ABAQUS接口技术、开发与验证[J]. 地震研究, 2014, 37(1):132-140.( 1) 1) |
| [2] | 李宏男.结构多维抗震理论[M]. 北京:科学出版社, 2006.( 1) 1) |
| [3] | 刘先明, 叶继红, 李爱群.多点输入反应谱法的理论研究[J]. 土木工程学报, 2005, 38(3):17-22.( 1) 1) |
| [4] | 柳国环, 李宏男, 田利.九江长江大桥在多点多维地震激励下的反应分析[J]. 振动与冲击, 2009, 28(9):204-209.( 1) 1) |
| [5] | 李玉刚, 支旭东, 范峰.单层球壳结构地震空间相关性效应的影响因素研究[J]. 空间结构, 2013, 19(3):9-13.( 1) 1) |
| [6] | 杨庆山, 刘文华, 田玉基.国家体育场在多点激励作用下的地震反应分析[J]. 土木工程学报, 2008, 41(2):35-41.( 1) 1) |
| [7] | 丁阳, 林伟, 李忠献.大跨度空间结构多维多点非平稳随机地震反应分析[J]. 工程力学, 2007, 24(3):97-103.( 1) 1) |
| [8] | 柳国环, 练继建, 国巍.结构动力弹塑性与倒塌分析(Ⅰ):滞回曲线改进、ABAQUS子程序开发与验证[J]. 地震研究, 2014, 37(1):123-131.( 1) 1) |
| [9] | 中华人民共和国住房和城乡建设部.建筑抗震设计规范:GB 50011-2010[S]. 北京:中国建筑工业出版社, 2010.( 2) 2) |
| [10] | CHOPRA A K.结构动力学-理论及其在地震工程中的应用[M]. 2版.谢礼立, 吕大刚, 等译.北京:高等教育出版社, 2007.( 1) 1) |
| [11] | CLOUGH R W, PENZIEN J.Dynamics of structures[M]. 3rd ed.New York:McGraw-Hill, 1993.( 1) 1) |
| [12] | 潘晓东.非平稳随机地震下堤坝非线性有效应力动力响应可靠度分析[D]. 杭州:浙江大学, 2004.( 1) 1) |
 2016, Vol. 48
2016, Vol. 48


