冷轧带肋钢筋是上世纪60年代首先在德国、荷兰和比利时研制成功,而后得到广泛应用的一种高效建筑钢材[1].中国于上世纪80年代后期开始引进冷轧带肋钢筋生产设备,目前在预制构件中已逐步取代冷拔低碳钢丝,并在现浇结构中也有较多应用,当应用于现浇楼盖中时,可节约35%~40%的钢材[2, 3].与普通冷加工钢筋相比,冷轧带肋钢筋具有良好的延伸率,机械加工性能和可焊性[4].冷轧带肋钢筋可焊接为钢筋网,与传统的现场人工绑扎钢筋相比,采用钢筋焊接网施工机械化程度高,具有高效、准确和流水线作业的特点,可有效降低成本和加快工程进度.由于横向钢筋与纵向钢筋成为整体,钢筋焊接网与混凝土的锚固性能好[5, 6],整体应力传递更为均匀[7, 8].在国外,冷加工钢筋焊接网被广泛应用于楼板、剪力墙、桥梁和高速公路中[9].在国内,将冷轧带肋钢筋焊接网应用于剪力墙中已有较多研究[10, 11],而板类构件受弯和滞回性能的研究尚少,目前作为非抗震构件使用.
本研究对配置CRB600H和CRB550两类冷轧带肋钢筋焊接网板的受弯性能进行探讨.通过钢筋材性拉伸试验,获得了CRB600H钢筋、CRB550钢筋的应力-应变关系,进而得到了CRB600H、CRB550钢筋的屈服强度、极限强度、弹性模量、最大力伸长率等力学性能指标;完成了32块CRB600H、CRB550钢筋焊接网混凝土板的抗弯性能试验,提出了适用于CRB600H及CRB550冷轧带肋钢筋焊接网混凝土板的正截面承载力、短期刚度及裂缝宽度计算公式.
1 钢筋力学性能 1.1 试验设备和试件采用WDW-100型万能试验机进行钢筋拉伸性能试验,试验机额定荷载100 kN,力测量精度优于0.1 kN,引伸计精度优于1×10-3 mm.
分别对CRB600H和CRB550两种钢筋进行试验.钢筋直径有8、10、12 mm三种,各直径钢筋分为无焊点(一字型)和有焊点(十字形)两类.
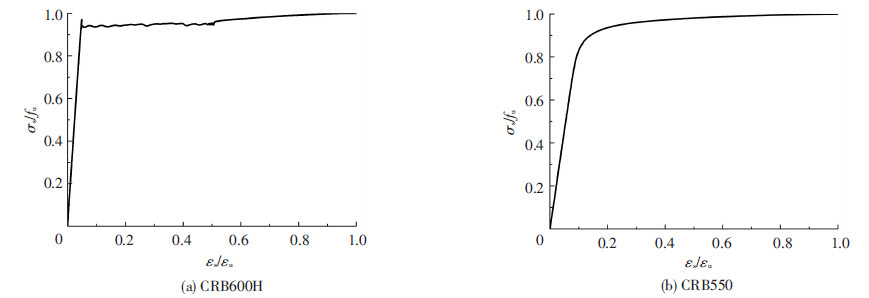
1.2 试验结果按文献[12]规定的方法进行钢筋拉伸试验.CRB600H与CRB550钢筋的典型应力-应变关系见图 1.初始加载阶段,CRB600H钢筋为弹性,达到屈服应力时,钢筋的应力-应变曲线出现上下波动,之后钢筋的应变持续增长而应力基本保持不变,有明显的屈服平台.超过屈服阶段后,钢筋进入强化阶段,其应力随应变增大而提高.达到极限应力后,钢筋局部出现颈缩,直至断裂.CRB600H钢筋的应力-应变曲线形状与热轧钢筋相似.与CRB600H钢筋相比,CRB550钢筋无明显屈服点,其最大力伸长率和断后总伸长率均小于CRB600H钢筋.达到极限应力后,钢筋局部出现颈缩,随后断裂.CRB600H钢筋的断裂处颈缩明显,断口呈“V”型或斜面型.CRB550钢筋断口特征与CRB600H钢筋相同,但断面收缩率较小.
|
图1 钢筋典型应力-应变曲线 |
试验结果表明,无焊点和有焊点钢筋的拉伸应力-应变曲线相同,焊点对钢筋的拉伸应力-应变曲线无影响,钢筋的断裂截面均在非焊点处,表明采用电阻点焊的焊接接头对钢筋抗拉强度无削弱.钢筋的力学性能指标见表 1.
| 表1 冷轧钢筋力学性能 |
共设计32块冷轧带肋钢筋焊接网混凝土板,试验板长度均为3 300 mm,宽度为700 mm,纵筋保护层厚度为20 mm,其配筋情况和相关参数列于表 2.其中B1-1~B2-8配置CRB600H钢筋;B3-1~B4-8配置CRB550钢筋.
| 表2 试验板参数 |
为便于观测板底裂缝,采用倒置的简支加载方式.在试验板纯弯段内的纵筋上布置钢筋应变片,在试验板受压区布置混凝土应变片,分别用以测量钢筋和混凝土应变.在试验板加载点、跨中和支座处安装位移计传感器共10个,位移测点沿板宽方向距板边缘100 mm.加载装置见图 2.

|
图2 试验装置布置(mm) |
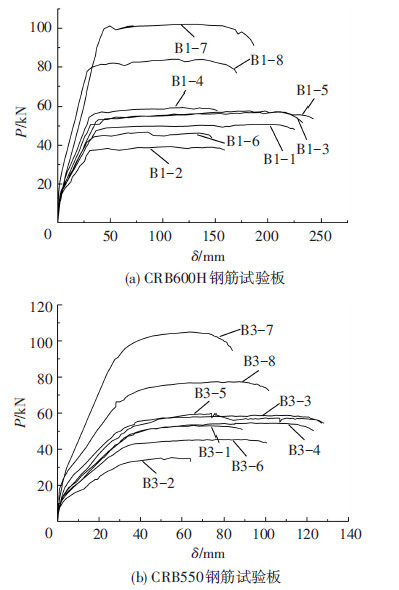
试验板开裂之前跨中位移与荷载之间呈线性关系.加载至15%~30%Pu时,试验板受拉区混凝土出现第一条(或第一批)裂缝,裂缝首次出现的位置一般在靠近支座的纯弯段内.首批裂缝出现之后,试验板的跨中位移随荷载增长较之前加快,荷载-位移曲线发生第一次偏折.当荷载达到40%~60%Pu时,纯弯段内的裂缝出齐且多数贯通,剪弯段内仍有新裂缝出现,缝宽度随荷载提高不断增长.当荷载达到70%~85%Pu时,纯弯段裂缝全部贯通,剪弯段裂缝基本出齐.加载至90%~95%Pu时,试验板内纵筋发生屈服,钢筋应变急剧增大,裂缝宽度和跨中位移迅速发展,试件的荷载-位移曲线发生第二次偏折.在继续加载至Pu的过程中,试验板受拉区混凝土产生剥落和掉渣现象,达到Pu后,配置CRB600H钢筋的试验板多因混凝土被压碎而破坏;配置CRB550钢筋的试验板多因钢筋被拉断而破坏.试验结果见表 3,荷载挠度曲线见图 3、4.
| 表3 试验结果 |
|
图3 C20混凝土试验板荷载-挠度曲线 |
受弯构件截面抵抗矩塑性影响系数主要与纵向受拉钢筋配筋率、截面高度、混凝土强度等因素有关[13],文献[14]采用以下公式计算截面抵抗矩塑性影响系数:
| $\gamma = \left( {0.7 + \frac{{120}}{h}} \right){\gamma _{\rm{m}}}.$ | (1) |
式中:h < 400 mm时,取h=400 mm;对矩形截面取γm=1.55,可计算出γ=1.55.
开裂弯矩计算公式为
| ${M_{{\rm{cr}}}} = \gamma {f_{\rm{t}}}{W_0},$ | (2) |
式中W0是将混凝土板中钢筋面积折算为混凝土后的换算截面的截面抵抗矩.
将式(1)带入式(2)可得各试验板开裂弯矩的计算值Mcrc.将开裂弯矩的计算值与实测开裂弯矩(Mcrt)进行比较,得出试验板开裂弯矩计算值与实测值比值Mcrc/Mcrt的平均值1.063,变异系数δ=0.117.开裂弯矩的计算值与实测值吻合良好,表明横向钢筋未为试验板的开裂弯矩产生影响,冷轧带肋钢筋焊接网混凝土板的开裂弯矩可按现行规范[14]计算.
3.2 正截面受弯承载力分析根据文献[15],焊接钢筋网混凝土受弯构件的受弯承载力可按式(3)计算:
| $\left\{ \begin{array}{l} {\alpha _1}{f_{\rm{e}}}bx = {f_{\rm{y}}}{A_{\rm{s}}},\\ {M_{\rm{u}}} = {\alpha _1}{f_{\rm{e}}}bx\left( {{h_0} - \frac{x}{2}} \right). \end{array} \right.$ | (3) |
式中:Mu为试件的受弯承载力;fc为混凝土轴心抗压强度;α1 为受压区混凝土矩形应力图的应力值与fc之比,当混凝土强度等级不超过C50时,取1.0;b为板宽;x为混凝土等效受压区高度;h0 为截面有效高度;fy为钢筋屈服强度(CRB550钢筋取其抗拉强度).
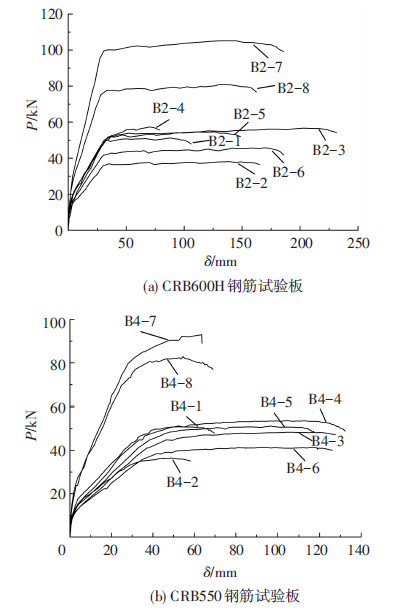
由试验板的荷载-挠度曲线(图 3、4)可知,配置CRB600H钢筋的试验板在钢筋屈服后荷载随挠度增长基本不再提高;而配置CRB550钢筋的试验板在钢筋屈服后荷载随挠度增长仍有少量提高.结合试件的破坏模式,分别假定当试件达到正截面承载力极限状态时,CRB600H钢筋达到其屈服强度,而CRB550钢筋达到其抗拉强度.基于上述假定,将由式(3)获得的这类板正截面承载力计算值Muc与实测值Mut进行比较,Muc/Mut的平均值为0.94,变异系数δ=0.08,计算值与试验结果吻合良好,且偏于安全,表明计算模型基本符合事实.对比结果见表 4.
|
图4 C30混凝土试验板荷载-挠度曲线 |
| 表4 正截面承载力计算值与实测值对比 |
上述分析结果表明,配置CRB600H钢筋焊接网的混凝土板正截面承载力可按现行规范[15]计算.为偏于安全,对于配置CRB550钢筋焊接网的混凝土板正截面承载力,在设计计算中应取钢筋的名义屈服强度.
3.3 短期抗弯刚度分析由抗弯刚度的定义和理论分析可知,试验板的短期抗弯刚度可根据文献[14]计算为
| ${B_{\rm{s}}} = \frac{M}{\varphi } = \frac{{{E_{\rm{s}}}{A_{\rm{s}}}h_0^2}}{{\frac{\psi }{\eta } + \frac{{{\alpha _{\rm{E}}}\rho }}{\zeta }}},$ | (4) |
式中:As为受拉钢筋截面面积,h0为截面有效高度,ψ为裂缝间纵向受拉钢筋应变不均匀系数,αE为钢筋弹性模量与混凝土弹性模量的比值,式中ρ为受拉钢筋配筋率,η为内力臂系数.
当已知混凝土弹性模量、受拉纵筋的面积、试验板尺寸等条件时,确定ζ、η和ψ3个参数取值,即可计算受弯构件的短期刚度.
3.3.1 受压区边缘混凝土平均应变综合系数ζ由文献[14]可知,受压区边缘混凝土平均应变综合系数的表达式为
| $\zeta = \frac{M}{{{\varepsilon _{{\rm{cm}}}}{E_{\rm{c}}}bh_0^2}}.$ | (5) |
根据试验时的跨中弯矩M(取Mcr≤M≤My)和对应的受压边缘实测混凝土平均应变εcm,以及混凝土实测弹性模量和试验板的尺寸,按式(5)可计算得到ζ值.获得ζ值后,对各试验板不同跨中弯矩下的$\frac{{{\alpha _{\rm{E}}}\rho }}{\zeta }$和0.2+6αEρ进行计算可知,$\frac{{{\alpha _{\rm{E}}}\rho }}{\zeta }$/(0.2+6αEρ)的平均值为1.026,变异系数δ=0.228,二者吻合良好.故对于这类混凝土矩形板,ζ可按文献[14]中的公式计算:
| $\zeta = \frac{{{\alpha _{\rm{E}}}\rho }}{{0.2 + 6{\alpha _{\rm{E}}}\rho }}.$ | (6) |
由试验板受压区边缘混凝土压应变和受拉钢筋拉应变的实测值,根据平截面假定可算出截面的受压区高度x,则有$\eta \approx \frac{{\left( {{h_0} - x} \right) + {x_{\rm{c}}}}}{{{h_0}}}$,其中xc为混凝土受压区应力分布图形的合力点到中和轴的距离,可根据积分得到.
在短期荷载作用下,当Mcr≤M≤My时,开裂截面的内力臂基本不变.由文献[16]可知,普通混凝土受弯构件内力臂系数的计算公式为
| $\eta = 1 - 0.4\sqrt {{\alpha _{\rm{E}}}\rho } .$ | (7) |
混凝土受弯构件的η一般为0.83~0.93[17].由式(7)可得本研究中试验板的内力臂系数为0.859~0.962(平均值为0.918),符合一般规律.内力臂系数计算值与实测值比值(ηc/ηt)的平均值为1.01,变异系数δ=0.025.试验值与计算值吻合良好,内力臂系数可按式(7)计算.
3.3.3 钢筋应变不均匀系数ψ钢筋应力不均匀系数为钢筋的平均应变与最大应变的比值($\psi = {{\bar \varepsilon }_{\rm{s}}}/{\varepsilon _{\rm{s}}}$).由文献[15]可知,普通钢筋混凝土受弯构件中受拉钢筋应变不均匀系数计算公式为
| $\psi = \alpha - \frac{{0.65{f_{\rm{t}}}}}{{{\rho _{{\rm{te}}}}{\sigma _{\rm{s}}}}},$ | (8) |
式中:α为系数,对板类构件取α=1.05;ft为混凝土抗拉强度值;ρte为按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率;σs为裂缝截面处受拉钢筋应力.
受拉钢筋应变不均匀系数计算值与实测值比值ψsc/ψst的平均值为1.04,变异系数δ=0.01,计算值与实测值吻合良好.这类板的钢筋应变不均匀系数可按式(8)进行计算.
将按照式(6)~(8)计算得到的ζ、η和ψ代入式(4)可得到试验板的短期刚度.与试验板的实测值进行对比,当Mcr≤M≤My时,可得冷轧带肋钢筋焊接网混凝土板短期刚度计算公式为
| ${B_{\rm{s}}} = \frac{{1.1{E_{\rm{s}}}{A_{\rm{s}}}h_0^2}}{{\frac{\psi }{\eta } + 0.2 + 6{\alpha _{\rm{E}}}\rho }}.$ | (9) |
获得试件的短期刚度后,根据材料力学知识可得试验板在不同弯矩作用下的计算挠度,当Mcr≤M≤My时,挠度计算值(fc)与实测值(ft)之比的平均值为x-=1.03,变异系数δ=0.159,二者吻合良好,故这类板的短期刚度可按式(9)计算.与普通混凝土板相比,冷轧带肋钢筋焊接网混凝土板的短期刚度高约10%.
3.4 裂缝分析 3.4.1 平均裂缝间距由文献[14]可知,混凝土板的平均裂缝间距计算公式为
| ${l_{\rm{m}}}{\rm{ = 1}}{\rm{.9}}c0.08{d_{{\rm{eq}}}}/{\rho _{{\rm{te}}}},$ | (10) |
式中:c为混凝土保护层厚度,deq为受拉区纵向钢筋等效直径.
按式(10)计算得到的裂缝平均间距计算值lmc与实测值比值lmc/lmt的平均值为0.99,变异系数δ=0.158,计算值与试验值吻合良好.表明横向钢筋未对这类板的平均裂缝间距产生影响,冷轧带肋钢筋焊接网混凝土板的平均裂缝间距可按现行规范计算.
3.4.2 平均裂缝宽度由文献[14]可知,受弯构件板侧钢筋重心高度处平均裂缝宽度为
| ${w_{\rm{m}}} = {\alpha _{{\rm{cr}}}}\psi \frac{{{\sigma _{\rm{s}}}}}{{{E_{\rm{s}}}}}{l_{\rm{m}}},$ | (11) |
式中αcr为构件受力特征系数.
由试验数据进行回归可得αcr=0.73,即这类板的平均裂缝宽度为
| ${w_{\rm{m}}} = 0.73\psi \frac{{{\sigma _{\rm{s}}}}}{{{E_{\rm{s}}}}}\left( {1.9c + 0.08\frac{{{d_{{\rm{eq}}}}}}{{{\rho _{{\rm{te}}}}}}} \right).$ | (12) |
将按式(12)得到的平均裂缝宽度wmc与在各级弯矩作用下的实测平均裂缝宽度wmt进行比较,wmc/wmt的平均值为1.05,变异系数δ=0.166.可见平均裂缝宽度计算值与实测值吻合良好,冷轧带肋钢筋焊接网混凝土板在短期荷载作用下的平均裂缝宽度可按式(12)计算.
3.4.3 最大裂缝宽度参照文献[14],冷轧带肋钢筋混焊接网混凝土板的短期最大裂缝宽度ws,max可由平均裂缝宽度wm乘以反映裂缝宽度不均匀性的放大系数τs得到:
| ${w_{{\rm{s}},\max }} = {\tau _{\rm{s}}}{w_{\rm{m}}}.$ | (13) |
对32块试验板6 184个数据点进行统计后得出,各级荷载作用下,试验板的各条裂缝宽度τi与平均裂缝宽度τm的比值近似服从标准差σ=0.37的正态分布.故当裂缝宽度保证率为95%时,τs=1.62.由于未进行长期持荷试验,考虑荷载长期作用影响的扩大系数可暂取为τl=1.5[14].
根据上述分析,配置CRB600H与CRB550钢筋的焊接网混凝土板考虑荷载长期作用影响的最大裂缝宽度计算公式为
| ${w_{\max }} = 1.77\psi {\sigma _{\rm{s}}}/{E_{\rm{s}}}\left( {.9c + 0.08{d_{{\rm{eq}}}}/{\rho _{{\rm{te}}}}} \right).$ | (14) |
1)CRB600H钢筋有明显屈服点,其应力-应变曲线形状与热轧钢筋相似,而CRB550钢筋无明显屈服点.未发现电阻焊点对这两种钢筋的力学性能产生影响.
2)横向钢筋对试验板的开裂弯矩、裂缝间距和裂缝宽度无明显影响,这类板的上述指标仍可按现行规范计算,计算结果与试验结果吻合良好.
3)基于试验结果,获得了这类板受压区边缘混凝土平均应变综合系数、内力臂系数和钢筋应变不均匀系数的计算方法,提出了这类板开裂后到钢筋屈服前的短期刚度计算公式.
4)配置CRB600H钢筋网的试验板多因混凝土被压碎而破坏;配置CRB550钢筋网的试验板多为纵向钢筋被拉断而破坏.基于试验结果提出了考虑这类破坏模式的正截面承载力计算方法.
| [1] | 邢邦圣.冷轧带肋钢筋机械性能的智能预测方法与工艺参数优化研究[D]. 北京:中国矿业大学, 2013.( 1) 1) |
| [2] | 董河毅.冷轧带肋钢筋的发展及在工程中的应用[J]. 山西建筑, 2010, 33:164-165.( 1) 1) |
| [3] | 于秋波, 谢丽丽, 刘立新, 等.CRB600H钢筋在板类构件中的应用[J]. 建筑结构, 2013, 43(增刊1):708-711.( 1) 1) |
| [4] | 谢克非, 李红军, 周天瑞.浅谈冷轧带肋钢筋现阶段的生产应用和发展前景[J]. 南方金属, 2003(3):5-8.( 1) 1) |
| [5] | GRIEZIC A, COOK W D, MITCHELL D.Tests to determine performance of deformed welded wire fabric stirrups[J]. ACI Structural Journal, 1994, 91(2):211-20.( 1) 1) |
| [6] | LEE S L, MANSUR M A, TAN K H, et al.Crack behavior of one-way slabs reinforced with welded wire fabric[J]. ACI Structural Journal, 1989, 86(2):208-216.( 1) 1) |
| [7] | SYAL I C, SYAL R.New trends in concrete construction with welded wire fabric as reinforcement[J]. Indian Concrete Journal, 1997, 71(7):367-372.( 1) 1) |
| [8] | MANSURMA, TAN K H, LEE S L, et al.Crack width in concrete members reinforced with welded wire fabric[J]. ACI Structural Journal, 1991, 88(2):147-154.( 1) 1) |
| [9] | SOLTANI M, AN X H, MAEKAWA K.Cracking response and local stress characteristics of RC membrane elements reinforced with welded wire mesh[J]. Cement and Concrete Composites, 2004, 26(4):389-404.( 1) 1) |
| [10] | 李耕勤, 钱佳茹, 顾万黎.采用冷轧带肋钢筋焊接网的抗震墙性能研究[J]. 建筑结构, 2002, 32(10):29-33.( 1) 1) |
| [11] | 袁宇.高延性冷轧带肋钢筋焊接网片剪力墙抗震性能试验研究[D]. 重庆:重庆大学, 2012.( 1) 1) |
| [12] | 金属材料拉伸试验:GB/T 228.1-2010[S]. 北京:中国标准出版社, 2010.( 1) 1) |
| [13] | 过镇海.混凝土的强度和本构关系[M]. 北京:中国建筑工业出版社, 2004.( 1) 1) |
| [14] | 混凝土结构设计规范:GB 50010-2010[S]. 北京:中国建筑工业出版社, 2010.( 9) 9) |
| [15] | 钢筋焊接网混凝土结构技术规程:JGJ 114-2003[S]. 北京:中国建筑工业出版社, 2014.( 3) 3) |
| [16] | 丁大钧.钢筋混凝土构件抗裂度裂缝和刚度[M]. 南京:南京工学院出版社, 1986.( 1) 1) |
| [17] | 叶列平.混凝土结构[M]. 北京:清华大学出版社, 2005.( 1) 1) |
 2016, Vol. 48
2016, Vol. 48


