2. 中国建筑西南设计研究院有限公司, 610041 成都
2. China Southwest Architectural Design and Research Institute Co., Ltd.,610041 Chengdu, China
天然气在能源结构中的比重越来越大,以及能源储备的需要,国内外都在兴建大型全容式液化天然气(liquefied natural gas,简称LNG)储罐,其由预应力混凝土外罐及钢制内罐组成.在混凝土外罐建造过程中,由于水泥水化放热以及混凝土的收缩特性,混凝土罐体开裂现象很普遍.目前国内外学者展开了大量试验与仿真研究,获得了相关大体积混凝土结构各种热力学指标,并对导致混凝土开裂的因素、规律及数值算法都有探讨[1, 2, 3, 4, 5].文献[6, 7]以国内某LNG储罐为例,介绍了混凝土外罐早期温度裂缝的有限元分析过程,但未考虑混凝土的收缩和徐变效应,且外界气温也只考虑为恒温.
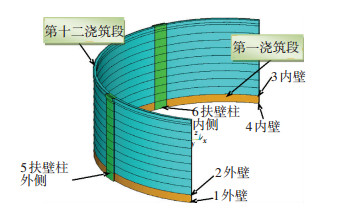
文献[8]利用有限元方法,针对一实际LNG储罐混凝土外罐的施工建造全过程,就混凝土外罐在施工期间的温度场及应力场进行模拟,并对温度裂缝出现的位置及时间进行了预测(见图 1、2);分析中所用模板为DOKA模板,其面板是18 mm厚的胶合木[9].
|
图1 应力结果提取位置 |
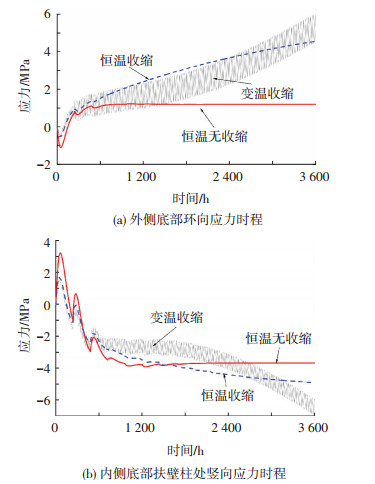
文献[8]的研究结果表明,施工期在5—9月,模拟时间为3 600 h条件下,在第一浇筑段扶壁柱外侧顶部、内侧底部、墙体外侧顶部和底部,墙体内侧顶部和底部的应力结果较大(所在位置分别为图 1中标号5、6、2、1、3、4处).图 2的应力时程对比显示,混凝土收缩对温度应力的影响很大,导致混凝土拉应力的持续增长;拆模后由于外界气温的变化,储罐外壁有幅值为1 MPa的波动.本文将在上述研究基础上,探讨施工中所用的模板材料、施工质量、施工季节及入模温度等因素对裂缝产生的影响规律,并根据分析结果,总结出抗裂措施建议,为同类工程实际施工提供参考.
|
图2 应力时程 |
LNG混凝土外罐施工期间,其早期混凝土的状态参数是随时间变化的,某一时刻t的温度应力不仅与t时刻的温度有关,还与0~t各个时刻的温度、混凝土的凝结状态等有关,因此t时刻的温度应力应为0~t时刻应力累加的结果[10].为此,本文利用ANSYS有限元分析平台,采用增量法并考虑混凝土的松弛系数来求解大体积混凝土早期温度应力,即将节点温升值作为荷载,计算出LNG储罐结构位移与应力的增量.在后处理模块中,将应力增量乘以松弛系数,并将0~t时刻的各增量叠加起来,即得到t时刻温度应力结果.其中时间增量取1 h.
混凝土线膨胀系数取1×10-5/℃,泊松比取0.18,密度取2 400 kg/m3[11].混凝土的弹性模量采用复合指数式 [12]:
| $ E\left( t \right) = {E_{c0}}\left( {1 - {e^{ - a{t^b}}}} \right), $ | (1) |
式中:t为龄期;a,b为常数,a=0.40,b =0.34;Ec0为t→ $ \infty $时混凝土的弹性模量.
考虑到非预应力钢筋率影响,混凝土的弹性模量E′(t) 为
| $ E{'_{\left( t \right)}} = \rho {E_s} + \left( {1 - \rho } \right){E_{\left( t \right)}}, $ | (2) |
式中:ρ为非预应力钢筋配筋率,Es为非预应力钢筋弹性模量.
采用应力松弛系数来考虑混凝土的徐变[13],应力松弛系数为
| $ \begin{array}{l} {K_r}\left( {t,\tau } \right) = 1 - \left( {0.2125 + 0.3786{\tau ^{ - 0.1458}}} \right) \times \\ \left\{ {1 - \exp \left[ { - 0.5464\left( {t - \tau } \right)} \right]} \right\} - \\ \left( {0.0495 + 0.2558{\tau ^{ - 0.0727}}} \right) \times \\ \left\{ {1 - \exp \left[ { - 0.{\rm{0156}}\left( {t - \tau } \right)} \right]} \right\}. \end{array} $ | (3) |
式中:t为计算时刻的混凝土龄期,d;τ为混凝土受荷时的龄期,d;(t-τ)为持荷时间,d.
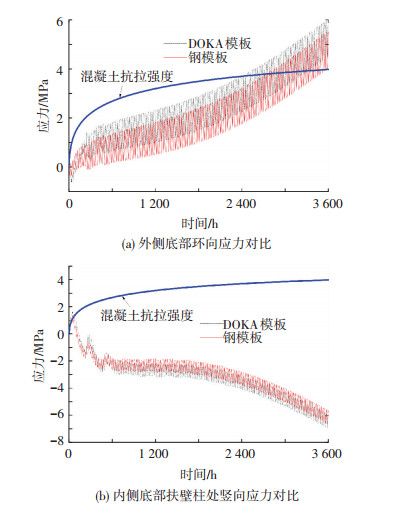
2 模板对结构温度应力的影响将文献[8]18 mm厚胶合木模板(导热系数0.837 kJ/(m·h·℃),比热1.8 kJ/(kg·℃)[14, 15])替换为5 mm的钢模板(导热系数258 kJ/(m·h·℃),比热0.48 kJ/(kg·℃))[16],施工期仍为5—9月.图 3是使用钢、木模板时的应力时程对比,可发现使用钢模板时罐壁各处的应力结果较使用木模板时有微幅降低,在模拟时间第3 600 h的降幅稳定在0.5 MPa左右.可见,钢模板对DOKA模板的替换虽然使LNG储罐混凝土外罐最不利位置的应力有所降低,但幅值很小,罐壁及扶壁柱处仍存在开裂现象.
|
图3 钢、木模板对应力结果的影响 |
混凝土收缩对温度应力的影响很大[8],而施工质量(包括养护条件、水灰比、骨料配比、振捣等)将对混凝土收缩起重要作用,因此可通过提高施工质量来控制混凝土的收缩,混凝土收缩可表示为[17]
| $ \varepsilon _y^T = \varepsilon _y^0 \cdot {M_1} \cdot {M_2} \cdots \cdot {M_n}\left( {1 - {e^{ - cr}}} \right), $ | (4) |
式中:εyτ为任意时间的收缩值,时间τ以d为单位;c为经验系数,取0.01;εy0为标准状态下的极限收缩值,本文取3.24×10-4;M1,M2,…,Mn为考虑各种非标准条件的修正系数,标准状态下取∏1nMi=1[17].
施工期仍设置在5—9月,但施工时通过提高施工质量以降低外罐混凝土的收缩值,即水灰比采用0.25(标准状态时水灰比为0.4),此时修正系数M4取0.75[17];同时采用蒸汽养护(标准状态为自然硬化),此时修正系数M9取0.85[17],在上述两项措施下:∏1nMi≈0.6,相当于对混凝土的收缩予以40%的折减.
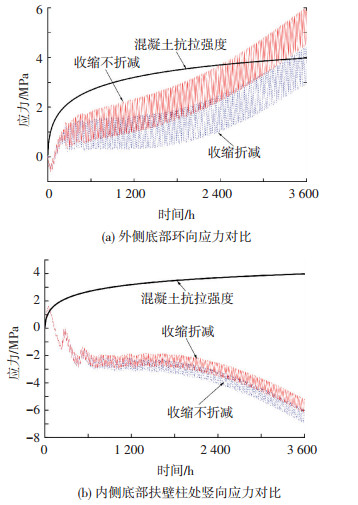
图 4为收缩值降低40%后LNG罐体的混凝土应力时程,结果显示:提高施工质量后,在施工时间3 600 h时,罐壁及扶壁柱处混凝土应力值降低明显,相当于混凝土收缩不折减情况的60%.
|
图4 施工质量对温度应力的影响 |
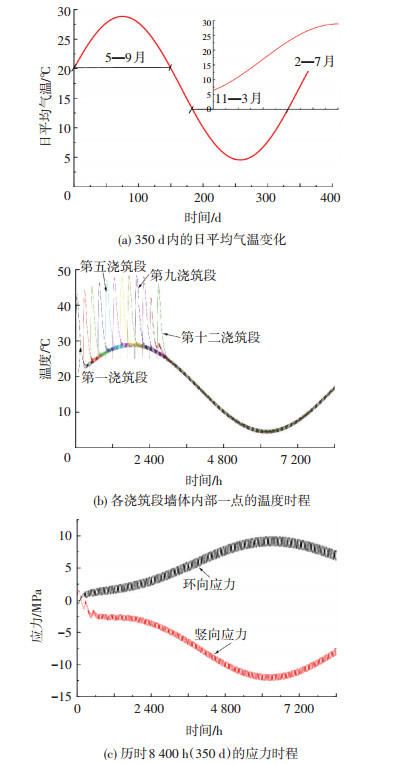
为了探讨外界气温变化对温度应力的影响,将计算模拟的时间延长到8 400 h(350 d),接近气温变化的1 a周期.图 5(a)是施工期间的日平均气温变化曲线;图 5(b)是各浇筑段墙壁内部一点的温度时程;图 5(c)是外侧底部环向应力时程和内侧底部扶壁柱处竖向应力时程.由图 5可得出最直观的结论就是混凝土环向应力变化曲线的凹凸与温度变化曲线的凹凸刚好相反,而竖向应力变化曲线的凹凸与温度变化曲线的凹凸一致.
|
图5 历时8 400 h(350 d)的应力时程 |
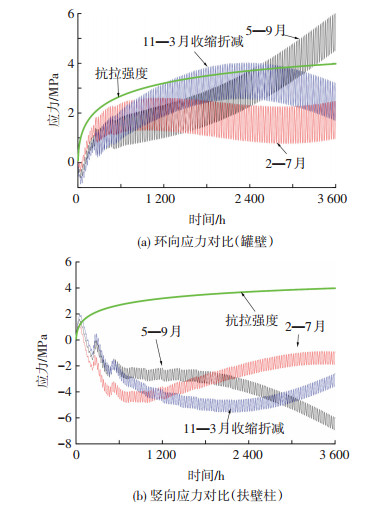
鉴于气温变化对温度应力的明显影响作用,本文考虑通过调整施工期来控制裂缝的产生.分3种季节情况:1)施工期为5—9月,入模温度为25 ℃;2)施工期为2—7月,入模温度为20 ℃;3)施工期为11—3月,同时考虑提高施工质量(即对收缩值折减40%),入模温度为10 ℃.上述入模温度的确定是根据施工期间的平均气温水平设定的.不同季节下的结构应力计算结果见图 6.
|
图6 不同施工季节的应力时程 |
为清楚了解外界气温对温度应力的影响,需要将图 6的结果同图 2中恒温考虑收缩条件下的应力曲线作比较.外界气温的变化导致混凝土的收缩与膨胀,由于收缩与膨胀受到约束而产生应力.在罐体的环向,外界气温降低时混凝土发生收缩,罐壁会产生环向拉应力;外界气温升高时混凝土发生膨胀,罐壁会产生环向压应力,即表现为图 6(a)中的环向拉应力曲线的凹凸与日平均气温变化曲线的凹凸相反.在罐体的竖向,可将罐体墙壁简化成悬臂结构,上部混凝土结构的收缩与膨胀变形,对于下部混凝土就如同外荷载作用,当外界气温降低时上部混凝土收缩,罐体内侧产生压应力,外侧产生拉应力;当外界气温升高时上部混凝土膨胀,罐体内侧产生拉应力,外侧产生压应力,表现为图 6(b)中的内侧底部扶壁柱处竖向应力曲线的凹凸与日平均气温变化曲线的凹凸一致.综上所述,混凝土环向应力变化曲线的凹凸与温度变化曲线的凹凸刚好相反,而竖向应力变化曲线的凹凸与温度变化曲线的凹凸要么一致,要么相反,视具体位置而定.
本文三组施工季节中,从应力时程与混凝土抗拉强度的对比出发,发现施工期设置在2—7月时,只有储罐罐体内侧底部扶壁柱处的早期竖向应力较大;而施工期设置在11—3月时,即使采取降低混凝土收缩量的改善措施,储罐罐壁外侧底部环向应力也在较早的时间就超过抗拉强度,出现开裂.因此本文认为合理安排施工季节对LNG储罐混凝土外罐温度应力的控制最为明显;提高混凝土的浇筑质量,控制混凝土的收缩,对控制裂缝的产生是有局限性的;合理利用施工期间外界气温的升温来抵制混凝土的收缩影响时(2—7月施工),没必要再提高混凝土的施工质量,即可控制裂缝的产生;当施工后期处于降温期(5—9月施工),可以利用提高浇筑质量,减少收缩来控制混凝土开裂(如图 4(a)所示,收缩折减后,环向应力降低);当施工前期处于降温段(11—3月施工),此时应力受混凝土收缩的影响较小,即使控制施工质量,降低了混凝土的收缩,也不能很好起到防裂作用.施工期可以理解为从开始施工到预应力张拉结束的这一段时间.
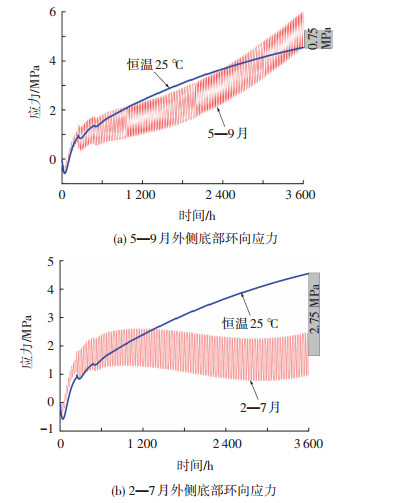
5 混凝土入模温度对结构受力的影响将混凝土刚入模的状态视为混凝土的初始状态,则入模之后外界气温与入模温度的差值决定混凝土的收缩与膨胀.以施工期间第150 d(即第3 600 h)的应力值进一步说明:5—9月施工期间第150 d的外界日平均气温值为20 ℃,比入模温度25 ℃低,等价于浇筑150 d后的混凝土会产生收缩,致使罐体产生环向拉应力,图 7(a)中的5—9月第150 d的拉应力平均值比恒温25 ℃条件下第150 d的拉应力值大0.75 MPa;2—7月施工期间第150 d的外界日平均气温值为28 ℃,比入模温度20 ℃高,等价于浇筑150 d后的混凝土会产生膨胀,致使结构产生环向压应力,图 7(b)中的2—7月施工期第150 d的拉应力平均值比恒温25 ℃条件下第150 d的拉应力值小2.75 MPa(施工模拟后期150 d时混凝土的弹性模量大致在20~30 GPa,线膨胀系数1×10-5/℃).另外,入模温度需尽量与施工期间的气温接近,以降低施工成本.
|
图7 入模温度对温度应力的影响 |
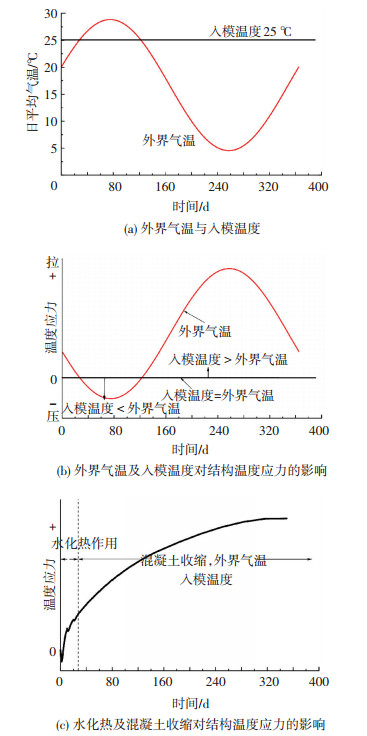
对于施工600 h以前的温度应力归因于水泥水化放热;而600 h以后的温度应力归因于混凝土收缩、外界气温及入模温度,其影响关系见图 8.图 8(c)显示600 h后收缩导致温度应力持续增长,但增长曲线斜率逐渐降低;图 8(b)中外界气温及入模温度导致温度应力呈Asin(ωt+φ)+B曲线变化(该图中温度应力曲线只为示意图形),其中Asin(ωt+φ)项由外界气温变化(施工季节)决定,其曲线变化趋势规律如第3节所述,而入模温度决定气温作用导致的温度应力的零应力值的位置(即常数项B):外界气温大于入模温度时,产生压应力;外界气温小于入模温度时,产生拉应力.由图 8(a)、(b)的对比可知,可以通过调节施工时间段(即正弦项的相位φ),使外界气温在施工前期处于升温状态,这样可将峰值应力的出现时间往后推,有利于控制裂缝的产生,因为经历的时间越长,混凝土的抗拉强度越高,同时后期预应力筋的布置可有效控制峰值拉应力,使其低于抗拉强度.
|
图8 温度应力影响因素分析 |
降低LNG储罐混凝土外罐施工期间拉应力的具体建议:(1)调整施工时间段,利用施工期间外界气温的逐渐提高来削弱混凝土收缩作用产生的拉应力增长;(2)如果施工期受限制,可提高养护质量,降低混凝土的收缩作用;(3)混凝土入模温度需考虑入模温度与施工后期气温的差值,如果施工后期气温处于下降段,则此差值宜为负.同时,入模温度的确定还需与施工期间的气温相宜,以降低施工成本.
7 结 论1)模板材料对储罐结构温度应力影响作用较小.
2)可通过调整施工时间段,利用外界气温的逐渐提高来降低混凝土收缩的不利影响.如果施工期有限制,可采取提高养护质量等措施,以降低混凝土的收缩作用.
3)入模温度的确定需考虑入模温度与施工后期的气温差值,如果施工期的后期气温处于下降段,则此差值宜为负.同时,入模温度还需与施工期间的气温相宜,以降低施工成本.
4)罐体内侧底部扶壁柱处的早期竖向应力,与混凝土的温升值和混凝土内外温差有关,而这两个温度值是负相关的,且任意一值较大都会导致较大的竖向拉应力致使开裂,为此,可采取局部分段施工来防止其开裂.
| [1] | BROOKE J J, AI-KAISI A F. Early strength development of protloand and slag cement concrete cured at eleveated temperature [J]. ACI Material Journal, 1990, 89(10): 503-507.( 1) 1) |
| [2] | EMBORG M, BERNANDER S. Assessment of risk thermal cracking in hardening concrete [J]. Journal of Structural Engineering, 1994, 120(10): 2893-2911.( 1) 1) |
| [3] | CERVERA M. Thermo-chemo-mechanical model for concrete: hydration and aging [J]. Journal of Engineering Mechanics, 1999, 125(9): 1018-1027.( 1) 1) |
| [4] | 肖明. 温变效应对大体积混凝土结构的损伤开裂分析[J]. 水力发电学报,1997, 57(2):8-18. ( 1) 1) |
| [5] | 朱伯芳. 不稳定温度场数值分析的分区异步长解法[J]. 水利学报,1995,26(8):46-52. ( 1) 1) |
| [6] | 王春. LNG储罐混凝土外罐早期温度裂缝分析[J]. 低温建筑技术,2009 (11): 119-120.( 1) 1) |
| [7] | 吴浩,卢云祥. 上海LNG储罐外罐的建造方案研究[J]. 中国水运,2008,8(1): 138-139.( 1) 1) |
| [8] | 翟希梅,王恒,周庆生,等. 大型LNG储罐混凝土外罐施工期间温度裂缝预测[J]. 石油学报,2013,34(4):780-786.( 4) 4) |
| [9] | 严跃兰,姚德新.广东天然液化气接收站DOKA模板施工技术[J]. 工程质量,2005,11(5):27-29.( 1) 1) |
| [10] | 关战伟. 基于ANSYS 平台增量法求解大体积混凝土早期弹性徐变温度应力[J]. 水科学与工程技术,2008(增刊2):83-85.( 1) 1) |
| [11] | 中华人民共和国住房和城乡建设部. 混凝土结构设计规范:GB 50010—2010[S]. 北京:中国建筑工业出版社,2010.( 1) 1) |
| [12] | 朱伯芳. 大体积混凝土温度应力与温度控制[M]. 北京:中国电力出版社,1999.( 1) 1) |
| [13] | 吴胜兴,周氐. 大体积混凝土温度应力松弛系数的优化确定[J]. 河海大学学报,1993,21(2):47-53.( 1) 1) |
| [14] | 黄潇,庞培培,刘艳. 混凝土结构中水化热产生温度应力的仿真分析[J]. 安徽建筑工业学院学报(自然科学版),2010,18(3):23-26.( 1) 1) |
| [15] | 刘唤. 大体积混凝土温度裂缝的仿真分析及其控制[D]. 邯郸: 河北工程大学,2013.( 1) 1) |
| [16] | 陈长华. 考虑钢筋作用的水工结构施工期温度场与温度应力分析[D]. 南京: 河海大学,2006.( 1) 1) |
| [17] | 王铁梦. 工程结构裂缝控制[M]. 北京:中国建筑工业出版社,1997:20-25.( 3) 3) |
 2016, Vol. 48
2016, Vol. 48


