2. 哈尔滨工业大学 土木工程学院, 150090 哈尔滨;
3.香港理工大学 土木与环境工程学院,999077 香港
2.School of Civil Engineering, Harbin Institute of Technology, 150090 Harbin, China;
3.Department of Civil and Environmental Engineering,The Hong Kong Polytechnic University, 999077 Hong Kong,China
钢管混凝土具有抗压承载力高、施工方便高效等优点,在桥梁结构中用作拱肋受力合理、造型美观.自1990年第一座钢管混凝土拱桥建成通车以来,这种桥型在中国发展十分迅速.对大跨径拱桥而言,采用桁式钢管混凝土拱肋更经济合理.中国2000年后建成的跨径超过150 m的54座钢管混凝土拱桥均采用了桁式拱肋结构.目前世界上跨度最大的上承式、中承式、下承式钢管混凝土拱桥也均采用桁式拱肋结构.
近年来,核心混凝土时效对大跨径钢管混凝土拱肋长期静力性能的影响日益受到工程界的关注.为此,研究人员针对正常使用阶段核心混凝土收缩徐变对钢管混凝土拱肋挠度[1, 2, 3, 4]、截面应力分布[1, 2, 3, 4]及内力分布[5]的影响进行了大量研究,但针对拱肋徐变稳定问题的研究较少.文献[6, 7, 8]对两端固定与(或)两端铰接的钢管混凝土圆弧深(浅)拱在径向均布持荷作用下的平面内徐变稳定问题进行了理论研究,但未考虑材料非线性的影响,尚不能满足设计需要;文献[9]对两座钢管混凝土拱桥的有限元分析发现准永久荷载组合所引起的拱肋核心混凝土徐变会使桥梁出平面稳定承载力降低5%~7%;文献[10, 11]对大长细比圆形截面钢管混凝土抛物线拱在均布荷载作用下的出平面徐变稳定问题进行了较为系统的参数分析,发现核心混凝土时效作用会使其稳定承载力最大降低14%.以上分析均未考虑施工过程,可能低估了时效作用对拱肋稳定性能的影响.
为此,本文同时考虑施工过程及核心混凝土时效作用影响,分析两端固定的四肢桁式钢管混凝土抛物线拱在沿跨度方向均布荷载作用下的出平面稳定性能.采用欧洲规范[12]EC2混凝土收缩徐变模型及逐步积分法模拟核心混凝土在变应力作用下的时效作用,采用文献[13]提出的应力-应变关系公式模拟高应力状态下核心混凝土的非线性性能及约束作用.以上材料性能通过UMAT二次开发程序引入ABAQUS中,建立较为精确的钢管混凝土拱肋长期静力性能有限元分析模型.研究由施工过程及核心混凝土时效作用所引起的拱肋屈曲前变形对钢管混凝土拱肋稳定承载力的影响.
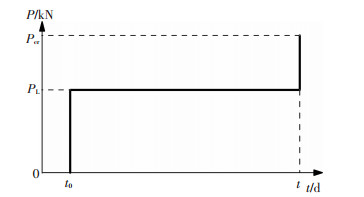
1 第一类与第二类徐变稳定混凝土时效作用所引起的结构或构件的稳定问题(又称结构或构件的徐变稳定问题)分为两类[14].第一类徐变稳定问题针对的是正常使用极限状态.结构或构件在准永久荷载组合作用下变形不断增加,应力状态不断改变,最终在某一时间点发生失稳.该时间点可称为临界时间.发生第一类徐变稳定问题时,作用于结构构件的持荷荷载等级一般较高,混凝土徐变可能呈现非线性特征(一般认为,当持荷应力超过混凝土强度的0.5倍时混凝土将发生非线性徐变[15]).以承受不变荷载为主(即不变荷载与可变荷载之比较高)的结构构件较易发生第一类徐变稳定问题.第二类徐变稳定问题针对的是承载力极限状态.结构或构件在突加(瞬时)荷载(如地震等可变荷载)作用下发生失稳,此时混凝土时效作用对结构或构件稳定承载力的影响在于在突加荷载施加前增加结构或构件的变形及改变其应力分布,从而降低其安全储备.以承受可变荷载为主(即不变荷载与可变荷载之比较低)的结构构件将发生第二类徐变稳定问题.对于第二类徐变稳定问题,结构或构件将经历两个荷载阶段:持荷阶段(对应正常使用极限状态)及突加荷载作用下的失稳阶段(对应承载力极限状态),见图 1.在持荷阶段,由于结构或构件内的应力水平较低,混凝土一般发生线性徐变;在第二阶段,突加荷载作用(无持荷时间)不会引起混凝土时效作用,因此在该阶段结构在突加荷载作用下仅发生瞬时变形.
|
图1 第二类徐变稳定问题加载过程 注:P表示所施加的荷载,PL为持荷荷载,Pcr为拱肋失稳时的荷载,t0为持荷荷载最初施加于构件时对应的时间,t为突加荷载施加时间. |
已有研究中,文献[6, 7, 8]对钢管混凝土拱的第一类徐变稳定问题展开研究,文献[9, 10, 11]针对的是钢管混凝土拱的第二类徐变稳定问题.对于大长细比钢管混凝土拱而言,其设计控制荷载一般为地震荷载组合[16],更易发生第二类徐变失稳.因此,本文针对大长细比四肢桁式钢管混凝土拱的第二类徐变稳定问题开展研究.
2 有限元分析模型 2.1 材料属性钢管混凝土拱肋在正常使用阶段核心混凝土内应力等级一般不超过0.5,此时混凝土应力-应变关系满足三点假设[17]:1)弹性应变为小应变;2)混凝土拉压向徐变特性相同;3)拱肋核心混凝土不考虑开裂.假设核心混凝土体积无穷大,采用EC2模型[12]模拟核心混凝土时效作用,其在变应力作用下的静力响应采用逐步积分法计算.具体材料本构及可靠性验证见文献[5, 18].
在突发荷载作用下,采用文献[13]提出的混凝土应力-应变曲线考虑高应力水平下混凝土材料非线性及约束作用,见式(1)、(2).该曲线虽然针对纤维模型法提出,但同样适用于梁单元有限元模拟[19].其中,时效作用的影响通过式(4)考虑[10].将混凝土本构通过UMAT二次开发引入ABAQUS.钢材的应力-应变关系采用五段式曲线模拟[13].
| $ \frac{{{\sigma _c}}}{{{\sigma _{c{\rm{r}}}}}} = 2\left( {\frac{{{\varepsilon _c}}}{{{\varepsilon _{cr}}}}} \right) + {\left( {\frac{{{\varepsilon _c}}}{{{\varepsilon _{cr}}}}} \right)^2},\frac{{{\varepsilon _c}}}{{{\varepsilon _{cr}}}} \le 1. $ | (1) |
| $ \frac{{{\sigma _c}}}{{{\sigma _{c{\rm{r}}}}}} = \left\{ \begin{array}{l} 1 + \eta \left[{{{\left( {\frac{{{\varepsilon _c}}}{{{\varepsilon _{cr}}}}} \right)}^{0.1\xi }} - 1} \right],\xi \ge 1.12,\frac{{{\varepsilon _c}}}{{{\varepsilon _{cr}}}} > 1;\\ \frac{{\left( {\frac{{{\varepsilon _c}}}{{{\varepsilon _{cr}}}}} \right)}}{{\beta {{\left( {\frac{{{\varepsilon _c}}}{{{\varepsilon _{cr}}}} - 1} \right)}^2} + \left( {\frac{{{\varepsilon _c}}}{{{\varepsilon _{cr}}}}} \right)}},\xi < 1.12,\frac{{{\varepsilon _c}}}{{{\varepsilon _{cr}}}} > 1. \end{array} \right. $ | (2) |
式中:σc与εc分别表示核心混凝土应力与应变,为考虑核心混凝土时效作用的影响,εc采用式(3)、(4)进行计算;σcr与εcr分别表示核心混凝土的峰值应力及对应的应变;ξ为约束系数;η与β为与约束系数及核心混凝土抗压强度有关的系数,具体计算方法见文献[13].
| $ \frac{{{\varepsilon _c}}}{{{\varepsilon _{cr}}}} = \frac{{\varepsilon - \Delta {\varepsilon _1}}}{{{\varepsilon _{cr}}}}, $ | (3) |
其中
| $ \Delta {\varepsilon _1} = {\varepsilon _1} + {\varepsilon _{cr}} - {\varepsilon _{cr}} \cdot \sqrt {1 + \frac{\sigma }{{{\sigma _{cr}}}}} . $ | (4) |
式中:ε表示当前核心混凝土应变; ε1与σ1分别表示突加荷载施加前核心混凝土的应变与应力,由EC2模型确定.
2.2 单元类型建模时不考虑钢管与混凝土间的相对滑移,在两节点之间建立两根B31型铁木辛柯梁单元,分别赋予钢管与核心混凝土的材性及截面形状.该模拟方法可保证两单元在节点处变形协调,从而实现了钢管混凝土构件的平截面假定.拱肢间的空心钢腹杆选用T3D2型杆单元模拟.
2.3 边界条件与荷载在拱脚处限制所有单元在全部方向的位移及转角.将均布荷载折算成集中力施加于节间节点上.钢管内核心混凝土灌注过程采用ABAQUS中单元移除(remove)、激活(add)予以实现.激活时,将梁单元设为无应变状态.分析时忽略空钢管吊装过程的影响,将空钢管合龙作为施工初始步,相关的可行性论证见文献[20].
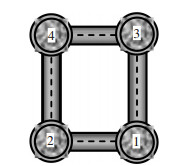
3 参数分析 3.1 基本参数对四肢桁式钢管混凝土抛物线拱的出平面徐变稳定性能进行参数分析,其截面形式见图 2.
|
图2 四肢桁式钢管混凝土截面形式 |
参考典型四肢桁式钢管混凝土拱桥拱肋设计方案,拱肋跨度取为100 m,跨矢比l/f=5,拱肋沿跨度方向等分为40个节间.上弦杆、下弦杆钢管直径为0.5 m,拱肋钢管壁厚由含钢率确定.拱肢间的空心钢腹杆直径为0.3 m,壁厚统一取7.5 mm.钢管选用Q345钢材,弹性模量为2.0×105 MPa,内灌C50混凝土.拱肋核心混凝土的灌注分4步完成,每隔2 d灌注1根钢管,灌注顺序见图 2.当混凝土龄期达到28 d时(t0=28 d),对拱肋施加相当于运营阶段所承受的准永久荷载组合作用的荷载值,持荷100 a后(t-t0=100 a),瞬时加载直至破坏.考虑参数包括:长细比(拱弧长与截面惯性矩的比值la/ky)为150、200、250;含钢率(α)为4%、8%、12%;荷载等级(长期荷载与瞬时承载力比值PL/Pcro)为0.5、0.7.
|
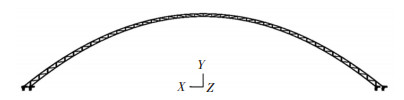
图3 有限元模型 |
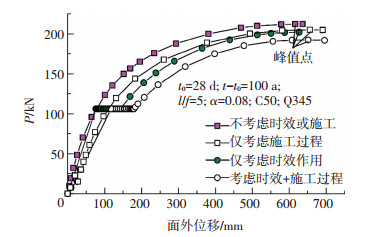
图 4分析了时效作用、施工过程及两者共同作用对长细比为250、截面含钢率为8%的四肢桁式钢管混凝土拱稳定性能的影响.各曲线峰值点均已在图中标出.可见,施工过程及时效作用所引起的拱肋屈曲前变形均会降低拱肋稳定承载力,其中,施工过程可使拱肋稳定承载力降低3.4%,时效作用可使其降低4.8%,而同时考虑两者的影响时,拱肋稳定承载力降低10.1%.可见,对于本算例,仅考虑时效作用或仅考虑施工过程的影响时,拱肋稳定承载力的降低幅度均较小(<5%),但当同时考虑两者作用时,拱肋稳定承载力降低幅度达10%,设计中应予以考虑.
|
图4 典型四肢桁式拱肋荷载-拱顶位移曲线 |
时效作用对钢管混凝土拱肋稳定承载力的影响由两方面引起,一方面,时效作用引起拱肋位移的增加,加剧在竖向荷载作用下的二阶效应,进而影响拱肋稳定性;另一方面,时效作用导致钢管应力增加,使其提前进入塑性,降低钢管对拱肋稳定承载力的贡献.施工过程会对钢管混凝土拱肋稳定承载力造成影响主要是由于核心混凝土灌注完毕前拱肋刚度偏低,导致较大的拱肋位移因而加剧了二阶效应;同时,拱肋灌注完毕前,钢管是主要的受力构件,相对于不考虑施工过程的分析结果,其截面内实际应力水平较高,会提前进入塑性退出工作;此外,在拱肋核心混凝土的灌注过程中拱肋截面刚度中心与几何中心不重合,荷载作用存在初偏心,时效作用导致该偏心距发生变化,也会降低拱肋稳定承载力.
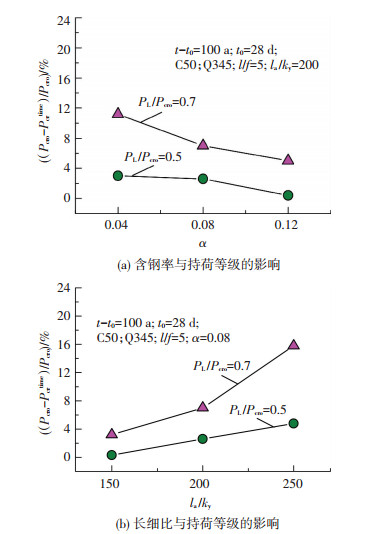
仅考虑时效作用的影响,对不同参数的四肢桁式钢管混凝土拱的稳定性能进行分析,并将计算所得拱肋稳定承载力(Pcrtime)与不考虑施工过程与时效作用影响计算所得拱肋稳定承载力(Pcro)进行对比,降低幅度见图 5.
|
图5 仅时效作用引起的拱肋稳定承载力降低幅度 |
由图 5可看出,时效作用所引起的屈曲前变形使四肢桁式钢管混凝土拱肋的稳定承载力有所降低,降低幅度随含钢率的降低、拱肋长细比的增加或长期荷载等级的提高而增大.对于长细比为200的拱肋,在0.7Pcro的持荷荷载作用100 a后,含钢率为12%的拱肋稳定承载力仅降低5.0%,但当含钢率降至4%时,该降低幅度达到11.2%(图 5(a)).相同的持荷荷载作用使长细比为150、含钢率为8%的拱肋稳定承载力降低3.2%;而使长细比为250的同含钢率拱肋承载力降低15.8%(图 5(b)).
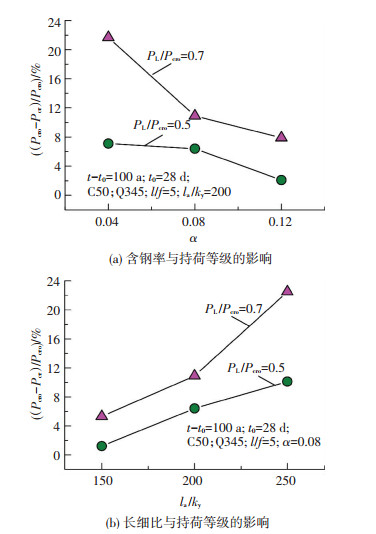
兼顾施工过程、时效作用两方面的影响后,对不同参数的四肢桁式钢管混凝土拱的稳定性能进行分析,并将计算所得稳定承载力(Pcr)与不考虑施工过程与时效作用影响计算所得拱肋稳定承载力(Pcro)进行对比,降低幅度见图 6.比较图 5、6可见,兼顾时效作用和施工过程的四肢桁式钢管混凝土拱出平面稳定承载力降低幅度随长细比、含钢率、荷载等级的变化规律与仅考虑时效作用时相似,但幅度显著增大.
|
图6 兼顾施工过程与时效作用后拱肋稳定承载力降低幅度 |
含钢率越低,施工过程对拱肋出平面徐变稳定承载力的影响越显著.当PL=0.7Pcro时,对于长细比为200、含钢率为4%的钢管混凝土拱肋而言,不考虑施工过程时,时效作用使其稳定承载力降低11.2%,考虑施工过程后,降低幅度增至21.7%,是原有降低幅度的近二倍;而含钢率达到12%时,两者仅相差58%.
4 结 论1)时效作用所引起的屈曲前变形使四肢桁式钢管混凝土拱肋的稳定承载力显著降低,最大可达15.8%.其降低幅度随含钢率的降低、拱肋长细比的增加或长期荷载等级的提高而增大.
2)兼顾时效作用与施工过程影响后,四肢桁式钢管混凝土拱的出平面稳定承载力降低幅度变化规律与仅考虑时效作用时相同,但幅度显著增大,在本文分析参数范围内,最大可降低22.5%,可见时效作用与施工过程的影响不容忽视,在设计中应予以考虑.
3)含钢率越低,施工过程对四肢桁式钢管混凝土拱出平面徐变稳定承载力的影响越显著.
| [1] | 张治成. 大跨度钢管混凝土拱桥的徐变分析[J]. 工程力学, 2007, 24(5): 151-160. ( 1) 1) |
| [2] | SHAO Xudong, PENG Jianxin, LI Lifeng, et al. Time-dependent behavior of concrete-filled steel tubular arch bridge [J]. Journal of Bridge Engineering, 2010, 15(1): 98-107.( 1) 1) |
| [3] | WANG Yuanfeng, HAN Bing, DU J S, et al. Creep analysis of concrete filled steel tube arch bridges [J]. Structural Engineering and Mechanics, 2007, 27(6): 639-650.( 1) 1) |
| [4] | GENG Yue, WANG Yuyin, RANZI G, et al. Time-dependent analysis of long-span concrete-filled steel tubular arch bridges [J]. Journal of Bridge Engineering, 2014, 19(4): 04013019.DOI:10.1061/(ASCE)BE. 1943-5592.0000549.( 1) 1) |
| [5] | 耿悦,吴欣荣,王玉银. 施工过程对钢管混凝土桁式拱桥长期静力性能的影响 [J]. 建筑结构学报, 2013, 34(增刊 1): 52-58. ( 2) 2) |
| [6] | 王玉银, 刘昌永, 张素梅. 铰接圆弧钢管混凝土拱平面内徐变稳定[J]. 工程力学, 2011, 28(3): 198-204. ( 2) 2) |
| [7] | BRADFORD M A, PI Y L, QU W L. Time-dependent in-plane behaviour and buckling of concrete-filled steel tubular arches [J]. Engineering Structures, 2011, 33(5): 1781-1795.( 2) 2) |
| [8] | PI Y L, BRADFORD M A, QU W L. Long-term non-linear behaviour and buckling of shallow concrete-filled steel tubular arches [J]. International Journal of Non-linear Mechanics, 2011, 46(9): 1155-1166.( 2) 2) |
| [9] | 黄永辉. 钢管混凝土拱桥拱肋病害机理与影响分析及吊杆更换技术研究 [D]. 广州:华南理工大学,2010:137.( 2) 2) |
| [10] | 王玉银, 吴欣荣, 耿悦, 等. 均布荷载作用下钢管混凝土拱长期稳定性能分析[J]. 建筑钢结构进展, 2011, 13(6): 31-35. ( 3) 3) |
| [11] | GENG Yue, WANG Yuyin, WU Xinrong, et al. Out of plane creep buckling analysis on cfst arches[C]// EUROSTEEL 2014. Naples, Italy: ECCS European Convention for Constructional Steelwork, 2014:531-532.( 2) 2) |
| [12] | BS EN 1992-1-1. Eurocode 2: Design of concrete structures part 1-1: general rules and rules for buildings [S]. London: BSI, 2004.( 2) 2) |
| [13] | 韩林海. 钢管混凝土结构-理论与实践[M].2版. 北京:科学出版社, 2007.( 4) 4) |
| [14] | BAZANT Z P, CEDOLIN L. Stability of structures: elastic, inelastic, fracture, and damage theories[M]. Mineola, New York :Dover Publications INC,2003.( 1) 1) |
| [15] | GILBERT R I, RANZI G. Time-dependent behaviour of concrete structures [M]. London: Spon Press, 2011.( 1) 1) |
| [16] | 崔军. 大跨度钢管混凝土拱桥受力性能分析[D]. 杭州:浙江大学,2003. ( 1) 1) |
| [17] | CEB (Comité Euro-International du Béton). CEB design manual on structural effects of time-dependent behavior of concrete [M]. Saint-Saphorin, Switzerland: Georgi Publishing, 1984:77-80.( 1) 1) |
| [18] | GENG Yue, RANZI G, WANG Yuyin et al. Time-dependent behaviour of concrete-filled steel tubular columns: analytical and comparative study [J]. Magazine of Concrete Research, 2012, 64(1):55-69.( 1) 1) |
| [19] | HAN Linhai, YANG Hua, CHEN Shuliang. Residual strength of concrete filled RHS stub columns after high temperatures [J]. Advances in Structural Engineering, 2002 (5): 123-133.( 1) 1) |
| [20] | GENG Yue, ZHANG Sumei, WANG Yuyin, et al. Static behaviour of a concrete filled steel tubular double X-shape arch bridge without wind braces under construction [C]//Proceeding of 9th Pacific Structural Steel Conference.Beijing: China Architecture and Building Press, 2010:906-910.( 1) 1) |
 2016, Vol. 48
2016, Vol. 48


