型钢-混凝土组合柱(SRC)是指在钢筋混凝土柱(RC)内配置型钢，通过型钢分担部分轴力提高极限承载力，同时内置型钢限制剪切裂缝的发展，改善柱的延性，有效提高其抗震性能^{[1, 2]}.日本、前苏联、美国、欧洲等对SRC柱的理论计算研究较为成熟^{[3, 4, 5, 6]}.中国《钢骨混凝土结构设计规程》和《型钢混凝土组合结构技术规程》分别通过叠加原理和极限状态法建立了SRC柱承载力计算式^{[7, 8]}.随着高强钢(屈服强度≥460 MPa)生产工艺的提高，将高强钢应用于SRC柱将大幅提高其极限承载力，例如北京鸟巢采用Q460高强钢板进行设计^[9]，河南省某超高层项目使用Q460高强钢对结构进行优化设计^[10].目前国内学者对高强钢结构的受力性能已有一定研究成果^{[11, 12]}，而高强钢SRC柱的力学性能研究鲜见报道.

本文通过试验和有限元方法研究Q460高强钢SRC柱在小偏心作用下的承载力、破坏方式和破坏机理.通过有限元参数分析评价了屈服强度和含钢率对SRC柱承载力的影响.通过叠加法和N-M相关曲线研究传统理论方法针对SRC柱偏压承载力计算的适用性.

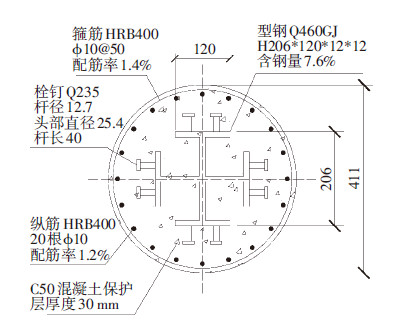
试件截面尺寸参考上述“河南省某超高层项目”应用的第53层SRC柱设计，采用相似比为1:3的缩尺模型.缩尺模型高1 900 mm，其含钢量、钢筋配筋率以及栓钉焊接方法见图 1.试件制作同时，预留出用于材性试验的试件，各材料的力学性能平均值见表 1.

图1(Figure 1)

图1 SRC柱截面示意

表1(Table 1)

表1 材料力学性能 材料 屈服强度 fy /MPa 极限强度 fu /MPa 抗压强度 fcu /MPa 伸长率 δ/% Q460GJ钢板 516.7 635.4 — 28.1 Φ10钢筋 426.0 605.5 — — 混凝土 — — 46.8 —

表1 材料力学性能

试验在大型拟静力结构卧式试验机上进行.荷载通过小刚性垫块传递，偏心距120 mm.考虑实际工程中组合柱受到轴力、弯矩和剪力的共同作用，试件底部采用高强螺栓与反力架底座连接，实现刚接，柱顶通过试件与垫块的摩擦力约束平动位移，实现铰接.试验加载方式和位移计布置见图 2.试验得到SRC柱极限承载力分别为7 574、7 318 kN.

图2(Figure 2)

图2 加载方式及位移计布置示意

采用ABAQUS有限元软件建立有限元模型.混凝土、型钢以及钢筋分别采用实体单元、曲壳单元以及桁架单元.横截面划分网格25 mm每单元，柱高方向55 mm每单元.型钢及钢筋采用嵌入式与混凝土变形协调，忽略相互间的滑移.

混凝土采用塑性损伤模型，本构关系参考规范GB 50010—2010^[13]，钢材采用理想弹塑性本构模型.荷载施加在传力钢垫板上以防止柱顶应力集中.柱底设置平动约束和转动约束，柱顶设置平动约束.

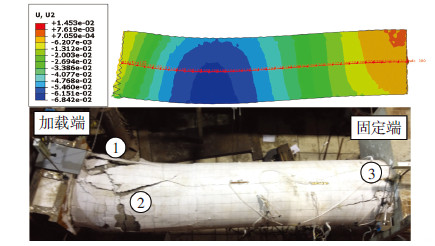
有限元结果见图 3，荷载-位移曲线与试验结果基本吻合.极限承载力为7 372 kN，与试验结果分别相差2.7%和0.8%.如图 4所示，SRC柱破坏时，有限元侧向位移云图表明柱体变形最大位移靠近加载端，与试验的变形模态一致.

图3(Figure 3)

图3 SRC柱荷载-轴向位移曲线

图4(Figure 4)

图4 试验与有限元破坏示意

由图 3所示的位移-荷载曲线，破坏过程分5个阶段：(1)弹性阶段，曲线近似直线，柱体无开裂现象.(2)弹塑性阶段，荷载比达到约0.25后，SRC柱刚度降低，加载端偏压侧出现微裂缝，裂缝宽度逐渐增大、数量增多，见图 5.(3)塑性阶段，荷载比达到约0.83后，曲线出现明显转折，压区混凝土不断压溃，柱体有明显侧向变形，SRC柱带裂缝工作，反映出一定的塑性性能.(4)曲线达到峰值，SRC柱达到破坏，承载力下降，加载端混凝土压溃，出现斜裂缝和多条横向裂缝，SRC柱发生纵向弯曲破坏，见图 6.(5)破坏阶段，组合柱仍具有一定的承载能力，表明高强钢骨提高了SRC柱的承载和变形能力.

图5(Figure 5)

图5 弹塑性阶段柱体裂缝

图6(Figure 6)

图6 破坏阶段柱体裂缝

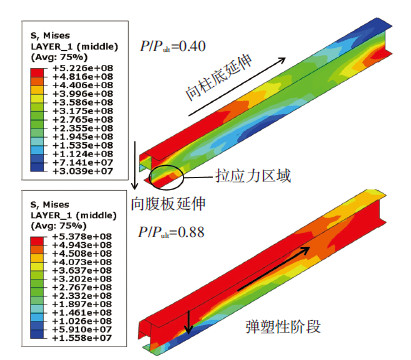
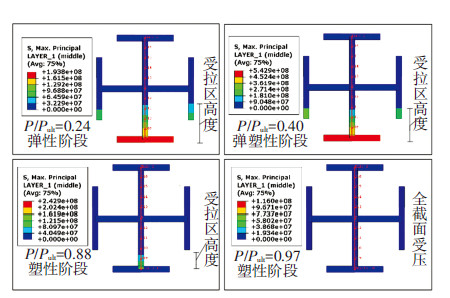
弹性阶段，RC部分未达到抗压强度，压应力较为集中分布于柱顶，钢骨应力远小于屈服强度.弹塑性阶段，由于加载端混凝土压溃失效，承压区域转移，压应力集中分布于柱体中部，见图 7；钢骨端部承担部分压力而应力集中，且应力向柱底发展，见图 8.塑性阶段至SRC柱破坏，钢骨大部分截面屈服，塑性变形不断发展，直至构件破坏.

图7(Figure 7)

图7 弹塑性阶段混凝土剖面应力分布云图

图8(Figure 8)

图8 弹塑性阶段钢骨剖面应力分布云图

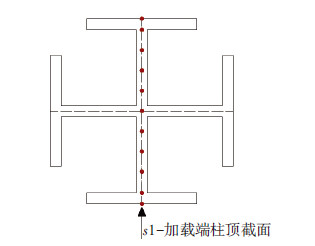
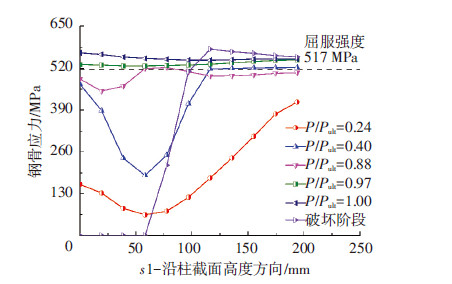
选取沿柱截面径向路径s1，见图 9，分析加载过程中钢骨截面受拉受压侧应力变化规律.如图 10、11所示，随着荷载增加，截面受拉区高度不断减小，截面中和轴下移，塑性阶段时s1截面已全部受压，钢骨端头局部压曲，应力减小，破坏后钢骨端部变形过大而失去承载能力，应力为零.

图9(Figure 9)

图9 应力测点布置示意

图10(Figure 10)

图10 各阶段s1截面的主拉应力分布

图11(Figure 11)

图11 各阶段s1截面应力分布

本文结合工程实际重点研究型钢材屈服强度和含钢率(翼缘厚度、腹板厚度)对SRC柱小偏压承载力的影响.屈服强度分别取235、345、390、460、550和690 MPa(及试验值517 MPa).钢骨翼缘、腹板厚度根据《钢结构设计规范》^[14]宽厚比、高厚比限值规定取值，见表 2.

表2(Table 2)

表2 含钢率(钢骨翼缘、腹板厚度)参数 翼缘厚度/ mm 含钢率/ % 宽厚比 腹板厚度/ mm 含钢率/ % 高厚比 注：翼缘(腹板)厚度变化时，腹板(翼缘)厚度均为12 mm. 6.0 5.5 9.0 5.0 5.7 36.4 8.5 6.4 6.4 8.4 6.6 21.7 12.0 7.5 4.5 16.5 8.7 11.0 20.0 10.1 2.7 20.0 9.5 9.1

表2 含钢率(钢骨翼缘、腹板厚度)参数

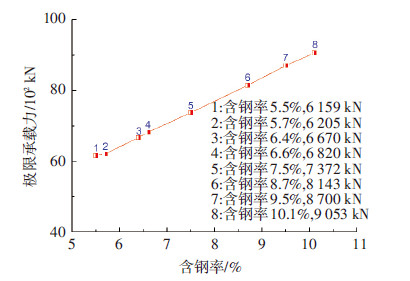
偏压承载力与屈服强度和含钢率基本呈线性关系，见图 12、13.采用Q460高强钢SRC柱相比Q235普通钢SRC柱承载力提高近42%.采用大厚度钢板同样能提高承载力，但钢板较厚会降低混凝土的浇捣质量，因此通过采用高强钢既能保证SRC柱的承载能力又能有效控制截面尺寸，避免不利于抗震的短柱结构.

图12(Figure 12)

图12 屈服强度对SRC柱承载力的影响

图13(Figure 13)

图13 含钢率对SRC柱承载力的影响

日本学者若林实^[15]提出一般叠加法计算SRC柱正截面压弯承载力，将其表示为钢骨和RC部分的简单叠加，见式(1).该方法任意分配钢骨和RC部分的轴力，通过反复试算得到受弯承载力之和的最大值，过程较为复杂.

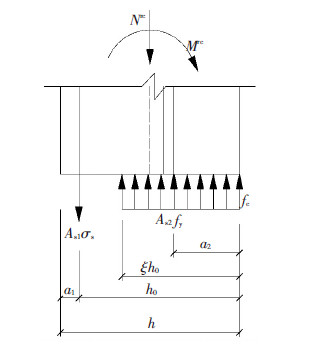
李少泉等^[16]给出一般叠加公式的解析解，有效简化计算过程.由SRC柱钢骨部分承担的N^ss-M^ss相关关系式(2)、(3)，并按小偏压考虑，钢骨截面受压(N^ss≥0)见图 14，钢骨部分弯矩表示为式(4)，RC部分力和弯矩平衡方程为式(5)、(6).

图14(Figure 14)

图14 小偏压作用下RC部分正截面受力图

圆截面SRC柱按照等效矩形概念，将bh₀等效为圆截面受压区面积A_c，如式(8).代入式(5)、(6)得到新的平衡方程式(9)、(10).

将式(9)、(10)代入叠加方程(1)，得到弯矩M为轴力N^rc的二次式.令$\frac{{{\rm{d}}M}}{{{\rm{d}}{N^{{\rm{rc}}}}}} = 0$，得到SRC柱弯矩最大时的轴力N^rc，并由M=Ne，得到偏心距为120 mm时，SRC柱截面小偏压极限承载力为7 463 kN，与试验结果分别相差1.4%和1.9%.

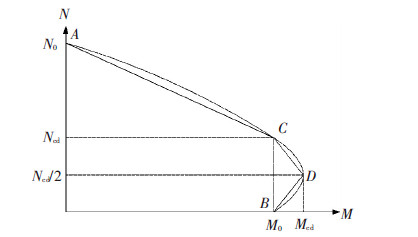
欧洲规范EC4^[6]基于相对长细比概念，考虑材料弹塑性和几何非线性，以组合柱同时承担轴力和弯矩的相关关系(N-M曲线)作为失效条件计算压弯承载力，见图 15.多边形ACDB为近似N-M曲线的简化，点D为大、小偏心受压界限点.

图15(Figure 15)

图15 N-M相关曲线

各点含义见图 16，其中，SRC柱截面受弯区域高度假设为2h_n，且处于钢骨腹板位置.根据平衡条件得到各点轴力和弯矩绘制N-M曲线.偏心距为120 mm的偏压承载力计算值6 614 kN，与试验结果分别相差12.6%和9.6%.

图16(Figure 16)

图16 欧洲规范计算截面示意

表 3、4为参数范围内理论结果与有限元结果对比.“叠加法的解析解”的理论结果与有限元结果相比差值小于5%，计算精度高；“N-M相关曲线方法”理论值偏小，且随着屈服强度的提高，理论结果差值越大，达到10%~20%，结果过于保守.

表3(Table 3)

表3 屈服强度参数理论结果与有限元结果 型钢屈强 fss/Mpa FEM P0/kN 叠加法 P1/kN 差值 δ1/% N- M曲线 P2/kN 差值 δ2/% 235 4 846 4 561 -5.80 4 797 -1.00 345 5 912 5 703 -3.54 5 511 -6.78 390 6 303 6 166 -2.17 5 815 -7.74 460 6 873 6 884 0.16 6 218 -9.53 550 7 675 7 802 1.65 6 878 -10.38 690 8 854 9 225 4.19 7 756 -12.40

表3 屈服强度参数理论结果与有限元结果

表4(Table 4)

表4 含钢率参数理论结果与有限元结果 含钢率/% FEM P0/kN 叠加法 P1/kN 差值 δ1/% N- M曲线 P2/kN 差值 δ2/% 注： δn=(Pn-P0)/P0×100% 5.5 6 159 5 977 -2.96 5 300 -13.95 5.7 6 205 6 367 2.61 5 752 -7.30 6.4 6 670 6 576 -1.41 5 930 -11.09 6.6 6 820 6 894 1.09 6 276 -7.98 7.5 7 372 7 463 1.23 6 614 -10.28 8.7 8 143 8 178 0.43 6 944 -14.72 9.5 8 700 8 731 0.36 7 176 -17.52 10.1 9 053 9 439 4.26 8 222 -9.18

表4 含钢率参数理论结果与有限元结果

1)高强钢SRC柱在小偏压作用下发生纵向弯曲破坏.受力过程中，柱顶偏压侧混凝土压溃，钢骨承担更多轴力的同时限制剪切裂缝发展，组合柱表现出良好的延性和变形能力.

2)有限元分析得到组合柱钢骨翼缘和腹板的应力分布和变化规律.参数分析结果表明，采用高强度结构钢更利于在提高SRC柱承载力的同时，控制钢材用量和截面尺寸，减轻结构自重.

3)采用两种理论对SRC柱小偏压作用下极限承载力值进行计算.结果表明，叠加法计算较为复杂，但结果较为准确；N-M相关曲线法概念简单，但计算结果偏于保守.