工业及海洋大气环境下钢结构极易产生腐蚀,腐蚀将改变钢材的几何和力学特性,致使构件性能退化,承载力及刚度降低,导致结构在偶遇荷载作用下更易发生破坏,严重影响结构的耐久性.虽然,国内外学者对钢材腐蚀进行了大量研究,但是大多仅停留在材料层面:文献[1]通过对4种不同腐蚀环境下的钢板进行拉伸试验,分别研究了锈蚀钢材各项力学性能指标的退化规律;文献[2, 3]采用有限元模拟和试验的方法,讨论了点蚀尺寸参数对锈蚀钢材屈服强度、极限强度的影响规律.
目前,关于腐蚀环境下钢构件承载性能的研究有了一定进展:文献[4, 5]研究了腐蚀环境下影响锈蚀受弯构件承载性能的主要因素;文献[6]通过对等边角钢试件进行拟静力试验,发现腐蚀损伤使得构件承载力和刚度显著减小,延性和耗能能力降低;文献[7]通过对多根电化学腐蚀下的角钢进行抗压承载性能试验,得到了角钢锈蚀与其抗压承载力之间的关系.
腐蚀对压弯构件的影响主要体现在两方面:截面面积损耗和材料力学性能退化.本文从以上两个角度出发,对锈蚀钢材偏心受压柱的整体稳定受力性能退化规律展开研究.通过对7根H型钢构件进行最长达3 a的自然暴露盐雾加速腐蚀试验以及偏心受压整体失稳承载力试验,讨论了锈蚀钢柱的各项整体稳定承载性能参数随锈蚀率的变化趋势,分析了腐蚀损伤导致偏心受压钢柱承载性能发生劣化的原因,并结合有限元数值计算分析确定了整体稳定承载力和塑性发展系数随锈蚀率的退化规律.
1 试验概况 1.1 H型钢构件加速腐蚀试验金属材料在自然环境下的暴露腐蚀试验是大气腐蚀最通常的试验方法,与大气腐蚀试验相比,室内加速腐蚀试验周期较短,但由于考虑的腐蚀因素不够全面,与真实腐蚀过程的相关性较差[8, 9].为了在较短的试验周期内较好地重现钢材在海洋大气环境下的腐蚀形态,采用中性盐雾喷淋的方法对暴露于室外的型钢构件进行加速腐蚀.
首先将7根截面尺寸为HW125×125×6.5×9的Q235热轧H型钢构件放置于西安建筑科技大学土木楼楼顶,构件长度均为2 000 mm;然后定期在构件表面均匀喷洒体积分数18%的NaCl溶液进行加速腐蚀.为保证构件翼缘和腹板的腐蚀条件一致,将各个试件的两侧翼缘与地面垂直放置,并且每隔4~5 d翻转一次,锈蚀周期为3 a.
1.2 材性试验在中性盐雾腐蚀环境下,钢材表面易产生大量大小不均的点蚀坑,导致锈蚀后钢材的强度和延性发生退化.为此,在进行锈蚀钢柱偏压承载力试验之前需进行材性试验,研究腐蚀环境作用下Q235钢材的锈蚀程度及力学性能参数退化规律.
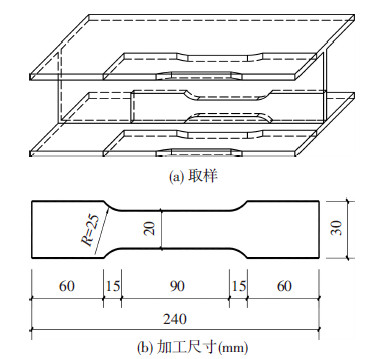
加速腐蚀试验结束后,从每根锈蚀H型钢一端切取长度400 mm试件,然后分别从翼缘和腹板部分截取材性试验所需试件进行酸洗除锈、烘干并称重,然后按照《金属材料拉伸试验第1部分:室温试验方法》[10]相关规定在CSS-WAW300DL型电液伺服万能试验机上进行材性试验,试件取样及加工尺寸见图 1.
|
图1 试件取样及加工尺寸 |
为研究锈蚀后偏心受压钢柱的整体稳定性能退化规律,将试验试件分为两组,A组为上述7根加速腐蚀H型钢柱,长度为1 600 mm;B组则为2根相同材质和规格的未锈蚀H型钢柱,用作对比试验.为避免试验误差和加载方式对试验结果的影响,在所有试件两端均设置端板和加劲肋,端板与加劲肋尺寸分别为20 mm×250 mm×250 mm和10 mm×150 mm×50 mm.柱与端板、柱与加劲肋之间均采用角焊缝连接,焊脚尺寸和焊缝长度满足强度要求.
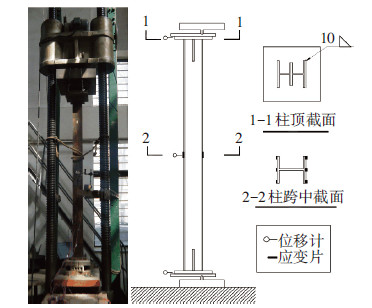
本次试验在2 000 kN的YE-200A型压力试验机上进行,由于试验设定为强轴平面内弯曲的单向偏心偏压试验,偏心距为58 mm,柱两端为铰接约束,因此,根据文献[11]建议,采用单刀刀口铰支座进行加载,且刀口摆放方向与受压翼缘中心线相吻合,见图 2.为准确测量锈蚀压弯构件整体失稳破坏过程中试件跨中挠度,在构件跨中和上下两支座处各设置一个位移计,测量压弯面内弯曲挠度;在试件中部上下翼缘处各布置3片应变片,用于监测压弯构件跨中截面在加载过程中的应变状态.
|
图2 加载装置示意 |
压弯试验开始正式加载时,荷载应分级施加,每级施加荷载约为预计承载力的1/10,加载到7级或8级后,切换每级施加荷载为预计承载力的1/20直至荷载不能继续增加,当试件达到极限荷载且随后荷载出现显著下降(降至极限荷载的80%以下)时停止试验.
2 结果及分析 2.1 锈蚀钢材力学性能试验结果及分析锈蚀钢材的力学性能退化直接影响压弯构件的承载性能,因此着重对钢材屈服强度fy、抗拉强度fu,以及伸长率δ随锈蚀率的退化规律进行研究,钢材锈蚀率定义为
| $\eta=\left({{m}_{0}}-m \right)/{{m}_{0}},$ | (1) |
式中:η为锈蚀率,m0为腐蚀前试件理论重量,即按照锈蚀前型钢规格厚度、密度计算的试件重量,m为腐蚀后试件实际重量.
表 1给出了锈蚀钢板试件力学性能试验结果,发现随着锈蚀程度的不断加深,钢材的屈服强度、极限强度和伸长率均出现不同程度的下降.
| 表1 材性试验结果 |
根据表 1所列试验数据,分别建立屈服强度比、极限强度比及伸长率比与锈蚀率之间的定量关系:
| $f_{^{y}}^{'}/{{f}_{y}}=1-0.235\eta,$ | (2) |
| $f_{u}^{'}/{{f}_{u}}=1-0.309\eta,$ | (3) |
| $\delta '/\delta=1-2.96\eta+4.08{{\eta }^{2}}.$ | (4) |
式中:fy、 f ′y、为未锈蚀和锈蚀钢材的屈服强度,fu、f ′u为未锈蚀和锈蚀钢材的极限强度,δ、δ′为未锈蚀和锈蚀钢材的伸长率.
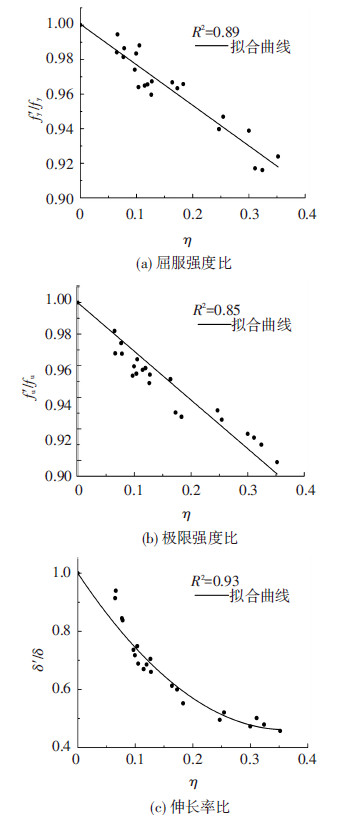
各表达式与试验数据的拟合情况见图 3.屈服强度比和极限强度比均随着锈蚀率的增大呈线性下降趋势,且极限强度比的退化现象更为明显,说明腐蚀使得钢材的应变硬化效应逐渐减弱;伸长率比随着锈蚀率的增大呈二次曲线下降趋势,说明锈蚀钢材的延性逐渐劣化,而脆性性能随之产生.
|
图3 锈蚀钢材力学性能参数与锈蚀率的关系 |
对A、B两组H型钢柱试件进行偏压承载力试验,见图 4.锈蚀试件破坏形态与未锈蚀试件相比没有发生明显变化,仍为压弯平面内的整体失稳破坏.通过对两组试件跨中截面翼缘处应变进行监测,发现试件失稳时只有受压翼缘进入塑性,随着锈蚀程度的不断加深,极限荷载对应的受压翼缘应变急剧下降,当锈蚀率从0%增长至24.68%时,极限应变从0.002 393降至0.001 693,说明腐蚀严重限制了跨中截面在极限状态下的塑性发展,导致压弯试件的承载性能退化.

|
图4 试件破坏模式 |
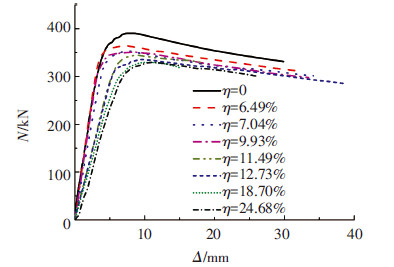
试验得到了不同锈蚀程度压弯试件的荷载N与跨中侧向挠度Δ之间关系曲线,见图 5.在加载初期,各试件的跨中挠度均随着荷载的增加线性增长,当锈蚀率小于10%时,挠度的增长速率基本保持不变,当锈蚀率大于10%时,N-Δ曲线的斜率明显变小,说明腐蚀损伤累计到一定程度后会对试件截面弹性刚度产生较大影响;随着荷载的持续施加,锈蚀试件先于未锈蚀试件进入弹塑性工作阶段,且锈蚀试件达到极限状态时对应的荷载随着锈蚀率的增大不断减小;在承载力下降阶段,A、B两组试件的荷载均随着挠度的增长缓慢下降,说明锈蚀后试件仍然具有一定的延性,但锈蚀试件的挠度增长速率大于未锈蚀试件,证明腐蚀造成了压弯试件失稳后抗弯刚度的急剧衰减.
|
图5 荷载-挠度曲线 |
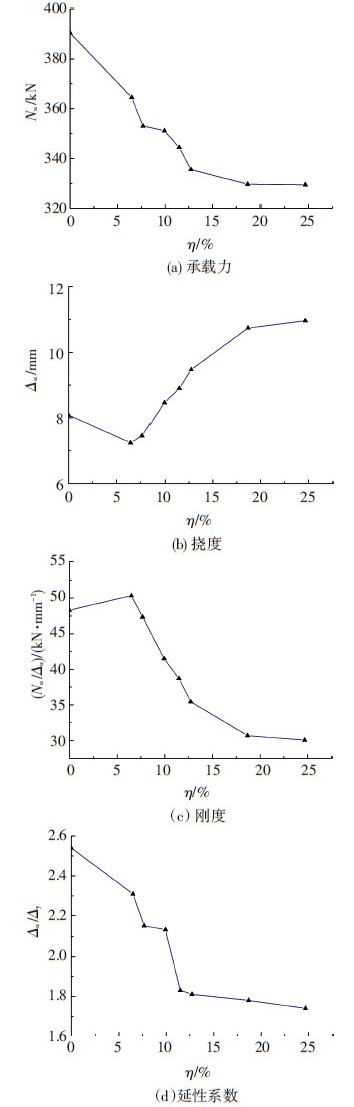
为进一步研究压弯试件整体稳定性能随锈蚀率的退化规律,分别测得各试件的锈蚀率η、屈服挠度Δy、极限荷载Nu及其对应的跨中挠度Δu,列于表 2(其中各试件的锈蚀率根据文献[12]的建议选为受压翼缘锈蚀率).根据表 2内容,分别建立了极限荷载Nu、跨中挠度Δu、刚度Nu/Δu以及延性系数Δu/Δy与锈蚀率η之间的变化趋势图(见图 6),从图 6(a)可发现,腐蚀越严重,压弯试件的材料强度和有效截面积减少越多,试件的极限承载力下降越明显.在图 6(b)、(c)中,腐蚀初期,腐蚀损伤对试件刚度和挠度的影响较小,且由于表 1中锈蚀钢材弹性模量E呈现出一种波动性,这甚至导致锈蚀试件刚度略微增长,挠度变小;但随着腐蚀损伤的累积,锈蚀试件的翼缘和腹板厚度逐渐减小,使得锈蚀试件的截面抗弯刚度明显下降,跨中挠度增大,导致锈蚀试件在相同荷载下的二阶效应加剧,整体稳定性能发生劣化.从图 6(d)可发现随着锈蚀率的增大,锈蚀试件的延性系数逐渐减小,减小程度最大可达32.5%,说明锈蚀试件的塑性变形能力减弱,延性变差.
| 表2 偏心受压试验结果 |
|
图6 承载性能与锈蚀率的关系 |
中国《钢结构设计规范》[13]规定H型截面构件强轴平面内的塑性发展系数为1.05,然而,对于腐蚀环境作用下的压弯构件,其刚度和材料应变硬化性能均随着锈蚀率的增大而减小,这严重制约了压弯构件跨中截面塑性区域的扩展[14, 15],上述塑性发展系数限值是否仍然适用需要进一步研究.
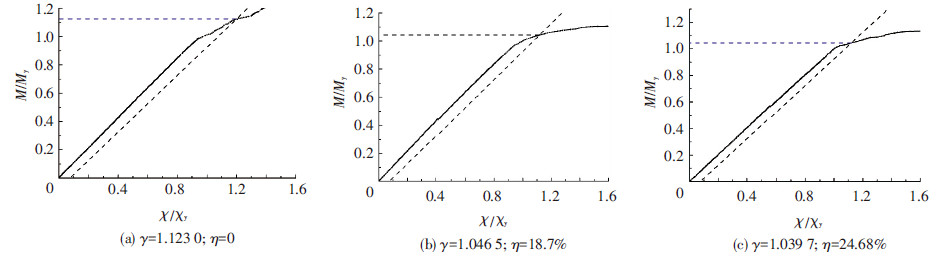
对于构件的塑性发展系数,文献[16]建议可通过截面弯矩-曲率曲线与一条卸载线的交点确定,该卸载线方程为M/My=χ/χy-ε/εy,参考中国和欧洲钢结构设计规范的相关规定,卸载线残余曲率对应的截面最大残余应变为材料屈服应变的7.5%.本文根据上述方法,分别计算不同锈蚀率下压弯试件的塑性发展系数γ,见图 7,χ为跨中截面受压翼缘屈服时对应的屈服曲率,χ=(丨εt丨+丨εp丨)/h,εt、εp分别为跨中截面受拉、受压翼缘应变.塑性发展系数随锈蚀率增大呈逐渐下降趋势,当锈蚀率为18.32%和24.68%时,塑性发展系数仅为1.046 5和1.039 7,说明当腐蚀损伤达到一定程度时,现行规范规定的塑性发展系数限值已不再适用.
|
图7 锈蚀钢柱的塑性发展系数 |
本文采用的锈蚀压弯试件,其截面尺寸和长细比均较单一,为更全面深入研究腐蚀对压弯钢柱承载性能的影响,排除试件尺寸效应和试验误差的干扰,有必要进行有限元数值模拟分析.
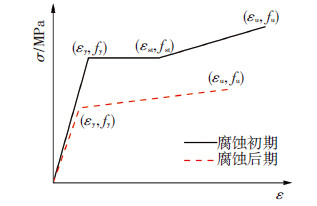
3.1 有限元分析模型及验证采用有限元分析软件ABAQUS进行有限元数值模拟计算.根据文献[17]建议,钢柱采用S4R三维壳单元,端板采用R3D4三维离散刚体壳单元,单元网格尺寸为试件计算长度L的1%,见图 8;有限元模型的截面尺寸和材料性能均考虑腐蚀的影响,其中翼缘和腹板的厚度按照实测锈蚀率进行折减,而锈蚀钢材的应力-应变关系则采用图 9所示本构模型(即随着锈蚀率的增大,屈服平台逐渐消失),具体各应力、应变参数取值根据表 1的材性试验结果和文献[18]的计算方法确定,材料泊松比υ为0.3;对于构件的几何初始缺陷,通过特征值屈曲分析的结果进行施加,即将扰动量级为1/1 000的一阶屈曲模态引入到原始模型中,更新所有单元的节点坐标,再进行非线性屈曲分析.

|
图8 有限元模型的网格划分 |
|
图9 应力-应变关系 |
将采用上述方法计算得到的各试件极限承载力与试验结果进行对比(见图 10),有限元计算结果与试验结果的平均误差仅为1.75%.

|
图10 有限元计算结果与试验结果对比 |
本节利用验证后的有限元数值模拟方法,分别计算不同截面尺寸和长细比的偏心受压钢柱在翼缘锈蚀率为0、10%、20%、30%时的极限承载力和塑性发展系数,共计96个算例.其中,算例共包括8种截面尺寸(见表 3),而每种截面尺寸对应3种长细比(λ=30、55、80);试件的加载方式仍然为单向偏心偏压加载,偏心距为截面形心至受压翼缘中心线间距离;锈蚀模型的翼缘和腹板厚度损失量相同,即按照翼缘原始厚度与锈蚀率的乘积对翼缘、腹板厚度进行折减,见图 11.
| 表3 有限元模拟试件截面尺寸 |

|
图11 翼缘、腹板厚度损失示意 |
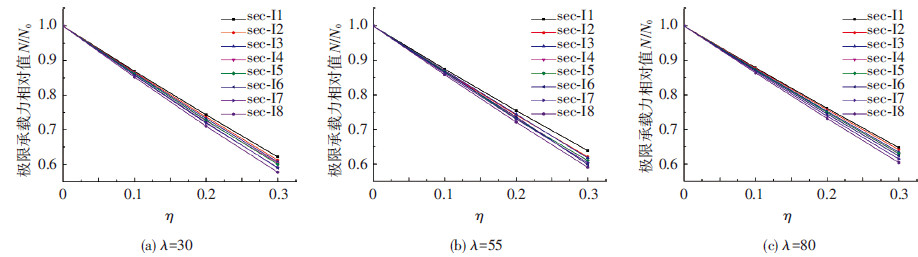
图 12分别给出了3种长细比对应的5种截面尺寸试件的极限承载力相对值与锈蚀率之间的对应关系,通过对相同长细比不同截面尺寸试件的模拟结果进行比较可发现,tf/tw相对较大的试件,其承载力退化的现象更为明显,因为,对于不同截面尺寸的试件,在翼缘板锈蚀率相同的情况下,腹板锈蚀程度随tf/tw的增大而增大,导致tf/tw较大试件的截面面积和力学性能下降幅度更大;通过对相同截面尺寸不同长细比试件的模拟结果进行比较可发现,试件长细比越小,其极限承载力的退化幅度越大,因为,腐蚀使得板件宽厚比增大,导致锈蚀试件在整个受力过程中发生板件局部屈曲,然而,长细比越大的试件,在整体失稳前越不易产生局部屈曲,故其承载力下降的幅度相对较小.
|
图12 不同尺寸试件模拟结果对比 |
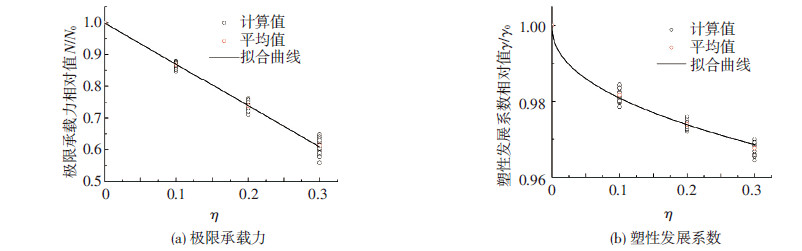
如图 13所示,所有算例的极限承载力相对值随锈蚀率呈线性下降趋势,而塑性发展系数相对值随锈蚀率呈指数下降趋势.试件长细比、tf/tw等参数会对承载性能造成一定影响,但影响程度有限,本文为了提出适用性更为广泛的承载性能退化规律公式,采用η分别对图 13(a)、(b)中数据点平均值进行拟合,具体表示为:
|
图13 承载性能参数退化规律 |
| $N/{{N}_{0}}=1-1.29\eta,$ | (5) |
| $\gamma/{{\gamma }_{0}}=1-0.054{{\eta }^{0.451}}.$ | (6) |
式中:N、N0为锈蚀和未锈蚀试件的整体稳定承载力,γ、γ0分别为锈蚀和未锈蚀试件的塑性发展系数.
4 承载力计算公式中国现行钢结构规范规定,弯矩作用在对称轴平面内的实腹式压弯构件,其平面内稳定性应按下式计算:
| $\frac{N}{\varphi A}+\frac{{{\beta }_{\text{m}}}M}{\gamma W\left(1-0.8N/N{{'}_{E}} \right)}\le f.$ | (7) |
对于锈蚀后的试件,在采用上述公式计算其承载力时,需要考虑截面面积损失、材料强度退化以及塑性发展系数折减三方面因素.为便于试验结果与设计公式的比较,分别选取一定锈蚀率试件的NP-MP理论相关曲线与试验、有限元结果进行对比.其中,在绘制各锈蚀试件的NP-MP理论相关曲线时,设计公式中φ、A、W和N′E均按图 11所示截面削减方法进行重新计算,f、γ则分别根据式(2)、(6)进行调整(各式中锈蚀率均为翼缘锈蚀率).
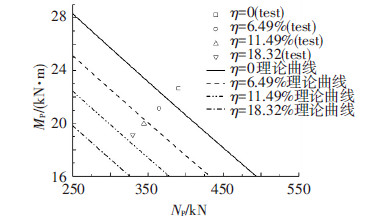
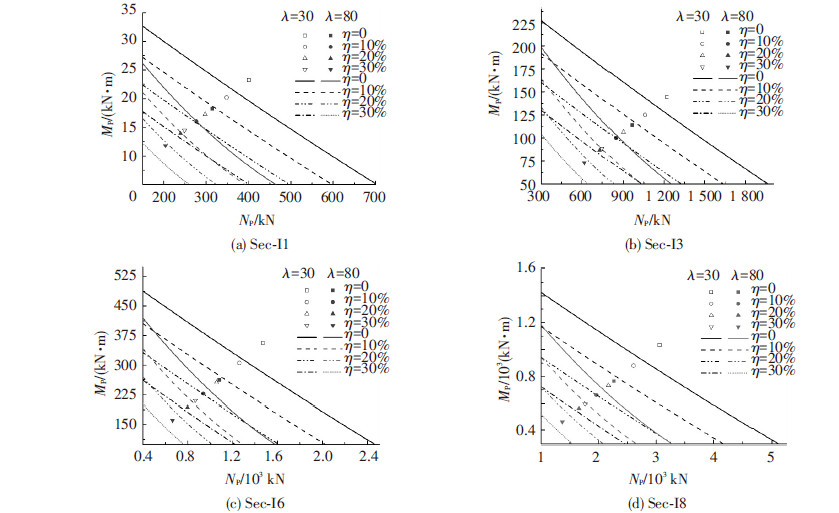
本文列出部分试件的NP-MP理论相关曲线与试验、有限元结果的对比,见图 14、15.所有试验、有限元结果的数据点均位于NP-MP理论曲线的上方,说明对于锈蚀后的压弯构件,在考虑了截面面积损失、材料强度退化以及塑性发展系数折减三方面因素后,采用现行规范式(7)设计方法依然安全可靠.
|
图14 试件Mp-Np理论曲线与试验结果对比 |
|
图15 试件Mp-Np理论曲线与有限元结果对比 |
1)对7根H型钢构件进行了最长达3 a的自然暴露盐雾加速腐蚀试验,并从各锈蚀型钢构件上截取板材试样进行力学性能试验,建立了各项力学性能指标与锈蚀率的关系式.
2)分别对2根未锈蚀H型钢柱和7根氯盐腐蚀H型钢柱进行偏压承载力试验,发现锈蚀试件的破坏形态仍然以整体失稳为主,随着锈蚀率的增加,试件的承载力、抗弯刚度和延性系数下降,挠度增大.
3)腐蚀损伤使得钢材的应变强化效应减弱,塑性变形能力下降,影响锈蚀试件的塑性性能利用,导致截面塑性发展系数随着锈蚀率的增加而减小.
4)对大量的有限元数值计算结果进行分析,发现tf/tw越大、长细比越小,极限承载力下降越明显;通过对模拟计算结果的平均值进行拟合,建立了偏心受压钢柱的整体稳定承载力、塑性发展系数随锈蚀率的退化规律公式.
5)在考虑截面面积损失、材料强度退化以及塑性发展系数折减三方面因素的情况下,采用现行钢结构设计规范进行锈蚀压弯试件的整体稳定性设计依然安全可靠.
| [1] | 邱斌, 徐善华. 锈蚀钢板力学性能的退化规律[J]. 机械工程材料, 2014, 38(10): 60-64.( 1) 1) |
| [2] | PAIK J K, THAYAMBALLI A K. Ultimate strength of ageing ships [J]. Journal of Engineering for the Maritime Environment, 2002, 216(1):57-77.( 1) 1) |
| [3] | 王波, 袁迎曙, 李富民, 等. 氯盐锈蚀钢筋的屈服强度退化分析及其概率模型[J]. 建筑材料学报, 2011, 14(5): 597-603.( 1) 1) |
| [4] | 徐善华, 任松波, 崔焕平, 等. 锈蚀槽钢受弯承载力试验研究[J].实验力学, 2014, 29(4): 506-512.( 1) 1) |
| [5] | 史炜洲, 童乐为, 陈以一, 等. 腐蚀对钢材和钢梁受力性能影响的试验研究[J]. 建筑结构学报, 2012, 33(7):53-60.( 1) 1) |
| [6] | 张春涛, 范文亮, 李正良. 腐蚀环境中Q345等边角钢构件拟静力试验研究[J]. 工程力学, 2014, 31(11): 53-62.( 1) 1) |
| [7] | BEAULIEU L V, LEGERON F, LANGLOIS S. Compression strength of corroded steel angle members [J]. Journal of Constructional Steel Research, 2010, 66: 1366-1373.( 1) 1) |
| [8] | 林翠, 王凤平, 李晓刚. 大气腐蚀研究方法进展[J]. 中国腐蚀与防护学报, 2004, 24(4): 249-256.( 1) 1) |
| [9] | 刘明. 大气腐蚀模拟加速试验及相关性研究[D]. 北京: 北京航空材料研究院, 2003.( 1) 1) |
| [10] | 金属材料拉伸试验第1部分: 室温试验方法:GB/T 228—2010[S]. 北京: 中国标准出版社, 2010.( 1) 1) |
| [11] | 班慧勇, 施刚, 石永久. 960 MPa高强度钢材轴压构件整体稳定性能试验研究[J]. 建筑结构学报, 2014, 35(1): 117-125.( 1) 1) |
| [12] | 于峰, 黎德光, 徐国士, 等, 锈蚀槽钢梁荷载-挠度关系研究[J]. 钢结构, 2013, 28(2): 78-81.( 1) 1) |
| [13] | 钢结构设计规范:GB 50017—2003[S]. 北京: 中国计划出版社, 2003.( 1) 1) |
| [14] | 王飞, 施刚, 戴国欣, 等. 屈强比对钢框架抗震性能影响研究进展[J]. 建筑结构学报, 2010(增刊1):18-22.( 1) 1) |
| [15] | 陈绍蕃. 钢结构设计原理[M]3版. 北京: 科学出版社, 2005.( 1) 1) |
| [16] | 王元清, 高博, 戴国欣, 等. 双轴对称不锈钢受弯构件残余变形的影响因素分析[J]. 山东大学学报(工学版), 2011, 41(1): 95-100.( 1) 1) |
| [17] | 陈娟. 考虑初始缺陷的中厚壁冷弯方矩管柱极限承载力研究[D]. 武汉: 武汉理工大学, 2008.( 1) 1) |
| [18] | 张伟平, 商登峰, 顾祥林. 锈蚀钢筋应力-应变关系研究[J]. 同济大学学报(自然科学版), 2006, 34(5): 586-592.( 1) 1) |
 2016, Vol. 48
2016, Vol. 48


