2.兰州大学 土木工程与力学学院,730000兰州;
3. 结构工程灾变与控制教育部重点实验室(哈尔滨工业大学),150090 哈尔滨
2.School of Civil Engineering and Mechanics, Lanzhou University, 730000 Lanzhou, China;
3.Key Lab of Structures Dynamic Behavior and Control (Harbin Institute of Technology), Ministry of Education, 150090 Harbin, China
桥梁健康监测是热点研究领域,主要经历两个阶段:第一个阶段主要是安装传感器,获得监测数据,大量研究主要集中在数据传送系统、数据压缩系统、数据恢复系统、数据获得技术和系统组装技术等[1, 2, 3, 4, 5, 6],目前已处于成熟阶段[7],当前的健康监测系统不仅能够监测到结构的响应,而且能够连续监测车辆、风、温度、地震、船撞等荷载[8];第二个阶段为健康监测信息的应用,健康监测系统提供了大量监测数据,如何合理地处理监测数据是健康监测领域的主要困难之一,目前大量研究主要集中在模态参数识别、损伤识别、模型修正等领域[9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19].而如何利用监测信息进行结构的可靠性评定及预测已成为结构健康监测的瓶颈问题.
基于桥梁结构的离线监测信息来对可靠性进行评估分析,在国内外已展开大量研究,但是怎样利用实时的健康监测信息对可靠性进行实时动态预测评定,国内外研究很少.
本文基于监测的应力信息建立动态模型,引入混合高斯粒子滤波器,并采用粒子滤波方法、贝叶斯方法和FOSM方法实现了桥梁构件可靠性的实时动态预测分析.
1 基于桥梁监测信息的动态模型桥梁健康监测系统在长期运营中积累了大量健康监测信息,这些监测信息经过五点三次平滑之后可用来构造本文的状态方程.基于桥梁结构长期大量的健康监测数据(应力信息),可统计回归分析得到动态非线性模型.
监测方程:
| ${{y}_{t+1}}={{\theta }_{t+1}}={{v}_{t+1}},{{v}_{t+1}}\tilde{\ }N\left[ 0,V \right],$ | (1) |
状态方程:
| ${{\theta }_{t+1}}=f\left( {{\theta }_{t}} \right)+{{\omega }_{t}},{{\omega }_{t}}\tilde{\ }N\left[ 0,W \right],$ | (2) |
初始状态信息:
| $\left. {{\theta }_{t}} \right|{{D}_{t}}\tilde{\ }p\left( \left. {{\theta }_{t}} \right|{{D}_{t}} \right).$ | (3) |
式中:yt为t时刻的监测值;νt+1为观测白噪声;V为监测误差的方差,通过监测数据与平滑处理之后的数据信息来近似估计;θt为状态变量;ft(·)为状态转移函数,它可通过监测数据的低频趋势项随机信息来近似得到;ωt为状态白噪声;W为状态误差的方差,由平滑处理之后的数据近似估计;p(θt|Dt)是初始状态变量的概率分布,它主要基于已有大量的健康监测信息,通过平滑处理得到新的低频随机样本,然后对新样本进行概率统计得到.
基于动态模型(式(1)~(3)),通过概率预测和更新递推估计出概率预测模型.
系统状态θt+1的先验概率分布p(θt+1|Dt):
| $p\left( \left. {{\theta }_{t+1}} \right|{{D}_{t}} \right)=\int{p\left( \left. {{\theta }_{t+1}} \right|{{D}_{t}} \right)p\left( \left. {{\theta }_{t}} \right|{{D}_{t}} \right)\text{d}}{{\theta }_{t}},$ | (4) |
监测值的一步向前预测分布p(yt+1|Dt):
| $p\left( \left. {{y}_{t+1}} \right|{{D}_{t}} \right)=\int{p\left( \left. {{\theta }_{t+1}} \right|{{D}_{t}} \right)p\left( \left. {{y}_{t+1}} \right|{{\theta }_{t+1}} \right)\text{d}}{{\theta }_{t+1}},$ | (5) |
系统状态θt+1的后验概率分布p(θt+1|Dt+1):
| $p\left( \left. {{\theta }_{t+1}} \right|{{D}_{t+1}} \right)=\frac{p\left( \left. {{\theta }_{t+1}} \right|{{D}_{t}} \right)p\left( \left. {{y}_{t+1}} \right|{{\theta }_{t+1}} \right)}{p\left( \left. {{y}_{t+1}} \right|{{D}_{t}} \right)}.$ | (6) |
基于监测信息的滤波器系统状态θt+1的先验概率分布可对其采用高斯分布来混合近似.根据式(1)、(2),假定p(θt|Dt)可由高斯分布混合近似,即
| $p\left( \left. {{\theta }_{t}} \right|{{D}_{t}} \right)\approx \sum\limits_{i=1}^{{{n}_{1}}}{{{p}_{t,i}}N\left[ {{\theta }_{t}},{{\mu }_{t,i}},\sigma _{t,i}^{2} \right]}.$ | (7) |
结合状态方程,式(4)可由混合高斯分布模型来近似模拟,即
| $p\left( \left. {{\theta }_{t+1}} \right|{{D}_{t}} \right)\approx \sum\limits_{i=1}^{{{n}_{2}}}{{{\overline{p}}_{t+1,i}}N\left[ {{\theta }_{t+1}},{{\overline{\mu }}_{t+1,i}},\overline{\sigma }_{t+1,i}^{2} \right]}.$ | (8) |
式中:$\sum\limits_{i=1}^{{{n}_{1}}}{{{p}_{t}}}=\sum\limits_{i=1}^{{{n}_{2}}}{{{\overline{p}}_{t+1,i}}=1}$,且pt,i,Pt+1,i≥0,N[·]表示正态概率分布函数.由文献[20]可知,n1=n2,它们都表示高斯混合模型中混合成分的数量.
2.1 基于监测信息的状态θt+1后验分布得到新的监测值yt+1之后,基于式(6)可得到状态θt+1的后验概率分布为
| $\begin{align} & p\left( \left. {{\theta }_{t+1}} \right|{{D}_{t+1}} \right)={{C}_{t+1}}p\left( \left. {{\theta }_{t+1}} \right|{{D}_{t}} \right)p\left( \left. {{y}_{t+1}} \right|{{\theta }_{t+1}} \right)\approx \\ & {{C}_{t+1}}p\left( \left. {{y}_{t+1}} \right|{{\theta }_{t+1}} \right)\sum\limits_{i=1}^{{{n}_{2}}}{{{\overline{p}}_{t+1,i}}N\left[ {{\theta }_{t+1}},{{\overline{\mu }}_{t+1,i}},\overline{\sigma }_{t+1,i}^{2} \right]}. \\ \end{align}$ | (9) |
混合高斯粒子滤波器测量更新是通过高斯分布近似上述滤波概率分布,即$\hat{p}\left(\left.{{\theta }_{t+1}} \right|{{D}_{t+1}} \right)=\sum\limits_{i=1}^{n}{{{p}_{i}}}N\left[{{\theta }_{t+1}},{{\mu }_{t+1}},i,{{\sigma }^{2}}_{t+1,i} \right]$.根据监测方程可知p(yt+1|θt+1)为正态方程,一般情况下p(θt+1|Dt+1)的均值和方差不能精确求解.针对高斯粒子滤波则是通过对重要性函数q(θt+1|Dt+1)=p(θ
| ${{\mu }_{i+1}}=\sum\limits_{i=1}^{M}{\frac{1}{M}\hat{\theta }_{t+1}^{\left( i \right)}},$ | (10) |
| $\sum{_{t+1}}=\sum\limits_{i=1}^{M}{\frac{1}{M}}{{\left( {{\overline{\mu }}_{t+1}}-\hat{\theta }_{t+1}^{\left( i \right)} \right)}^{2}}.$ | (11) |
式中:M表示样本总数,μt+1为状态θt+1的后验概率分布平均值,Σt+1为状态θt+1的后验概率分布方差.
基于重抽样的样本$\hat{\theta }_{t+1}^{\left(i \right)}$,可得更新后状态θt+1的后验概率分布近似为
| $p\left( \left. {{\theta }_{t+1}} \right|{{D}_{t+1}} \right)\approx \sum\limits_{i=1}^{{{n}_{1}}}{{{p}_{t+1}}_{,i}}N\left[ {{\theta }_{t+1}},{{\mu }_{t+1,i}},\sigma _{t+1,i}^{2} \right].$ | (12) |
混合高斯粒子滤波器可将2.1节的滤波分布近似为正态分布.基于t+1时刻状态θt+1的滤波分布p(θt+1|Dt+1),结合状态方程,进一步可得到预测分布,即状态θt+2的先验概率分布p(θt+2|Dt+1)为
| $p\left( \left. {{\theta }_{t+2}} \right|{{D}_{t+1}} \right)=\int{p\left( \left. {{\theta }_{t+2}} \right|{{\theta }_{t+1}} \right)p\left( \left. {{\theta }_{t+1}} \right|{{D}_{t+1}} \right)\text{d}}{{\theta }_{t+1}}.$ | (13) |
式(13)可近似为
| $\begin{align} & p\left( \left. {{\theta }_{t+2}} \right|{{D}_{t+1}} \right)= \\ & \ \ \ \ \ \int{p\left( \left. {{\theta }_{t+2}} \right|{{\theta }_{t+1}} \right)\sum\limits_{i=1}^{{{n}_{1}}}{{{p}_{t+1}}_{,i}}N\left[ {{\theta }_{t+1}},{{\mu }_{t+1,i}},\sigma _{t+1,i}^{2} \right]}\text{d}{{\theta }_{t+1}}. \\ \end{align}$ | (14) |
利用2.1节中得到的粒子$\hat{\theta }_{t+1}^{\left(i \right)}$以及权重wt+1(i)可近似得到预测分布函数为
| $p\left( \left. {{\theta }_{t+2}} \right|{{D}_{t+1}} \right)\approx \frac{1}{M}\sum\limits_{i=1}^{M}{w_{t+1}^{\left( i \right)}p\left( \left. {{\theta }_{t+2}} \right|\hat{\theta }_{t+1}^{\left( i \right)} \right)},$ | (15) |
| $\ p\left( \left. {{\theta }_{t+2}} \right|\hat{\theta }_{t+1}^{\left( i \right)} \right)=N\left[ {{\theta }_{t+2}},f\left( \hat{\theta }_{t+1}^{\left( i \right)} \right),W \right].$ | (16) |
依次从状态转移分布$p\left(\left.\theta _{t+2}^{\left(i \right)} \right|\hat{\theta }_{t+1}^{\left(i \right)} \right)$,i=1,2,...M抽样得到t+2时刻的状态粒子θt+2(i),i=1,2,...M,从而可得预测概率分布的分布参数:
| ${{\mu }_{t+2}}=\frac{1}{M}\sum\limits_{i=1}^{M}{w_{t+1}^{\left( i \right)}}\theta _{t+2}^{\left( i \right)},$ | (17) |
| $\sum{_{t+2}}=\frac{1}{M}{{\sum\limits_{i=1}^{M}{w_{t+1}^{\left( i \right)}\left( \left. {{\mu }_{t+2}} \right|\theta _{t+2}^{\left( i \right)} \right)}}^{2}}.$ | (18) |
式中μt+2为平均值,Σt+2为方差.
2.3 监测变量yt+2的一步向前预测分布基于状态θt+2的先验概率分布p(θt+2|Dt+1),参考式(5)和式(15),利用2.2节得到的粒子θt+2(i)以及权重wt+1(i),可近似得到yt+2的一步向前预测分布p(yt+2|Dt+1)为:
| $p\left( \left. {{y}_{t+2}} \right|{{D}_{t+1}} \right)=\frac{1}{M}\sum\limits_{i=1}^{M}{w_{t+1}^{\left( i \right)}}p\left( \left. {{y}_{t+2}} \right|\theta _{t+2}^{\left( i \right)} \right),$ | (19) |
| $p\left( \left. {{y}_{t+2}} \right|\theta _{t+2}^{\left( i \right)} \right)=N\left[ {{y}_{t+2}},\theta _{t+2}^{\left( i \right)},V \right].$ | (20) |
依次从转移分布p(yt+2|θt+2(i)),i=1,2,...,M抽样得到t+2时刻的一步向前预测粒子yt+2(i),i=1,2,...M,从而可得一步向前预测分布的分布参数:
| ${{\mu }_{y,t+2}}=\frac{1}{M}\sum\limits_{i=1}^{M}{w_{t+1}^{\left( i \right)}}y_{t+2}^{\left( i \right)},$ | (21) |
| $\sum{y,t+2}=\frac{1}{M}\sum\limits_{i=1}^{M}{w_{t+1}^{\left( i \right)}}{{\left( {{\mu }_{t+2}}-y_{t+2}^{\left( i \right)} \right)}^{2}}.$ | (22) |
式中:μy,t+2为一步向前预测监测值的平均值,Σy,t+2为一步向前预测监测值的方差.
3 混合高斯粒子滤波器的模拟递推基于第2节混合高斯粒子滤波及预测的详细内容,可得混合高斯粒子滤波器的概率模拟递推过程:包括滤波分布参数的概率递推过程、状态预测分布参数的概率递推过程以及一步向前预测监测值分布参数的概率递推过程.
3.1 滤波分布参数的递推过程1)对重要性函数q(θt+1|Dt+1)=p(θt+1|Dt)进行抽样得到样本集(θt+1(i))i=1M;
2)计算各个粒子的权重
| $\overline{w}_{t+1}^{\left( i \right)}=\frac{p\left( \left. {{y}_{t+1}} \right|\theta _{t+1}^{\left( i \right)} \right)p\left( \left. \theta _{t+1}^{\left( i \right)} \right|{{D}_{t}} \right)}{q\left( \left. \theta _{t+1}^{\left( i \right)} \right|{{D}_{t+1}} \right)},$ | (23) |
| $p\left( \left. {{y}_{t+1}} \right|\theta _{t+1}^{\left( i \right)} \right)=N\left[ {{y}_{t+1}},\theta _{t+1}^{\left( i \right)},V \right].$ | (24) |
3)权重标准化
| $w_{t+1}^{\left( i \right)}=\frac{\overline{w}_{t+1}^{\left( i \right)}}{\sum\limits_{i=1}^{M}{\overline{w}_{t+1}^{\left( i \right)}}}.$ | (25) |
基于样本θt+1(i)和权重wt+1(i)的近似离散分布函数,采用重采样方法,即令概率$pr\left(\left.\hat{\theta }_{t+1}^{\left(i \right)} \right|\theta _{t+1}^{\left(i \right)} \right)=w_{t+1}^{\left(i \right)}$,取得样本$\hat{\theta }_{t+1}^{\left(i \right)}$,i表示样本数.
最后按式(10)、(11)计算滤波分布的平均值与方差.
3.2 状态预测分布参数的递推过程1)对概率分布p(θt+1|Dt+1)进行抽样得到粒子$\hat{\theta }_{t+1}^{\left(i \right)}$及其权重wt+1(i);
2)分别对状态转移分布$p\left(\left.\theta _{t+2}^{\left(i \right)} \right|\hat{\theta }_{t+1}^{\left(i \right)} \right)$,i=1,2,...M抽样得到t+2时刻的状态粒子θt+2(i),i=1,2,...M;
3)通过式(17)、(18),可得预测分布的平均值与方差.
3.3 一步向前预测监测值分布参数的递推过程1)对状态转移分布p(θt+2|θt+1),i=1,2,...M,进行抽样得到粒子θt+2(i)及其权重wt+1(i);
2)分别对监测变量转移分布p(yt+2|θt+2(i)),i=1,2,...M抽样得到t+2时刻的监测模拟粒子yt+2(i),i=1,2,...M;
3)通过式(21)、(22),可得预测监测值分布的平均值与方差.
4 桥梁构件可靠性分析及预测基于天津富民桥(悬索桥)吊索的应力监测数据对吊索的可靠性进行在线实时预测.吊索钢丝的抗拉强度按照σ=1 670 MPa来进行分析,主要对吊索考虑了截面强度失效模式,采用的功能函数为
| $g\left( \sigma _{m}^{t} \right)=\sigma -\sigma _{m}^{t},$ | (26) |
式中σtm为t时刻吊索钢丝应力的实时监测值,而且随机变量之间相互独立.
选用吊索钢丝强度的平均值为μσ=1 670 MPa,变异系数为δ=0.15.进一步利用FOSM方法可得吊索考虑不确定性的时变可靠指标预测公式为
| ${{\beta }_{t}}=\frac{{{\mu }_{\sigma }}-\mu \sigma _{m}^{t}}{\sqrt{{{V}_{\sigma }}+V\sigma _{m}^{t}}}.$ | (27) |
式中:μσ和Vσ分别为吊索钢丝强度的平均值和方差,且μσ=σa,Vσ=σa2δ2;μσtm和Vσtm分别为t时刻吊索钢丝应力基于混合高斯粒子滤波器的一步预测平均值和一步预测方差值.
确定性(一步预测方差值为0)的时变可靠指标预测公式为
| ${{\beta }_{t}}=\frac{{{\mu }_{\sigma }}-{{\sigma }_{t}}}{\sqrt{{{V}_{\sigma }}}},$ | (28) |
式中σt为t时刻的应力监测值.
5 算例分析天津富民桥主桥设计为单塔空间索面悬索桥.结合此悬索桥1-2#吊索应力的实时监测信息,对1-2#吊索的可靠性进行实时预测分析.全桥传感器布置见图 1.
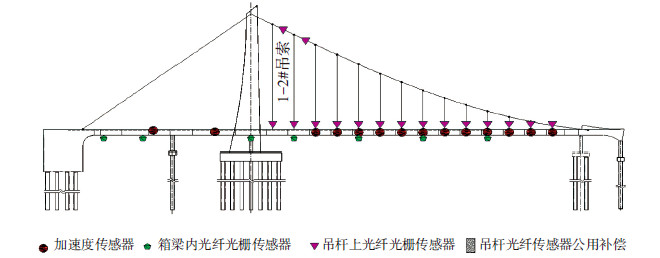
|
图1 天津富民桥传感器布置 |
1-2#吊索安装了3个传感器:FBG01085、FBG01086、FBG01087.从2009年3月23日到2012年9月26日对1-2#吊索应力进行实时监测,期间3个传感器961 d采集到的监测平均值信息见图 2.
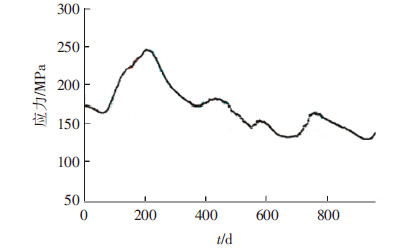
|
图2 监测应力平均值信息 |
对于1-2#吊索来说,采用吊索的平均监测应力信息来进行分析,吊索的平均监测应力信息采用五点三次平滑法平滑处理之后,建立动态方程.
观测方程:
| $\begin{align} & {{y}_{t+1}}={{\theta }_{t+1}}+{{v}_{t+1}}, \\ & {{v}_{t+1}}\tilde{\ }N\left[ 0,V \right]. \\ \end{align}$ | (29) |
状态方程:
| $\begin{align} & {{\theta }_{t+1}}={{\theta }_{t}}+\beta +{{\omega }_{t}}, \\ & \ \ \ \ {{\omega }_{t}}\tilde{\ }N\left[ 0,W \right]. \\ \end{align}$ | (30) |
初始信息:
| $\left. {{\theta }_{t}} \right|{{D}_{t}}\tilde{\ }p\left( \left. {{\theta }_{t}} \right|{{D}_{t}} \right).$ | (31) |
式中β为961d平滑处理的监测应力一阶差分的中位值,近似表示平均监测应力状态的变化趋势.
961 d的平均监测应力信息经五点三次平滑处理之后,对平滑处理的随机应力信息进行概率拟合,可将初始信息的概率分布(式(31))转化为式(32),同时基于平滑处理的应力样本可估计出混合高斯粒子滤波器状态噪声的方差W为20.4 MPa2.基于平滑处理之前与平滑处理之后的应力信息可估计出观测噪声的方差V为998.5 MPa2.模拟长度为1 240;粒子数目为961.本章采取的961个粒子是从初始信息的概率密度函数中采用蒙特卡洛抽样方法得到.为便于表示,假定961个粒子分别表示961 d的粒子.模拟长度1 240表示基于961 d的粒子,并结合后1 240 d实时监测的应力数据,采用混合高斯粒子滤波器来对后1 240 d的应力信息进行实时修正预测.
1-2#吊索961 d监测到的平均监测应力,经平滑处理拟合得到的概率分布见图 3,可看出概率密度函数含有3个峰值,且此分布可通过加权正态分布来拟合,近似拟合的累计概率密度函数可表示为
| $F\left( {{\theta }_{t}} \right)=\sum\limits_{i=1}^{3}{{{p}_{t,i}}}N\left[ {{\theta }_{t}},{{\mu }_{t,i}},\sigma _{^{t,i}}^{2} \right].$ | (32) |
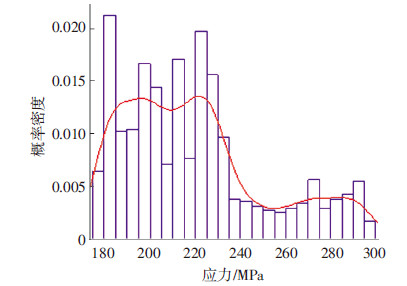
|
图3 拟合1-2#吊索平滑处理应力的分布 |
式中:pt,1+pt,2+pt,3=1,且pt,1>0、pt,2>0、pt,3>0,分别表示不同的应力成分在总应力中所占的比重;N·表示正态分布的累计概率密度函数.且通过最小二乘法或极大似然估计可以确定F(θt)中的各个参数,列于表 1.
| 表1 分布参数拟合结果 |
基于抽取的961个粒子和后1 240 d的实时监测数据,并结合混合高斯粒子滤波器的动态方程,可实现后1 240 d状态值的实时预测和更新,而且能实现监测值的实时动态一步预测.
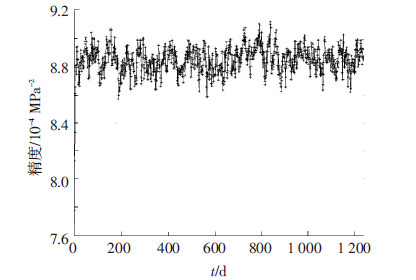
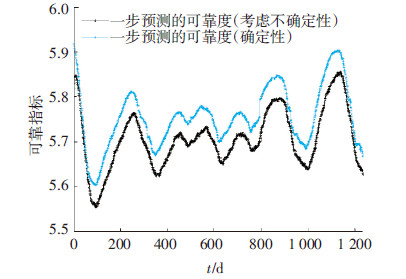
本算例基于1-2#吊索961 d监测得到的应力平均值信息,经过五点三次平滑处理之后,建立了混合高斯粒子滤波器和动态模型来对后1 240 d的应力信息以及可靠性进行预测分析.从图 4可知道,基于混合高斯粒子滤波器得到的应力预测值与监测值变化趋势基本一致,两个曲线几乎重合,而且由图 5可知预测精度基本保持一致,验证了本算例所建高斯粒子滤波器以及动态模型的有效性,并结合式(27)和式(28)对吊索的可靠指标(确定性与不确定性)进行了实时动态预测分析,见图 6,可看出相对于预测得到的确定性可靠指标而言,考虑信息不确定性和随机性预测得到的可靠指标偏小,但它可更合理地评估结构的可靠性.
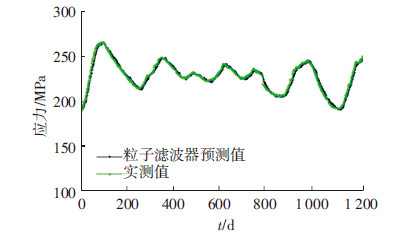
|
图4 基于MGPF的预测值与监测值 |
|
图5 混合高斯粒子滤波器的一步预测精度 |
|
图6 确定性的可靠指标V.S.考虑不确定性的可靠指标 |
利用混合高斯粒子滤波器、桥梁的实时监测信息以及五点三次平滑法来对桥梁构件的可靠性进行实时在线预测分析.从预测结果来看,模拟预测值与实测值变化趋势基本一致,预测精度基本平稳.而且从图 4可知,混合高斯粒子滤波器初始状态信息的模拟粒子越详细,则预测得到的应力信息精度越好,最后基于实时监测和预测的应力参数对构件的可靠性进行了实时预测,由于混合高斯粒子滤波器预测考虑了监测信息的随机性,因而预测的可靠性比确定性的可靠性偏小,但更符合工程实际情况.本文作者将基于桥梁体系的大量健康监测信息,采用混合高斯粒子滤波器,对模拟粒子数目与预测精度之间的关系和桥梁体系的可靠性实时预测展开详细研究.
| [1] | 李惠, 周文松, 欧进萍,等. 大型桥梁结构智能健康监测系统集成技术研究[J]. 土木工程学报, 2006, 39(2): 46-52.( 1) 1) |
| [2] | 李爱群, 缪长青, 李兆霞, 等. 润扬长江大桥结构健康监测系统研究[J]. 东南大学学报, 2003, 33(5): 544-548.( 1) 1) |
| [3] | 秦权. 桥梁结构的健康监测[J]. 中国公路学报, 2000, 13(2): 37-42.( 1) 1) |
| [4] | CHANA T H T, YUA L, TMA H Y. Fiber bragg grating sensors for structural health monitoring of Tsing Ma Bridge: background and experimental observation [J]. Engineering Structures, 2006, 28: 648-659.( 1) 1) |
| [5] | HODGSON I. Personal discussion for the acquisition of the real data from the monitoring of the I-39 Northbound Bridge over the Wisconsin River[R]. Bethlehem, Pennsylvania: Lehigh University, Department of Civil and Environmental Engineering,2007: 18015-4729.( 1) 1) |
| [6] | HU XY, WANG B, JI H. A Wireless sensor network-based structural health monitoring system for highway bridges [J]. Computer-Aided Civil and Infrastructure Engineering, 2013, 28(3): 193-209.( 1) 1) |
| [7] | LIU M, FRANGOPOL D M, KIM S. Bridge safety evaluation based on monitored live load effects[J]. Journal of Bridge Engineering, 2009, 14(4): 257-269.( 1) 1) |
| [8] | 王瑀, 荆国强, 王波. 桥梁健康监测系统在线结构分析及状态评估方法[J]. 桥梁建设, 2014, 44(1): 25-30.( 1) 1) |
| [9] | CHING J, MUTO M, BECK J L. Structural model updating and health monitoring with incomplete modal data using gibbs sampler [J]. Computer-Aided Civil and Infrastructure Engineering, 2006, 21(4): 242-257.( 1) 1) |
| [10] | GARCIA-PALENCIA A J, SANTINI-BEL L. A two-step model updating algorithm for parameter identification of linear elastic damped structures [J]. Computer-Aided Civil and Infrastructure Engineering, 2013, 28(7): 509-521.( 1) 1) |
| [11] | 李顺龙.基于健康监测技术的桥梁结构状态评估和预警方法研究[D]. 哈尔滨:哈尔滨工业大学, 2009.( 1) 1) |
| [12] | LOZANO-GALANT J A, NOGAL M, CASTILLO E, et al. Application of observability techniques to structural-system identification [J]. Computer-Aided Civil and Infrastructure Engineering, 2013, 28(6): 343-450.( 1) 1) |
| [13] | OSORNIO-RIOS R A. MUSIC-neural network analysis for locating structural damage in truss-type structures by means of vibrations[J]. Computer-Aided Civil and Infrastructure Engineering, 2012, 27(9): 687-698.( 1) 1) |
| [14] | O’BYME M. Texture analysis based damage detection of ageing infrastructural elements[J]. Computer-Aided Civil and Infrastructure Engineering, 2013, 28(3): 162-177.( 1) 1) |
| [15] | QIAO L. Signal pattern-recognition for damage diagnosis in structures [J]. Computer-Aided Civil and Infrastructure Engineering, 2012, 27(9): 699-710.( 1) 1) |
| [16] | TORBOL M, GOMEZ H, FENG M. Fragility analysis of highway bridges based on long term monitoring data [J]. Computer-Aided Civil and Infrastructure Engineering, 2013, 28(3): 178-192.( 1) 1) |
| [17] | WALSH S B. Data processing of point clouds for object detection for structural engineering applications [J]. Computer-Aided Civil and Infrastructure Engineering, 2013, 28(7): 495-508.( 1) 1) |
| [18] | XANGI J, LIANG M. Wavelet-based detection of beam cracks using modal shape and frequency measurements [J]. Computer-Aided Civil and Infrastructure Engineering, 2012, 27(6): 439-454.( 1) 1) |
| [19] | YUEN K V, KATAFYGIOTIS L S. Substructure identification and health monitoring using response measurement only [J]. Computer-Aided Civil and Infrastructure Engineering, 2006, 21(4): 280-291.( 1) 1) |
| [20] | 彭云辉, 刘云峰, 缪栋, 等. 高斯混合粒子滤波器在状态估计中的应用[J]. 弹箭与制导学报,2007,27(1): 271-274.( 1) 1) |
 2016, Vol. 48
2016, Vol. 48


