2.首都世界城市顺畅交通北京市协同创新中心,100124 北京
2.Beijing Collaborative Innovation Center for Metropolitan Transportation, 100124 Beijing, China
结构抗震设计理论的发展经历了静力理论、反应谱理论、动力时程分析和基于性能的设计理论4个阶段.对于一般性结构,目前大多数国家仍将抗震设计反应谱作为估计结构在使用年限内可能遭受的地震作用水平的主要依据和手段.
地震反应谱是指单质点体系在给定阻尼及地震动作用下的最大反应随其自振周期变化的曲线.抗震设计反应谱是以地震反应谱特性为依据,在获取大量地震动的反应谱基础之上加以统计分析和平滑处理并结合经验判定确定的曲线.由于地震动是典型的时频非平稳随机振动,影响地震动反应谱的因素丰富且复杂,获得适用性强的抗震加速度设计谱十分困难.目前各国或地区基本上均采用分段函数的形式并通过反应谱平台值(中国规范采用地震影响系数最大值) 和特征周期2个特征参数来表征反应谱的基本形状,但这些抗震设计反应谱在形状及周期控制点等方面不仅存在明显差异,而且存在大量的不确定性.各国或地区抗震设计反应谱的不同导致了其抗震设计水平及结构的抗震性能也存在较大差异性,消除这种差异有利于结构抗震设计水平的提高.
此外,抗震设计规范中的反应谱一般都是指某种标准化的绝对加速度谱,并没有直接给出相对速度谱和相对位移谱.实际上,对于复杂地震动或长周期结构,地震动的速度和位移时程对结构的动力反应也具有显著的作用,如果直接利用与实际谱特征有较大差异的加速度设计反应谱并简单地根据拟谱关系确定相对速度谱和相对位移谱等低阶谱,将进一步放大这种误差.因此,不能保证仅通过绝对加速度谱生成的人工地震波在频谱特性等方面与实际地震动的统计特性完全相似,在某些情况这些误差可能会严重影响结构抗震减震的分析结果和设计水平.
综上所述,针对抗震设计反应谱目前的研究不足,提出新型的反应谱函数形式从而提高其适用性,并确保其低阶谱的频谱特征能够与相应的真实谱值接近,进而能够合成更精确的人工地震波是十分必要的.本文提出了统一光滑反应谱的概念,并对其精度、简便性和适用性进行了对比及验证,最后提出了基于光滑反应谱并考虑低阶谱的人工地震动合成方法.
1 关于设计反应谱谱形的讨论1934年Biot[1]提出了地震动反应谱的基本理论,其反应谱形式为具有明显尖端点的连续曲线.20世纪40年代Housner[2]对多条地震动反应谱进行规准化再取平均获得了用连续型曲线形式表示的抗震设计谱,此后反应谱理论逐渐得到推广和应用.20世纪60年代末,Newmark等[3]认为反应谱的高频、中频和低频段分别与地震动的加速度、速度和位移幅值相关,设计谱应该用规准谱分别乘以相应的地震动幅值用直线段来表示,进而提出了三联坐标系下直线分段式设计谱模型.Newmark提出的设计谱带有明显的经验化特征,首先设计谱的形状与几个固定周期有关,其次各区段谱值与地震动幅值均成固定比例.尽管分段式设计谱模型的精细度略差,但其仍以众多优点被研究者普遍接受并在绝大部分国家或地区的抗震设计规范中加以沿用和推广,而有关连续光滑型反应谱的研究日渐式微.
目前,绝大部分国家或地区抗震设计规范中的设计谱采用的是自然坐标下的分段表达形式[4, 5, 6, 7].设计谱的加速度控制段一般由上升斜直线段和平台段组成;速度控制段主要由指数衰减曲线表达,也有用斜直线下降段表达的情况;位移控制段的表达主要有指数衰减曲线、平台段或斜直线下降段几种形式.广义设计谱由斜直线上升段、平台段和指数衰减曲线段组成,可表示为
| ${{s}_{a}}\left( T \right)=\left\{ \begin{align} & {{\alpha }_{m}}+{{\alpha }_{m}}\left( {{\beta }_{m}}-1 \right)\left( T/{{T}_{0}} \right),0< T\le {{T}_{0}}; \\ & {{\alpha }_{m}}{{\beta }_{m}},\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{T}_{0}}< T\le {{T}_{g}}; \\ & {{\alpha }_{m}}{{\beta }_{m}}{{\left( {{T}_{g}}/T \right)}^{\gamma }},\ \ \ \ \ \ \ \ \ \ \ \ \ {{T}_{g}}< T\le {{T}_{W}};\ \\ & {{\alpha }_{m}}{{\beta }_{m}}{{\left( {{T}_{g}}/T \right)}^{\gamma }}{{\left( {{T}_{g}}/T \right)}^{v}},\ \ \ \ \ \ \ \ {{T}_{W}}< T. \\ \end{align} \right. $$ | (1) |
式中:αm为地震动加速度峰值,βm为规准设计谱平台幅值或反应最大放大倍数,T0、Tg、Tw分别表示第一拐点周期、第二拐点周期(特征周期)和第三拐点周期,γ为曲线下降一段的衰减指数,ν为曲线下降二段的调整指数.各国抗震设计规范中相应参数取值各有不同[8, 9],美国规范NEHRP2003和欧洲规范Eurocode8均采用了上式形式,且ν为1.日本抗震设计规范中谱曲线的下降一段和二段是光滑连续的,即ν为0.中国抗震设计规范反应谱前三段符合上式,但下降二段采用了直线形式.
分段式设计谱的各段函数虽然相对准确地体现了结构在不同频域内的频谱特性,但是各段函数的连接处是连续但不光滑的,这些局限导致分段式设计谱存在以下严重不足:(1) 不同频段的分段式设计谱具有不同的统计特征及离散性;(2) 分段式设计谱在不同周期拐点处的谱值与统计结果偏差较大;(3) 分段式设计谱的形状不能与反应谱的整体变化特征完全吻合;(4) 高阶分段式设计谱的谱形略有偏差就可能导致低阶谱形严重偏离实际特征.因此在对传统的分段式设计谱的特性继续进行深入研究的基础上,有必要追根溯源,通过详细比较和分析不同国家或地区规范设计反应谱不足和局限,对抗震设计谱的最优谱形及基本模式进行探讨和改进[10].
从自然界发生的现象及其普遍规律来看,各种物理量的变化往往是连续的,由此衍化的参数或性能表征在数学形式上也应该是光滑函数而不是简单生硬的多拐点函数.众多研究成果表明,对大量地震动数据进行计算得到的加速度反应谱的均值曲线是典型的光滑曲线,并没有明显的平台和拐点.因此,在充分考虑大量地震动的统计特征及变化规律的基础上,提出具有普适性的统一光滑设计谱对地震动及抗震设计反应谱研究均有重大的理论意义及应用价值.
事实上,对光滑反应谱的研究虽然少见,但仍然长期存在.胡聿贤[11]曾对32个国家或地区的40个加速度设计谱进行了统计,结果表明只有智利于1972年颁布的抗震设计规范曾采用光滑反应谱,其函数形式为
| ${{s}_{\text{a}}}=0.2{{\alpha }_{m}}T{{T}_{g}}/\left( T_{g}^{2}+{{T}^{2}} \right).$ | (2) |
由上式确定的反应谱在中长周期段与实际地震动的均值谱差异较大,适用性差.1996年智利在抗震规范NCh433[12]中规定的抗震设计反应谱计算公式为
| ${{s}_{\text{a}}}=\frac{I{{\alpha }_{m}}}{{{R}^{*}}}\frac{1+4.5{{\left( {{T}_{n}}/{{T}_{g}} \right)}^{p}}}{{{\left( {{T}_{n}}/{{T}_{g}} \right)}^{3}}},$ | (3) |
式中:I为与结构相关的系数,R*为与结构周期相关的衰减因子,Tn为结构第n阶振型对应的周期,对于Ⅰ类和Ⅱ类场地,p分别取2.0和1.5,对于Ⅲ类和Ⅳ类场地,p均取1.0.上述的反应谱谱形虽然是光滑的,但其形式复杂,应用不便,更重要的是由其变换得到的低阶谱误差仍然较大.上述缺陷限制了对该谱的肯定及推广.
2001年美国AEC颁布了新的核电指导标准NUREG/CR 6728[13].NUREG设计谱的确定以大量强震记录为基础,参考了岩石场地概率地震危险性分析结果,并采用了曲线函数表达为
| $ln\left[ {{s}_{\text{a}}}\left( f \right)/{{\alpha }_{m}} \right]=\frac{{{c}_{1}}}{\cosh \left( {{c}_{2}}{{f}^{{{c}_{3}}}} \right)}+{{c}_{4}}\left[ \frac{\exp \left( {{c}_{5}}f \right)}{{{f}^{{{c}_{6}}}}} \right],$ | (4) |
式中:f为结构频率,αm为地震动加速度峰值,c1~c5为与震级和震中距有关的参数.NUREG设计谱的特点是其谱形考虑了地震危险性分析的结果,且与地震动平均反应谱的变化趋势相近.但该谱在函数形式上与传统的抗震设计谱差异较大,参数较多,且采用了对数坐标,转换到自然坐标后数值浮动较大,尚不能直接在普通结构抗震设计中推广使用.
此外,美国加利福尼亚州CALTRANS桥梁抗震设计规范依据美国下一代衰减关系(NGA)计划建立的地震动衰减模型提供了在不同震级和剪切波速等条件下的桥梁用光滑反应谱[14],但并没有给出具体的表达式,不易推广.
综上所述,目前仍然没有普适性的统一光滑设计谱,寻找与传统规范设计谱在参数及表达形式上相类似的光滑谱是十分必要的,本文将对此进行研究.
2 统一光滑地震反应谱对于坐落在刚性地基上的单质点弹性体系,应用数值积分方法可求得地震激励下的具有不同频率或周期下的结构响应最大值,从而可先后获得相对位移反应谱Sd、相对速度反应谱Sv、绝对加速度反应谱Sa.当地震动过程足够长时,一般认为可以忽略响应解析表达式中关于阻尼系数的高次项并将正弦函数与余弦函数等价,得到位移反应谱与拟速度反应谱Spv、拟加速度反应谱Spa的关系[15, 16]:
| ${{s}_{\text{a}}}\approx {{s}_{\text{pa}}}\approx \omega {{s}_{\text{pv}}}\approx \omega {{s}_{\text{v}}}\approx {{\omega }^{2}}{{s}_{\text{d}}}.$ | (5) |
由于将正弦函数与余弦函数等价的假定比较粗略,很多地震作用下的拟速度反应谱在低频段与相对速度反应谱的差别比较明显.但由相对位移反应谱Sd反推获得的拟加速度反应谱Spa与绝对加速度反应谱Sa的偏差可以忽略不计.鉴于Sa属于高阶谱,其变化规律相对复杂,可考虑从研究Sd的频谱特性入手获取高阶光滑谱.在地震反应谱中,Sd的规律最为明显和简单,众多研究成果表明[3, 11, 17]:考虑了场地条件和结构阻尼比影响后,一般认为相对位移反应谱可近似用线性模型来表示:
| ${{s}_{\text{d}}}={{a}_{\text{d}}}T+{{b}_{\text{d}}}.$ | (6) |
值得指出的是,上式是具有完全项一次多项式,而多项式是最简单的光滑曲线,且具有无限可微的特性.考虑到式(5)中Sd与Sv的关系以及ω=2π/T,并从函数表达式的完备性上考虑,可构建拟速度反应谱为完全项多项式:
| ${{s}_{\text{pv}}}=\frac{{{a}_{\text{v}}}T+{{b}_{\text{v}}}}{{{c}_{\text{v}}}T+{{d}_{\text{v}}}}.$ | (7) |
纵观式(6)和式(7),虽然式(6)不能展现相对位移反应谱的全部特性,但通过设定式(7)使其成为具有完全项的多项式,从而使得通过式(7)和式(5)换算回相对位移反应谱时,得到的表达式比式(6)更丰富细致,弥补了原有缺陷.依此方法,可获得拟加速度反应谱和绝对加速度反应谱的完全项表达式为
| ${{s}_{\text{a}}}={{s}_{\text{pa}}}=\frac{aT+b}{c{{T}^{2}}+dT+e}.$ | (8) |
上式为光滑曲线,且形式简单,通过合理地设置参数可以较准确地反映加速度谱的变化规律.
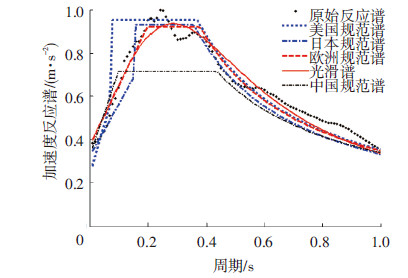
为了验证光滑加速度反应谱的优点,参考美国抗震设计规范中对场地类型的划分要求,本文利用太平洋地震工程研究中心(PEER)数据库,针对每类场地分别选取了世界范围内的70条典型地震记录,采用Runge-Kutta法进行数值计算并进行统计分析,获得了各类场地的弹性加速度反应谱,其阻尼比取为5%.根据不同规范中的加速度反应谱函数,采用Levenberg-Marquardt优化算法对不同场地的均值反应谱进行非线性拟合.其中C类场地的拟合结果见图 1、2.
|
图1 C类场地不同加速度反应谱拟合结果对比(0~1 s) |
|
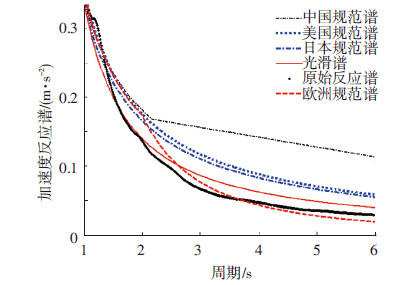
图2 C类场地不同加速度反应谱拟合结果对比(1~6 s) |
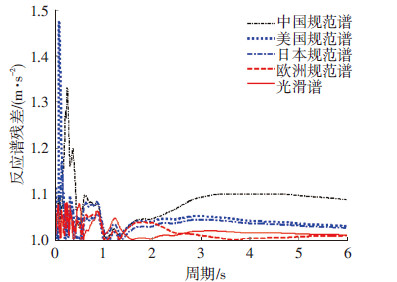
各国或地区规范采用的分段式设计谱由于受规定的特征周期及分段谱函数的所限,在特征周期之内与真实谱的偏差较大;在特征周期之外,欧洲规范谱具有较高的精度,但其他规范谱仍有一定偏差.上述现象在文献[18, 19]中均有所体现和论述.光滑谱不存在明显的特征周期,但在各个周期段上均有良好的逼近性,最接近于真实谱数据.C类场地下各反应谱的残差绝对值(实际谱值与拟合谱值之差的绝对值)见图 3,进一步验证了光滑谱的精确性.
|
图3 C类场地下各反应谱的残差绝对值 |
不同场地下各谱的加速度反应谱拟合残差绝对值和见表 1.对于所有场地类别,光滑谱均表现出了优越的拟合性能,适合作为设计反应谱的参考形式.此外可以看出,欧洲规范谱也具有较好的精度,日本及美国规范虽然有一定偏差,但偏于保守,而中国规范谱在短周期和长周期段的残差均较大,需要考虑进行适当调整.
| 表1 不同加速度反应谱拟合残差和 |
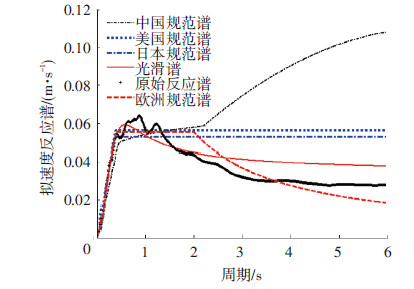
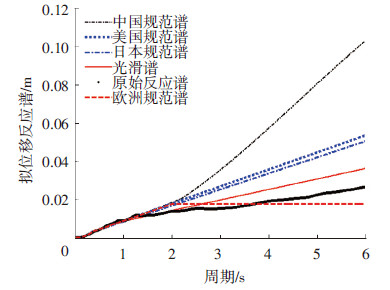
根据式(5)将各加速度谱转换为拟速度谱和拟位移谱分别见图 4、5.与其他规范反应谱换算得到的结果相比,可以认为由加速度光滑谱获得的低阶光滑谱仍然具有较高的精度.
|
图4 不同加速度反应谱对应的拟速度谱 |
|
图5 不同加速度反应谱对应的拟位移谱 |
式(8)中,不同参数均能影响加速度光滑反应谱的幅值.此外,调整b还可以改变反应谱的初始值,调整c、d和e可以影响峰值部分谱形的宽窄.不同场地条件下归一化后的加速度光滑反应谱的拟合参数见表 2,可见除a之外参数的变化具有明显的规律性.
| 表2 不同场地条件下归一化加速度光滑反应谱拟合参数 |
综合考虑各参数的作用并结合目前分段式设计谱的参数选取原则,建议加速度光滑设计谱可采用如下形式:
| ${{s}_{\text{a}}}=\frac{{{\alpha }_{m}}\left( {{a}_{c}}T+{{b}_{c}} \right)}{{{\alpha }_{m}}{{c}_{c}}{{T}^{2}}+{{d}_{c}}T+{{e}_{c}}{{T}_{g}}}.$ | (9) |
式中:αm为地震动加速度峰值,ac~ec为调整后的参数.
弹性加速度光滑谱可通过适当调整转化为弹塑性加速度光滑谱.已有研究成果表明,根据等位移准则,长周期段结构的强度折减系数R与延性系数μ相等[20].本文根据上述规律,同时考虑光滑谱的系数调整特性,可对式(9)分子分母同时除以$\sqrt{u}$并进行适当简化构建弹塑性加速度光滑谱的函数表达为
| ${{s}_{\text{aI}}}=\frac{{{s}_{\text{a}}}}{R}\approx \frac{{{s}_{\text{a}}}}{\mu }\approx {{c}_{m}}\frac{aT\sqrt{\mu }+b}{c\sqrt{\mu }{{T}^{2}}+dT+e}.$ | (10) |
式中:a~b等参数与式(8)中的取值相同,cm为修正系数,建议取值范围为1.0~1.1.
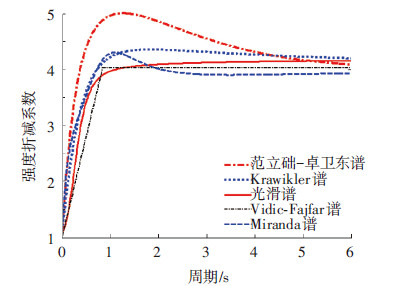
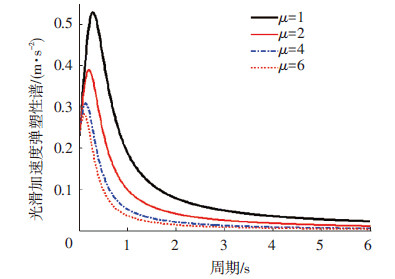
根据式(8)和式(10)的比值可获得光滑的强度折减系数R,将其与国内外建立的典型等延性强度折减系数谱拟合公式进行对比[21, 22, 23, 24].在C类场地下μ等于4时的各强度折减系数曲线见图 6.不同延性下的光滑弹塑性谱见图 7.结果表明光滑强度折减系数曲线与其他模型的变化规律一致,且取值比较均衡.由式(10)获得的光滑弹塑性谱在中长期周期段内具有足够的精度.
|
图6 C类场地下各强度折减系数曲线对比 |
|
图7 不同延性下的光滑弹塑性谱 |
综上所述,光滑地震反应谱具有机理明确、形式简单、拟合精度高等优点,可以在今后的反应谱研究中加以进一步验证、应用并推广.光滑地震反应谱的统一性主要表现为4个方面:(1)函数统一性,将传统的加速度分段式设计反应谱统一表示为一个光滑连续的多项式函数,避免出现拐点及不必要误差,简明实用;(2)多阶谱精度统一性,在拟位移谱和拟速度谱等低阶量上也具有良好的拟合精度,具有较高的协调性;(3)弹塑性谱统一性,能够通过简单的参数设定转换为弹塑性反应谱,同时能确保在中长期周期段内具有足够的精度;(4)多维谱统一性,一般认为竖向加速度反应谱的谱形与水平加速度反应谱的近似,因此光滑谱也同样适合竖向反应谱.此外,根据王君杰等[25]的研究结果,转动反应谱可以根据视波速和平动反应谱获得,因此光滑转动反应谱可由光滑平动反应谱经过简单换算直接获得,最终多维地震动反应谱均可表示为光滑函数形式.
3 考虑多阶谱的地震动合成从大量已有研究成果及前文分析结果可以看出:相对于其他国家的设计加速度反应谱,中国抗震设计规范采用的加速度反应谱的谱值在短周期和中长周期较小,而在长周期部分明显增大甚至反超,因此关于中国抗震设计谱在长周期段的精度及适用性一直存在争鸣[26].虽然这在客观上促进了关于设计谱谱形及阻尼比折减系数等问题的研究,但不断完善抗震设计谱仍是十分必要和迫切的.设计谱的演变是一个随着震害经验和强震记录的积累以及对地震动反应谱特性的不断认识而逐渐深入的过程,中国建筑抗震规范大致经过了五次演变,主要体现在对反应谱的特征周期以及反应谱谱值的不断修正上.在多次演变之后,设计反应谱过于强调经验化,而在一定程度上忽略了精确化和平均化,其主要问题表现为:在早期的设计谱基础上多次修改后,设计谱的谱形与实际均值谱或概率谱仍然存在差异,在某些情况下,这种差异甚至被放大了;为了保证长周期结构的抗震设计具备保守性,人为地增大了长周期段的谱值,而这种方法既不能完全保证对大型复杂结构进行振型组合后得到结构响应的合理性,又导致设计谱在低频段的谱特性失真且各频段之间不协调,由此生成的人工地震动不能充分反映真实地震动的频谱统计特性,最终将影响时程分析结果和抗震设计方案的科学制定.因此,除了针对目前设计谱的不足进行改进之外,也应探讨更有效的人工地震动合成方法.
目前人工地震动合成最常用的方法为基于功率谱的合成法[27],该法按照相关抗震规范并根据地震烈度、场地类别及持时等设计参数确定加速度设计反应谱及功率谱,再由功率谱得到的Fourier幅值谱附加随机相位作Fourier逆变换,最后乘以确定性的强度包线函数得到近似人工地震动.该法具有一定的精度和效率,基本满足工程需求,但也存在不足:(1)仅由加速度谱生成地震动并不能完全保证该加速度时程换算成速度和位移时程后仍符合相关低阶谱的频谱形式及精度需求;(2)由于目前各国抗震规范基本采用分段式设计谱,由此生成的功率谱也是分段式函数形式,存在拐点,不利于拟合过程的迭代和收敛,影响计算效率和精度.
有鉴于此,本文提出了基于统一光滑谱并考虑多阶谱的人工地震动合成方法,其基本思想是利用统一光滑谱的特点,采用交替迭代的方法对人工地震动的加速度谱和速度谱进行同时修正,最终获得同时满足以上两种目标谱的地震动信号.该方法的主要流程:
1) 通过目标加速度反应谱Sa(ω)与加速度功率谱的近似关系式求出功率谱
| ${{G}_{\text{a}}}\left( \omega \right)\approx -\frac{\xi }{\pi \omega }{{\left[ {{s}_{\text{a}}}\left( \omega \right) \right]}^{2}}/\ln \left( \frac{-\pi }{\omega {{T}_{d}}}\ln \ \ p \right).$ | (11) |
式中:ξ为结构阻尼比,ω为结构圆频率,Td为地震动持时,p为计算反应谱的平均幅值不超过目标反应谱幅值的概率系数,一般大于0.85.
将地震动视为平稳过程,结合目标速度反应谱和式(8)计算速度功率谱
| ${{G}_{v}}\left( \omega \right)={{\omega }^{2}}{{G}_{a}}\left( \omega \right).$ | (12) |
2)由加速度功率谱计算加速度Fourier幅值谱
| ${{A}_{a}}\left( \omega \right)={{\left[ 4{{G}_{a}}\left( \omega \right)\Delta \omega \right]}^{1/2}},$ | (13) |
式中Δω为频率间隔.
类似可得到速度Fourier幅值谱
| ${{A}_{v}}\left( \omega \right)={{\left[ 4{{G}_{v}}\left( \omega \right)\Delta \omega \right]}^{1/2}}.$ | (14) |
3) 计算目标加速度反应谱的脉冲响应函数向量,通过Fourier变换求加速度反应谱传递函数向量.
4) 将Fourier幅值谱和随机相位谱Φ(ω)转换成Fourier变换的实部和虚部,并进行Fourier逆变换,可得到近似的人工地震动加速度时程
| $a\left( t \right)=\text{FF}{{\text{T}}^{-1}}\left\{ {{A}_{a}}\left( \omega \right)\exp \left[ \text{i}\Phi \left( \omega \right) \right] \right\}.$ | (15) |
5) 将上式乘以强度包络函数g(t)得到幅值非平稳地震动时程
| ${{a}_{g}}\left( t \right)=a\left( t \right)g\left( t \right).$ | (16) |
6) 对非平稳地震动时程进行Fourier变换并将其与反应谱传递函数向量乘积的逆变换做卷积运算,计算ag(t)的反应谱Sak(ω) (k=1,2,3,…).
7) 用目标加速度反应谱与计算反应谱的比值修改Fourier幅值谱
| ${{A}_{\text{ak+1}}}\left( \omega \right)={{A}_{\text{ak}}}\left( \omega \right)\frac{{{s}_{\text{a}}}\left( \omega \right)}{{{s}_{\text{ak}}}\left( \omega \right)}.$ | (17) |
8) 将Aak+1(ω)代入式(15)并按式(16)进行调整,对新的人工地震动加速度时程进行Fourier变换,对其Fourier分量进行积分获得速度时程vg(t).
9) 计算目标加速度反应谱的脉冲响应函数向量,通过Fourier变换求速度反应谱传递函数向量.
10) 对速度时程vg(t)进行Fourier变换并将其与反应谱传递函数向量乘积的逆变换做卷积运算,计算vg(t)的反应谱Svk(ω) (k=1,2,3,…).
11) 用目标速度反应谱与上述计算反应谱的比值修改Fourier幅值谱,获得新幅值谱
| ${{A}_{\text{vk+1}}}\left( \omega \right)={{A}_{\text{vk}}}\left( \omega \right)\frac{{{s}_{v}}\left( \omega \right)}{{{s}_{\text{vk}}}\left( \omega \right)}.$ | (18) |
12) 对新的人工地震动速度时程进行微分,最终获得新的加速度时程,代入式(15),并重复步骤4)~11)的运算,循环迭代,直到加速度及速度的目标反应谱与计算反应谱各频率成分幅值比均接近1,并满足允许误差要求为止.
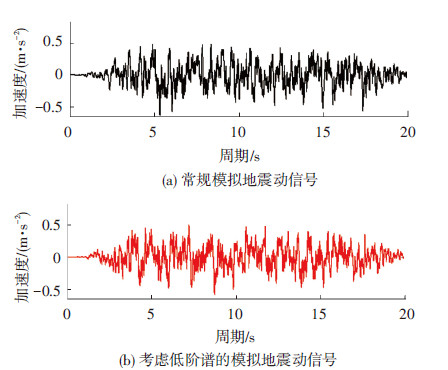
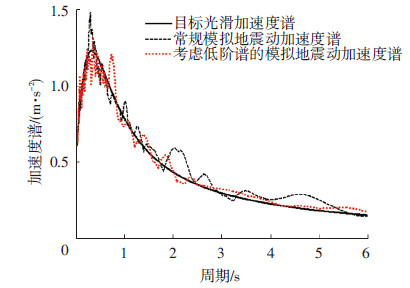
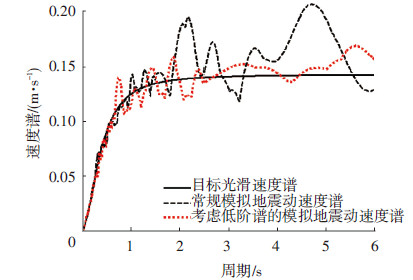
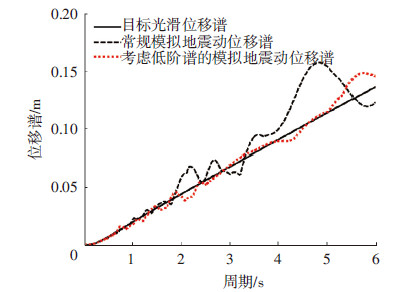
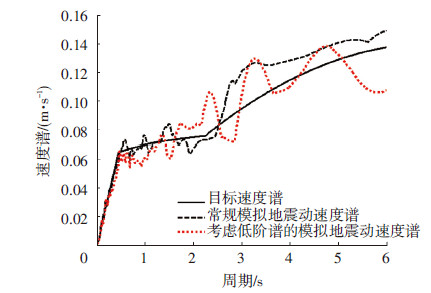
为了验证上述方法的有效性,本文假定某地震动位于Ⅱ类场地土,抗震设防烈度为8度,多遇地震,设计地震分组为第2组,阻尼比为0.05,目标反应谱为相应的光滑谱.人工合成地震动的持时为20 s,式(11)中p取为0.85,采样频率为400 Hz,迭代次数为70次,包络线的上升段和下降段线形均为抛物线.按照上述方法及常规功率谱法合成的加速度信号见图 8,相应的加速度、速度和位移反应谱曲线见图 9~11.结果表明,基于统一光滑谱并考虑多阶谱的人工地震动反应谱与目标谱十分吻合,在相同迭代次数下其精度大于用常规方法.而常规地震动合成方法由于未兼顾多阶谱的需求,其反应谱在长周期段不易收敛到指定精度,与目标谱偏离较大,该现象在速度谱和位移谱中表现更为明显.如果将中国抗震设计规范建议的加速度反应谱作为目标谱进行人工地震动合成,其速度谱见图 12.可以看出,由于规范设计谱本身存在两个明显拐点,且其长周期段需求相对发散,导致即使考虑多阶谱的地震动合成结果也差强人意,由常规方法获得的地震动有时不能完全满足速度谱乃至位移谱的频谱需求.可见,目标谱的连续性和精确性直接影响合成地震动频谱特征的真实性和准确性,今后有必要考虑对中国规范设计谱的谱形进行修正.
|
图8 人工合成的加速度信号 |
|
图9 人工合成地震动的加速度反应谱对比 |
|
图10 人工合成地震动的速度反应谱对比 |
|
图11 人工合成地震动的位移反应谱对比 |
|
图12 由规范反应谱合成的速度反应谱 |
抗震设计谱是通过对原始地震反应谱进行平均化、规准化、平滑化和经验化之后得到的,过程中产生误差在所难免,精确性和适用性强的加速度设计谱应该能够兼顾各周期段的谱值变化规律和精度,同时简便实用,这样不仅能够确保加速度谱与平均反应谱吻合,还能保证其低阶谱不失真.目前绝大部分国家或地区均采用分段式设计谱的形式,而分段式设计谱由于在规准化和平滑化过程中存在不足,导致其精度尚需进一步完善.同时,过度经验化的设计谱可能放大局部周期段的谱值而导致整体的精度和协调性变差.以上不足均可能导致由设计谱合成的人工地震动的频谱特性与真实统计特性不符,对抗震计算及设计造成不利影响.
基于反应谱的基本原理及各阶反应谱的特性提出了统一光滑反应谱的概念,其谱函数为多项式商,实现了用唯一函数表示整个谱形的功能,且其精度较高.统一光滑反应谱的统一性具体体现在函数统一性、多阶谱统一性、弹塑性谱统一性及多维谱统一性等4个方面.
提出的基于光滑谱并考虑多阶谱的人工地震动合成方法能够更准确地符合加速度谱、速度谱和位移谱的频谱特性需求,精度较高.
统一光滑反应谱尚需更深入的研究.地震动是复杂的近地表多维波动,统一光滑反应谱在6 s之外的长周期是否仍能保持足够的精度,能否充分考虑近场的脉冲效应以及远场的衰减现象都需要进行专项研究.统一光滑反应谱在实际结构抗震设计中的应用效果也应将进一步开展研究.
| [1] | BIOT M A. Theory of elastic systems vibrating under transient impulse with an application to earthquake-proof buildings [J].Proceeding National Academy of Sciences, 1933, 19(2): 262-268.( 1) 1) |
| [2] | HOUSNER G W. Calculating the Response of an Oscillator to Arbitrary Ground Motion [J]. Bulletin of the Seismological Society of America, 1941, 31(5): 143-149.( 1) 1) |
| [3] | NEWMARK N M, HALL W J. Procedures and criteria for earthquake resistant design on building research series No.46 [R]. Washington: Dept of Commerce National Bureau of Standards, 1973:209-236.( 2) 2) |
| [4] | 中华人民共和国建设部. 建筑抗震设计规范:GB5001—2010[M]. 北京:中国建筑工业出版社,2010.( 1) 1) |
| [5] | 日本建筑中心. 建筑物的构造规定-建筑基准法施行令第3章的解说与运用[M]. 东京:日本建设省建筑研究所, 1997.( 1) 1) |
| [6] | FEMA 450. NEHRP recommended provisions for the development of seismic regulations for new buildings and other structures [S]. Washington DC: Building Seismic Safety Council for the Federal Emergency Management Agency, 2003.( 1) 1) |
| [7] | Eurocode 8: Design of structures for earthquake resistance-part 1: general rules, seismic actions and rules for buildings [S]. Brussels, Belgium: European Committee for Standardization, CEN, 2004.( 1) 1) |
| [8] | 余湛, 石树中, 沈建文,等. 从中国、美国、欧洲抗震设计规范谱的比较探讨我国的抗震设计反应谱[J]. 震灾防御技术, 2008, 3(2): 136-144. ( 1) 1) |
| [9] | 王段. 结构抗震反应谱的研究[D]. 青岛: 青岛理工大学, 2010.( 1) 1) |
| [10] | 徐龙军, 谢礼立, 胡进军. 抗震设计谱的发展及相关问题综述[J]. 世界地震工程, 2007, 23(2): 46-57. ( 1) 1) |
| [11] | 胡聿贤. 地震工程学[M]. 2版.北京: 地震出版社, 2006.( 2) 2) |
| [12] | INN. Earthquake resistant design of buildings, NCh433.Of96 [S]. Santiago, Chile :Instituto Nacional de Normalización,1996.( 1) 1) |
| [13] | US-NUREG/CR 6728. Regulatory guidance on design ground motions [S]. Washington DC: Nuclear Regulatory Commission, 2001.( 1) 1) |
| [14] | California Department of Transportation (CALTRANS). Seismic design criteria (version 1.7) [S]. Sacramento: California Department of Transportation, 2003.( 1) 1) |
| [15] | CLOUGH R W, PENZIEN J. Dynamics of structures[M]. New York: McGraw-Hill Inc, 1993.( 1) 1) |
| [16] | CHOPRA A K.Dynamics of structures: theory and applications to earthquake engineering[M].New Jersey: Prentice-Hall, 1995.( 1) 1) |
| [17] | 曹加良, 施卫星, 刘文光. 长周期结构相对位移反应谱研究[J]. 振动与冲击, 2011, 30(7): 63-70.( 1) 1) |
| [18] | HEO Y, KUNNATH S, ABRAHAMSON N. Amplitude-scaled versus spectrum-matched ground motions for seismic performance assessment [J]. Journal of Structural Engineering, 2011, 137(3): 278-288.( 1) 1) |
| [19] | BAKER I W. The conditional mean spectrum: tool for ground motion selection [J]. Journal of Structural Engineering, 2011, 137(3): 322-331.( 1) 1) |
| [20] | VIDIC T, FAJFAR P, FISHINGER M. Consistent inelastic design spectra: strength and displacement [J]. Earthquake Engineering and Structural Dynamics, 1994, 23(5): 507-521.( 1) 1) |
| [21] | KRAWINKLER H, RAHNAMAM. Effects of soil on design spectra [C]// Proceeding of 10th World Conference on Earthquake Engineering. Madrid, Spain:[s.n.], 1992: 5841-5846.( 1) 1) |
| [22] | MIRANDA E, BERTERO V. Evaluation of strength reduction factors for earthquake-resistant design [J]. Earthquake Spectra, 1994, 10(2): 357-379.( 1) 1) |
| [23] | 卓卫东, 范立础. 结构抗震设计中的强度折减系数研究[J]. 地震工程与工程振动, 2001, 21(1): 84-88.( 1) 1) |
| [24] | CUESTA I, ASCHHEIM A, FAJFAR P. Simplified R-factor relationships for strong ground motions [J]. Earthquake Spectra, 2003, 19(1): 25-45.( 1) 1) |
| [25] | 王君杰, 江近仁. 地震动旋转分量的反应谱估计[J]. 地震工程与工程振动, 1993, 13(11): 7-16.( 1) 1) |
| [26] | 曹加良, 施卫星, 何文福. 新抗震规范反应谱的适用性研究[J]. 振动与冲击, 2011, 30(11): 79-84.( 1) 1) |
| [27] | 田玉基, 杨庆山. 多阻尼比设计反应谱的非平稳地震动场拟合 [J]. 振动与冲击, 2010, 29(1): 87-91.( 1) 1) |
 2016, Vol. 48
2016, Vol. 48


