2.结构风工程与城市风环境北京市重点实验室,100044 北京
2.Beijing’s Key Laboratory of Structural Wind Engineering and Urban Wind Environment, 100044 Beijing, China
由于受荷载的作用和各种突发因素(如台风、地震、火灾、爆炸等)的影响,工程结构在使用过程中往往会发生不同程度的损伤和破坏.中国现行抗震规范中抗震设计的原则是:小震不坏,中震可修,大震不倒.按照这一原则设计的建筑物在受中震以上地震时往往会受到不同程度的损伤.人们越来越意识到研究结构损伤的重要意义,它不仅可以评估结构所处工作状态是否安全,而且可以为进一步制定加固措施提供技术依据[1].
长期以来,相关学者针对结构的损伤识别提出了多种方法,其中对振动模式的识别和结构响应信号在时域、频域内的转换处理一直是该领域的研究热点和难点[2, 3].小波变换在时域和频域都具有良好的局部化性质,较好解决了时间和频率分辨率的矛盾,对信号的低频成分,可用宽时窗使得时域分辨率低而频域分辨率高;对信号的高频成分,则可用窄时窗使得时域分辨率高而频域分辨率低,可聚焦到信号的任意细节进行时频域处理[4].小波分析这种自适应分辨分析的优良性质,非常适合结构振动状态的诊断,可用于结构损伤的识别.
Gokdag等[5]提出一种新的基于小波变换的损伤识别方法,通过离散小波变换从损伤结构中提取并构造适当的未损结构近似函数.由此通过损伤结构模态的连续小波变换系数以及其近似函数的差值,定义一个可靠的损伤指数来识别损伤;Hong等[6]利用小波奇异性对裂缝梁进行了损伤检测,首先利用小波变换对梁的一阶模态振型进行了连续小波分析,然后通过数值模拟,可准确诊断出损伤位置,以奇异性指数为指标,诊断梁损伤的程度;Solis等[7]提出了一种通过模态振型变化识别损伤位置的方法,通过对未损以及发生损伤结构的模态振型向量差进行小波变换,把所有模态振型向量差的小波变换结果相加来识别结构的损伤位置.最后通过对存在不同大小和位置裂缝的钢梁进行试验分析,表明该方法对损伤很敏感,同时还研究了损伤阈值以及成功识别损伤所需的传感器数量;Hou等[8]利用小波分析理论对ASCE基准结构的损伤监测问题进行了研究,分析过程中将多个节点加速度进行小波分解,并通过分解后突起结点在整个结构中的空间位置来判断损伤位置;李洪泉等[9]对框架结构在地震作用下的损伤位置进行了振动台试验研究,对比结构损伤前后各层加速度响应小波尺度图的变化判断出结构的损伤位置;Hester等[10]建立了车辆-桥耦合有限元模型,提出了一种基于每个截面振动信号的小波能量的损伤识别方法,并且证明了这种方法识别结构损伤较之前研究者提出的小波系数方法更加敏感.
目前小波分析主要针对简单结构损伤诊断的数值模拟和试验研究,例如带裂缝的简支梁,平面框架等.但是对于空间框架,乃至更复杂的结构,特别是损伤位置的精确定位,国内外的研究较少.小波包能量曲率具有更加敏感的识别能力,本文通过这一指标比较了不同响应信号对损伤识别的敏感性以及有限元模型网格划分尺寸、所取时程反应信号的位置和采样频率对损伤位置的识别结果的影响.
1 小波分析理论 1.1 多分辨率分析传统的Fourier分析在时域上没有任何局部化特征,小波变换不同于Fourier变换的地方是,它在时域和频域都具有良好的局部化性质,非常适合对含有稳态和非稳态成分的信号进行时频分析[11].
对于一个能量有限的函数f(t),即满足f(t)∈L2(R),它的连续小波变换为
| ${{W}_{f}}\left( a,b \right)=< f\left( t \right),{{\psi }_{a,b}}\left( t \right)>=\frac{1}{\sqrt{\left| a \right|}}\int\limits_{-\infty }^{\infty }{f\left( t \right)\psi \overline{\left( \frac{t-b}{a} \right)}}dt,$ | (1) |
式中:a,b分别为尺度因子和平移因子,a,b∈R,且a≠0,ψa,b(t)是母小波ψ(t)经过尺度伸缩与时间平移所生成的小波函数族,即小波基:
| ${{\psi }_{a,b}}\left( t \right)=\frac{1}{\sqrt{a}}\psi \left( \frac{t-b}{a} \right),$ | (2) |
| ${{C}_{\psi }}=\int\limits_{-\infty }^{\infty }{\frac{{{\left| {{F}_{\psi }}\left( w \right) \right|}^{2}}}{\left| w \right|}dw< w.}$ | (3) |
式中Fψ(w)是ψ(t)的傅里叶变换.
虽然多分辨率分析是种有效的时频分析方法,但是在高频段其频率分辨率较差,而在低频段其时间分辨率较差.小波包分析能够为信号提供一种更加精细的分析方法,它将频段进行多层次划分,对多分辨率分析没有细分的高频部分进一步分解,在不同频段均可得到高分辨率.对于函数f(t),其小波包变换为
| $C_{j,k}^{i}\left( t \right)< f\left( t \right),\psi _{j,k}^{i}\left( t \right)>,\ \ i=1,2,\cdots ,L.$ | (4) |
式中:Cj,ki(t)称为小波包系数,i、j、k分别是频程参数、尺度参数和平移参数,ψij,k(t)为小波包函数,即
| $\psi _{j,k}^{i}\left( t \right)={{2}^{-j/2}}{{\psi }^{i}}\left( {{2}^{-j}}t-k \right),$ | (5) |
式中:i=0,1,…,L,L=2j-1,ψij,k(t)可以由母小波函数ψ(t)逐次计算得到.
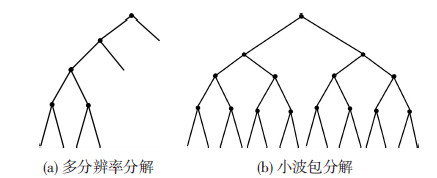
1.2 小波包能量广义的小波分析包括小波多分辨率分析和小波包分析,它们的分解结构树见图 1[12].
|
图1 小波分解的结构树 |
实际上,小波包的分解经常用在能量检测中.Sun 等[13]提出了小波包信号分量的能量计算方法,并证明利用信号分量的能量比直接利用小波包系数能够得到更具有鲁棒性的信号特征.小波包信号分量的能量一般定义为
| ${{E}_{f_{j}^{i}}}=\int_{-\infty }^{\infty }{f_{j}^{i}{{\left( t \right)}^{2}}dt,}$ | (6) |
式中Efji表示信号分量fji(t)的能量.一旦结构发生损伤,那么结构响应信号的一些频段一定会发生波动,这样按照小波包分解的信号分量中的一个或者几个分量一定会发生能量的改变.根据这一原理,可利用小波包能量分量的变化来进行损伤识别.
2 有限元模型建立本模型引用文献[14]中的试验模型,为一3层钢筋混凝土框架结构,整体尺寸为1 000 mm×1 000 mm×2 400 mm,梁、柱截面尺寸为70 mm×70 mm,板厚为70 mm,混凝土密度ρ=2 450 kg/m3,泊松比为0.2,弹性模量为30 GPa.该模型的地震损伤试验在同济大学土木工程防灾国家重点实验室4 m×4 m模拟地震振动台上进行.
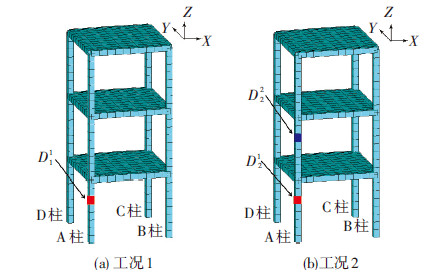
在ANSYS数值模拟中,Beam4单元是一种可承受拉、压、弯、扭的单轴受力三维空间刚架单元,一般用来模拟具有空间自由度的梁柱构件.shell63单元是一种弹性壳单元,可承受平面内及法线方向的荷载,与楼板的受力状态相似.故使用beam4单元模拟框架梁柱,用shell63单元模拟楼板.经试算,网格尺寸为10 cm左右时,结构动力特性的分析结果和实验结果计算频率与试验频率接近,故确定基本有限元模型每层柱划分为8个单元.模型中Beam4单元共计216个,shell63单元共300个.分两种损伤工况进行模拟,将结构的特定位置的材料弹性模量进行改变来模拟损伤,损伤工况详见表 1和图 2.表 2、3为数值模拟与实验实测主要结果的对比,表明了本文所建有限元模型的合理性和分析方法的可靠性,图 3是结构的X向前三阶模态振型.
| 表1 两种损伤工况 |
|
图2 两种损伤工况 |
| 表2 结构前两阶自振频率 |
| 表3 结构顶层加速度峰值 |

|
图3 X向前三阶模态振型 |
需要说明的是上述两种损伤情况对于整个结构的刚度影响非常小.例如,未损有限元模型X向抗侧刚度为1 197.6 kN/m,而工况1时,其有限元模型X向抗侧刚度为1 190.5 kN/m,结构整体抗侧刚度仅减小了0.59%.
3 损伤指标敏感性比较 3.1 小波系数差从形式上来说,小波变换Wf(a,b)本质上表明的是原函数或信号f(t)在x = b点附近按Ψa,b(t)进行的加权平均,它体现的是以Ψa,b(t)为标准f(t)的快慢变化情况,函数f(t)的微小突变将引起小波变换系数比较大的变化[11],这正是本节提出的损伤识别方法的依据.
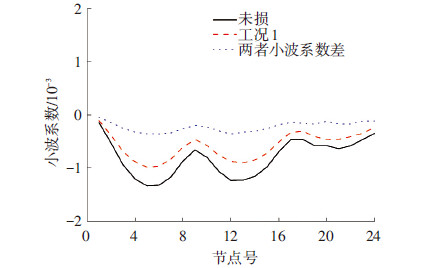
分别将未损时和工况1的一阶振型位移用matlab小波工具箱中的haar小波进行小波连续变换,得到未损和工况1所对应的小波系数.一阶振型的小波系数差见图 4.
|
图4 工况1一阶振型小波系数差 |
从图 4基本上无法判断损伤发生节点6、7处出现峰值变化,同样二阶振型与三阶振型也无法很好识别损伤位置,工况2的情况亦是如此,不再赘述.
3.2 小波包能量曲率差运用式(6),通过能量差法[15]可进行损伤的鉴别,但是为了扩大识别的效果,运用曲率方法进行分析,小波包能量曲率定义为
| $E{{_{j,k}^{i}}^{,,}}=\frac{E_{j,k+1}^{i}-2E_{j,k}^{i}+E_{j,k-1}^{i}}{{{l}^{2}}},$ | (7) |
式中:Ej,ki代表第k个采集点所采集信号的fji(t)的能量,l为划分的单元长度.
接下来计算无损结构的小波包能量曲率与损伤结构的小波包能量曲率差:
| $\Delta E_{j,k}^{i}"=E_{j,k}^{i}"-E{{_{j,k}^{i}}^{\left( d \right)"}},$ | (8) |
然后可根据ΔEji″图形判断损伤位置,图形中的突起处可判断为损伤位置所在处.
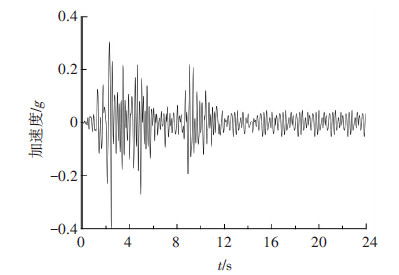
将El-centro地震波输入无损模型与两种损伤工况时的模型x向,峰值加速度为0.4g,进行瞬态时程分析,取样周期为0.02 s,获得发生损伤的A柱各节点的加速度时程响应.图 5为数值模拟方法模拟工况1时顶层加速度响应时程.
|
图5 损伤工况1时顶层加速度响应时程 |
利用matlab中的小波工具箱编程,选取haar小波对得到的信号进行7层小波包分解,得到各节点不同频段上的信号分量fji(t),然后根据式(6)求得分量fji(t)的能量Ef ,再由式(7)、(8)计算出能量曲率差ΔEji″,最后通过小波包能量曲率差来判断损伤位置.因为高频部分容易受到噪音影响,本文选取小波包分解信号的前8个分量来分析.
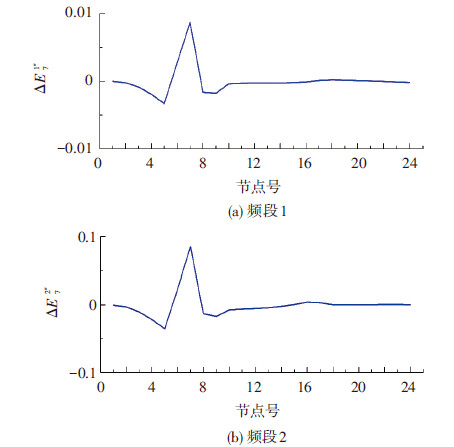
图 6是工况1时各节点加速度时程的1~2频段小波包能量曲率差,3~8频段具有相似的分布变化规律.可以看出,小波包能量曲率差在每个频段上都在损伤D11处发生明显突变,同时也会相应影响到发生损伤的相邻节点,所以可判断损伤发生的位置为D11处.
|
图6 损伤工况1时各节点加速度时程的1~2频段小波包能量曲率差 |
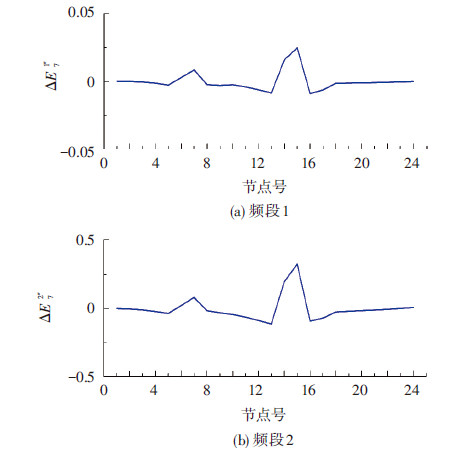
工况2时各节点加速度时程的1~2频段小波包能量曲率差见图 7.和工况1情况相同,3~8频段具有相似的分布变化规律.
|
图7 损伤工况2时各节点加速度时程的1~2频段小波包能量曲率差 |
由图 7可看出,在损伤位置D21、D22处,小波包能量曲率差都具有明显的突变.实际上,在D22处的损伤为50%大于D21处的30%损伤,而在图 7表现为,在D22处的突变程度明显要大于在D21处的突变程度.这表明小波包能量曲率差不但可识别损伤的精确位置,而且对损伤严重程度也具有很好的辨识能力.
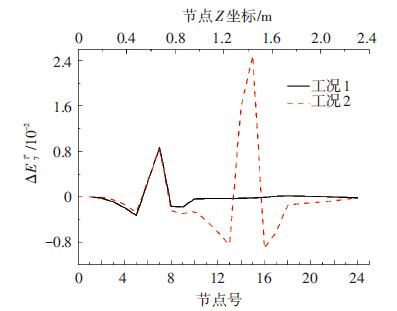
选取工况1和工况2各节点加速度信号第一频段的小波包能量曲率差作为特征代表.图 8表示的是各节点在不同损伤工况下加速度响应第一频段的小波包能量曲率差,从中可明显看出损伤较大的地方突变会更加明显.其余几个频段也具有相似的特征.
|
图8 各节点加速度响应第一频段的小波包能量曲率差 |
以下对节点速度以及位移响应进行小波分析,讨论不同响应作为输入信号时识别损伤的特点.分别以位移、速度、加速度为分析指标,得到各节点的小波包能量曲率差对比,可得到加速度响应第一频段的小波包能量曲率差值在损伤处突变较大,利于损伤的识别.
对每个节点在相同频段的小波包能量曲率差取绝对值求和,再求得各节点在该频段上小波包能量曲率差所占的比例.
| $\mu =\Delta E_{7,k}^{i}"/\sum\limits_{k=1}^{24}{\left| \Delta E_{7,k}^{i}" \right|}.$ | (9) |
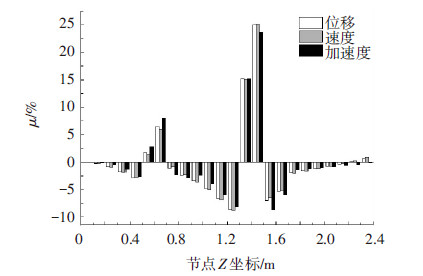
通过式(9)计算得到以加速度、速度、位移响应作为识别数据的各节点小波包能量曲率差百分比μ.然后作出对比柱状图 9,得出分别运用位移、速度和加速度作为分析指标,都能够识别损伤发生位置.从图 9可看出,在高度D21(Z坐标为0.6 m)处,其损伤量较小,加速度信号的识别效果较其他信号的识别效果稍好.这说明损伤引起的刚度微小变化,加速度响应较速度和位移响应敏感.考虑到实际监测环境中,位移响应较小,容易受外界环境影响,抗噪能力不强.所以,在使用小波包能量曲率差进行损伤识别时,加速度响应信号比速度和位移响应信号具有更好的识别效果.
|
图9 损伤工况2第一频段各节点小波包能量曲率差百分比 |
为考察有限元模型的单元划分大小对损伤识别结果存在的影响,取3种网格划分密度的有限元模型分别进行计算.较疏划分为每层4个单元,正常划分为每层8个单元,较密划分为每层16个单元.通过ANSYS瞬态分析,得到各种划分密度模型的柱损伤前和工况1损伤后的节点加速度时程数据,计算小波包能量曲率差百分比.图 10表示3种划分密度各节点小波包能量曲率差百分比.

|
图10 3种划分密度各节点小波包能量曲率差百分比 |
3种网格密度有限元模型损伤单元Z高度坐标都为0.5~0.6 m处.从图 10可看出,正常划分时,Z坐标0.5~0.6 m处的μ都比较大,Z坐标0.4 m处由于受到相邻损伤节点的影响,μ值达到13.8%,其余节点μ值都控制在8%以内;当网格划分得较稀疏时,μ值最大的损伤单元出现在Z高度坐标0.6~0.8 m处,并且在Z坐标0.2 m处单元的μ值达到10%.因此,当网格划分得较疏时,容易对损伤的定位造成一定误差;当网格划分较密时,μ值最大的节点就出现在Z坐标0.5~0.6 m处单元上,并且μ值集中在损伤所在节点处.较密划分时其余节点μ值较其他两种划分方式更小.
因此,基于数值模拟数据下的损伤识别,有限元单元网格划分越密,损伤位置识别的效果将更加可靠,出现明显偏差的可能程度将大幅降低.
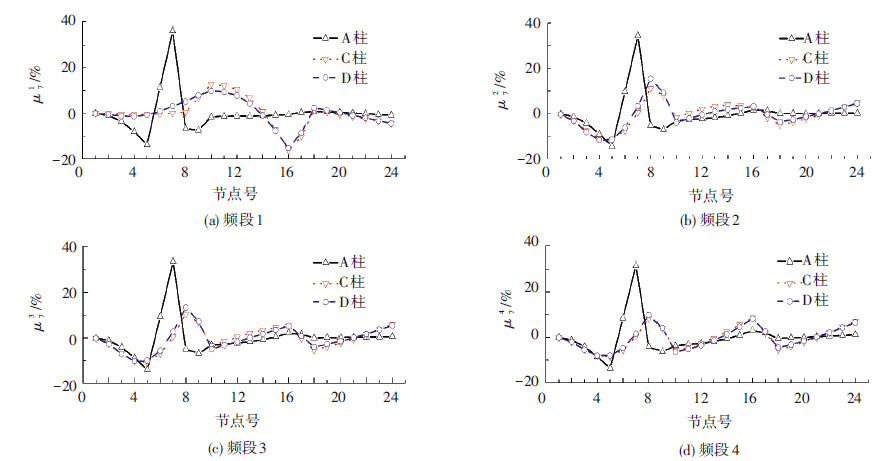
4.2 响应所选节点与损伤柱之间的位置关系根据分析结果,所取的节点不在损伤发生的那列柱上,识别的效果也会受到一定影响.图 11是分别取A、D和C柱上各节点加速度时程数据作为信号,通过时程分析,得到结构没有发生损伤时的节点加速度和工况1下的节点加速度,运用matlab编程计算各节点小波包能量曲率差,然后运用式(9)计算出每个频段上各节点小波包能量曲率差百分比.
|
图11 损伤工况1不同位置柱节点加速度响应的小波包能量曲率差百分比 |
图 11中,C柱与D柱在损伤发生高度处没有极大值点,损伤位置识别不出.但是,除第一频段外,在每一层高的节点处,出现了峰值突变.这是因为发生损伤框架柱通过框架梁的传递,对楼层节点的影响要大于其他节点.结果表明,响应信号采集点的选取,对运用小波包能量曲率差方法识别损伤位置有较大影响.采用损伤所在的A柱节点响应分析时,能精确得到损伤的位置;而采用未发生损伤的其他柱节点响应分析时,仅能识别到损伤所在的楼层.而且,所选柱与损伤柱的距离越近,识别效果越明显.
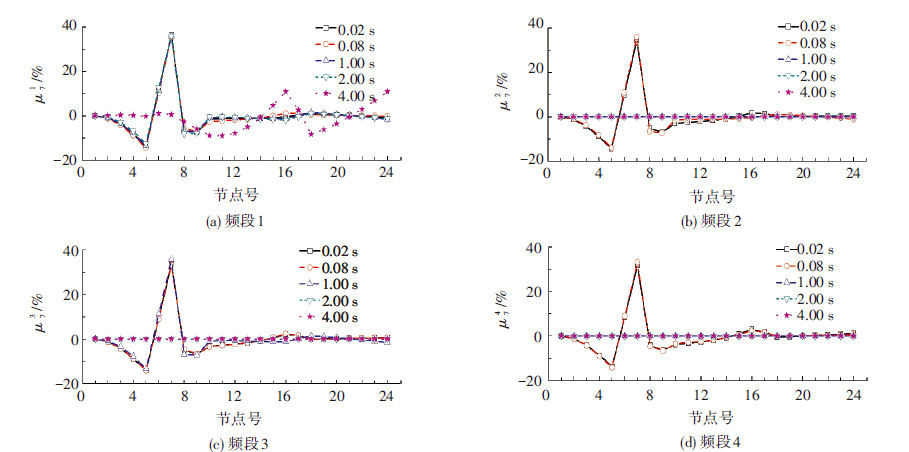
4.3 采样周期对损伤识别的影响为了研究损伤工况1下采样频率对小波包能量曲率差这种算法的影响,将采样周期分别扩大到0.08、1 、2 、4 s下,得到A柱损伤前和工况1下节点加速度响应,通过小波包能量曲率差,由式(9)计算各节点在各频段上小波包能量曲率差百分比,见图 12.
|
图12 损伤工况1时不同采样周期加速度响应的小波包能量曲率差百分比 |
不同采样周期的小波包能量曲率差百分比分布图表明,即使是在0.08 s采样周期以下,小波包能量曲率差峰值突变在1~8频段都很明显.然而当采样周期为1 s或2 s时,只在部分频段出现峰值突变.直至采样周期到4 s时,在损伤部位没有明显的突变出现,因此,当采样周期大于4 s时,加速度响应时程无法识别损伤位置.
5 结 论1)直接使用小波系数差法无法识别损伤发生的位置,而使用小波包能量曲率差法,可以很好判断损伤位置,并且损伤程度越大,峰值突变越明显,能够较好达到损伤识别的目的.
2)不同响应数据作为分析指标时,运用本文方法进行损伤位置识别,以加速度响应数据作为识别信号的识别效果较好.对于损伤引起的刚度微小变化,加速度响应较速度和位移响应敏感.
3)基于数值模拟数据下的损伤识别,有限元单元网格划分越密,损伤位置识别的效果将更加可靠,出现明显偏差的可能程度将大幅降低.
4)采用损伤所在的A柱节点响应分析时,能精确得到损伤的位置;而采用未发生损伤的其他柱节点响应分析时,仅能识别到损伤所在的楼层.进一步,所选柱与损伤柱的距离越近,识别效果越明显.
5)采样周期对损伤位置的识别存在一定的影响,在采样周期为0.08 s及以下时,小波包能量曲率差峰值突变在1~8频段都很明显.当采样周期取4 s及以上时,加速度响应的小波包能量曲率差方法无法识别损伤位置.
| [1] | 杨秋伟. 基于振动的结构损伤识别方法研究进展[J]. 振动与冲击, 2007, 26(10): 86-91.( 1) 1) |
| [2] | FAN W, QIAO P. Vibration-based damage identification methods: a review and comparative study [J]. Structure Health Monitoring, 2011, 10(1): 83-111.( 1) 1) |
| [3] | SIDDIQUE A B, SPARLING B F, WEGNER L D. Assessment of vibration-based damage detection for an integral abutment bridge [J]. Canadian Journal of Civil Engineering, 2007, 34(3): 438-452. ( 1) 1) |
| [4] | 孙增寿, 韩建刚, 任伟新. 基于曲率模态和小波变换的结构损伤位置识别 [J]. 地震工程与工程振动, 2005, 25(4): 44-49.( 1) 1) |
| [5] | GOKDAG H, KOPMAZ O. A new damage detection approach for beam-type structures based on the combination of continuous and discrete wavelet transforms[J]. Journal of Sound and Vibration, 2009,324:1158-1180.( 1) 1) |
| [6] | HONG J C, KIM Y Y. Damage detection using the Lipschitz exponent estimated by wavelet transform applications to vibration modes of a beam [J]. International Journal of Solids and Structures, 2002, 39: 1803-1816.( 1) 1) |
| [7] | SOLIS M, ALGABA M, GALVIN P. Continuous wavelet analysis of mode shapes differences for damage detection [J]. Mechanical Systems and Signal Processing, 2013, 40: 645-666.( 1) 1) |
| [8] | HOU Z, NOORI M, AMAND R. Wavelet-based Approach for Structural Damage Detection [J]. Journal of Engineering Mechanics, ASCE, 2000, 126(7): 677-683.( 1) 1) |
| [9] | 李洪泉, 董亮, 吕西林. 基于小波变换的结构损伤识别与试验分析[J]. 土木工程学报, 2003, 36(5): 52-57. ( 1) 1) |
| [10] | HESTER D, GONZALEZ A. A wavelet-based damage detection algorithm based on bridge acceleration response to a vehicle [J]. Mechanical Systems and Signal Processing, 2012, 28: 145-166.( 1) 1) |
| [11] | LAW S, LI X, LU Z. Structure damage detection from wavelet coefficient sensitivity with model errors [J]. Journal of Engineering Mechanics, 2006, 132(10): 1077-1087.( 2) 2) |
| [12] | 郭健, 顾正维, 孙炳楠,等. 基于小波分析的桥梁健康监测方法[J]. 工程力学, 2006, 23(12): 129-135.( 1) 1) |
| [13] | SUN Z, CHANG C C. Structural damage assessment based on wavelet packet transform [J]. Engineering Structure, 2002, 128(10): 1354-1361.( 1) 1) |
| [14] | 李洪泉, 吕西林. 钢筋混凝土框架地震损伤识别与采用耗能装置修复的试验研究[J]. 建筑结构学报, 2001, 22(3): 9-14.( 1) 1) |
| [15] | 葛继平, 李胡生. 基于小波包能量累积变异的梁桥损伤识别试验[J]. 振动、测试与诊断, 2011, 31(1): 85-88.( 1) 1) |
 2016, Vol. 48
2016, Vol. 48


