公交线网设计是公共交通规划的第一步,也是最重要的一部分[1] . 近50年来,基于公交出行OD与图论的经典公交线网设计理论体系成为主流,并取得了丰富的成果. 虽然其具有直观性、精确性、科学性等优点,也被广泛的应用于实践,但其庞大的计算负担限制了公交线网设计的应用场景:多数研究为局限在一定区域范围内的算例分析[2-3] . 因此近些年来,围绕一个城市范围内公交线网应当如何设计,以及设计方案如何符合城市的布局形态,不断有学者试图通过新的方法、模型来求解. 而在现实情况中,为了改善城市发展不均衡、交通拥堵严重等情况,像北京这样的大城市正不断出台如“京津冀一体化发展”、“通州行政副中心建设”等政策,积极进行城市布局形态的调整. 公交线网从形态、结构、功能都需要符合不断变化的城市布局. 因此,面向城市布局形态的公交线网设计研究也具备很强的现实意义. 基于上述考虑,本文首先对经典公交线网设计研究历程进行简要的总结归纳,而后对近年来面向城市布局形态的公交线网设计研究进行详细综述,并提出未来该领域的研究方向.
1 经典公交线网设计公交线网设计问题是一个典型的NP-Hard问题[4],其描述在已知道路网条件、客流条件以及公交场站(包括首末站、中间站等)的情况下,按照一定的约束条件、目标确定合理的公交线路走向,以满足乘客的出行需求. 1986年,Ceder等[1] 对公交线网设计问题进行了较为系统的归类,提出公交线网设计问题应涵盖:需求特征、目标函数、约束条件以及解法. 2001年,Ceder[5]又将他提出的公交线网设计问题归类为乘客出行模拟、理想线网设计和数学规划模型. 2006年,Fan等[6]通过大量的理论与实践研究,将公交线网设计问题总结为3类:1)以实际经验为主的设计;2)理想条件下的最优化设计;3)基于启发式算法的现实网络设计.
1.1 目标公交线网设计的目标是通过最小的成本投入来最大化地实现公共交通在城市交通系统中的作用. 总结过去几十年来的研究成果,线网设计的目标通常包括乘客利益最优化、运营商利益最优化、乘客和运营商总利益最优化、节能减排最优化、某些特殊变量的最优化等[7-13] . 1986年,Ceder和Wilson[1] 在研究中将乘客出行时间和费用的最小化以及公交服务供给的最大化作为最基本的目标函数. 2000年,Van Nes等[9]研究表明最小化的乘客与运营商的总费用才是最简单有效的目标,如果过度追求效益的最大化,会导致公交线网的吸引力逐步下降. 2006年,Fan等[6] 指出线网设计的最终目标应当是让公交线网在有限的资源条件下发挥最大化服务功能. 此外,不少学者将新能源、环境保护等理念引进到公交线网设计的目标中[10-13].
1.2 变量公交线网设计的变量通常包括决策变量以及其他变量. 决策变量是直接决定公交线网形态、线路运营策略的核心,通常包括公交线网的拓扑结构、公交发车频率以及公交车型等. 早期决策变量的确定通常是在固定线型模式的条件下,即在预定的平行或者放射状的线型结构中,求得最优化的线路空间走向以及发车频率[14-15] . 之后的研究逐步扩展为完善线网拓扑结构以及服务频率的优化,并将费用最小化的概念引入到决策变量的确定过程中[16-17] . 其他变量虽不能直接决定公交线网的形态,却能间接的反映公交线网的运营环境、功能特征以及服务水平等,如乘客出行需求特征、运营模式、公交发展战略等. 近年来,随着灵活公交、动态开线等理念不断发展,变量的灵活多变性在不断拓展延伸,在增加研究复杂性的同时,也更贴合精细化公交服务的理念[18] . 从需求灵活化的角度,2001年,Chien等[19]认为公交出行需求会受到出行时间、出行费用、发车间隔等因素的影响,阐明了公交线网设计过程中的关键变量可以引导公交乘客的出行. 2005年,Lee等[20]认为灵活的公交线网设计方案应依据乘客总出行需求的变化情况决定. 2007年,Quadrifoglio等[21]在洛杉矶研究了根据需求实时更新的线路动态开线策略. 2014年,张玉绣[22]对深圳市小支线巴士服务模式进行研究,研究了对于小型支线如何采取更灵活的运营服务模式,以便更高效地服务于小出行群体. 另外,大站快车作为灵活运营组织方式的一种,近年来被不断深入研究[23-26] .
1.3 算法对于公交线网设计问题的求解常用的算法包括两类,分别是基于一般分析模型的解析式算法和融汇了人工智能与计算机技术的启发式算法. 对于解析式算法,一般是研究线网间距、线路长度、车辆速度、车辆满载率、车队规模、发车间隔等因素之间的内在关系,研究适用场景为路网结构简单、较大范围内公交线网的关键参数确定,常用于偏宏观公交线网设计问题,其算法并不注重于对线路具体走向与路由的确定. 启发式算法是通过一定直观或经验构造算法,并辅助计算机的强大计算能力从庞大的解空间里得到最优解或近似最优解,因此对于现实路网和半现实路网上的公交线路走向、发车间隔等变量的最优化问题有着较好的适用性. 在公交线网设计的研究中,常用的启发式算法包括遗传算法、蚁群算法、模拟退火算法、禁忌搜索算法以及多种算法的嵌套与组合[27-37] .
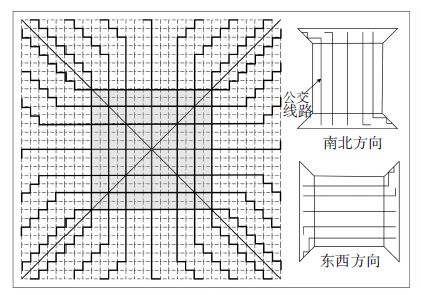
2 面向城市布局形态的公交线网设计 2.1 理论体系概述面向城市布局形态的公交线网设计,是以不同城市布局形态为依托,设计符合形态特征的公交线网方案,常用于较大范围的公交线网设计. 早期有学者如Dickinson[38] 和Lynch[39] 将城市的布局形态定义为两种类型:1)不规则的城市布局,即城市的道路网呈无序的发展状态;2)规则的城市布局,即城市的道路网呈现一定的几何构型. 由于早期城市规模发展有限且功能结构较单一,因此公交线网设计的研究中并未将城市的布局形态作为重要的考虑因素,线网结构的设计也通常是针对简单的放射状或方格网状结构[40-41] . 而随着城市形态布局、功能结构的日益复杂化,城市的发展越来越对公交线网的发展产生影响与制约,较大区域内公交线网与城市布局形态的协调也成为公交线网设计亟需解决的问题. 2010年,Daganzo[42]首次较为系统地阐述了面向城市布局形态的公交线网设计理论体系. 该理论体系在传统公交线网设计的基础上,对线网结构、决策变量、出行需求和求解算法均有一定的突破与创新,使得整个方法体系可以较好地解决与城市布局形态相协调的大规模线网设计问题. 他提出对一个城市范围内的公交线网进行设计时,线网结构应当首先与城市的布局结构相符,并测试了“网格+轴辐式”的线网结构,如图 1所示[42] . 其中,城市中心区采用网格式结构,外围区域采用轴辐射的形式,并通过发车间隔、公交线间距、公交线网覆盖率等3个决策变量来确定线网设计方案.
|
图 1 “网格+轴辐式”线网结构 Figure 1 “Grid+ hub-and-spoke” transit network layout |
为了解决大区域的问题,Daganzo不再运用传统的将需求离散化处理成公交OD的方法,而是利用一类连续近似模型(continuous approximation models,CA)将出行需求设定为随空间呈均匀分布. 这样的处理虽然较理想化,但是避免了大量的OD输入所带来的复杂计算,也改善了将乘客离散化的集计在OD点上与实际不相符的情况. 虽然Daganzo对于出行需求只是采取一种理想化的简化处理,但为解决城市范围内的公交线网设计问题开辟了新的思路,也被广泛地借鉴. 基于这种思想,线网设计的主要目的是确定线路之间合理的空间间距及服务频率. 同时,该思想使得线网设计模型的决策变量较为简化,因此通常可以通过解析方法得到最优解. 该方法适合于长期的战略性线网发展决策,例如线网整体发展布局、结构等的确定[43] .
面向城市布局形态的公交线网设计理论体系自提出后受到了广泛关注,世界各地学者也在不断地补充与优化该理论体系的研究,包括对更加丰富的公交线网结构进行研究,如网格状、放射式、轴辐射式、环形式以及不同形状的组合式线网结构. 而后研究又重点对公交出行需求的变化性以及布线方式的灵活性进行完善. 本文也相应对理论体系中这三方面研究取得的进展进行着重分析.
2.2 线网结构的研究与发展2011年,Estrada等[44]在理想化的城市道路几何形状的基础上,将Daganzo研究中的线网结构拓展到“矩形+轴辐式”,并设计了一类高性能的公交网络,在巴塞罗那市得到运用. 由于线网结构的变化,模型的决策变量增加为:站间距、水平与竖直方向的线路间距、水平和竖直方向中心区与城市总长度的比、发车间隔等,其核心思想与建模求解过程与Daganzo的方法基本类似. 同时通过仿真平台模拟了城市的公交线网形态,并得到了更为精确的费用与服务水平优化结果. 结果显示所设计的高性能公交系统可以提高乘客37%的出行速度,并且降低公交公司的总运营成本.
2014年,Badia等[45]针对莫斯科、巴黎、马德里、阿姆斯特丹、米兰、柏林等城市环形放射状的城市布局形态进行了深入剖析,提出了中心区是同心圆、四周是轴辐式结构的高性能公交线网设计方案,同样将公交出行需求处理为均匀分布. 模型的决策变量共有6个,其中5个为决定公交线网的拓扑形状,包括:中心区辐射线的角度、中心区辐射线的站间距、环形线的长度、环形线的站间距以及中心区域半径,另一个决策变量为发车间隔. 另外作者还针对决策变量、输入参数、出行需求、运输方式、线网结构等进行了敏感性分析. 结果表明该线网结构对发车频率的要求较高,在实验场景中任何情况下,当发车间隔超过5 min都会对整个线网的承受能力造成影响.
2.3 出行需求的研究与发展2013年,Ouyang等[3]以出行需求模型为研究重点,研究在公交出行需求随着空间布局呈不同变化的场景下,构造了符合城市布局形态的混合网格公交线网结构. 通过主干线路与局部线路的配合设计,在公交出行需求大的区域,构造了不同等级局部高密度公交线网. 研究设定主干线从城市的一边贯穿至另一边,而局部线可以起止于城市的任何地点. 线网设计目标是达到企业与乘客成本的最小化. 决策变量包括公交线网几何形态、局部高密度网络几何形态以及公交发车间隔. 通过研究发现这种混合的公交线网结构可以减少公交企业和乘客的成本,原因是在公交需求高的区域,拥有更高密度的公交线网能够显著减少乘客的步行成本.
2015年,Chen等[46]对两种类型城市形态布局下的公交线网结构(环形放射状和网格状)进行了对比研究,并相应建立了两类CA模型. 两种结构下,均为中心城区布设公交干线、城市边缘区布设公交支线. 研究的重点放在公交出行需求的差异与公交服务水平的差异性上. 通过更大范围的场景模拟,研究发现城市边缘区到中心区的距离、中心区与边缘区边界的位置可以显著影响整个线网的服务水平. 由于环形放射状的线网结构更利于乘客基于最短路径的出行,因此可节约9%到13%的总成本,也被认为是一种更有利于公交线网发展的布局形态. Chen等从对比分析的角度研究了环形放射状和网格状线网形态,也提出了更加完善的基于CA模型的线网设计流程.
2.4 灵活布线的研究与发展2012年,Nourbakhsh等[47]在Daganzo“网格+轴辐式”公交线网结构的基础上,构建了一类基于需求响应的动态公交线网体系,该体系下部分公交线路可以在特定的区域内以不固定的路线行驶. 模型的决策变量包括公交线网的几何形状、灵活公交的覆盖区域以及发车频率. 本文假定在研究区域内,公交乘客的出行需求呈独立的泊松分布. 模型的目标函数是企业和乘客的总成本最小. 在城市中心的网格内的公交服务水平要高于边缘轴辐式的线网服务水平. 通过算例分析,带有灵活线路的“网格+轴辐式”公交线网结构能通过减少乘客步行到公交站的距离而提高整个线网的运行效率. 通过与固定线路线网的对比分析,研究表明对于中低公交需求的公交线网体系,带有灵活线路的线网结构能够显著降低企业的运营成本. 2014年,王振报等[48]提出了针对方格形路网布局的多层级的公交线网设计方案. 研究将多等级公交线路与公交换乘枢纽结合,表现为主线、辅线和补充线的灵活组织. 该线网结构的决策变量包括公交主线间距、快线站距和交通分区大小,并从出行者、运营企业和政府管理者三者角度出发建立最优化模型. 最后根据中国大城市具有的出行特征共性,进行了算例分析.面向城市布局形态的公交线网设计研究总结如表 1所示.
| 表 1 面向城市布局形态的公交线网设计研究总结 Table 1 Summary of the studies on transit network design based on the city layout |
由于其模型简单,输入变量、参数较易获取且与实际情况联系紧密,因此在提出后被迅速应用到世界各地. 2012年,Cipriani等[49]通过分析具有弹性的公交出行需求来解决公交线路设计问题,并在罗马成功应用. 2014年,MirHassani等[50]运用类似的思想,在德黑兰设计了网格状的BRT系统. 2016年,Trapote-Barreira等[51]设计了环形+放射状的公交线网结构,并在法国莱里达进行了应用,结果表明改进的线网结构可以为公交运营商节省18%的运力资源,并为乘客节约了10%的成本支出.
3 结论与展望面向城市布局形态的公交线网设计基于较理想的公交线网结构,对公交出行需求进行连续化的近似处理并对模型变量简化,使得模型输入参数较易获取,优化结果较易计算,为解决城市范围的偏宏观公交线网设计问题提供了新的思路与方法. 该理论体系从产生到发展都具备很强的现实背景,自提出后被不断的丰富完善并被迅速的投入到实际的应用中,取得了较好的效果. 通过实践检验,该理论体系对高性能的公交网络,如BRT系统和公交快线网等的设计更为适用,研究结果显示所设计的公交线网能够显著的降低企业与乘客的出行成本,提高整个线网的运行效率. 由于该理论体系尚处于不断丰富完善的阶段,因此在很多方面仍存在着局限性:例如出行需求均匀化的处理尚属较理想化,线网结构设定较为简单,对面向更复杂城市布局形态的线网设计仍不适用等. 因此,以下五方面关键的问题仍值得在未来进一步研究与拓展.
1) 根据更多的城市布局形态,提出相应的公交线网结构设计,包括更丰富的形态及组合方案. 对于不规则的城市布局形态,也可进行探索.
2) 研究更多样的公交出行需求形式,包括不同区域需求的差异性、公交出行需求随时间和空间变化、非均匀分布等.
3) 将分层级的线网设计理念充分融入研究中,在不同的区域布设不同等级、形态及服务水平的公交线网,满足更加多样化的公交出行需求.
4) 将更多的灵活布线策略加入到研究体系中,考虑更多的影响因素,并优化相应算法.
5) 在更多城市进行案例分析,探究该理论体系更为广泛的实际应用价值.
| [1] |
CEDER A, WILSON N H. Bus network design[J].
Transportation Research Part B: Methodological,1986, 20 (4) : 331-344.
DOI: 10.1016/0191-2615(86)90047-0 ( 0) 0)
|
| [2] |
BAGLOEE S A, CEDER A. Transit-network design methodology for actual-size road networks[J].
Transportation Research Part B: Methodological,2011, 45 (10) : 1787-1804.
DOI: 10.1016/j.trb.2011.07.005 ( 0) 0)
|
| [3] |
OUYANG Y, NOURBAKHSH S M, CASSIDY M J. Continuum approximation approach to bus network design under spatially heterogeneous demand[J].
Transportation Research Part B: Methodological,2014, 68 : 333-344.
DOI: 10.1016/j.trb.2014.05.018 ( 0) 0)
|
| [4] |
GUIHAIRE V, HAO J K. Transit network design and scheduling: a global review[J].
Transportation Research Part A: Policy and Practice,2008, 42 (10) : 1251-1273.
DOI: 10.1016/j.tra.2008.03.011 ( 0) 0)
|
| [5] |
CEDER A. Operational objective functions in designing public transport routes[J].
Journal of Advanced Transportation,2001, 35 (2) : 125-144.
DOI: 10.1002/atr.5670350205 ( 0) 0)
|
| [6] |
FAN W, MACHEMEHL R B. Optimal transit route network design problem with variable transit demand: genetic algorithm approach[J].
Journal of Transportation Engineering,2006, 132 (1) : 40-51.
DOI: 10.1061/(ASCE)0733-947X(2006)132:1(40) ( 0) 0)
|
| [7] |
KEPAPTSOGLOU K, KARLAFTIS M. Transit route network design problem: review[J].
Journal of Transportation Engineering,2009, 135 (8) : 491-505.
DOI: 10.1061/(ASCE)0733-947X(2009)135:8(491) ( 0) 0)
|
| [8] |
MANDL C E. Evaluation and optimization of urban public transportation networks[J].
European Journal of Operational Research,1980, 5 (6) : 396-404.
DOI: 10.1016/0377-2217(80)90126-5 ( 0) 0)
|
| [9] |
VAN NES R, BOVY P. The importance of objectives in urban transit network design[J].
Transportation Research Record,2000, 1735 : 50-57.
DOI: 10.3141/1735-04 ( 0) 0)
|
| [10] |
DELLE SITE P, FILIPPI F. Bus service optimization with fuel saving objective and various financial constraints[J].
Transportation Research Part A: Policy and Practice,2001, 35 (2) : 157-176.
DOI: 10.1016/S0965-8564(99)00053-1 ( 0) 0)
|
| [11] |
BELTRAN B, CARRESE S, CIPRIANI E, et al. Transit network design with allocation of green vehicles: a genetic algorithm approach[J].
Transportation Research Part C: Emerging Technologies,2009, 17 (5) : 475-483.
DOI: 10.1016/j.trc.2009.04.008 ( 0) 0)
|
| [12] |
FUSCO G, ALESSANDRINI A, COLOMBARONI C, et al. A model for transit design with choice of electric charging system[J].
Procedia-Social and Behavioral Sciences,2013, 87 : 234-249.
DOI: 10.1016/j.sbspro.2013.10.607 ( 0) 0)
|
| [13] |
JOVANOVIĆ A D, PAMUČAR D S, PEJČIĆ-TARLE S. Green vehicle routing in urban zones-a neuro-fuzzy approach[J].
Expert systems with applications,2014, 41 (7) : 3189-3203.
DOI: 10.1016/j.eswa.2013.11.015 ( 0) 0)
|
| [14] |
KOCUR G, HENDRICKSON C. Design of local bus service with demand equilibration[J].
Transportation Science,1982, 16 (2) : 149-170.
DOI: 10.1287/trsc.16.2.149 ( 0) 0)
|
| [15] |
VAUGHAN R. Optimum polar networks for an urban bus system with a many-to-many travel demand[J].
Transportation Research Part B: Methodological,1986, 20 (3) : 215-224.
DOI: 10.1016/0191-2615(86)90018-4 ( 0) 0)
|
| [16] |
CHANG S K, SCHONFELD P M. Multiple period optimization of bus transit systems[J].
Transportation Research Part B: Methodological,1991, 25 (6) : 453-478.
DOI: 10.1016/0191-2615(91)90038-K ( 0) 0)
|
| [17] |
CHANG S K, SCHONFELD P M. Welfare maximization with financial constraints for bus transit systems[J].
Transportation Research Record,1993, 1395 : 48-57.
( 0) 0)
|
| [18] |
杨哗, 许炎, 曹国华. 香港大公交系统概况及对内地城市公交系统的启示[J].
江苏城市规划,2006 (11) : 16-20.
YANG Hua, XU Yan, CAO Guohua. Overview of the bus system in Hong Kong and experience to mainland urban bus system[J]. Jiangsu Urban Planning,2006 (11) : 16-20. (  0) 0)
|
| [19] |
CHIEN S I J, SPASOVIC L N. Optimization of grid bus transit systems with elastic demand[J].
Journal of Advanced Transportation,2002, 36 (1) : 63-91.
DOI: 10.1002/atr.5670360105 ( 0) 0)
|
| [20] |
LEE Y J, VUCHIC V R. Transit network design with variable demand[J].
Journal of Transportation Engineering,2005, 131 (1) : 1-10.
DOI: 10.1061/(ASCE)0733-947X(2005)131:1(1) ( 0) 0)
|
| [21] |
QUADRIFOGLIO L, DESSOUKY M M, PALMER K. An insertion heuristic for scheduling mobility allowance shuttle transit (MAST) services[J].
Journal of Scheduling,2007, 10 (1) : 25-40.
DOI: 10.1007/s10951-006-0324-6 ( 0) 0)
|
| [22] |
张玉琇. 深圳市小支线巴士服务模式研究[D]. 成都: 西南交通大学,2014.
ZHANG Yuxiu. Research of the small feeder bus service mode in Shenzhen[D]. Chengdu: Southwest Jiaotong University, 2014. (  0) 0)
|
| [23] |
KUAH G K, PERL J. The feeder-bus network-design problem[J].
Journal of the Operational Research Society,1989, 40 (8) : 751-767.
DOI: 10.2307/2583682 ( 0) 0)
|
| [24] |
BAAJ M H, MAHMASSANI H S. Hybrid route generation heuristic algorithm for the design of transit networks[J].
Transportation Research Part C: Emerging Technologies,1995, 3 (1) : 31-50.
DOI: 10.1016/0968-090X(94)00011-S ( 0) 0)
|
| [25] |
CHIEN S, YANG Z, HOU E. Genetic algorithm approach for transit route planning and design[J].
Journal of Transportation Engineering,2001, 127 (3) : 200-207.
DOI: 10.1061/(ASCE)0733-947X(2001)127:3(200) ( 0) 0)
|
| [26] |
WU J, SONG R, WANG Y, et al. Modeling the coordinated operation between bus rapid transit and bus[J].
Mathematical Problems in Engineering,2015, 2015 : 7.
DOI: 10.1155/2015/709389 ( 0) 0)
|
| [27] |
SHRIVASTAVA P, O’MAHONY M. Design of feeder route network using combined genetic algorithm and specialized repair heuristic[J].
Journal of Public Transportation,2007, 10 (2) : 99-123.
( 0) 0)
|
| [28] |
SHRIVASTAVA P, O’MAHONY M. Modeling an integrated public transportation system a case study in Dublin, Ireland[J].
European Transport,2009, 41 : 28-46.
( 0) 0)
|
| [29] |
SZETO W Y, WU Y. A simultaneous bus route design and frequency setting problem for Tin Shui Wai, Hong Kong[J].
European Journal of Operational Research,2011, 209 (2) : 141-155.
DOI: 10.1016/j.ejor.2010.08.020 ( 0) 0)
|
| [30] |
ZHAO F, ZENG X. Simulated annealing-genetic algorithm for transit network optimization[J].
Journal of Computing in Civil Engineering,2006, 20 (1) : 57-68.
DOI: 10.1061/(ASCE)0887-3801(2006)20:1(57),57-68 ( 0) 0)
|
| [31] |
FARAHANI R Z, MIANDOABCHI E, SZETO W Y, et al. A review of urban transportation network design problems[J].
European Journal of Operational Research,2013, 229 (2) : 281-302.
DOI: 10.1016/j.ejor.2013.01.001 ( 0) 0)
|
| [32] |
MA Y, LI J, HAN C P. A planning tool for maximising transit services[J].
Transportmetrica B: Transport Dynamics,2015, 4 (1) : 1-22.
DOI: 10.1080/21680566.2015.1017023Yunfeng ( 0) 0)
|
| [33] |
YU B, YANG Z Z, JIN P H, et al. Transit route network design-maximizing direct and transfer demand density[J].
Transportation Research Part C: Emerging Technologies,2012, 22 : 58-75.
DOI: 10.1016/j.trc.2011.12.003 ( 0) 0)
|
| [34] |
CURTIN K M, BIBA S. The transit route arc-node service maximization problem[J].
European Journal of Operational Research,2011, 208 (1) : 46-56.
DOI: 10.1016/j.ejor.2010.07.026 ( 0) 0)
|
| [35] |
SZETO W Y, JIANG Y. Hybrid artificial bee colony algorithm for transit network design[J].
Transportation Research Record: Journal of the Transportation Research Board,2012, 2284 : 47-56.
DOI: 10.3141/2284-06 ( 0) 0)
|
| [36] |
NAYEEM M A, RAHMAN M K, RAHMAN M S. Transit network design by genetic algorithm with elitism[J].
Transportation Research Part C: Emerging Technologies,2014, 46 : 30-45.
DOI: 10.1016/j.trc.2014.05.002 ( 0) 0)
|
| [37] |
WANG J Y, LIN C M. Mass transit route network design using genetic algorithm[J].
Journal of the Chinese Institute of Engineers,2010, 33 (2) : 301-315.
DOI: 10.1080/02533839.2010.9671619 ( 0) 0)
|
| [38] |
DICKINSON R E.
The west European city: a geographical interpretation[M]. London: Routledge and Kegan Paul, 1963 .
( 0) 0)
|
| [39] |
LYNCH K, HACK G.
Site planning[M]. Cambridge: MIT Press, 1971 .
( 0) 0)
|
| [40] |
BLACK A. Optimizing urban mass transit systems: a general model[J].
Transportation Research Record: Journal of the Transportation Research Board,1978, 677 : 41-47.
( 0) 0)
|
| [41] |
TSAO S, SCHONFELD P. Optimization of zonal transit service[J].
Journal of Transportation Engineering,1983, 109 (2) : 257-272.
DOI: 10.1061/(ASCE)0733-947X(1983)109:2(257) ( 0) 0)
|
| [42] |
DAGANZO C F. Structure of competitive transit networks[J].
Transportation Research Part B: Methodological,2010, 44 (4) : 434-446.
DOI: 10.1016/j.trb.2009.11.001 ( 0) 0)
|
| [43] |
TIRACHINI A, HENSHER D A, JARA-DAZ S R. Comparing operator and users costs of light rail, heavy rail and bus rapid transit over a radial public transport network[J].
Research in Transportation Economics,2010, 29 (1) : 231-242.
DOI: 10.1016/j.retrec.2010.07.029 ( 0) 0)
|
| [44] |
ESTRADA M, ROCA-RIU M, BADIA H, et al. Design and implementation of efficient transit networks: procedure, case study and validity test[J].
Transportation Research Part A: Policy and Practice,2011, 45 (9) : 935-950.
DOI: 10.1016/j.tra.2011.04.006 ( 0) 0)
|
| [45] |
BADIA H, ESTRADA M, ROBUST F. Competitive transit network design in cities with radial street patterns[J].
Transportation Research Part B: Methodological,2014, 59 : 161-181.
DOI: 10.1016/j.trb.2013.11.006 ( 0) 0)
|
| [46] |
CHEN H, GU W, CASSIDY M J, et al. Optimal transit service atop ring-radial and grid street networks: a continuum approximation design method and comparisons[J].
Transportation Research Part B: Methodological,2015, 81 : 755-774.
DOI: 10.1016/j.trb.2015.06.012 ( 0) 0)
|
| [47] |
NOURBAKHSH S M, OUYANG Y. A structured flexible transit system for low demand areas[J].
Transportation Research Part B: Methodological,2012, 46 (1) : 204-216.
DOI: 10.1016/j.trb.2011.07.014 ( 0) 0)
|
| [48] |
王振报, 陈艳艳. 方格型城市多模式公交线网关键设计参数优化[J].
交通运输系统工程与信息,2014, 14 (6) : 176-181.
DOI: 10.3969/j.issn.1009-6744.2014.06.028 WANG Zhenbao, CHEN Yanyan. Optimization for key design parameters of multi-modal public transport network on grid urban structure[J]. Journal of Transportation Systems Engineering and Information Technology,2014, 14 (6) : 176-181. DOI: 10.3969/j.issn.1009-6744.2014.06.028 (  0) 0)
|
| [49] |
CIPRIANI E, GORI S, PETRELLI M. A bus network design procedure with elastic demand for large urban areas[J].
Public Transport,2012, 4 (1) : 57-76.
DOI: 10.1007/s12469-012-0051-7 ( 0) 0)
|
| [50] |
MIRHASSANI S A, NAMAZI A, NAMAZI V. Designing an efficient transit network for large cities[J].
International Journal of Management Science and Engineering Management,2014, 9 (4) : 286-298.
DOI: 10.1080/17509653.2014.903811 ( 0) 0)
|
| [51] |
TRAPOTE-BARREIRA C, ROBUST F, BADIA H, et al. Learnings From urban bus network change[C]// 95th Annual Meeting of Transportation Research Board. Washington DC: Transportation Research Board, 2016:16-6772.
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


