路网容量由于道路施工、交通事故或者天气等原因会随机波动,使得出行者的行程时间随机变化,从而导致行程时间可靠性也随机变化. 行程时间和行程时间可靠性是出行者路径选择的主要因素,但是出行者有时也会将货币费用考虑进来. 经验研究表明行程时间、行程时间可靠性以及货币费用是影响出行者路径选择标准的3个最重要的因素[1]. 关于这3个因素的研究有很多,例如刘海旭等[2]综合考虑了行程时间和行程时间可靠性,建立了基于行程质量的随机用户平衡模型;冷军强等[3]定义冰雪条件下的广义出行费用为出行者的行程时间和行程时间可靠性及出行安全性的加权综合. 胡文君等[4]按照出行时间和出行费用两个准则建立了广义出行阻抗的多用户多模式多准则的随机用户网络均衡模型. 以上均是其中两个因素的运用,把3个因素全部考虑的研究很少见. 由于交通网络的各种随机性和不确定性因素的影响,城市道路网络中的某路段或路径会造成通行能力下降,从而导致整体或局部路网的通行能力不同程度的降级. 以往的研究也都是在需求为随机的环境下研究,从路网降级变化的随机环境研究出行费用的较少. 韦增欣等[5]研究了弹性需求下降级路网随机用户均衡模型,但该模型中只考虑了行程时间成本,只研究了降级不同对流量的影响,没有全面考虑其他因素,分析也不够全面. 而现有的研究多是静态网络随机型用户模型,这对于现实来说过于简化,不能很好地用于实践. 鉴于此,本文将全面考虑影响出行者路径选择的3个因素,提出“动态广义出行费用”,以估计此费用最小作为路径选择准则,在弹性需求及降级路网条件下建立随机用户平衡.
1 降级路网下的时间分布设交通网络G=(N,A),N为网络中节点的集合,A为路段集合,路段a∈A,W表示起讫点OD对集合,ω∈W,Kω表示起讫点OD对ω间路径集合,路径k∈Kω. 路网上的交通需求为交通流量,交通供给为道路通行能力或称为道路容量,此两者均为随机变量,下面介绍其随机分布. 本文规定以下大写字母为随机变量,小写字母为固定变量.
路段行程时间通常采用BPR函数描述,路段a上的行程时间Ta为
| ${{T}_{a}}={{T}_{a}}({{x}_{a}},{{C}_{a}})={{t}^{0}}_{a}(1+\beta {{({{x}_{a}}/{{C}_{a}})}^{n}}).$ | (1) |
式中ta0、xa、Ca分别为路段a的自由流行程时间、实际流量、实际通行能力;β和n为确定性参数.
路段通行能力Ca为随机变量,故路段行程时间Ta也为随机变量. 本文假设Ca服从平均分布,上界为道路设计容量ca,下界为ηaca. ηa为路段a通行能力最大降级系数,即Ca~U(ηaca,ca),其中0 <ηa≤1. ηa=1为理想情况,本文不考虑此情况. n>1时,假定路段通行能力相互独立,路段行程时间的均值ta和标准差σta分别为[6-7]
| ${{t}_{a}}=E({{T}_{a}})=t_{a}^{0}+\beta t_{a}^{0}\frac{1-{{({{{\bar{\eta }}}_{a}})}^{1-n}}}{{{({{c}_{a}})}^{n}}(1-{{{\bar{\eta }}}_{a}})\left( 1-n \right)}{{({{x}_{a}})}^{n}}.$ | (2) |
| $\begin{align} & var({{T}_{a}})={{\beta }^{2}}{{(t_{a}^{0})}^{2}}\frac{1}{{{({{{\bar{c}}}_{a}})}^{2n}}}{{({{x}_{a}})}^{2n}}\cdot \\ & \left\{ \frac{1-{{({{{\bar{\eta }}}_{a}})}^{1-2n}}}{(1-{{{\bar{\eta }}}_{a}})\left( 1-2n \right)}-{{\left[ \frac{1-{{({{{\bar{\eta }}}_{a}})}^{1-n}}}{(1-{{{\bar{\eta }}}_{a}})\left( 1-n \right)} \right]}^{2}}~ \right\}, \\ \end{align}$ | (3) |
| $\begin{align} & \sigma _{t}^{a}=\sqrt{var({{T}_{a}})}=\beta t_{a}^{0}\frac{1}{{{({{{\bar{c}}}_{a}})}^{n}}}{{({{x}_{a}})}^{n}}\cdot \\ & \sqrt{\left\{ \frac{1-{{({{{\bar{\eta }}}_{a}})}^{1-2n}}}{(1-{{{\bar{\eta }}}_{a}})\left( 1-2n \right)}-{{\left[ \frac{1-{{({{{\bar{\eta }}}_{a}})}^{1-n}}}{(1-{{{\bar{\eta }}}_{a}})\left( 1-n \right)} \right]}^{2}} \right\}}. \\ \end{align}$ | (4) |
由上面假设可知路段行程时间也是独立的,故ω间有效路径的出行时间就是与该路径相关联的所有路段的行程时间和,可以表示为
| $T_{k}^{\omega }=\sum\limits_{a\in A}{\delta _{k,a}^{\omega }}{{T}_{a}},\forall k\in {{K}_{\omega }},\omega \in W.$ | (5) |
式中:δk,aω为路段-路径关联系数,如果路段a在路径k上,δk,aω=1;否则为0.
根据中心极限定理,不论路段行程时间分布如何,路径行程时间均服从正态分布Tkω~N(E(Tkω),(σkω)2),路径行程时间均值tkω和标准差σkω分别为
| $t_{k}^{\omega }=E(T_{k}^{\omega })=\sum\limits_{a\in A}{\delta _{k,a}^{\omega }}{{t}_{a}},\forall k\in {{K}_{\omega }},\omega \in W;$ | (6) |
| $\sigma _{k}^{\omega }=\sqrt{\sum\limits_{a\in A}{\delta _{k,a}^{\omega }}{{(\sigma _{t}^{a})}^{2}}},\forall k\in {{K}_{\omega }},\omega \in W.$ | (7) |
降级路网上的路段行程时间由式(1)可转变为
| ${{T}_{a}}=t_{a}^{0}\{1+\beta {{[{{x}_{a}}/({{\eta }_{a}}{{{\bar{c}}}_{a}})]}^{n}}\}.$ | (8) |
式中ηa为路段a受到外界因素影响后的通行能力的实际降级参数. 该系数越大,说明实际通行能力越大. 一般有ηa≥ηa,表示路段实际降级后的通行能力大于等于最大降级后的通行能力. 上式表明路段行程时间与路段实际流量以及实际降级系数有关,随着流量和降级系数的变化而变化.
Asakura等[8]首次提出行程时间可靠性的概念,该指标可以反映行程时间波动性. 行程时间可靠性是指在一定条件下,出行者所用实际行程时间小于等于规定时间阈值的概率. 路段或路径行程时间可靠性R可以表示为
| $R=P\left\{ X\le Y \right\}.$ | (9) |
式中:P为概率计算;X为实际行程时间;Y为规定的时间阈值.
假设路段行程时间也服从正态分布,则路段或路径的行程时间可靠性又可以进一步表示为[9]
| $R=\Phi \left[ \frac{Y-{{\mu }_{X}}}{{{\sigma }_{X}}} \right].$ | (10) |
式中:Φ(·)为标准正态分布函数;μX、σX分别为路段或路径的行程时间均值和标准差,都是与流量相关的函数,故R也是与流量相关的函数,随着实际流量的变化而变化.
2.2 动态广义出行费用出行者除了考虑行程时间以及其波动外,还会考虑出行中的一些货币支出. 总的出行费用不仅包括出行者的行程时间机会成本和行程时间不可靠负效用所产生的费用,也包括道路上因维护、油耗等产生的各种货币费用支出. 出行者在降级路网条件下最理想的目标是选择行程时间最小,行程时间可靠性最高,并且货币费用最少的路径作为出行依据,但是这3个目标间难免有冲突,相互矛盾,不能同时满足. 例如要减少行程时间,往往需要经过一些收费路段;又如要提高行程时间可靠性,必须走行程时间较高的路径,或者还要支付一定的货币费用. 出行者需要在这3个目标中寻求一个折中方案,因此可定义这三者的加权综合,用广义出行费用来描述. 路段a的广义出行费用ma可表示为
| ${{m}_{a}}={{\omega }_{1}}\varphi {{T}_{a}}+{{\omega }_{2}}\tau (1-{{R}_{a}})+{{\omega }_{3}}{{\lambda }_{a}}.$ | (11) |
式中:Ta为路段a的行程时间;Ra为路段a的行程时间可靠性;λa为路段a上的货币费用;φ为时间价值系数,可以将时间转换为费用;τ为行程时间可靠性价值系数,可以将不可靠负效用转化为费用; τ/φ为可靠性比率,可靠性价值一般大于时间价值[10],所以τ/φ>1; ω1φTa为时间机会成本费用; ω2τ(1-Ra)为不可靠负效用费用; ω3λa为货币费用,ω1、ω2、ω3这3个权重系数反映了出行者对待风险的态度,ω1+ω2+ω3=1;ω1越大,说明出行者偏好以行程时间作为路径选择标准;ω2越大,说明出行者为风险规避型,趋向于以行程时间可靠性为路径选择标准;ω3越大,说明出行者趋向于以出行货币费用为路径选择准则.
OD对ω间路径k的广义出行费用mkω为
| $\begin{align} & m_{k}^{\omega }=\sum\limits_{a\in A}{\delta _{k,a}^{\omega }{{m}_{a}}}={{\omega }_{1}}\varphi \sum\limits_{a\in A}{\delta _{k,a}^{\omega }{{T}_{a}}}+ \\ & {{\omega }_{2}}\tau \sum\limits_{a\in A}{\delta _{k,a}^{\omega }}(1-{{R}_{a}})+{{\omega }_{3}}\sum\limits_{a\in A}{\delta _{k,a}^{\omega }{{\lambda }_{a}}}. \\ \end{align}$ | (12) |
因路段流量的变化,各路段或路径的行程时间和行程时间可靠性都会随之而变化,故广义出行费用并非静态不变,而是动态变化的,所以用“动态广义出行费用”可以更贴切描述这一概念. 因为Ta为xa的严格单调递增函数,1-Ra为严格单调递增函数,所以路段和路径动态广义出行费用均为流量的严格单调递增函数.
3 广义出行费用随机用户平衡模型 3.1 随机用户平衡条件在实际出行中,出行者对路网状况不可能完全了解,因此出行者估计的路径广义出行费用是一个随机变量. 假定出行者以估计广义出行费用最小为路径选择准则,对于某一出行者,每条路径均有一个被选择的概率. 假设估计广义出行费用与实际广义出行费用存在一个随机误差,相互独立并服从Gumbel分布. 根据离散模型理论[11],OD对ω间的路径k被选择的概率Pkω为
| $P_{k}^{\omega }=\frac{\partial E\left[ \underset{k\in {{K}_{\omega }}}{\mathop{min}}\,M_{k}^{\omega }|{{m}^{\omega }} \right]}{\partial m_{k}^{\omega }}.$ | (13) |
式中Mkω、mkω分别为OD对ω间的路径k的估计广义出行费用和实际广义出行费用; mω为mkω的向量表示. 上式还可以表示为
| $P_{k}^{\omega }=exp(-\theta m_{k}^{\omega })/\sum\limits_{r\in {{K}_{\omega }}}{exp}(-\theta {{m}^{\omega }}_{r}).$ | (14) |
式中θ为出行者对路径的熟悉程度,θ越大表示出行者对路况越熟悉.
出行者的路径选择最终将达到Logit随机用户平衡,即任何一个出行者都不可能通过单方面改变出行路径来减少自己的估计广义出行费用,但某个OD对间所有已被选用的路径上,并不一定有相同的实际广义出行费用,而只满足
| $f_{k}^{\omega }={{q}_{\omega }}P_{k}^{\omega },\forall k,\omega .$ | (15) |
式中fkω为OD对ω间路径k上的交通量;qω为OD对ω间的交通量.
假定出行者的OD交通量qω是关于OD对ω间期望最小出行费用Sω的严格单调递减函数,用Dω(·)表示,并且具有上限qω,则可表示为
| ${{q}_{\omega }}={{D}_{\omega }}({{S}_{\omega }})\le {{{\bar{q}}}_{\omega }}.$ | (16) |
用Dω-1(·)表示OD交通量反函数,则期望最小出行费用Sω可表示为
| $\begin{align} & {{S}_{\omega }}=D_{\omega }^{-1}({{q}_{\omega }})=E\left[ \underset{k\in {{K}_{\omega }}}{\mathop{min}}\,M_{k}^{\omega }|{{m}^{\omega }} \right]= \\ & -\frac{1}{\theta }ln\sum\limits_{r\in {{K}_{\omega }}}{exp}(-\theta {{m}^{\omega }}_{k}). \\ \end{align}$ | (17) |
可采用下面的数学规划模型:
| $\begin{align} & minZ\left( x,f,q \right)=\frac{1}{\theta }\sum\limits_{\omega \in W}{\sum\limits_{k\in {{K}_{\omega }}}{f_{k}^{\omega }lnf_{k}^{\omega }}}\text{ }-\frac{1}{\theta }\sum\limits_{\omega \in W}{{{q}_{\omega }}ln~{{q}_{\omega }}}+ \\ & \sum\limits_{a\in A}{\int_{0}^{{{x}_{a}}}{{{m}_{a}}}}\left( \omega \right)d\omega -\sum\limits_{\omega \in W}{\int_{0}^{{{q}_{\omega }}}{D_{\omega }^{-1}}}\left( \omega \right)d\omega . \\ \end{align}$ | (18) |
| $\begin{matrix} s.t. & \sum\limits_{k\in {{K}_{\omega }}}{f_{k}^{\omega }}={{q}_{\omega }},\forall \omega \in W; \\ \end{matrix}$ | (19) |
| ${{x}_{a}}=\sum\limits_{\omega \in W}{\sum\limits_{k\in {{K}_{\omega }}}{f_{k}^{\omega }}}\delta _{k,a}^{\omega },\forall a\in A;$ | (20) |
| $f_{k}^{\omega }\ge 0,{{q}_{\omega }}\ge 0,\forall k\in {{K}_{\omega }},\forall \omega \in W.$ | (21) |
式(18)为目标函数;式(19)、(20)分别为路径流量和路段流量守恒约束条件;式(21)为流量非负约束.
由Kuhn-Tucker一阶最优性条件容易证明该模型同时满足SUE条件和需求函数,是弹性需求下的SUE模型. 又该模型中ma(ω)为路段流量的严格单调递增函数,所以目标函数是关于流量的严格凸函数. 模型的约束构成的集合为凸集,根据最优化理论,定义在凸集上的严格凸函数,其最优解唯一[12].
3.3 模型的求解算法利用MSA算法求解模型,步骤如下:1) 初始化. 基于零流计算路段广义出行费用{ma(0)=ma(0)}(∀a),计算S
图 1为算例网络,包括2个OD对(Q12,Q56)4条路径和7条路段. 令参数τ=1.5φ,φ=1,θ=1;BPR函数中的参数β=0.15,n=4;规定时间阈值Y=30 min,ε=0.001. 假设OD流量为qω=qω-1.5Sω,q12=q56=50 veh·min-1. 各路段的属性见表 1.
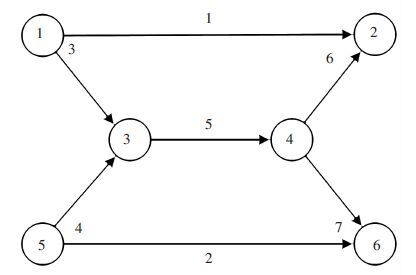
|
图 1 算例网络 Figure 1 Example network |
| 表 1 路段属性 Table 1 Section properties |
初始路网条件假定3个出行指标权重分别为ω1=0.3,ω2=0.5,ω3=0.2;7个路段的实际降级系数分别为0.9、0.9、0.6、0.7、0.9、0.6、0.7; 7个路段的货币费用分别为16、10、0、3、0、0、5. 根据这些参数设置,可得到平衡配流结果. 平衡时路段上的流量x1=29.742 4,x2=27.181 5,x3=10.405 4,x4=12.622 3,x5=23.027 7,x6=10.405 4,x7=12.622 3. 循环次数l=6. 平衡时的各路径流量pi及广义出行费用mi见表 2.
| 表 2 路径平衡配流结果 Table 2 Equilibrium assignment results of path |
从平衡配流结果可知,在设定的初始路网条件下,因为路径1和路径4具有较小的自由流行程时间和较大的实际通行能力,虽然货币费用较高,但考虑到多数出行者受此费用影响较小而设定较小的权重,因此具有较低的广义出行费用,故流量分配较大.
4.2 参数灵敏度分析模型中的指标权重可以体现出行者对行程时间、行程时间可靠性以及货币费用的不同风险偏好程度和选择标准;路段的实际降级系数是路段在某一假设条件下的降级程度,影响着路段的行程时间,进而会造成流量的变化,最后会导致行程时间可靠性的变化;货币费用为实际路网中的路段货币费用,本文假设是固定值,与流量等没有关系,根据经验货币费用的变化也会影响出行者出行行为. 根据本文假设,三者之间没有相关性. 故下面将对这3个参数分别取不同值进行灵敏度分析,其他参数取值与初始假定相同,通过平衡分配结果来验证出行者路径选择行为是否与经验相符.
1) 指标权重影响. 指标权重取不同值时的平衡分配结果如表 3所示.
从表 3可以看出:ω1较大时,出行者趋向于以行程时间为选择标准,因路径1的行程时间最小,故几乎分配了q12所有的流量;路径4的行程时间也较小,故分配了q56的95.3%流量. ω2较大时,出行者偏好以行程时间可靠性为选择依据,路径1、4分配流量稍大,路径2、3稍小. 这是因为出行者基于可靠性考虑时会选择路段数较少且降级后通行能力较大的路径1、4;而路径2、3降级后通行能力稍小并且路段数较多,故可靠性较小,流量较少. ω3较大时,出行者偏好以货币费用为选择标准. 路径1的费用最高,所以流量几乎为0,路径2由于费用为0,分配了几乎全部的流量;路径3上费用略小于路径4的,分配了69.4%的流量. 由此可见,3个权重系数对道路流量分配影响显著. 权重系数组合不同对应不同的分配结果,并且与经验相符.
| 表 3 不同权重的平衡分配结果 Table 3 Equilibrium assignment results with different weights |
2) 实际降级系数影响. 路段的实际降级系数取值组合假设分为表 4中的5种. 实际降级系数取不同组合时的随机平衡分配结果如表 5所示.
| 表 4 路段实际降级系数组合 Table 4 Combinations of section degradation factor |
| 表 5 不同实际降级系数组合的平衡分配结果 Table 5 Equilibrium assignment results with different combinations of degradation factor |
从表 5可知:当路段实际降级系数取组合1,即都不严重时,路径1、4的流量明显高于路径2、3的. 这是由于路径1、4的行程时间最小,可靠性也最高,即使货币费用高也不影响出行者选择该路段出行. 当取组合2时,4条路径均受降级影响流量减少,两个OD对的流量也急剧下降. 此时路径1、4仍因行程时间小且路段数较少而具有很大的可靠性,故流量分配比较大. 当取组合3仅路段1降级严重时,路径1的流量最少,只占到17.67%. 当取组合4路段1、2降级严重时,路径1、4受此影响流量最少. 当取组合5时,路径2、3、4均受降级影响流量最少. 由此可见,5种组合所表示的各种路径受实际降级系数影响情况的分配结果都是降级严重路径分配流量少,降级不严重路径分配流量多,此结果与经验相吻合.
3) 货币费用影响. 路段的货币费用取值组合见表 6,不同组合对应的平衡分配结果见表 7.
| 表 6 路段货币费用组合 Table 6 Combinations of section monetary cost |
| 表 7 不同货币费用组合的平衡分配结果 Table 7 Equilibrium assignment results with different combinations of monetary cost |
从表 7可以观察到:与组合0初始参数分配结果相比:当组合1所有路段货币费用均增大时,路径2、3由于费用增加较多,使得流量分别转向路径1、4;当取组合2路段费用大于0的均减少时,因路径2费用不变,路径3减少的费用最多,故路径2的流量减少,路径3的增加,并因为费用的整体减少使两个OD对的流量均增加;组合3时,路径2的流量向路径1转移,反之取组合4时,路径1的流量又急剧向路径2移动. 当取组合5时,路段1、2费用减少,使路径1、4流量增加,反之取组合6时,流量减少. 组合7时因路径1、3、4费用减少,故流量增加,反之取组合8时流量减少. 组合1~8所体现的1条、2条、3条、4条路径受货币费用减少或增加时的流量变化与组合0的初始分配结果对比显示:货币费用减少使得流量向该路径转移,反之货币费用增大,流量向其他路径转移,分配结果与事实相符,这充分说明货币费用对出行者的路径选择行为同样具有一定影响.
5 结 论1) 在路网随机降级及需求为弹性的环境下,全面考虑了路网上影响出行者路径选择行为的3大重要指标:行程时间、行程时间可靠性和货币费用.
2) 构造了这3个指标的动态广义出行费用的随机用户平衡模型,并设计了求解算法. 算例数值结果与所设定的参数有关,但不同参数取值对应的数值结果的变化与日常经验或事实相吻合,这足以证明所建模型的有效性以及算法的正确性. 同时也验证了出行者对待风险的不同态度、实际降级系数和货币费用对出行者的路径选择行为具有显著的影响.
3) 需要进一步研究的是将规定的时间阈值和货币费用均考虑为流量或时间分布的动态函数,研究更广泛的广义出行费用的动态随机平衡分配模型;还可以研究多类型出行者建立多用户随机均衡模型.
| [1] |
WANG J Y T, EHRGOTT M, CHEN A. A bi-objective user equilibrium model of travel time reliability in a road network[J].
Transportation Research Part B,2014, 66 (8) : 4-15.
( 0) 0)
|
| [2] |
刘海旭, 蒲云. 基于行程质量的随机用户平衡分配模型[J].
中国公路学报,2004, 17 (4) : 93-95.
LIU H X, PU Y. Stochastic user equilibrium assignment model based on travel trait[J]. China Journal of Highway and Transport,2004, 17 (4) : 93-95. (  0) 0)
|
| [3] |
冷军强, 冯雨芹, 张亚平, 等. 广义出行费用下的冰雪条件路网容量可靠性[J].
哈尔滨工业大学学报,2011, 43 (2) : 92-97.
LENG J Q, FENG Y Q, ZHANG Y P, et al. Road network capacity reliability based on generalized travel cost under ice and snowfall conditions[J]. Journal of Harbin Institute of Technology,2011, 43 (2) : 92-97. (  0) 0)
|
| [4] |
胡文君, 周溪召. 多用户多模式多准则随机用户均衡模型[J].
武汉理工大学学报(交通科学与工程版),2012, 36 (2) : 366-369.
HU W J, ZHOU X Z. Amulti-user multi-mode multi-criteria stochastic user equilibrium model[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering),2012, 36 (2) : 366-369. (  0) 0)
|
| [5] |
韦增欣, 石婷, 高苏銮. 弹性需求下降级路网随机用户均衡模型及算法[J].
统计与决策,2012 (7) : 79-81.
WEI Zengxin, SHI Ting, GAO Suluan. Stochastic user equilibrium model and algorithm of degraded road network with elastic demand[J]. Statistics and Decision,2012 (7) : 79-81. (  0) 0)
|
| [6] |
LO H K, LUO X W, SIU B W Y. Degradable transport network: travel time budget of travelers with heterogeneous risk aversion[J].
Transportation Research Part B,2006, 40 (9) : 792-806.
DOI: 10.1016/j.trb.2005.10.003 ( 0) 0)
|
| [7] |
LO H K, TUNG Y K. Network with degradable links: capacity analysis and design[J].
Transportation Research Part B,2003, 37 (4) : 345-363.
DOI: 10.1016/S0191-2615(02)00017-6 ( 0) 0)
|
| [8] |
ASAKURA Y, KASHIWADANI M. Road network reliability caused by daily fluctuation of traffic flow [C] //Proceedings of the 19th PTRC Summer Annual Meeting. Victoria :ARRB Group Limited,1991: 73-84.
( 0) 0)
|
| [9] |
况爱武, 黄中祥, 况群. 随机需求道路网络出行时间可靠性评估方法[J].
西南交通大学学报,2011, 46 (5) : 861-867.
KUANG A W, HUANG Z X, KUANG Q. Evaluation method for travel time reliability of road network with stochastic demand[J]. Journal of Southwest Jiaotong University,2011, 46 (5) : 861-867. (  0) 0)
|
| [10] |
LAM T C, SMALL K A. The value of time and reliability: measurement from a value pricing experiment[J].
Transportation Research Part E,2001, 37 (2) : 231-251.
( 0) 0)
|
| [11] |
BEN-AKIVA M, LERMAN S R.
Discrete choice analysis: theory and application to travel demand[M]. Cambridge: MIT Press, 1985 : 100 -129.
( 0) 0)
|
| [12] |
SHEFFI Y.
Urban transportation networks: equilibrium analysis with mathematical programming methods[M]. New Jersey: Prentice-Hall, 1985 : 262 -342.
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


