由于液压驱动系统在输出力矩、功率密度、控制精度等方面的优势,近年来液压足式机器人成为了研究热点.2005年,美国波士顿动力公司研制成功的“BigDog”系列机器人[1]展示出了极强的运动和负载能力,因此成为各国学者争相研究和效仿的目标[2].因具备结构简单、工作空间小等优点,上述液压机器人均选择非对称液压缸作为关节运动驱动器.但非对称缸的两腔活塞面积不同,在作伸出和缩回运动时相关参数会发生变化,使动态性能出现较大差异,加大了液压驱动系统的非线性度.这种不良现象还会伴随机器人运动状态和自身负重等因素的改变而加剧,严重影响机器人的运动灵活性和稳定性.很多学者对非对称缸系统进行过线性或非线性建模研究,并试图在此基础上寻找能解决上述问题的控制算法.其中,模糊控制以更接近人类思维的处理方式,引起了广泛的关注.文献[3]使用模糊控制器实现了对数字泵控液压缸的位置控制,达到了节能降耗的目的.文献[4]利用模糊控制对比例阀的死区进行补偿,消除了液压缸运动的不对称现象.文献[5]基于模糊理论提出了模型参考变增益自适应控制算法,实现了非对称液压缸的对称性控制.以上基于模糊算法的研究为改善非对称缸的控制提供了有益的尝试.
自适应模糊PID是一种基于模糊理论的控制算法,它将模糊推理系统与常规PID控制相结合,发挥两者的优势.该算法可根据实际工况对PID参数不断进行模糊化增量调节,使控制器具备处理非线性和参数时变系统的能力,在不需要精确数学模型的前提下,使被控对象具有更好的静、动态性能[6].本文结合研制的“Hound”液压四足机器人,设计了适合用于非对称液压缸动态控制的自适应模糊PID算法控制器,用于驱动机器人腿关节运动以实现良好的足端轨迹跟踪.
1 液压驱动系统分析Hound四足机器人的运动学结构(见图 1)源于猎犬的骨骼系统,其腿部结构由大腿、小腿和足等部分组成,包括3个主动关节—侧摆关节、髋关节和膝关节.

|
图 1 Hound机器人机体结构 Figure 1 The body structure of Hound robot |
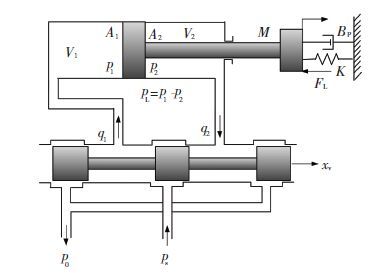
腿部主动关节均由对称阀控非对称液压缸系统(以下简称为“阀控缸系统”)驱动,其结构原理如图 2所示[7-8].
|
图 2 阀控缸系统原理 Figure 2 The schematic diagram of valve-controlled cylinder system |
图中,M为负载质量,xv为阀芯位移,y为活塞杆位移,Bp为负载粘性阻力系数,K为弹性系数,FL为外部负载(干扰)力,ps为供油压力,p0为回油压力,p1为无杆腔压力,p2为有杆腔压力,q1为无杆腔流量,q2为有杆腔流量,A1、A2分别为无杆腔、有杆腔活塞作用面积.
根据图 2可以得到描述阀控缸系统动态性能的3个基本方程,进行拉普拉斯变换,阀的流量方程、液压缸的流量连续方程以及力平衡方程分别为
| ${{q}_{L}}={{K}_{q}}{{x}_{v}}-{{K}_{c}}{{p}_{L}},$ | (1) |
| ${{q}_{L}}={{q}_{1}}={{C}_{ie}}{{p}_{L}}+{{C}_{f}}{{p}_{s}}+\frac{{{V}_{t}}}{4{{\beta }_{e}}}s{{p}_{L}}+{{A}_{1}}sy,$ | (2) |
| $F={{p}_{L}}{{A}_{1}}={{M}_{t}}{{s}^{2}}y+{{B}_{p}}sy+Ky+{{F}_{L}}$ | (3) |
式中:qL为负载流量,pL为负载流量,Vt为液压缸容积,βe为液压油弹性模量,Kq为阀口流量增益,Kc为流量-压力系数,Cie为等效泄漏系数,Cf为额外流量系数.
将式(1)~(3)叠加在一起并忽略某些数值较小的项,可得到当伺服阀阀芯右移(xv>0)时(此时液压缸活塞杆伸出),液压阀驱动电路的输入电压U和系统外负载力FL同时作用时的非对称阀控缸系统数学模型为
| $Y(s)=\frac{{{K}_{a}}{{K}_{v}}}{{{A}_{1}}}U(s)-\frac{\frac{{{K}_{ce}}}{A_{1}^{2}}(\frac{{{V}_{t}}}{4{{\beta }_{e}}{{K}_{ce}}}s+1){{F}_{L}}\left( s \right)}{s(\frac{{{s}^{2}}}{\omega _{n}^{2}}+\frac{2{{\xi }_{n}}}{{{\omega }_{n}}}s+1)}.$ | (4) |
式中:Kce为阀总流量-压力系数(Kc+Cf);Kv为阀流量增益(Kv= KqKsv);Ksv为阀芯位移增益;Ka为驱动电路增益;ωn为系统固有频率,
当伺服阀阀芯左移(xv < 0)时(此时液压缸活塞杆缩回),此时阀控缸系统的数学模型的形式与式(4)相同,但式中的各项增益系数会因活塞作用面积不同而有所变化,ωn、ξn等项数值也会随之变化(具体变化见文献[9-10]),同时还会导致两腔压力p1、p2在换向时发生突跳. 另外,在机器人运行时不同的负载重量、动作幅度、关节角位移以及不可预测的外来干扰,会实时改变驱动液压缸受力的大小和方向.以上因素均会导致阀控缸系统在不同方向的动作时产生非线性现象和参数变化,影响驱动关节的运动平稳度,加大控制难度,因此常规的PID控制(固定参数)已经无法应对.为了提高系统的控制性能,满足机器人平稳运行的要求,设计了自适应模糊PID算法.
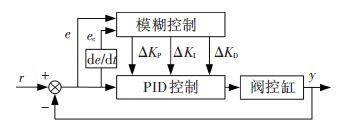
2 自适应模糊PID控制算法自适应模糊PID通过建立误差e、误差变化率ec同PID增量参数ΔKP、ΔKI、ΔKD相对应的模糊规则来实现调节作用. 该算法最大的优势是不破坏原有常规PID的控制效果,仅依据系统的跟踪误差对PID参数进行增量调节(增量可正可负)[11-12],使PID参数实时改变以应对系统的变化,因此有别于常规PID一成不变的控制参数模式,可以实现对参数时变或非线性系统的良好控制,其算法原理如图 3所示.
|
图 3 自适应模糊PID算法原理 Figure 3 The schematic diagram of self-tuning fuzzy-PID control algorithm |
将e、ec的论域均设为{6,5,4,3,2,1,0,-1,-2,-3,-4,-5,-6},ΔKP、ΔKI、ΔKD的论域均设为{3,2,1,0,-1,-2,-3},并分别被模糊化为7个级别,即{PB,PM,PS,ZO,NS,NM,NB}. 以对ΔKP的模糊调节为例,按照表 1在MATLAB的模糊工具箱里建立模糊规则表,即可得到针对ΔKP的模糊系统输入/输出特性曲面[13],如图 4所示.
| 表 1 ΔKP模糊控制规则表 Table 1 The fuzzy control rule table of ΔKP |

|
图 4 ΔKP的模糊推理特性曲面 Figure 4 The output surface of fuzzy inference system (FIS) of ΔKP |
以模糊规则表为依据进行相应的模糊运算,将结果去模糊化后代入式(5),计算出调节后的PID控制器参数值为
| $\left\{ \begin{align} & {{K}_{P}}=K_{P}^{\prime }+{{\left\{ {{e}_{i}},{{e}_{ci}} \right\}}_{P}}=K_{P}^{\prime }+\Delta {{K}_{P}} \\ & {{K}_{I}}=K_{I}^{\prime }+{{\left\{ {{e}_{i}},{{e}_{ci}} \right\}}_{I}}=K_{I}^{\prime }+\Delta {{K}_{I}}, \\ & {{K}_{D}}=K_{ID}^{\prime }+{{\left\{ {{e}_{i}},{{e}_{ci}} \right\}}_{D}}=K_{ID}^{\prime }+\Delta {{K}_{D}} \\ \end{align} \right.$ | (5) |
式中KP′、KI′、KD′均为PID控制参数的初始值,PID的参数可以根据系统的变化通过模糊推理进行实时调节,体现出控制算法的自适应性.
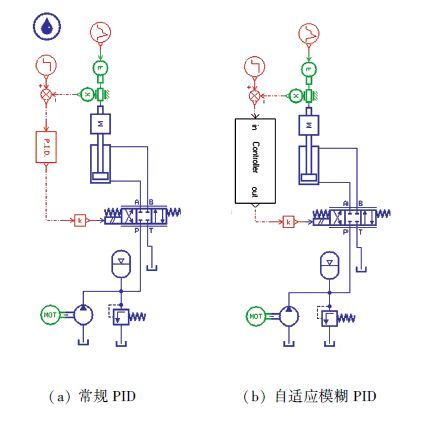
3 仿真分析 3.1 仿真模型为了评估算法的控制效果,在AMESim软件环境下建立了Hound机器人阀控缸系统模型,如图 5所示,模型中用到的主要参数如下:液压缸内径为25×10-3 m,活塞杆直径为14×10-3 m,液压缸行程为0.1 m,供油压力为16 MPa,油液密度为880 kg/m3,弹性模量为7×108 Pa,阀额定流量为10 L/min,阀额定电流为20 mA,阀频率为60 Hz,泵源流量为15 L/min,蓄能器容积为1 L,负载重量为20 kg.
|
图 5 AMESim阀控缸系统仿真模型 Figure 5 The AMESim simulation model of valve-controlled cylinder system |
利用联合仿真实现控制器设计,在Simulink中建立自适应模糊PID算法控制器,通过S-Function模块将控制结果实时送入AMESim模型中.
3.2 仿真结果使用图 5所示模型,通过试凑法得到一组较为满意的PID参数(P=15,I=0.05,D=0.03).为便于观察自适应模糊PID算法的调整能力,比较上述两种控制算法对于不同输入信号的跟踪效果,将式(5)中的PID初始值(KP′、KI′、KD′)设定为与常规PID相同的参数值.
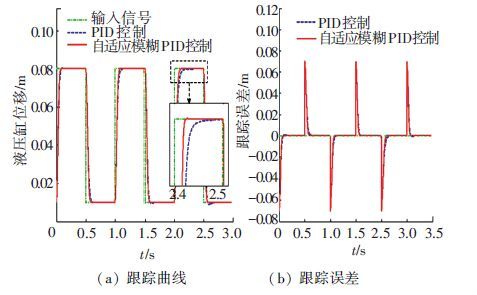
1) 方波信号跟踪.以机器人运行时液压缸常用行程(0.01~0.08 m)作为测试范围,设定输入信号为频率1 Hz的方波信号,并在1~2 s和2~3 s这两个时间段分别加入2、4 kN的外部负载(干扰)力(沿液压缸缩回方向).两种算法下阀控缸系统对方波信号的跟踪效果如图 6所示,调节时间的变化见表 2.
|
图 6 方波信号跟踪效果 Figure 6 The tracking effect for the square wave signal |
| 表 2 方波信号调节时间 Table 2 The adjusting time of square wave signal |
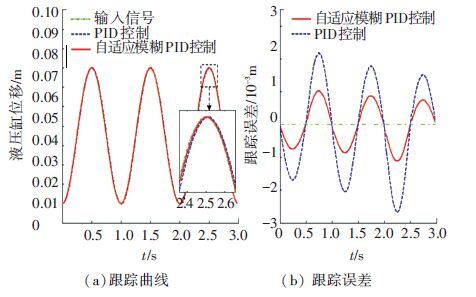
2) 正弦信号跟踪.设定频率为1 Hz的正弦波输入信号,跟踪效果和跟踪误差如图 7所示.
|
图 7 正弦信号跟踪效果 Figure 7 The tracking effect for the sinusoidal signal |
通过图 6、7和表 2可以看出,自适应模糊PID控制算法相比常规PID控制能有效减小系统的调节时间,提高跟踪速度和精度,并削弱外部干扰力对系统的影响,增强抑制干扰的能力,表现出更为优越的控制品质.
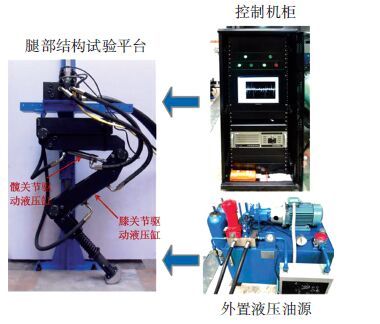
4 试 验自适应模糊PID算法在AMESim仿真中取得了较好的控制效果,但由于仿真模型与实际系统之间仍有一定的差别,为了验证实际的控制效果,搭建了Hound液压机器人的单腿试验平台(见图 8).该平台由机器人腿部结构、试验台架、外置液压油源、控制机柜(含工控机、数据采集板卡)等部分构成,并采用LABWindows+RTX的组合方式作为上位机的实时控制软件,可实现机器人腿部的周期运动和负载能力测试.下面以膝关节为控制对象进行性能测试,油源压力设定为10 MPa.
|
图 8 机器人单腿试验平台 Figure 8 The test platform of robot’s single leg |
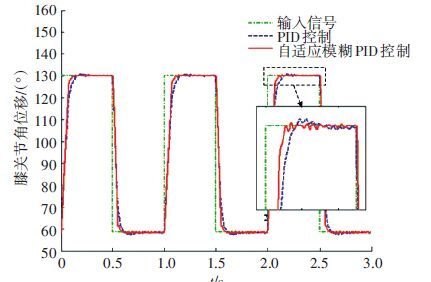
测试时采用与软件仿真时相同频率的输入信号.由于腿部关节的传感器采集的是角度数据,当膝关节的驱动液压缸位移为0.01~0.08 m时,对应的关节转动角度为58°~130°,以此作为测试的输入跟踪信号.为了验证控制效果,仍采用与常规PID控制进行对比的方式,测试曲线如图 9、10所示.
|
图 9 膝关节对方波信号跟踪效果 Figure 9 The tracking effect of knee joint for the square wave signal |

|
图 10 膝关节对正弦信号跟踪效果 Figure 10 The tracking effect of knee joint for the sinusoidal signal |
由于机械配合、运动摩擦、噪声等因素的影响,通过测试曲线可以看出,在单腿试验平台上使用自适应模糊PID算法对膝关节进行控制测试时,其对跟踪曲线的改善效果不如软件仿真时那样明显,但也能减少调节时间,减小超调量,其幅值衰减和相位滞后情况相比较于常规PID控制有一定的改善,能更好地跟踪设定的期望轨迹,因此该算法适合用于四足机器人的关节运动控制.
5 结 论1) 在分析液压机器人所采用的阀控非对称缸系统原理和控制难点基础上,将自适应模糊PID控制算法用于机器人腿部关节的运动控制,并使用AMESim/Simulink搭建的联合仿真模型及机器人单腿试验平台进行仿真和实物测试,结果表明自适应模糊PID控制提高了液压驱动系统应对非线性和参数时变等不良因素的能力.
2) 自适应模糊PID控制相比常规PID具有更好的动态响应性能,且易于工程应用,有利于实现机器人的运动控制.
| [1] |
RAIBERT M, BLANKESPOOR K, NELSON G, et al. BigDog,the rough-terrain quadruped robot[C]// Proceedings of the 17th World Congress the International Federation of Automatic Control.Seoul: IFAC, 2008: 10822-10825.
( 0) 0)
|
| [2] |
SEMINI C, TSAGARAKIS N G, GUGLIELMINO E, et al. Design of HyQ - a hydraulically and electrically actuated quadruped robot[J].
Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering,2011, 225 (6) : 831-849.
DOI: 10.1177/0959651811402275 ( 0) 0)
|
| [3] |
董建园, 曹旭妍, 魏培, 等. 电液比例位置控制系统的研究[J].
机床与液压,2013, 41 (7) : 40-47.
DONG Jianyuan, CAO Xuyan, WEI Pei, et al. Research on electro-hydraulic proportional position servo system[J]. Machine Tool & Hydraulics,2013, 41 (7) : 40-47. (  0) 0)
|
| [4] |
高炳微, 邵俊鹏, 韩桂华. 电液伺服系统位置和力模糊切换控制方法[J].
电机与控制学报,2014, 18 (5) : 99-104.
GAO Bingwei, SHAO Junpeng, HAN Guihua. Fuzzy switching control between position and force for electro-hydraulic servo system[J]. Electric Machines and Control,2014, 18 (5) : 99-104. (  0) 0)
|
| [5] |
张晓宁, 王岩, 付永领. 非对称液压缸对称性控制[J].
北京航空航天大学学报,2007, 33 (11) : 1334-1339.
ZHANG Xiaoning, WANG Yan, FU Yongling. Symmetric control of asymmetric cylinder[J]. Journal of Beijing University of Aeronautics and Astronautics,2007, 33 (11) : 1334-1339. (  0) 0)
|
| [6] |
AHN K K, TRUONG D Q. Online tuning fuzzy PID controller using robust extended Kalman filter[J].
Journal of Process Control,2009, 19 (6) : 1011-1023.
DOI: 10.1016/j.jprocont.2009.01.005 ( 0) 0)
|
| [7] |
曹正, 赵新泽, 陈永清. 阀控非对称液压缸往返运动动态特性对比分析[J].
机床与液压,2008, 36 (9) : 254-256.
CAO Zheng, ZHAO Xinze, CHEN Yongqing. Comparison of dynamic characteristics of asymmetric cylinder moved back and forth controlled by symmetric valve[J]. Machine Tool & Hydraulics,2008, 36 (9) : 254-256. (  0) 0)
|
| [8] |
MANRING N D.
Hydraulic control system[M]. New Jersey: John Wiley & Sons, Inc, 2005 .
( 0) 0)
|
| [9] |
SABAN C, ALI V A. Simulation and hybrid fuzzy-PID control for positioning of a hydraulic system[J].
Nonlinear Dynamics,2010, 61 (3) : 465-476.
DOI: 10.1007/s11071-010-9662-1 ( 0) 0)
|
| [10] |
JELALI M, KROLL A.
Hydraulic servo-systems: modelling, identification, and control[M]. New Jersey: Springer, 2003 .
( 0) 0)
|
| [11] |
JIN Junran, HUANG Hengshuo, SUN Junman, et al. Study on fuzzy self-adaptive PID control system of biomass boiler drum water[J].
Journal of Sustainable Bioenergy Systems,2013, 3 (1) : 93-98.
DOI: 10.4236/jsbs.2013.31013 ( 0) 0)
|
| [12] |
ESFANDYARI M, FANAEI M A, ZOHREIE H. Adaptive fuzzy tuning of PID controllers[J].
Neural Computing and Applications,2013, 23 (1) : 19-28.
( 0) 0)
|
| [13] |
SIVANANDAM S N, SUMATHI S, DEEPA S N.
Introduction to fuzzy logic using Matlab[M]. Berlin: Verlag Berlin Heidelberg, 2007 .
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


