2. 中车大连电力牵引研发中心,辽宁 大连 116024
2. 2.CRRC Dalian Electric Traction R & D Center,Dalian 116024,Liaoning,China
近年来,我国高速铁路建设取得了快速发展,改变了原有交通运输格局,缓解了我国铁路运输紧张状况,促进了国民经济快速健康发展. 在电力机车、动车组及城市轨道交通中,“逆变器-牵引电机” 系统是列车的关键部件,其控制方案主要有矢量控制和直接转矩控制两大类,对列车的高可靠与高性能运行起着至关重要的作用. 直接转矩控制具有系统结构简单,动态响应快,对电动机参数依赖小等优点,非常适合电力牵引传动系统中负载复杂多变的情况;然而,其也存在转矩脉动较大,开关频率不固定以及系统低速稳定性较差等缺点. 针对上述问题,专家学者对传统直接转矩控制提出了很多改进方案,其中由M. Depenbrock提出的间接定子量控制(indirect stator-quantities control,ISC)方案是其中比较有代表性的一种[1]. 间接定子量控制是一种结合了传统直接转矩控制和空间电压矢量调制的新算法,它保留了直接转矩控制系统结构简单和动态响应较快的优点,同时固定了开关频率,减小了转矩脉动,因此非常适合轨道交通等对系统运行稳定性要求较高的场合[2]. 目前,牵引逆变器在拓扑结构、控制策略、调制方法和系统优化等方面已经得到成熟应用,正朝着高速、重载等方向迈进[3-6]. 然而,在其性能不断提升的同时,其运行的安全性和可靠性研究同样需要引起足够的关注和重视. 牵引逆变器长期运行于高压、大电流工作状态下,IGBT等功率开关器件易发生开路或短路故障,导致牵引逆变器无法正常工作. 为了保证牵引逆变器发生故障后电力机车能够继续运行(特别是运行于桥梁、隧道和坡路时),研究在容错状态下电力牵引传动系统的控制方案具有重要意义. 文献[7-11]提出了三相四开关容错逆变器的空间矢量脉宽调制策略,实现了异步电机的矢量控制. 文献[12]提出了逆变器故障条件下异步电机的直接转矩控制方案,并对两种不同容错拓扑的控制效果进行了对比分析. 然而,对于功率开关器件故障条件下的“牵引电机间接定子量控制”容错策略目前尚没有文献报道;同时,针对牵引逆变器四开关运行后所引起的电容中点电压不平衡问题,已有研究成果尚不完善,如被控对象建模不精确、补偿控制策略缺乏理论设计依据以及补偿效果不理想等问题.
有鉴于此,本文设计了基于三相四开关容错逆变器的牵引电机间接定子量控制方案,阐述了四开关SVPWM算法的具体实现过程,针对四开关逆变器直流侧电容中点电压不平衡的问题,通过电路分析和数学建模建立了中点电压补偿模型,提出了一种基于PID调节器的补偿算法. 最后在MATLAB/Simulink平台中建立了控制系统的仿真模型,对系统进行了仿真实验分析,结果证明了本文所提出的系统容错控制方案和电容中点电压补偿算法的可行性和有效性.
1 四开关容错间接定子量控制方案 1.1 控制系统结构当六开关牵引逆变器某一相出现开路或短路故障后,为保证电力机车继续运行,可将故障相切除,使系统运行在四开关容错状态下.
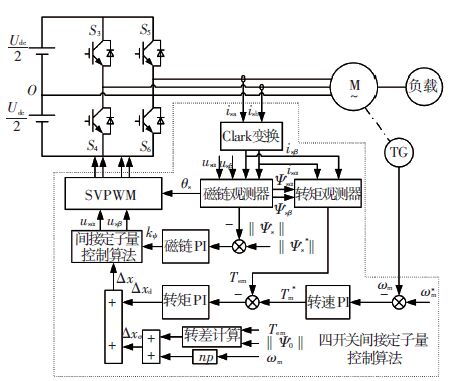
采用间接定子量控制方案的四开关牵引交流传动系统如图 1所示. 系统由三相四开关主回路、检测电路以及控制电路等几部分组成. 其主回路直流侧支撑电容由两个参数相同的电容器串联构成,将故障相电机绕组直接连接到直流侧电容中点上,构成电机三相四开关供电方式. 主回路实现对牵引电机的驱动功能,检测电路用来测量牵引电机的定子电压、电流和转速信号,控制电路实现四开关间接定子量控制算法及控制信号的SVPWM调制.
|
图 1 牵引电机四开关间接定子量控制系统结构 Figure 1 Four-switch ISC syetem of traction motor |
间接定子量控制是对传统直接转矩控制的一种改进方案,根据当前的转矩给定值、磁链给定值以及计算出来的磁链和转矩来估算下一个PWM周期中定子磁链所要求的幅值和角度变化,从而推算出定子电压矢量,再通过空间矢量脉宽调制得到逆变器的控制信号.
将电磁转矩和磁链的比较差值分别进行PI调节,转矩PI调节输出下一周期定子磁链角度的动态增量Δxd,磁链PI调节输出磁链幅值的动态增量kψ. 控制过程中,定子磁链在向前运动,设其在一个周期内所扫过的电角度为Δxσ,Δxσ包括转子磁链转速和转差转速. 转差转速计算公式为
| ${{\omega }_{sl}}={{T}_{e}}{{R}_{r}}/({{n}_{p}}{{\psi }^{2}}_{s}).~$ | (1) |
可以推导出
| $\Delta {{x}_{\sigma }}=[{{n}_{p}}{{\omega }_{r}}+{{T}_{e}}{{R}_{r}}/({{n}_{p}}{{\psi }^{2}}_{s})]\cdot {{T}_{s}}.$ | (2) |
本控制周期结束时,定子磁链的位置角表达式为
| ${{\theta }_{(k)}}={{\theta }_{(k-1)}}+\Delta {{x}_{\sigma }}+\Delta {{x}_{d}}.$ | (3) |
磁链幅值的表达式为
| $|{{\psi }_{s(k)}}|=(1+{{k}_{\psi }})|{{\psi }_{s(k-1)}}|.$ | (4) |
在控制周期内定子磁链的增量Δψ为
| $\begin{align} & \Delta \psi ={{\psi }_{s(k)}}-{{\psi }_{s(k-1)}}=(1+{{k}_{\psi }}){{\psi }_{s(k-1)}}{{e}^{j{{\theta }_{ref}}}}-{{\psi }_{s(k-1)}}{{e}^{j\theta }}={{\psi }_{s(k-1)}}\{[(1+{{k}_{\psi }}) \\ & cos(\theta +\Delta {{x}_{d}}+\Delta {{x}_{\sigma }})-cos~\theta \left] +j \right[(1+{{k}_{\psi }})sin(\theta +\Delta {{x}_{d}}+\Delta {{x}_{\sigma }})-sin~\theta ]\} \\ \end{align}$ | (5) |
进而,根据牵引异步电机的数学模型为
| ${{u}_{s}}={{R}_{s}}{{i}_{s}}+\frac{d{{\psi }_{s}}}{dt}.$ | (6) |
电机参考电压矢量为
| $\left\{ \begin{matrix} {{u}_{s\alpha }}={{R}_{s}}{{i}_{s\alpha }}+{{\frac{\Delta {{\psi }_{s\alpha }}}{T}}_{s}}, \\ {{u}_{s\beta }}={{R}_{s}}{{i}_{s\beta }}+{{\frac{\Delta {{\psi }_{s\beta }}}{T}}_{s}}. \\ \end{matrix} \right.$ | (7) |
将间接定子量控制用于三相四开关容错逆变器时,由于没有电流闭环,无法直接对直流侧两个电容中点的电压进行调节. 在控制中仅考虑了对电磁转矩的迅速调节,因此会导致直流侧电容中点电压的不平衡,甚至导致系统失控. 文中后续内容将详细分析和解决直流侧电容中点电压不平衡的问题.
1.3 磁链和电磁转矩观测模型间接定子量控制系统中,定子磁链和电磁转矩的观测模型分别为
| $\left\{ \begin{matrix} {{\psi }_{s\alpha }}=\int ({{u}_{s\alpha }}-{{R}_{s}}{{i}_{s\alpha }})dt, \\ {{\psi }_{s\beta }}=\int ({{u}_{s\beta }}-{{R}_{s}}{{i}_{s\beta }})dt. \\ \end{matrix} \right.$ | (8) |
| ${{T}_{e}}=\frac{3}{2}p({{\psi }_{s\alpha }}{{i}_{s\beta }}-{{\psi }_{s\beta }}{{i}_{s\alpha }}).$ | (9) |
磁链观测采用常用的电压模型法,电压模型法是一纯积分环节,实际中,由于测量噪声、误差积累以及直流偏移等非理想因素的影响,使得电动机在低速运行时采用纯积分器很难实现定子磁链的准确计算.
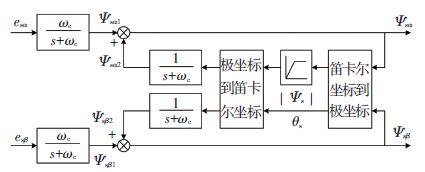
为了抑制定子磁链的积分漂移,可以采用以低通滤波器为基础的改进型积分器. 本文采用的改进型积分器的结构如图 2所示,它增加了反馈通道,在反馈通道中,对从两个前向通道来的信号进行从笛卡尔坐标到极坐标的变换,变成幅值和相角信号,把磁链的幅值和相角限制在给定的范围内,抑制传统电压模型法的积分漂移问题.
|
图 2 改进的定子磁链积分模型 Figure 2 Improved integral model of stator flux |
传统的六开关逆变器供电牵引传动系统具有8个空间电压矢量,包括6个有效电压矢量和两个零矢量. 当系统工作在四开关状态时,由于只有4个开关工作,故障相不可控,因此四开关系统的有效电压矢量减少为4个.
对于图 1所示的三相四开关系统,假定a相为故障相,以Sb和Sc表示b、c两相的开关状态,上管导通时值为1,下管导通时值为0,直流侧两个电容上的电压均为Udc/2,则在两相静止坐标系下,系统定子电压可表示为
| $\left\{ \begin{matrix} {{u}_{s\alpha }}={{U}_{dc}}(1-{{S}_{b}}-{{S}_{c}})/3, \\ {{u}_{s\beta }}={{U}_{dc}}({{S}_{b}}-{{S}_{c}})/3 \\ \end{matrix} \right.$ | (10) |
其空间电压矢量为
| ${{u}_{s}}={{u}_{s\alpha }}+j{{u}_{s\beta }}=2{{U}_{dc}}(0.5+\alpha {{S}_{b}}+{{\alpha }^{2}}{{S}_{c}})/3.$ | (11) |
式中α=ej120°.
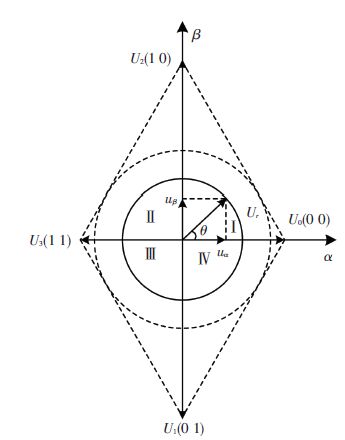
根据式(10)、(11),四开关系统的空间电压矢量见表 1,在αβ平面表示如图 3所示. 可见,四开关系统共有4种开关状态,对应4个有效空间电压矢量,电压矢量的幅值不等,两两对称,相位依次相差90°,没有零矢量,若控制中需要使用零矢量,可以采用幅值相等、方向相反的一对有效电压矢量来合成.
| 表 1 四开关逆变器的空间电压矢量 Table 1 Space voltage vectors of four-switch inverter |
|
图 3 四开关逆变器的空间电压矢量 Figure 3 Space voltage vectors of four-switch inverter |
SVPWM算法在牵引传动领域应用广泛,它从电机的角度出发,通过逆变器开关器件的不同开关模式产生实际磁链去逼近基准圆形磁链,具有较好的控制性能. 与传统的SPWM相比,SVPWM开关次数少、直流电压利用率高、谐波抑制效果好,且易于数字化实现.
如图 3所示,以第I扇区为例,Ur的相角记为θ,U0和U2为用于合成参考电压矢量的两个相邻矢量,则有
| ${{U}_{r}}T={{T}_{x}}{{U}_{0}}+{{T}_{y}}{{U}_{2}}.$ | (12) |
根据矢量合成的基本原则,可以推导出U0和Ur的作用时间分别为
| $\left\{ \begin{matrix} {{T}_{x}}=\frac{3\left| {{U}_{r}} \right|}{{{U}_{dc}}}Tcos~\theta , \\ {{T}_{y}}=\frac{\sqrt{3}|{{U}_{r}}|}{{{U}_{dc}}}Tsin~\theta , \\ {{T}_{0}}=T-{{T}_{x}}-{{T}_{y}}. \\ \end{matrix} \right.$ | (13) |
其中:T为采样周期;T0为零矢量作用的时间;Udc为直流母线电压.
在传统的六开关系统中,除了基本电压矢量外,还有两个零矢量,时间T0通过施加零矢量来实现. 但在四开关系统中,只有4个基本电压矢量,没有零矢量,一般通过在相同的时间内施加两个相反方向的电压矢量来等效零矢量的作用.
实际中,为了减少开关次数,降低开关损耗和抑制谐波,可采用“七段式”四开关SVPWM来确定开关模式:每一调制周期以U0开始和结束,每个周期内同一桥臂上开关器件的开关状态只改变两次. 一般通过采用三角波调制的方式实现“七段式”四开关SVPWM,如图 4所示.

|
图 4 “七段式”四开关SVPWM波形 Figure 4 Seven-segment mode four-switch SVPWM waveform |
综上,四开关SVPWM控制算法流程可由图 5表示,主要分为扇区判断、占空比计算和PWM调制等几部分. 通过SVPWM控制的逆变器可以输出三相对称的正弦基波电压,使电机形成圆形磁链轨迹.

|
图 5 四开关SVPWM算法流程 Figure 5 Algorithm process of four-switch SVPWM |
对于电流闭环控制系统,由于电容充放电的多少由有功电流指令值决定,因此将电压差值的平均值通过PI控制器得到需要补偿的有功电流值,与原有功指令电流相加即得到新的有功指令电流,这样即可动态地调整直流侧两个电容上的电压平衡,以消除直流分量[13].
采用的是间接定子量控制算法,由于没有电流闭环,因此无法直接通过补偿有功电流的方式来调节直流侧电容电压的平衡. 本文基于对电容充放电过程的建模与分析,提出了电压补偿的方案,具体分析如下.
四开关系统的直流侧采用两个电容串联的方式,理想情况下两个电容上的电压相等,电容中点的电压等于零. 实际中,由于两个电容的参数不可能完全相同,电容器老化造成的参数变化以及负载的波动等都会造成电容电压的不平衡,给系统的控制造成不利的影响.
设不平衡条件下电容C1和C2两端的电压分别为(Udc+ΔU)/2和(Udc-ΔU)/2,两个电容上的电压差为ΔU.
电容电压不平衡时,在两相静止坐标系下,电动机相电压与开关信号的关系可表示为
| $\left[ \begin{matrix} {{u}_{s\alpha }} \\ {{u}_{s\beta }} \\ \end{matrix} \right]=\frac{2}{3}{{U}_{dc}}\left[ \begin{matrix} 1 & -\frac{1}{2} & -\frac{1}{2} \\ 0 & \frac{\sqrt{3}}{2} & \frac{\sqrt{3}}{2} \\ \end{matrix} \right]\left[ \begin{matrix} \frac{1}{2} \\ {{s}_{b}} \\ {{s}_{c}} \\ \end{matrix} \right]+\left[ \begin{matrix} \frac{-\Delta U}{3} \\ 0 \\ \end{matrix} \right].$ | (14) |
根据式(14)可知,直流侧电容电压的不平衡造成了定子电压α轴分量的偏移,导致三相电压和电流不对称,给电机控制带来不利的影响.
电容电压不平衡主要是故障相绕组电流对两个电容充放电造成的,如果故障相电流为理想正弦,则两个电容的电压差也为正弦量. 可以通过补偿定子电压偏移的方法来调节直流侧电容的电压差,使直流侧电容中点电压平衡. 采用补偿定子电压α轴分量的方案,设补偿电压为ΔU1,则
| $\left\{ \begin{matrix} {{u}^{\prime }}_{s\alpha }={{u}_{s\alpha }}-\Delta {{U}_{1}} \\ {{u}^{\prime }}_{s\beta }={{u}_{s\beta }}. \\ \end{matrix} \right.$ | (15) |
根据Clarke变换可以推导出
| $\left\{ \begin{matrix} {{u}^{\prime }}_{a}={{u}_{a}}-\Delta {{U}_{1}}, \\ {{u}^{\prime }}_{b}={{u}_{b}}+12\Delta {{U}_{1}}, \\ {{u}^{\prime }}_{c}={{u}_{c}}+12\Delta {{U}_{1}}. \\ \end{matrix} \right.$ | (16) |
当C1=C2时,两个电容上的电压Udc1=Udc2=Udc/2. 假设C2 <C1,则Udc2 >Udc1,ΔU=Udc1-Udc2<0,令ΔU1=f(ΔU),其中f(·)为控制律,并保证ΔU1与ΔU同号,根据式(16)可知,通过补偿可使故障相电压产生正的偏移量,从而使故障相电流产生正的偏移量Δia.
下面分析在不同电压矢量作用下,Δia对直流侧电容电压差的影响.
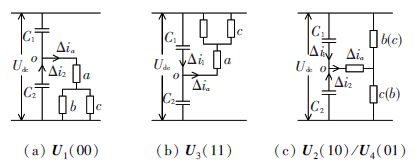
1) 矢量U1(0 0)作用. 等效电路如图 6(a)所示,电容C2通过负载电流放电,直流电源对电容C1充电,从而使两个电容的电压差|ΔU|减小,有利于直流侧电容电压平衡.
|
图 6 四开关逆变器等效电路 Figure 6 Equivalent circuit of four-switch inverter |
2) 矢量U3(1 1)作用. 等效电路如图 6(b)所示,负载电流对电容C1充电,电容C2通过直流电源放电,从而使两个电容的电压差|ΔU|减小,有利于直流侧电容电压平衡.
3 )矢量U2(1 0)或U4(0 1)作用. 等效电路如图 6(c)所示,电容C1通过负载电流充电,C2通过负载电流放电,两个电容的电压差|ΔU|减小,有利于直流侧电容电压平衡.
综上所述,通过补偿定子电压α轴分量的方法可以调节直流侧两个电容上的电压差,使其趋近于0. 对于C2 >C1的情况,通过分析可以得到类似的结论.
前述补偿电压ΔU1=f(ΔU),ΔU1作用在电动机定子上产生补偿电流Δia,由于电动机可等效成阻感性负载,因此Δia对于ΔU1的响应具有一阶惯性特性,同时Δia对电容的充放电可等效为积分环节,设被补偿的电压差为ΔU2,则
| $\Delta {{U}_{2}}=\frac{K\Delta {{U}_{1}}}{s({{T}_{s}}s+1)}.$ | (17) |
其中K为常数,Ts为电动机的滞后时间常数.
由牵引异步电机在三相静止坐标系中的数学模型可知,时间常数Ts是转子位置角θ的非线性函数,这给系统的控制造成了一定的困难. 一般情况下Ts<<1,为了简化控制律的设计,可以忽略Ts的影响,近似得到
| $\Delta {{U}_{2}}=\frac{K\Delta {{U}_{1}}}{s}.$ | (18) |
本文采用式(18)所示的电容中点电压补偿模型,根据经典控制理论,控制率f(·)可以采用简单的比例控制,系统开环传递函数简化为纯积分环节,通过调节控制器的比例系数即可控制电容电压达到平衡的时间.
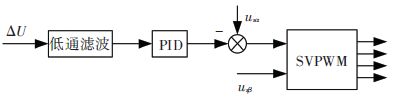
3.2 电容中点电压平衡控制方案如图 7所示,ΔU为直流侧电容上的电压差,通过低通滤波器得到其直流分量,再经过PID调节器以提高补偿的动态响应速度和消除稳态误差,PID调节器输出(取负)和定子电压α轴给定值相加得到修正后的参考电压,经过四开关空间电压矢量调制,得到逆变器的开关信号. 由于电机故障相和逆变器直流侧电容中点相连,对电容的充放电导致电容中点电压波动,这是无法避免的,通过低通滤波器滤除波动分量,只对电容中点电压的直流分量进行补偿,可以减小过度补偿对系统性能造成的影响,保证系统的稳定性.
|
图 7 电容中点电压平衡控制算法流程 Figure 7 Neutral voltage balance control algorithm |
为了验证本文所设计基于容错逆变器的牵引电机间接定子量控制方案的可行性和有效性,在MATLAB/Simulink环境下搭建了系统的仿真模型,并对系统进行了仿真实验与分析. 实验相关参数为:电机额定功率1 224 kW,额定转速17 19.1 r/min,额定转矩6 800 N·m,启动转矩9 717 N·m,定子额定磁链3 Wb,定子电阻0.024 209 Ω,定子漏感0.294 mH,转子电阻0.018 817 Ω,转子漏感0.585 mH,定转子互感18.51 mH,逆变器开关频率1 kHz[13].
1) 启动和稳态特性. 转速给定为600 r/min,定子磁链给定为3 Wb,启动转矩设定为9 717 N·m,电动机带额定负载(6 800 N·m)启动时转速、电磁转矩、定子电流和磁链的波形如图 8所示.

|
图 8 启动和稳态特性 Figure 8 Startup and steady performance |
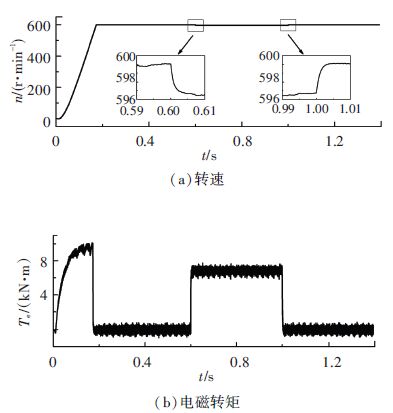
2) 动态特性. 电动机空载启动,0.6 s时负载转矩由0突加为6 800 N·m,1.0 s时负载转矩由6 800 N·m突减为0,转速和电磁转矩的波形如图 9所示.
|
图 9 动态特性 Figure 9 Dynamic performance |
3)电容中点电压补偿. 为了验证设计的电容中点电压补偿算法的效果,逆变器直流侧两个电容的值分别选取为C1=4.7 F,C2=4.5 F,电动机带额定负载(6 800 N·m)启动.
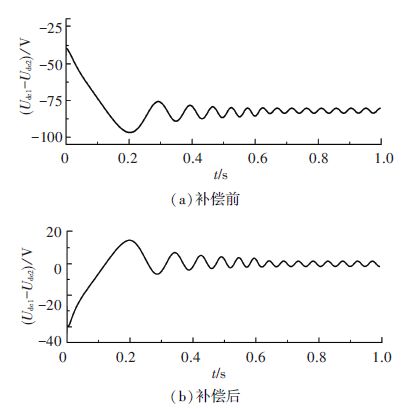
直流侧电容电压差如图 10所示,图 10(a)为补偿前的实验结果,图 10(b)为补偿后的实验结果.
|
图 10 直流侧电容电压差 Figure 10 Voltage difference of the capacitors |
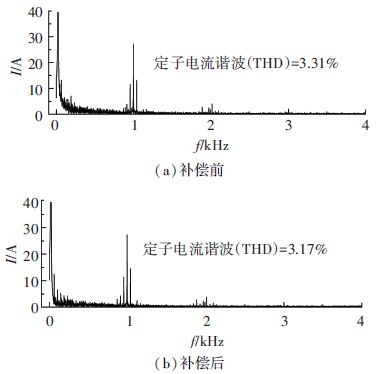
故障相定子电流频谱如图 11所示,图 11(a)为补偿前的实验结果,图 11(b)为补偿后的实验结果.
|
图 11 故障相定子电流频谱 Figure 11 Stator current spectrum of the fault phase |
由以上实验结果可见,牵引系统在三相四开关容错控制下稳定运行,电磁转矩和磁链的脉动均控制在工程允许的范围内,最大转矩脉动为1 000 N·m(10.2%),最大磁链脉动0.2 Wb(6.7%);对于负载的满负荷突变,电动机的转速波动小于0.7%,动态调整时间小于10 ms;直流侧电容中点电压补偿后,电压差的均值为0,故障相定子电流谐波(THD)降低0.14%.
5 结 论1) 针对逆变器功率器件故障条件下的电力牵引传动控制系统,给出一种牵引电机驱动器的三相四开关间接定子量容错控制方案.
2) 其在三相四开关容错拓扑的基础上,采用间接定子量控制算法,固定了逆变器开关频率,有效地减小了电磁转矩的脉动.
3) 基于直流侧中点电压模型,给出电压补偿控制的PID方案,取得了较好的补偿效果. 理论分析和仿真实验结果表明:所述的“三相四开关间接定子量容错控制方案”对于一类牵引电机的高可靠驱动控制,具有一定的实用价值.
| [1] |
冯晓云.
电力牵引交流传动及其控制系统[M]. 北京: 高等教育出版社, 2009 : 196 -200.
FENG Xiaoyun. AC drive and control system for electric traction[M]. Beijing: Higher Education Press, 2009 : 196 -200. (  0) 0)
|
| [2] |
尚敬, 刘可安. 电力牵引异步电动机无速度传感器间接定子量控制[J].
电工技术学报,2007, 22 (2) : 22-27.
SHANG Jing, LIU Kean. Speed sensorless indirect stator-quantities control of induction motor in electric traction[J]. Transaction of China Electrotechnical Society,2007, 22 (2) : 22-27. (  0) 0)
|
| [3] |
薛劭申, 许海平, 方程, 等. 多相永磁同步电机PWM技术[J].
哈尔滨工业大学学报,2014, 46 (4) : 122-128.
XUE Shaoshen, XU Haiping, FANG Cheng, et al. Study of the PWM technology of multiphase permanent magnet synchronous motor[J]. Journal of Harbin Institute of Technology,2014, 46 (4) : 122-128. (  0) 0)
|
| [4] |
王斌, 王跃, 王兆安. 无速度传感器的永磁同步电机无差拍直接转矩控制方法[J].
电机与控制学报,2014, 18 (6) : 42-49.
WANG Bin, WANG Yue, WANG Zhaoan. Deadbeat direct torque control of permanent magnet synchronous motor without speed sensor[J]. Electric Machines and Control,2014, 18 (6) : 42-49. (  0) 0)
|
| [5] |
王琛琛, 周明磊, 游小杰. 大功率交流电力机车脉宽调制方法[J].
电工技术学报,2012, 27 (2) : 173-178.
WANG Chenchen, ZHOU Minglei, YOU Xiaojie. Research on the PWM method of high power AC electrical locomotive[J]. Transaction of China Electrotechnical Society,2012, 27 (2) : 173-178. (  0) 0)
|
| [6] |
刘建强, 郑琼林, 杨其林. 高速列车牵引传动系统与牵引网谐振机理[J].
电工技术学报,2013, 28 (4) : 221-227.
LIU Jianqiang, ZHENG Qionglin, YANG Qilin. Resonance mechanism between traction drive system of high-speed train and traction network[J]. Transaction of China Electrotechnical Society,2013, 28 (4) : 221-227. (  0) 0)
|
| [7] |
安群涛, 孙醒涛, 赵克, 等. 容错三相四开关逆变器控制策略[J].
中国电机工程学报,2010, 30 (3) : 14-20.
AN Quntao, SUN Xingtao, ZHAO Ke, et al. Control strategy for fault-tolerant three-phase four-switch inverters[J]. Proceedings of The Chinese Society for Electrical Engineering,2010, 30 (3) : 14-20. (  0) 0)
|
| [8] |
刘宏超, 吕胜民, 张春晖. 三相四开关的并联型有源电力滤波器的SVPWM调制算法[J].
电工技术学报,2011, 26 (4) : 128-134.
LIU Hongchao, LV Shengmin, ZHANG Chunhui. Space vector pulse width modulation of three-phase four-switch shunt active power filter[J]. Transaction of China Electrotechnical Society,2011, 26 (4) : 128-134. (  0) 0)
|
| [9] |
ZHANG Jianghan, JIN Zhao, ZHOU Dehong. High-performance fault diagnosis in PWM voltage-source inverters for vector-controlled induction motor drives[J].
IEEE Transaction on Power Electronics,2014, 29 (11) : 6087-6099.
DOI: 10.1109/TPEL.2014.2301167 ( 0) 0)
|
| [10] |
LEE T, JIA Hongliu. Modeling and control of a three-phase four-switch PWM voltage-source rectifier in d-q synchronous frame[J].
IEEE Transaction on Power Electronics,2011, 26 (9) : 2476-2489.
DOI: 10.1109/TPEL.2011.2108318 ( 0) 0)
|
| [11] |
MASMOUDI M, BADSI B, MASMOUDI A. DTC of B4-inverter-fed BLDC motor drives with reduced torque ripple during sector-to-sector commutation[J].
IEEE Transaction on Power Electronics,2014, 29 (9) : 4855-4865.
DOI: 10.1109/TPEL.2013.2284111 ( 0) 0)
|
| [12] |
张兰红, 胡育文, 黄文新. 基于直接转矩控制技术的异步电机驱动系统两种容错方案研究[J].
南京航空航天大学学报,2005, 31 (1) : 34-39.
ZHANG Lanhong, HU Yuwen, HUANG Wenxin. Two tolerant schemes for induction machine drive system based on DTC strategy[J]. Journal of Nanjing University of Aeronautics and Astronautics,2005, 31 (1) : 34-39. (  0) 0)
|
| [13] |
郭世明.
机车动车牵引交流传动技术[M]. 北京: 机械工业出版社, 2012 : 6 -12.
GUO Shiming. AC drive technology for locomotive traction[M]. Beijing: China Machine Press, 2012 : 6 -12. (  0) 0)
|
 2016, Vol. 48
2016, Vol. 48


