在装备制造领域中,长轴类零件的应用比较广泛. 要想实现精密长轴类零件的机械化装配,需要解决长轴类零件三维位姿的快速、精确检测问题. 由于长轴类零件端部易发生挠曲变形且轴类零件一般由一端进行装配,因此,研究长轴类零件装配端位姿的检测方法对提升制造业的自动化水平具有重要的意义.
在零件位姿的自动化检测方法中,基于机器视觉的位姿检测方法近年来受到相关学者的广泛重视[1-2],并在基于机器视觉引导工业机器人进行抓取、搬运、装配等相关领域得到应用[3-5]. 迄今为止,虽然基于单目相机的机器视觉也可以通过检测零件的位姿引导机器人进行作业[6],但由于单目相机属于平面视觉,不能检测出零件在相机拍摄方向的深度信息,因此,单目相机引导机器人的操作只能局限于某一固定平面内. 为了实现三维位姿的检测,采用基于视差原理构建的双目相机立体视觉检测系统得到应用[7-8].
采用平行双目或斜交双目的非正交双目立体视觉在检测零件的三维位姿时必须进行多个特征点的匹配[2, 4, 7-9],而轴类零件的圆柱表面一般没有明显的特征点,难以直接利用轴类零件自身的特征点通过三维重构来获得轴类零件的三维位姿信息. 因此,有学者分别采用通过激光射线照射的方法在圆柱表面人为创造特征点进而检测圆柱[10]、圆筒型锻件[11]、圆截面飞机导管[12]的三维尺寸或位姿. 虽然该方法可以检测圆柱形零件的位姿信息,但是其检测精度依赖于发射激光的准确性和稳定性,并且增加了检测系统的成本. 因此,该方法在依据双目机器视觉检测轴类零件的位姿信息来引导机器人进行快速、精密装配方面存在不足. 郭玉波等[13]通过仿真实验对双目视觉结构参数进行优化,得出了采用两个相机的光轴互相垂直的正交双目视觉的检测误差值最小的结论,为双目立体视觉的应用提供了新的思路.
本文针对非正交双目立体视觉在引导机器人进行长轴类零件位姿检测方面的不足,提出了一种通过正交双目立体视觉来快速检测长轴类零件装配端三维位姿的方法:首先,建立正交双目立体视觉模型; 其次,给出长轴类零件装配端位姿检测的方法; 最后,通过实验验证了该方法在长轴类零件装配端三维位姿检测方面的可行性,为通过机器视觉引导机器人进行精密轴类零件的快速装配奠定了基础.
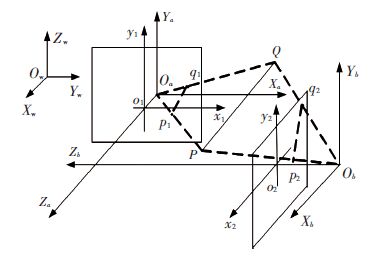
1 正交双目立体视觉模型正交双目立体视觉系统是由两个光轴正交的相机构成的,检测任意空间线段PQ三维信息的模型如图 1所示,其中Ow-XwYwZw为世界坐标系,Oa-XaYaZa和o1-x1y1分别为相机A的相机坐标系和图像坐标系,Ob-XbYbZb和o2-x2y2分别为相机B的相机坐标系和图像坐标系,且相机B的光轴Zb和A相机的光轴Za正交,p1q1和p2q2分别为被检测线段PQ在o1-x1y1和o2-x2y2上的投影.
|
图 1 正交双目立体视觉模型 Figure 1 Model of orthogonal binocular stereovision |
根据相机成像原理可知:空间点P在相机A坐标系下的坐标值(Xa,Ya,Za)与其在相机A的图像坐标系中成像平面上的投影点p1的像素坐标值(ua,va)之间的关系为
| $\left\{ \begin{array}{l} {u_a} = {f_{xa}}{X_a}/{Z_a} + {u_{0a}},\\ {v_a} = {f_{ya}}{Y_a}/{Z_a} + {v_{0a}}. \end{array} \right.$ | (1) |
式中:${f_{xa}} = {f_a}/d{x_a},{f_{ya}} = {f_a}/d{y_a}$,fa为相机A的焦距,dxa、dya分别为相机A的像元宽和像元高,u0a、v0a分别为相机A的像素坐标原点. 以上参数均为相机A的内参数,可以通过对相机A的标定而确定[14-15],具体标定方法本文不再赘述.
由式(1)可知,当已知点P在相机A坐标系下的坐标值为(Xa,Ya,Za)时,通过标定相机A的内部参数便可求出该点在相机图像坐标系中的坐标(ua,va);但是,当已知点P在相机A的图像坐标系中的坐标值(ua,va)时,无法确定点P在相机A坐标系下的坐标值(Xa,Ya,Za),仅仅可以确定点P在一条过相机光心Oa和点p1的直线上,表明使用单目相机无法检测到空间点P的深度信息.
对于相机B,同理可得出空间点P在相机B坐标系下的坐标值(Xb,Yb,Zb)与其在相机B的图像坐标系中成像平面上的投影点p2的像素坐标值(ub,vb)之间的关系为
| $\left\{ \begin{array}{l} {u_b} = {f_{xb}}\frac{{{X_b}}}{{{Z_b}}} + {u_{0b}},\\ {v_b} = {f_{yb}}\frac{{{Y_b}}}{{{Z_b}}} + {v_{0b}}. \end{array} \right.$ | (2) |
式中:${f_{xb}} = {f_b}/d{x_b},{f_{yb}} = {f_b}/d{y_b}$,fb为相机B的焦距,dxb、dyb分别为相机B的像元宽和像元高,u0b、v0b分别为相机B的像素坐标原点. 以上参数均为相机B的内参数,同理可以通过对相机B的标定而确定.
由于相机B的光轴Zb和相机A的光轴Za正交,因此相机B的坐标系Ob-XbYbZb可以看作由相机A的坐标系Oa-XaYaZa绕Ya轴旋转-90°后再将坐标原点平移到Ob得到. 于是可知空间点P在相机B坐标系下的坐标值(Xb,Yb,Zb)与其在相机A的坐标系下的坐标值(Xa,Ya,Za)存在如下关系:
| $\left[ \begin{array}{*{35}{l}} {{X}_{b}} \\ {{Y}_{b}} \\ {{Z}_{b}} \\ \end{array} \right]=R_{ba}^{-1}\left( \left[ \begin{array}{*{35}{l}} {{X}_{b}} \\ {{Y}_{b}} \\ {{Z}_{b}} \\ \end{array} \right]-{{T}_{ba}} \right),$ | (3) |
| ${{R}_{ba}}=\left[ \begin{matrix} 0 & 0 & -1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \\ \end{matrix} \right],$ | (4) |
| ${{T}_{ba}}=\left[ \begin{matrix} {{T}_{bax}} \\ {{T}_{bay}} \\ {{T}_{baz}} \\ \end{matrix} \right].$ |
式中:Rba和T
将式(3)代入式(2)并与式(1)联立,便可根据空间点P分别在相机A和相机B中的投影点p1和p2在各自图像坐标系中的像素坐标值(ua,va)和(ub,vb)计算出点P在相机A坐标系Oa-XaYaZa中的坐标值(Xa,Ya,Za):
| $\left[ \begin{array}{l} {X_a}\\ {Y_a}\\ {Z_a} \end{array} \right] = \left[ \begin{array}{l} \frac{{({u_a} - {u_{0a}})({f_{xb}}{T_{baz}} + ({u_b} - {u_{0b}}){T_{bax}})}}{{{f_{xa}}{f_{xb}} + ({u_a} - {u_{0a}})({u_b} - {u_{0b}})}}\\ \frac{{({v_a} - {v_{0a}}){f_{xa}}({f_{xb}}{T_{baz}} + ({u_b} - {u_{0b}}){T_{bax}})}}{{{f_{ya}}({f_{xa}}{f_{xb}} + ({u_a} - {u_{0a}})({u_b} - {u_{0b}}))}}\\ \frac{{{f_{xa}}({f_{xb}}{T_{baz}} + ({u_b} - {u_{0b}}){T_{bax}})}}{{{f_{xa}}{f_{xb}} + ({u_a} - {u_{0a}})({u_b} - {u_{0b}})}} \end{array} \right].$ | (5) |
任意空间线段PQ在相机A坐标系中的姿态可以按上述方法在得到点Q在Oa-XaYaZa中的坐标值后确定,也可以根据PQ在Oa-XaYa和Oa-YaZa上投影的方向角确定. 考虑到该模型在长轴类零件位姿检测中的应用特点以及图 1中正交布置的两相机的成像平面o1-x1y1和o2-x2y2分别与Oa-XaYa和Oa-YaZa平行的特性,下面给出由线段PQ分别在o1-x1y1和o2-x2y2上的投影p1q1和p2q2的方向角确定线段PQ姿态的方法.
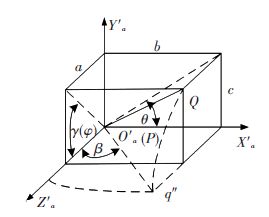
为了分析方便,建立以点P为原点,与坐标系Oa-XaYaZa平行的坐标系$O_{a}^{'}-X_{a}^{'}Y_{a}^{'}Z_{a}^{'}$(如图 2所示). 于是PQ位于坐标系$O_{a}^{'}-X_{a}^{'}Y_{a}^{'}Z_{a}^{'}$中的姿态矩阵$R_{a}^{'}$即为其位于坐标系Oa-XaYaZa中的姿态矩阵Ra. 表示PQ姿态的偏航角β和俯仰角γ可以由PQ在$O_{a}^{'}-X_{a}^{'}Y$平面上的投影与$O_{a}^{'}-X_{a}^{'}$轴的夹角θ和PQ在$O_{a}^{'}-Y_{a}^{'}Z_{a}^{'}$平面上的投影与$O_{a}^{'}-Z_{a}^{'}$轴的夹角φ确定.
|
图 2 计算线段PQ的姿态角原理 Figure 2 Principle of calculating attitude angle of line PQ |
根据如图 1所示的正交双目立体视觉模型,PQ在相机A和相机B图像平面内的投影p1q1和p2q2分别平行于PQ在$O_{a}^{'}-X_{a}^{'}Y_{a}^{'}$和$O_{a}^{'}-Y_{a}^{'}Z_{a}^{'}$上的投影,因此可以通过图像分析求得p1q1与o1-x1轴的夹角θ和p2q2与o2-x2轴的夹角φ,且γ=φ.
同时θ、φ与偏航角β存在如下关系:
| $\begin{align} & \sin ~\beta =\frac{b}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}=\frac{\cos ~\theta }{\sqrt{{{a}^{2}}/\left( {{b}^{2}}+{{c}^{2}} \right)+1}} \\ & \tan ~\varphi =\frac{c}{a}=\frac{\sin ~\theta }{\sqrt{{{a}^{2}}/({{b}^{2}}+{{c}^{2}})}}. \\ \end{align}$ |
消去a、b和c,可得
| $\beta =\arcsin (\cos ~\theta \tan ~\varphi /\sqrt{{{\sin }^{2}}\theta +{{\tan }^{2}}\varphi }).$ | (6) |
于是依据式(6)可以由θ和φ求得β,从而可以确定PQ在Oa-XaYaZa中的姿态矩阵
| ${{R}_{a}}=R_{a}^{'}=Roty\left( \beta \right)Rotx\left( \gamma \right).$ | (7) |
通过对相机外参数标定得到相机A坐标系相对于世界坐标系的位姿变换矩阵Raw和Taw[14-15],便可利用式(5)和式(7)分别求出PQ在世界坐标系中的位置矩阵Tw和姿态矩阵Rw:
| ${{T}_{\text{w}}}={{R}_{a\text{w}}}{{[\begin{matrix} {{X}_{a}} & {{Y}_{a}} & {{Z}_{a}} \\ \end{matrix}]}^{-1}}+{{T}_{a\text{w}}},$ | (8) |
| ${{R}_{\text{w}}}={{R}_{a\text{w}}}{{R}_{a}}.$ | (9) |
轴类零件三维位姿的检测一般可以由以下两种方法实现:1)检测轴类零件的两个端面中心的三维坐标(两个特征点的位置); 2)检测轴类零件其中一个端面中心的三维坐标和其轴线的两个方位角(一个特征点的位置和轴线的姿态).
对于细长型轴类零件,采用第1种方法时,双目相机必须获取包括整个轴两端面的完整图像,对相机的分辨率要求很高. 因此,本文采取第2种方法,即只需双目相机获取轴类零件的一个装配端的部分图像,并且能找到轴线上除端面中心外的另外一点,即可按照前述方法确定其位姿.
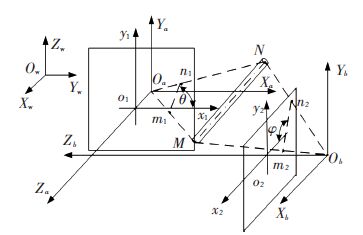
2.1 长轴类零件的空间位置检测方法利用正交双目视觉系统检测轴类零件的原理如图 3所示,其中MN为轴类零件的轴线的一部分(M为装配端中心点,N为轴线上不与M重合的任意一点),MN在相机A和相机B的成像平面上的投影分别为m1n1和m2n2. 以M点作为特征点,对两个相机同时拍摄的端部图像进行阈值分割、特征点提取,便可分别求取特征点M在相机A与相机B的图像坐标系中的位置(ua,va)和(ub,vb),进而利用式(5)和(8)求出点M在世界坐标系Ow-XwYwZw中的空间位置矩阵Tw.
|
图 3 正交双目相机检测轴类零件位姿模型 Figure 3 Model of orthogonal binocular camera for detecting the pose of shaft parts |
对两个相机同时拍摄的长轴类零件装配端的图像进行阈值分割、边缘检测,在相机A和相机B的成像平面内分别求出线段m1n1的方向角θ和m2n2的方向角φ,MN的俯仰角γ=φ,利用式(6)可求出MN的偏航角β,进而利用式(7)和式(9)即可求出长轴类零件装配端的姿态矩阵Rw.
3 实验与结果 3.1 实验系统构建与相机参数标定构建如图 4所示的实验系统,将两个分辨率均为2 592×1 944的CMOS相机A和相机B安装在相机支架上,调整其位置和角度尽量使两光轴正交(保证角度误差<0.1°). 然后将直径为5 mm的短轴(模拟长轴类零件的装配端)通过零件支架安装在精密微动平台上,通过调整微动平台的位置保证特征点M在两相机采集的图像中(各自图像坐标系)的中心区域,并尽量靠近图像的中心. 对两个相机的内参数进行标定,得到两个相机的内参数如表 1所示.

|
图 4 正交双目相机实验系统 Figure 4 Experimental system of orthogonal binocular camera |
| 表 1 相机A和相机B的内参数 Table 1 Internal parameters of camera A and camera B |
通过两个相机拍摄同一块标定板各获得一张图片,可以标定出两个相机的外参数Raw、Taw和R
| ${{R}_{a\text{w}}}=\left[ \begin{matrix} -0.3652 & \text{ }0.8670 & -0.3390 \\ -0.6468 & -0.4982 & -0.5774 \\ -0.6695 & 0.0083 & 0.7427 \\ \end{matrix} \right],$ | (10) |
| ${{T}_{a\text{w}}}=\left[ \begin{matrix} 129.6 \\ 229.4 \\ -284.2 \\ \end{matrix} \right],$ | (11) |
| ${{R}_{b\text{w}}}=\left[ \begin{matrix} -0.3396 & 0.8666 & 0.3655 \\ -0.5773 & -0.4989 & 0.6464 \\ 0.7425 & 0.0085 & 0.6698 \\ \end{matrix} \right],$ | (12) |
| ${{T}_{b\text{w}}}=\left[ \begin{matrix} -71.5 \\ -112.9 \\ -143.7 \\ \end{matrix} \right].$ | (13) |
相机B的相机坐标系相对于相机A的相机坐标系的旋转矩阵Rba和平移矩阵Tba的计算公式为
| $\left[ \begin{matrix} {{R}_{ba}} & {{T}_{ba}} \\ 0 & 1 \\ \end{matrix} \right]={{\left[ \begin{matrix} {{R}_{a\text{w}}} & {{T}_{a\text{w}}} \\ 0 & 1 \\ \end{matrix} \right]}^{-1}}\cdot \left[ \begin{matrix} {{R}_{b\text{w}}} & {{T}_{b\text{w}}} \\ 0 & 1 \\ \end{matrix} \right].$ | (14) |
把式(10)~(13)带入式(14)可得
| ${{R}_{ba}}=\left[ \begin{matrix} 0.0003 & 0.0005 & -1.0000 \\ -0.0006 & 1.0000 & 0.0005 \\ 1.0000 & -0.0007 & 0.0004 \\ \end{matrix} \right],$ | (15) |
| ${{T}_{ba}}=\left[ \begin{align} & {{T}_{bax}} \\ & {{T}_{bay}} \\ & {{T}_{baz}} \\ \end{align} \right]=\left[ \begin{matrix} 200.8 \\ -2.6 \\ 370.2 \\ \end{matrix} \right].$ |
为了验证上述正交双目相机检测长轴类零件装配端三维位姿方法的可行性,调整微动平台使被检测轴类零件的装配端进入到两个相机的视野中心区域,获得如图 5所示两个相机拍摄的装配端的图像. 对两幅图像分别进行处理,利用前述的方法可以得到其装配端端面中心的一组位置(Xw,Yw,Zw)和偏航角β与俯仰角γ. 调整微动平台改变轴类零件的位姿,然后再反向调整微动平台使轴类零件回到调整前的位姿,反复进行5次实验,得到的检测数据如表 2所示.

|
图 5 两个相机检测到的装配端图像 Figure 5 Assembly end images in two cameras |
| 表 2 装配端位姿检测结果 Table 2 Measuring data of assembly end pose |
对表 2中的检测结果进行统计分析,得到如表 3所示的5次检测的平均值、标准差和最大误差. 检测结果相对稳定,含微动平台的误差在内,最大综合位置误差为0.018 mm,最大综合姿态角误差为0.07°. 而文献[12]给出的姿态检测偏差为±1°,位置偏差为±0.2 mm. 实验结果表明,本文给出的正交双目视觉检测轴类零件装配端位姿方法不仅是可行性的,而且位姿检测精度较高.
| 表 3 装配端位姿检测结果统计分析 Table 3 Analysis of measuring data |
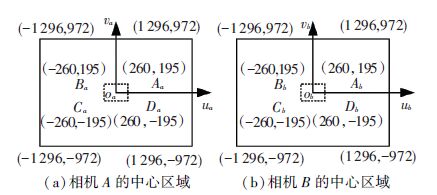
本文实例中两个相机的分辨率均为2 592×1 944,而通过调整微动平台的位置可以保证特征点M在两个图像坐标系中的像素坐标(ua,va)和(ub,vb)均位于(±260,±195)的中心区域内,如图 6所示.
|
图 6 相机图像坐标平面的中心区域 Figure 6 Central area in camera image coordinate systems |
通过(ua,va)和(ub,vb)分别在图 6所示的中心区域内取不同坐标值,按照本文前述的方法分别计算两相机光轴夹角为-90°和-90°±0.1°时特征点M在相机A坐标系中的位置误差,其中误差较大(沿Z轴方向位置)的18组数据如表 4所示.
| 表 4 由相机光轴正交误差所引起的位置误差 Table 4 Position errors by the error of camera axis angle |
由表 4可知,由相机正交误差为0.1°时引起的特征点M的最大测量误差仅为0.021 5 mm(而每个像素在相机坐标空间内代表的实际尺寸为0.023 mm),因此,该误差仅为亚像素级别,可以忽略不计.
另外,比较式(15)和式(4)可知,本实例中经过标定得到的式(15)中Rba的部分元素与由理想正交模型导出的式(4)中Rba的相应元素有微小的偏差,这是由于相机的实际安装位置与理想的正交布置存在-0.012°的正交误差,实例检测时检测到特征点M在相机A和相机B的图像坐标系中的坐标(ua,va)和(ub,vb)分别为(-23,-5) 和(-32,-8). 利用式(4)和式(15)计算出点M在相机A坐标系中的坐标值分别为(-0.549 9,-0.119 5,369.795 0)和 (-0.549 9,-0.119 5,369.794 9). 此实例中由于相机安装误差为0.012°时引起的测量误差为0.000 1 mm,该误差完全可以忽略不计.
由于本文的方法在检测长轴类零件装配端位姿时只需要进行一个特征点的匹配,每次检测计算的时间大约为300 ms,检测速度较快,完全可以应用于基于视觉测量信息实时引导机器人完成精密轴类零件的快速装配中.
4 结 论1) 本文提出的基于正交双目视觉系统检测长轴类零件装配端三维位姿的方法,通过分别检测长轴类零件装配端在两个相机平面内的位置和姿态,然后融合二者信息得到了其三维位姿信息.
2) 该方法有效地克服了非正交双目立体视觉在检测轴类零件位置时需要多个特征点匹配以及难以获取长轴类零件高精度完整图像的弊端,提高了长轴类零件三维位姿的检测速度.
3) 实验结果表明,该方法位置检测精度和姿态检测精度高,检测速度快,能为通过机器视觉引导机器人进行精密轴类零件快速装配及其相关应用提供有力的支持.
| [1] | ZHAO Peng, WANG Nihong. Precise perimeter measurement for 3D object with a binocular stereovision measurement system[J]. Optik-International Journal for Light and Electron Optics, 2009, 121 (10) : 953-957. DOI: 10.1016/j.ijleo.2008.12.008 |
| [2] |
侯宏录, 王敏. 硅棒特征点三维坐标视觉检测技术研究[J].
光学仪器, 2013, 35 (2) : 1-6.
HOU Honglu, WANG min. Study on 3D coordinate detecting technology for characteristic points of silicon rod[J]. Optical Instruments, 2013, 35 (2) : 1-6. DOI: 10.3969/j.issn.1005-5630.2013.02.001 |
| [3] | HUANG Guoshing. 3D coordinate identification of object using binocular vision system for mobile robot[C] //2013 CACS International Automatic Control Conference. Taiwan: IEEE, 2013: 91-96. DOI:10.1109/CACS.2013.6734113. |
| [4] |
夏群峰, 彭勇刚. 基于视觉的机器人抓取系统应用研究综述[J].
机电工程, 2014, 31 (6) : 697-701.
XIA Qunfeng, PENG Yonggang. Review on application research of robots scraping system based on visual[J]. Journal of Mechanical & Electrical Engineering, 2014, 31 (6) : 697-701. DOI: 10.3969/j.issn.1001-4551.2014.06.004 |
| [5] |
李宇飞, 高朝辉, 申麟. 基于视觉的机械臂空间目标抓取策略研究[J].
中国科学技术科学, 2015, 45 (1) : 31-35.
LI Yufei, GAO Chaohui, SHEN Lin. Study of vision-based space target capturing strategy for manipulators[J]. Sci Sin Tech, 2015, 45 (1) : 31-35. DOI: 10.1360/N092014-00320 |
| [6] | XU De, LI Fudong, ZHANG Zhengtao. Characteristic of monocular microscope vision and its application on assembly of micro-pipe and micro-sphere[C]// Proceedings of the 32nd Chinese Control Conference. Xi’an: , 2013: 5758-5763. |
| [7] |
全燕鸣, 黎淑梅, 麦青群. 基于双目视觉的工件尺寸在机三维测量[J].
光学精密工程, 2013, 21 (4) : 1054-1060.
QUAN Yanming, LI Shumei, MAI Qingqun. On-machine 3D measurement of workpiece dimensions based on binocular vision[J]. Optics and Precision Engineering, 2013, 21 (4) : 1054-1060. DOI: 10.3788/OPE.20132104.1054 |
| [8] |
张梁, 徐锦法, 夏青元. 双目立体视觉的无人机位姿估计算法及验证[J].
哈尔滨工业大学学报, 2014, 46 (5) : 66-72.
ZHANG Liang, XU Jinfa, XIA Qingyuan. Pose estimation algorithm and verification based on binocular stereovision for unmanned aerial vehicle[J]. Journal of Harbin Institute of Technology, 2014, 46 (5) : 66-72. |
| [9] | FAN Xinjin, WANG Xuelin, XIAO Yongfei. A shape-based stereo matching algorithm for binocular vision[C]// 2014 IEEE International Conference on Security, Pattern Analysis, and Cybernetics(SPAC). Wuhan: IEEE, 2014: 70-74. DOI:10.1109/SPAC.2014.6982659. |
| [10] |
朱兴龙. 基于立体视觉和激光标记的空间物体位姿的快速定位算法[J].
机械工程学报, 2004, 40 (7) : 161-165.
ZHU Xinglong. Fast localization algorithm for spatial object based on stereo vision and laser marking[J]. Journal of Mechanical Engineering, 2004, 40 (7) : 161-165. DOI: 10.3901/JME.2004.07.161 |
| [11] |
李亮, 赵转萍. 圆筒型热态锻件尺寸的立体视觉测量方法研究[J].
传感器与微系统, 2010, 29 (4) : 49-54.
LI Liang, ZHAO Zhuanping. Study on dimensional measurement of heavy forgoing at high temperature based on binocular stereovision[J]. Transducer and Microsystem Technologies, 2010, 29 (4) : 49-54. DOI: 10.13783/j.1000-9787.2010.04.019 |
| [12] |
李钦杰. 基于激光视觉传感的飞机导管自动装配[D].哈尔滨:哈尔滨工业大学, 2014.
LI Qinjie. Automatic assembly of aircraft pipe based on laser vision sense[D]. Harbin: Harbin Institute of Technology, 2014. |
| [13] |
郭玉波, 姚郁. 双目视觉测量系统结构参数优化问题研究[J].
红外与激光工程, 2006, 35 (z1) : 506-510.
GUO Yubo, YAO Yu. Structural parameter optimization of binocular vision measuring system[J]. Infrared and laser engineering, 2006, 35 (z1) : 506-510. |
| [14] | SONG Weidong, MIAO Zhenjiang,WU Hao. Automatic calibration method based on improved camera calibration template[C]//Wireless, Mobile and Multi-media Networks (ICWMMN 2013). Beijing: ITE, 2013: 301-305. |
| [15] | LI Jia, DUAN Ping. Binocular stereo vision calibration experiment based on essential matrix[C]//Computer and Communication(ICCC).Chengdu: IEEE, 2015: 250-254.DOI:10.1109/Comp-Comm.2015.7387576. |
 2017, Vol. 49
2017, Vol. 49


